DOCSLIB.ORG

Polygons Common Assessment.Pdf

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Polygons Common Assessment.Pdf Math 3 Common Assessment (Revised 2016 SOLs) Polygons SOL 3.12 (a-c) SOL 3.12b 1. Label each polygon with its correct name. A name may be used more than one time. You will not use every name. (Drag and Drop Question. Click and drag the responses to the correct box.) Quadrilateral Hexagon Octagon Pentagon Heptagon Nonagon Decagon SOL 3.12b 2. Which set of figures shows only hexagons? A B C D SOL 3.12b 3. Which figure has less than five vertices? A Hexagon B Rhombus C Pentagon D Octagon SOL 3.12b 4. Which polygon has more than 4 sides and less than 8 sides? A Triangle B Parallelogram C Pentagon D Nonagon SOL 3.12b 5. Read the statements below. Which statement is true? A Heptagons have 3 more sides than quadrilaterals. B A decagon has less sides than a heptagon. C A nonagon has 7 angles. D A pentagon has a greater number of sides than an octagon. SOL 3.12a 6. Identify each picture that represents a polygon. You must select all the correct responses. (IA Note: TEI Hot Spot Item) SOL 3.12a 7. Which of the following is a pentagon? A B C D SOL 3.12a 8. Which of the following has more vertices than a hexagon? A quadrilateral B triangle C pentagon D heptagon SOL 3.12b 9. Which polygon best describes the design below? A Hexagon B Octagon C Heptagon D Pentagon SOL 3.12b 10. What type of polygon has 3 times as many vertices as a triangle? A Decagon B Hexagon C Octagon D Nonagon SOL 3.12b 11. Place the following polygons in order from least to greatest according to the number of vertices. (IA Note: Drag and Drop Question. Click and drag the responses to the correct box.) Least number of ver/ces Decagon Triangle Heptagon Hexagon Greatest number of ver/ces SOL 3.12b 12. Krysta cut a shape out of a piece of construction paper. The shape had 8 sides and 8 angles. Which shape did Krysta make? A Octagon B Heptagon C Decagon D Nonagon SOL 3.12b 13.Jason, Amanda, Megan, and Shane were each asked to name a quadrilateral. Here are their answers: Jason – rectangle Amanda – pentagon Megan – trapezoid Shane - rhombus Who was incorrect? A Jason B Amanda C Megan D Shane SOL 3.12a 14.Which set of figure shows only heptagons? A B C D SOL 3.12b 15. Look at the figure below. The figure can best be described as a(n) – A Decagon because it has ten sides and nine vertices. B Nonagon because it has exactly nine vertices. C Hexagon because it has all congruent sides. D Decagon because it has exactly ten vertices. SOL 3.12c 16.Sarah cut a rectangular piece of paper along the dotted lines shown below. What shapes did she have left? A three triangles and a rectangle B two triangles and a trapezoid C two triangles and a rhombus D two triangles and a parallelogram SOL 3.12c 17.Edward put a puzzle together with the triangular pieces below. What shape did he create? A rectangle B triangle C trapezoid D parallelogram SOL 3.12c 18. Rose combined the shapes below to create a picture of a crayon. What is the name of the polygon she created? A rectangle B hexagon C pentagon D heptagon SOL 3.12c 19. Jonas put three shapes together to create a picture of rocket. What shapes did he use? A triangle, rectangle, trapezoid B triangle, rectangle, rhombus C rectangle, trapezoid, hexagon D square, trapezoid, heptagon.
Load more

Recommended publications
  • PERFORMED IDENTITIES: HEAVY METAL MUSICIANS BETWEEN 1984 and 1991 Bradley C. Klypchak a Dissertation Submitted to the Graduate
    PERFORMED IDENTITIES: HEAVY METAL MUSICIANS BETWEEN 1984 AND 1991 Bradley C. Klypchak A Dissertation Submitted to the Graduate College of Bowling Green State University in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY May 2007 Committee: Dr. Jeffrey A. Brown, Advisor Dr. John Makay Graduate Faculty Representative Dr. Ron E. Shields Dr. Don McQuarie © 2007 Bradley C. Klypchak All Rights Reserved iii ABSTRACT Dr. Jeffrey A. Brown, Advisor Between 1984 and 1991, heavy metal became one of the most publicly popular and commercially successful rock music subgenres. The focus of this dissertation is to explore the following research questions: How did the subculture of heavy metal music between 1984 and 1991 evolve and what meanings can be derived from this ongoing process? How did the contextual circumstances surrounding heavy metal music during this period impact the performative choices exhibited by artists, and from a position of retrospection, what lasting significance does this particular era of heavy metal merit today? A textual analysis of metal- related materials fostered the development of themes relating to the selective choices made and performances enacted by metal artists. These themes were then considered in terms of gender, sexuality, race, and age constructions as well as the ongoing negotiations of the metal artist within multiple performative realms. Occurring at the juncture of art and commerce, heavy metal music is a purposeful construction. Metal musicians made performative choices for serving particular aims, be it fame, wealth, or art. These same individuals worked within a greater system of influence. Metal bands were the contracted employees of record labels whose own corporate aims needed to be recognized.
    [Show full text]
  • Islamic Geometric Ornaments in Istanbul
    ►SKETCH 2 CONSTRUCTIONS OF REGULAR POLYGONS Regular polygons are the base elements for constructing the majority of Islamic geometric ornaments. Of course, in Islamic art there are geometric ornaments that may have different genesis, but those that can be created from regular polygons are the most frequently seen in Istanbul. We can also notice that many of the Islamic geometric ornaments can be recreated using rectangular grids like the ornament in our first example. Sometimes methods using rectangular grids are much simpler than those based or regular polygons. Therefore, we should not omit these methods. However, because methods for constructing geometric ornaments based on regular polygons are the most popular, we will spend relatively more time explor- ing them. Before, we start developing some concrete constructions it would be worthwhile to look into a few issues of a general nature. As we have no- ticed while developing construction of the ornament from the floor in the Sultan Ahmed Mosque, these constructions are not always simple, and in order to create them we need some knowledge of elementary geometry. On the other hand, computer programs for geometry or for computer graphics can give us a number of simpler ways to develop geometric fig- ures. Some of them may not require any knowledge of geometry. For ex- ample, we can create a regular polygon with any number of sides by rotat- ing a point around another point by using rotations 360/n degrees. This is a very simple task if we use a computer program and the only knowledge of geometry we need here is that the full angle is 360 degrees.
    [Show full text]
  • How Can You Put Shapes Together to Make Other Shapes?
    Lesson 27 Understand Tiling in Rectangles Name: How can you put shapes together to make other shapes? Study the example showing how to put shapes together to make other shapes. Then solve Problems 1–4. Example How can you use smaller shapes to make a circle? Look at the shapes in the green box Draw lines to show how you could use the shapes Write how many of each shape you would need 2 4 1 Draw a line to show how you could use squares like the one in the green box to make a rectangle How many squares would you need? squares 2 Draw lines to show how you could use triangles like the one in the green box to make a rectangle How many triangles would you need? triangles ©Curriculum Associates, LLC Copying is not permitted. Lesson 27 Understand Tiling in Rectangles 283 Solve. 3 Draw lines to show how you could use hexagons to make the first shape below Then show how you could use trapezoids to make the second shape How many of each shape would you need? hexagons trapezoids 4 Draw lines to show how you could use triangles to make the first shape below Then show how you could use trapezoids to make the second shape Then show how you could use rhombuses to make the third shape How many of each shape would you need? triangles trapezoids rhombuses 284 Lesson 27 Understand Tiling in Rectangles ©Curriculum Associates, LLC Copying is not permitted. Lesson 27 Name: Draw and Count Squares Study the example showing how to draw and count squares.
    [Show full text]
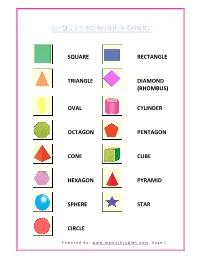
  • Square Rectangle Triangle Diamond (Rhombus) Oval Cylinder Octagon Pentagon Cone Cube Hexagon Pyramid Sphere Star Circle
    SQUARE RECTANGLE TRIANGLE DIAMOND (RHOMBUS) OVAL CYLINDER OCTAGON PENTAGON CONE CUBE HEXAGON PYRAMID SPHERE STAR CIRCLE Powered by: www.mymathtables.com Page 1 what is Rectangle? • A rectangle is a four-sided flat shape where every angle is a right angle (90°). means "right angle" and show equal sides. what is Triangle? • A triangle is a polygon with three edges and three vertices. what is Octagon? • An octagon (eight angles) is an eight-sided polygon or eight-gon. what is Hexagon? • a hexagon is a six-sided polygon or six-gon. The total of the internal angles of any hexagon is 720°. what is Pentagon? • a plane figure with five straight sides and five angles. what is Square? • a plane figure with four equal straight sides and four right angles. • every angle is a right angle (90°) means "right ang le" show equal sides. what is Rhombus? • is a flat shape with four equal straight sides. A rhombus looks like a diamond. All sides have equal length. Opposite sides are parallel, and opposite angles are equal what is Oval? • Many distinct curves are commonly called ovals or are said to have an "oval shape". • Generally, to be called an oval, a plane curve should resemble the outline of an egg or an ellipse. Powered by: www.mymathtables.com Page 2 What is Cube? • Six equal square faces.tweleve edges and eight vertices • the angle between two adjacent faces is ninety. what is Sphere? • no faces,sides,vertices • All points are located at the same distance from the center. what is Cylinder? • two circular faces that are congruent and parallel • faces connected by a curved surface.
    [Show full text]
  • Geometry Honors Mid-Year Exam Terms and Definitions Blue Class 1
    Geometry Honors Mid-Year Exam Terms and Definitions Blue Class 1. Acute angle: Angle whose measure is greater than 0° and less than 90°. 2. Adjacent angles: Two angles that have a common side and a common vertex. 3. Alternate interior angles: A pair of angles in the interior of a figure formed by two lines and a transversal, lying on alternate sides of the transversal and having different vertices. 4. Altitude: Perpendicular segment from a vertex of a triangle to the opposite side or the line containing the opposite side. 5. Angle: A figure formed by two rays with a common endpoint. 6. Angle bisector: Ray that divides an angle into two congruent angles and bisects the angle. 7. Base Angles: Two angles not included in the legs of an isosceles triangle. 8. Bisect: To divide a segment or an angle into two congruent parts. 9. Coincide: To lie on top of the other. A line can coincide another line. 10. Collinear: Lying on the same line. 11. Complimentary: Two angle’s whose sum is 90°. 12. Concave Polygon: Polygon in which at least one interior angle measures more than 180° (at least one segment connecting two vertices is outside the polygon). 13. Conclusion: A result of summary of all the work that has been completed. The part of a conditional statement that occurs after the word “then”. 14. Congruent parts: Two or more parts that only have the same measure. In CPCTC, the parts of the congruent triangles are congruent. 15. Congruent triangles: Two triangles are congruent if and only if all of their corresponding parts are congruent.
    [Show full text]
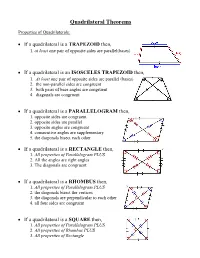
  • Quadrilateral Theorems
    Quadrilateral Theorems Properties of Quadrilaterals: If a quadrilateral is a TRAPEZOID then, 1. at least one pair of opposite sides are parallel(bases) If a quadrilateral is an ISOSCELES TRAPEZOID then, 1. At least one pair of opposite sides are parallel (bases) 2. the non-parallel sides are congruent 3. both pairs of base angles are congruent 4. diagonals are congruent If a quadrilateral is a PARALLELOGRAM then, 1. opposite sides are congruent 2. opposite sides are parallel 3. opposite angles are congruent 4. consecutive angles are supplementary 5. the diagonals bisect each other If a quadrilateral is a RECTANGLE then, 1. All properties of Parallelogram PLUS 2. All the angles are right angles 3. The diagonals are congruent If a quadrilateral is a RHOMBUS then, 1. All properties of Parallelogram PLUS 2. the diagonals bisect the vertices 3. the diagonals are perpendicular to each other 4. all four sides are congruent If a quadrilateral is a SQUARE then, 1. All properties of Parallelogram PLUS 2. All properties of Rhombus PLUS 3. All properties of Rectangle Proving a Trapezoid: If a QUADRILATERAL has at least one pair of parallel sides, then it is a trapezoid. Proving an Isosceles Trapezoid: 1st prove it’s a TRAPEZOID If a TRAPEZOID has ____(insert choice from below) ______then it is an isosceles trapezoid. 1. congruent non-parallel sides 2. congruent diagonals 3. congruent base angles Proving a Parallelogram: If a quadrilateral has ____(insert choice from below) ______then it is a parallelogram. 1. both pairs of opposite sides parallel 2. both pairs of opposite sides ≅ 3.
    [Show full text]
  • Framing Cyclic Revolutionary Emergence of Opposing Symbols of Identity Eppur Si Muove: Biomimetic Embedding of N-Tuple Helices in Spherical Polyhedra - /
    Alternative view of segmented documents via Kairos 23 October 2017 | Draft Framing Cyclic Revolutionary Emergence of Opposing Symbols of Identity Eppur si muove: Biomimetic embedding of N-tuple helices in spherical polyhedra - / - Introduction Symbolic stars vs Strategic pillars; Polyhedra vs Helices; Logic vs Comprehension? Dynamic bonding patterns in n-tuple helices engendering n-fold rotating symbols Embedding the triple helix in a spherical octahedron Embedding the quadruple helix in a spherical cube Embedding the quintuple helix in a spherical dodecahedron and a Pentagramma Mirificum Embedding six-fold, eight-fold and ten-fold helices in appropriately encircled polyhedra Embedding twelve-fold, eleven-fold, nine-fold and seven-fold helices in appropriately encircled polyhedra Neglected recognition of logical patterns -- especially of opposition Dynamic relationship between polyhedra engendered by circles -- variously implying forms of unity Symbol rotation as dynamic essential to engaging with value-inversion References Introduction The contrast to the geocentric model of the solar system was framed by the Italian mathematician, physicist and philosopher Galileo Galilei (1564-1642). His much-cited phrase, " And yet it moves" (E pur si muove or Eppur si muove) was allegedly pronounced in 1633 when he was forced to recant his claims that the Earth moves around the immovable Sun rather than the converse -- known as the Galileo affair. Such a shift in perspective might usefully inspire the recognition that the stasis attributed so widely to logos and other much-valued cultural and heraldic symbols obscures the manner in which they imply a fundamental cognitive dynamic. Cultural symbols fundamental to the identity of a group might then be understood as variously moving and transforming in ways which currently elude comprehension.
    [Show full text]
  • Applying the Polygon Angle
    POLYGONS 8.1.1 – 8.1.5 After studying triangles and quadrilaterals, students now extend their study to all polygons. A polygon is a closed, two-dimensional figure made of three or more non- intersecting straight line segments connected end-to-end. Using the fact that the sum of the measures of the angles in a triangle is 180°, students learn a method to determine the sum of the measures of the interior angles of any polygon. Next they explore the sum of the measures of the exterior angles of a polygon. Finally they use the information about the angles of polygons along with their Triangle Toolkits to find the areas of regular polygons. See the Math Notes boxes in Lessons 8.1.1, 8.1.5, and 8.3.1. Example 1 4x + 7 3x + 1 x + 1 The figure at right is a hexagon. What is the sum of the measures of the interior angles of a hexagon? Explain how you know. Then write an equation and solve for x. 2x 3x – 5 5x – 4 One way to find the sum of the interior angles of the 9 hexagon is to divide the figure into triangles. There are 11 several different ways to do this, but keep in mind that we 8 are trying to add the interior angles at the vertices. One 6 12 way to divide the hexagon into triangles is to draw in all of 10 the diagonals from a single vertex, as shown at right. 7 Doing this forms four triangles, each with angle measures 5 4 3 1 summing to 180°.
    [Show full text]
  • Polygon Review and Puzzlers in the Above, Those Are Names to the Polygons: Fill in the Blank Parts. Names: Number of Sides
    Polygon review and puzzlers ÆReview to the classification of polygons: Is it a Polygon? Polygons are 2-dimensional shapes. They are made of straight lines, and the shape is "closed" (all the lines connect up). Polygon Not a Polygon Not a Polygon (straight sides) (has a curve) (open, not closed) Regular polygons have equal length sides and equal interior angles. Polygons are named according to their number of sides. Name of Degree of Degree of triangle total angles regular angles Triangle 180 60 In the above, those are names to the polygons: Quadrilateral 360 90 fill in the blank parts. Pentagon Hexagon Heptagon 900 129 Names: number of sides: Octagon Nonagon hendecagon, 11 dodecagon, _____________ Decagon 1440 144 tetradecagon, 13 hexadecagon, 15 Do you see a pattern in the calculation of the heptadecagon, _____________ total degree of angles of the polygon? octadecagon, _____________ --- (n -2) x 180° enneadecagon, _____________ icosagon 20 pentadecagon, _____________ These summation of angles rules, also apply to the irregular polygons, try it out yourself !!! A point where two or more straight lines meet. Corner. Example: a corner of a polygon (2D) or of a polyhedron (3D) as shown. The plural of vertex is "vertices” Test them out yourself, by drawing diagonals on the polygons. Here are some fun polygon riddles; could you come up with the answer? Geometry polygon riddles I: My first is in shape and also in space; My second is in line and also in place; My third is in point and also in line; My fourth in operation but not in sign; My fifth is in angle but not in degree; My sixth is in glide but not symmetry; Geometry polygon riddles II: I am a polygon all my angles have the same measure all my five sides have the same measure, what general shape am I? Geometry polygon riddles III: I am a polygon.
    [Show full text]
  • Properties of N-Sided Regular Polygons
    PROPERTIES OF N-SIDED REGULAR POLYGONS When students are first exposed to regular polygons in middle school, they learn their properties by looking at individual examples such as the equilateral triangles(n=3), squares(n=4), and hexagons(n=6). A generalization is usually not given, although it would be straight forward to do so with just a min imum of trigonometry and algebra. It also would help students by showing how one obtains generalization in mathematics. We show here how to carry out such a generalization for regular polynomials of side length s. Our starting point is the following schematic of an n sided polygon- We see from the figure that any regular n sided polygon can be constructed by looking at n isosceles triangles whose base angles are θ=(1-2/n)(π/2) since the vertex angle of the triangle is just ψ=2π/n, when expressed in radians. The area of the grey triangle in the above figure is- 2 2 ATr=sh/2=(s/2) tan(θ)=(s/2) tan[(1-2/n)(π/2)] so that the total area of any n sided regular convex polygon will be nATr, , with s again being the side-length. With this generalized form we can construct the following table for some of the better known regular polygons- Name Number of Base Angle, Non-Dimensional 2 sides, n θ=(π/2)(1-2/n) Area, 4nATr/s =tan(θ) Triangle 3 π/6=30º 1/sqrt(3) Square 4 π/4=45º 1 Pentagon 5 3π/10=54º sqrt(15+20φ) Hexagon 6 π/3=60º sqrt(3) Octagon 8 3π/8=67.5º 1+sqrt(2) Decagon 10 2π/5=72º 10sqrt(3+4φ) Dodecagon 12 5π/12=75º 144[2+sqrt(3)] Icosagon 20 9π/20=81º 20[2φ+sqrt(3+4φ)] Here φ=[1+sqrt(5)]/2=1.618033989… is the well known Golden Ratio.
    [Show full text]
  • Interior and Exterior Angles of Polygons 2A
    Regents Exam Questions Name: ________________________ G.CO.C.11: Interior and Exterior Angles of Polygons 2a www.jmap.org G.CO.C.11: Interior and Exterior Angles of Polygons 2a 1 Which type of figure is shown in the accompanying 5 In the diagram below of regular pentagon ABCDE, diagram? EB is drawn. 1) hexagon 2) octagon 3) pentagon 4) quadrilateral What is the measure of ∠AEB? 2 What is the measure of each interior angle of a 1) 36º regular hexagon? 2) 54º 1) 60° 3) 72º 2) 120° 4) 108º 3) 135° 4) 270° 6 What is the measure, in degrees, of each exterior angle of a regular hexagon? 3 Determine, in degrees, the measure of each interior 1) 45 angle of a regular octagon. 2) 60 3) 120 4) 135 4 Determine and state the measure, in degrees, of an interior angle of a regular decagon. 7 A stop sign in the shape of a regular octagon is resting on a brick wall, as shown in the accompanying diagram. What is the measure of angle x? 1) 45° 2) 60° 3) 120° 4) 135° 1 Regents Exam Questions Name: ________________________ G.CO.C.11: Interior and Exterior Angles of Polygons 2a www.jmap.org 8 One piece of the birdhouse that Natalie is building 12 The measure of an interior angle of a regular is shaped like a regular pentagon, as shown in the polygon is 120°. How many sides does the polygon accompanying diagram. have? 1) 5 2) 6 3) 3 4) 4 13 Melissa is walking around the outside of a building that is in the shape of a regular polygon.
    [Show full text]
  • The Other Tchaikowsky
    The Other Tchaikowsky A biographical sketch of André Tchaikowsky David A. Ferré Cover painting: André Tchaikowsky courtesy of Milein Cosman (Photograph by Ken Grundy) About the cover The portrait of André Tchaikowsky at the keyboard was painted by Milein Cosman (Mrs. Hans Keller) in 1975. André had come to her home for a visit for the first time after growing a beard. She immediately suggested a portrait be made. It was completed in two hours, in a single sitting. When viewing the finished picture, André said "I'd love to look like that, but can it possibly be me?" Contents Preface Chapter 1 - The Legacy (1935-1982) Chapter 2 - The Beginning (1935-1939) Chapter 3 - Survival (1939-1945 Chapter 4 - Years of 'Training (1945-1957) Chapter 5 - A Career of Sorts (1957-1960) Chapter 6 - Homeless in London (1960-1966) Chapter 7 - The Hampstead Years (1966-1976) Chapter 8 - The Cumnor Years (1976-1982) Chapter 9 - Quodlibet Acknowledgments List of Compositions List of Recordings i Copyright 1991 and 2008 by David A. Ferré David A. Ferré 2238 Cozy Nook Road Chewelah, WA 99109 USA [email protected] http://AndreTchaikowsky.com Preface As I maneuvered my automobile through the dense Chelsea traffic, I noticed that my passenger had become strangely silent. When I sneaked a glance I saw that his eyes had narrowed and he held his mouth slightly open, as if ready to speak but unable to bring out the words. Finally, he managed a weak, "Would you say that again?" It was April 1985, and I had just arrived in London to enjoy six months of vacation and to fulfill an overdue promise to myself.
    [Show full text]