A Conceptual Model of Irrigation Development B Source Materials
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

8144 Yanco Agricultural High School Annual School Report 2014
Yanco Agricultural High School Annual School Report 2014 8144 School context statement Year 12 student Lily Serafin received a John Yanco Agricultural High School is a co- Lincoln Youth Community Service Award from the educational, fully residential high school, Governor, Professor The Honourable Dame Marie specialising in Agriculture. The school provides a Bashir AD CVO quality secondary education in a historic rural 2014 saw the evaluation of the highly successful setting. middle school concept with students in Years 7 Located in the NSW Riverina the school has a and 8 undertaking a curriculum program with proud tradition of promoting positive values and combined subject outcomes, the number of developing confident, capable, community- teachers reduced by teaching combined subjects, minded students. The school is a selective home room identification (Year 7) and an government school with priority given to isolated improved orientation program in their early students. months in the residential school. Improved This unique educational institution provides a coordination of the curriculum across the school broad, well balanced education. The school has has commenced during the year. In 2015 the Year 280 hectares, including 180ha of intensive 7 classes will remain single sex with the Year 8 irrigation and dry land agriculture, as well as 60 classes being streamed to meet the needs of the hectares of natural bushland bordered by the students in this cohort. Murrumbidgee River. With state-of-the-art trade training resources, The transition program which was established in farm and hostel, the school provides an all-round 2009 for students entering Year 7 continues to education for students in a stimulating and caring flourish and is integral for the orientation of both environment. -

Greater Hume Shire Visitor Experience Plan 2014 - 2018 Contact
GREATER HUME SHIRE VISITOR EXPERIENCE PLAN 2014 - 2018 Contact: Kerrie Wise, Tourism and Promotions Officer [email protected] 02 6036 0186 0448 099 536 PO Box 99, 39 Young Street HOLBROOK NSW 2644 © Copyright, Greater Hume Shire Council, December 2013. This work is copyright. Apart from any use as permitted under Copyright Act 1963, no part may be reproduced without written permission of the Greater Hume Shire Council. Document Information ECO.STRAT.0001.002 Last Saved December 2013 Last Printed December 2013 File Size 1189kb Disclaimer Neither Greater Hume Shire Council nor any member or employee of Greater Hume Shire Council takes responsibility in any way whatsoever to any person or organisation (other than that for which this report has been prepared) in respect of the information set out in this report, including any errors or omissions therein. In the course of our preparation of this report, projections have been prepared on the basis of assumptions and methodology which have been described in the report. It is possible that some of the assumptions underlying the projections may change. Nevertheless, the professional judgement of the members and employees of Greater Hume Shire Council have been applied in making these assumptions, such that they constitute an understandable basis for estimates and projections. Beyond this, to the extent that the assumptions do not materialise, the estimates and projections of achievable results may vary. Greater Hume Shire Council – Visitor Experience Plan - 2014 - 2018 2 ECO.STRAT.0001.002 -

Roads Thematic History
Roads and Maritime Services Roads Thematic History THIS PAGE LEFT INTENTIONALLY BLANK ROADS AND TRAFFIC AUTHORITY HERITAGE AND CONSERVATION REGISTER Thematic History Second Edition, 2006 RTA Heritage and Conservation Register – Thematic History – Second Edition 2006 ____________________________________________________________________________________ ROADS AND TRAFFIC AUTHORITY HERITAGE AND CONSERVATION REGISTER Thematic History Second Edition, 2006 Compiled for the Roads and Traffic Authority as the basis for its Heritage and Conservation (Section 170) Register Terry Kass Historian and Heritage Consultant 32 Jellicoe Street Lidcombe NSW, 2141 (02) 9749 4128 February 2006 ____________________________________________________________________________________ 2 RTA Heritage and Conservation Register – Thematic History – Second Edition 2006 ____________________________________________________________________________________ Cover illustration: Peak hour at Newcastle in 1945. Workers cycling to work join the main Maitland Road at the corner of Ferndale Street. Source: GPO1, ML, 36269 ____________________________________________________________________________________ 3 RTA Heritage and Conservation Register – Thematic History – Second Edition 2006 ____________________________________________________________________________________ Abbreviations DMR Department of Main Roads, 1932-89 DMT Department of Motor Transport, 1952-89 GPO1 Government Printer Photo Collection 1, Mitchell Library MRB Main Roads Board, 1925-32 SRNSW State Records of New South -

NSW Police Gazette 1878
This sampler file contains various sample pages from the product. Sample pages will often include: the title page, an index, and other pages of interest. This sample is fully searchable (read Search Tips) but is not FASTFIND enabled. To view more samplers click here www.gould.com.au www.archivecdbooks.com.au · The widest range of Australian, English, · Over 1600 rare Australian and New Zealand Irish, Scottish and European resources books on fully searchable CD-ROM · 11000 products to help with your research · Over 3000 worldwide · A complete range of Genealogy software · Including: Government and Police 5000 data CDs from numerous countries gazettes, Electoral Rolls, Post Office and Specialist Directories, War records, Regional Subscribe to our weekly email newsletter histories etc. FOLLOW US ON TWITTER AND FACEBOOK www.unlockthepast.com.au · Promoting History, Genealogy and Heritage in Australia and New Zealand · A major events resource · regional and major roadshows, seminars, conferences, expos · A major go-to site for resources www.familyphotobook.com.au · free information and content, www.worldvitalrecords.com.au newsletters and blogs, speaker · Free software download to create biographies, topic details · 50 million Australasian records professional looking personal photo books, · Includes a team of expert speakers, writers, · 1 billion records world wide calendars and more organisations and commercial partners · low subscriptions · FREE content daily and some permanently This sampler file includes the title page and various sample pages from this volume. This file is fully searchable (read search tips page) but is not FASTFIND enabled New South Wales Police Gazette 1878 Ref. AU2103-1878 ISBN: 978 1 921416 10 1 This book was kindly loaned to Archive CD Books Australia by New South Wales Justice and Police Museum http://www.hht.net.au/museums/jp/justice_and_police_museum Navigating this CD To view the contents of this CD use the bookmarks and Adobe Reader’s forward and back buttons to browse through the pages. -

Infrastructure Statement 2020-21 – NSW Budget Paper No. 3
Infrastructure Statement 2020-21 Budget Paper No. 3 Circulated by The Hon. Dominic Perrottet MP, Treasurer TABLE OF CONTENTS Chart, Figure and Table List Focus Box List About this Budget Paper ........................................................................................... i Chapter 1: Overview 1.1 Adapting the State’s infrastructure program ........................................... 1 - 2 1.2 Infrastructure generating jobs and economic activity .............................. 1 - 7 1.3 Our fiscal management ........................................................................... 1 - 9 1.4 Four-year capital program ........................................................................ 1 - 10 1.5 Funding the delivery of infrastructure ...................................................... 1 - 12 1.6 Existing assets and maintenance program ............................................. 1 - 14 1.7 Infrastructure Investment Assurance ........................................................ 1 - 16 Chapter 2: Delivering Our Job Creating Infrastructure Pipeline 2.1 Key infrastructure projects delivered since the 2019-20 Budget ............ 2 - 2 2.2 Key infrastructure projects in delivery ..................................................... 2 - 8 2.3 Digital delivery ......................................................................................... 2 - 31 Chapter 3: The Restart NSW Fund 3.1 Overview ................................................................................................. 3 - 1 3.2 Restart NSW commitments -

Drownings in Albury and District
ALBURY-WODONGA DROWNINGS IN AND AROUND THE MURRAY RIVER & LAKE HUME This list has been compiled by Howard Jones, Greg Ryan and Helen Livsey from the Border Mail and other contemporary newspaper reports, the Albury & Border Rescue Squad (Mr Peter Adams), the register of NSW Coroners’ Inquests to 1937 (at https://www.ancestry.com.au/), the Albury Cemeteries on-line facility, and records kept by the Albury & District Historical Society. Because of gaps in records, it is probable that are several omissions from the list. Anyone who can add to it should contact the Society – contact details at https://alburyhistory.org.au/contact/. Updated October 26, 2019 1846 An early Albury medical practitioner drowned in the Murray at the Crossing Place (Dr Ward). 1854 (October): A young woman, 19, and a youth, were returning from the Bonegilla station to Table Top when the log punt or canoe they were in sank. Both drowned (Huon & Mitchell). 1855 (January): Two boys, sons of a Wodonga publican and a pub employee, drowned when they bathed in a lagoon near the river (Barnes and unknown). 1856 (January): A bandsman (unnamed) who had played at a public dinner on New Year’s Day honouring paddlesteamer captain Francis Cadell went to bathe in the river and drowned. (September): A mailman, 46, drowned when he tried to ride his horse across the flooded Murray. The mail bags were recovered (Lowe). 1857 (February): A young man was swimming with mates at the Mitta/Murray junction when he was seized by cramp, and failed to reach the bank despite being a good swimmer. -
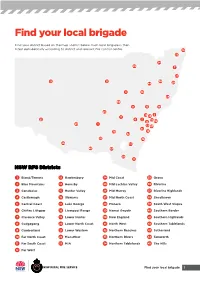
Find Your Local Brigade
Find your local brigade Find your district based on the map and list below. Each local brigade is then listed alphabetically according to district and relevant fire control centre. 10 33 34 29 7 27 12 31 30 44 20 4 18 24 35 8 15 19 25 13 5 3 45 21 6 2 14 9 32 23 1 22 43 41 39 16 42 36 38 26 17 40 37 28 11 NSW RFS Districts 1 Bland/Temora 13 Hawkesbury 24 Mid Coast 35 Orana 2 Blue Mountains 14 Hornsby 25 Mid Lachlan Valley 36 Riverina 3 Canobolas 15 Hunter Valley 26 Mid Murray 37 Riverina Highlands 4 Castlereagh 16 Illawarra 27 Mid North Coast 38 Shoalhaven 5 Central Coast 17 Lake George 28 Monaro 39 South West Slopes 6 Chifley Lithgow 18 Liverpool Range 29 Namoi Gwydir 40 Southern Border 7 Clarence Valley 19 Lower Hunter 30 New England 41 Southern Highlands 8 Cudgegong 20 Lower North Coast 31 North West 42 Southern Tablelands 9 Cumberland 21 Lower Western 32 Northern Beaches 43 Sutherland 10 Far North Coast 22 Macarthur 33 Northern Rivers 44 Tamworth 11 Far South Coast 23 MIA 34 Northern Tablelands 45 The Hills 12 Far West Find your local brigade 1 Find your local brigade 1 Bland/Temora Springdale Kings Plains – Blayney Tara – Bectric Lyndhurst – Blayney Bland FCC Thanowring Mandurama Alleena Millthorpe Back Creek – Bland 2 Blue Mountains Neville Barmedman Blue Mountains FCC Newbridge Bland Creek Bell Panuara – Burnt Yards Blow Clear – Wamboyne Blackheath / Mt Victoria Tallwood Calleen – Girral Blaxland Cabonne FCD Clear Ridge Blue Mtns Group Support Baldry Gubbata Bullaburra Bocobra Kikiora-Anona Faulconbridge Boomey Kildary Glenbrook -

Rethinking Cement Support Our Work
Zero Carbon Australia Presents Zero Carbon Industry Plan Rethinking Cement Support our work Beyond Zero Emissions is one of Australia’s most respected climate change think tanks. We produce independent research demonstrating that zero emissions is achievable and affordable now. Our work is carried out by a small staff of experts, with the help of academic institutions and a large network of volunteer scientists, engineers and economists. We are funded by private foundations and concerned individuals. You can be a part of our audacious vision for a Zero Carbon Australia by making a donation to fund our research. Eighty- five per cent of our researchers are volunteers, making your donation go a long way. To find out how visit: http://bze.org.au Published by Beyond Zero Emissions Inc. Kindness House Suite 16, Level 1 288 Brunswick Street Fitzroy, Victoria 3065 First published August 2017 Zero Carbon Industry Plan: Rethinking Cement should be attributed to Beyond Zero Emissions. This publication is licensed under the Creative Commons Attribution 3.0 Australia License. In essence, you are free to copy, distribute and adapt the work, as long as you attribute the work and abide by the other license terms. To view a copy of this licence, visit: https://creativecommons.org/licenses/by-nc-sa/3.0 This document is available for download from http://bze.org.au Requests and inquiries should be directed to [email protected] ISBN: 978-0-9923580-2-0 This document is printed with Monza Recycled Digital contains 99% recycled fibre and is FSC® Mix certified pulp, which ensures all virgin pulp is derived from well-managed forests and controlled sources. -

John Marinovich Director
John Marinovich Director Areas of Expertise Planning, Programming, Project Management, Dispute Resolution Industries Infrastructure, Roads, Resource & Mining, ICT Qualifications Bachelor of Applied Science (Building) Post Graduate Diploma Project Management Accredited Expert Witness (RICS) Certificate in SOPA Adjudication (NSW) Key Experiences John joined TBH as a consultant in 1989 and has been a Director since 2004. He has over 30 years’ experience in the construction and infrastructure industries, with a particular emphasis on project delivery and planning advice, contractual claims and dispute advice. John has been responsible for providing advice on project strategies, time management of design, procurement, construction and commissioning, contract management, risk management, value management and the preparation and, or defence of contractual claims. John has worked on several major capital works program projects, undertaking the role of project co-ordinator throughout the design, documentation, tender, construction and commissioning phases. Prior to joining TBH, John worked for developers and building companies with on-site and office positions and gained experience in contract administration, estimating, tender preparation and project planning. A Director of TBH since 2004, John has been responsible for providing advice on the project delivery strategies and control of time on numerous projects. John Marinovich | tbhconsultancy.com John’s work at TBH includes: Project Management Advice • Providing advice to various clients (public -

Albury District Technical Manual III
- I APRIL, 1978 II CONTENTS 1 INTRODUCTION R.S.Junor 1.1 Boundaries 1.2 Local Government Administration 1.3 Historical Development 2 GEOLOGY R.S. Junor 2.1 Introduction 2.2 Description of Geological Units 2.3 Relationship of Geology to Erosion 3 LANDFORM C.M. Adamson 3.1 Introduction 3.2 Description of Landform Classes 4 CLIMATE W.H.Johnston 4.1 Introduction 4.2 Rainfall 4.3 Temperature 4.4 Evaporation 4.5 Climate and Plant Growth 4.6 Interrelationships of Factors 4.7 Climate and Soil Conservation 5 SOILS R.J. Crouch 5.1 The Soils Map 5.2 Major Soil Associations 5.3 Soil Toposequences 5.4 A Guide to Soil Codings 5.5 Soil Properties and Design Criteria 5.6 Soil Testing and Procedures 6 VEGETATION W.H. Johnston 6.1 Introduction 6.2 Study Objectives 6.3 Plant Communities and structural Organization 6.4 Wet Sclerophyll Forest Formation 6.5 Intermediate Sclerophyll Forest Formation 6.6 Dry Selerophyll Forest Formation 6.7 Tall Woodland Formation 6.8 Savannah Woodland Formation 6.9 Understory Vegetation 6.10 Factors affecting the distribution of vegetation 6.11 Vegetation and Land Use 6.12 Vegetation and Erosion Soil Conservation Service of N.S.W. - Albury District Technical Manual III 7 LAND USE R.J.Crouch 7.1 Introduction 7.2 Landuse Units 7.3 Farm Size and Landuse 7.4 Landuse potential and possible trends 8 EROSION C.M. Adamson 8.1 General 8.2 The Erosion Map 8.3 No appreciable erosion 8.4 sheet Erosion 8.5 Gully Erosion 9 GENERAL SOIL CONSERVATION PRACTICES R.S. -

Cumberland /Prospect DDS 4 AGEING, DISABILITY and HOME
METROPOLITAN CONSTITUENCY DELEGATES AGEING, DISABILITY AND HOME CARE – Cumberland /Prospect DDS 4 AGEING, DISABILITY AND HOME CARE – Hornsby-Ryde DDS 2 AGEING, DISABILITY AND HOME CARE – Inner West DDS 2 AGEING, DISABILITY AND HOME CARE – Manly-St. Leonards DDS 1 AGEING, DISABILITY AND HOME CARE – Nepean DDS 2 AGEING, DISABILITY AND HOME CARE – South East/St. George DDS 1 AGEING, DISABILITY AND HOME CARE – South Western DDS 1 (AGEING, DISABILITY AND HOME CARE - Department of (AGEING, DISABILITY AND HOME CARE – South Eastern DDS (HOME CARE SERVICE NSW – Metropolitan 2 AUSTRALIAN MUSEUM 1 AUDIT OFFICE OF NSW, THE - *See Combined Met. East (AUSTRALIAN CATHOLIC UNIVERSITY (MACQUARIE UNIVERSITY 1 BOARD OF STUDIES, TEACHING & EDUCATIONAL STANDARDS NSW - *See Combined Met. East BOTANIC GARDENS & DOMAIN TRUST, THE ROYAL – Metropolitan 1 (COMBINED – METROPOLITAN EAST* (ART GALLERY OF NSW (AUDIT OFFICE OF NSW (BOARD OF STUDIES,TEACHING & EDUCATIONAL STANDARDS NSW (COMMUNITY RELATIONS COMMISSION (INDUSTRIAL RELATIONS COMMISSION OF NSW – Head Office (LIQUOR, GAMING & RACING, NSW OFFICE OF (LOCAL GOVERNMENT, OFFICE OF (OMBUDSMAN NSW (PARK TRUSTS – Metropolitan (incl Centennial Park/West. Syd/Parra) (SPORT & RECREATION TARONGA CONSERVATION SOCIETY AUSTRALIA (TRADE & INVESTMENT, REGIONAL INFRASTRUCTURE & SERVICES (TRANSGRID – Metropolitan (WOMEN NSW 14 (COMBINED –METROPOLITAN WEST* (ARTS NSW – Metropolitan General (INDUSTRIAL RELATIONS COMMISSION OF NSW – Metropolitan General 5 COMMUNITY SERVICES – Cumberland /Prospect 4 COMMUNITY SERVICES – Nepean -

South West Slopes Revegetation Guide
ot etSoe Rvgtto Guide South West Slopes Revegetation ot etSoe Rvgtto Guide South West Slopes Revegetation from little things big things grow... SouthSouth WestWest SlopesSlopes RevegetationRevegetation GuideGuide (south of the Murrumbidgee River) 1998 from little things big things grow... South West Slopes Revegetation Guide (SOUTH OF THE MURRUMBIDGEE RIVER) Edited by Fleur Stelling Murray Catchment Management Committee & Department of Land & Water Conservation Albury, NSW March 1998. With a major contribution by Karen Walker Greening Australia, Wagga Wagga, NSW. foreword John Landy he South West Slopes region of New South introduced species of plants and animals and grazing T Wales runs from the Riverina plains to the have all played a part in the decline in biodiversity of mountains in the east, with an elevation of up to native vegetation. This book provides useful material 600 metres. It is one of the most extensively altered for those seeking to control weeds, attract wildlife to landscapes in this country. The most radical the farm dam, or reintroduce native grasses and modification has been on the lower slopes and plains, pasture. The practical information sheets will also be where the establishment of pastures and crops was valuable in many aspects of land management. most easily achieved. Clearing of the catchments in the rising country, mainly during the last century — has Many farmers in the South West Slopes region (and resulted in eroded streams and silt deposition, the latter elsewhere in the country) have struggled under encouraged by the widespread growing of willows. increasingly adverse conditions. My family has a property in the south-east, near Tooma, and we have Preserving the remaining areas of bushland that have had to step up our fight against weeds (notably the so far escaped a significant decline in biodiversity is blackberry), which infests pasture and modified clearly a priority, and several chapters in this Guide bushland alike.