Estimation of Exhaust Manifold Pressure in Turbocharged Gasoline Engines with Variable Valve Timing
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Mean Value Modelling of a Poppet Valve EGR-System
Mean value modelling of a poppet valve EGR-system Master’s thesis performed in Vehicular Systems by Claes Ericson Reg nr: LiTH-ISY-EX-3543-2004 14th June 2004 Mean value modelling of a poppet valve EGR-system Master’s thesis performed in Vehicular Systems, Dept. of Electrical Engineering at Linkopings¨ universitet by Claes Ericson Reg nr: LiTH-ISY-EX-3543-2004 Supervisor: Jesper Ritzen,´ M.Sc. Scania CV AB Mattias Nyberg, Ph.D. Scania CV AB Johan Wahlstrom,¨ M.Sc. Linkopings¨ universitet Examiner: Associate Professor Lars Eriksson Linkopings¨ universitet Linkoping,¨ 14th June 2004 Avdelning, Institution Datum Division, Department Date Vehicular Systems, Dept. of Electrical Engineering 14th June 2004 581 83 Linkoping¨ Sprak˚ Rapporttyp ISBN Language Report category — ¤ Svenska/Swedish ¤ Licentiatavhandling ISRN ¤ Engelska/English ££ ¤ Examensarbete LITH-ISY-EX-3543-2004 ¤ C-uppsats Serietitel och serienummer ISSN ¤ D-uppsats Title of series, numbering — ¤ ¤ Ovrig¨ rapport ¤ URL for¨ elektronisk version http://www.vehicular.isy.liu.se http://www.ep.liu.se/exjobb/isy/2004/3543/ Titel Medelvardesmodellering¨ av EGR-system med tallriksventil Title Mean value modelling of a poppet valve EGR-system Forfattare¨ Claes Ericson Author Sammanfattning Abstract Because of new emission and on board diagnostics legislations, heavy truck manufacturers are facing new challenges when it comes to improving the en- gines and the control software. Accurate and real time executable engine models are essential in this work. One successful way of lowering the NOx emissions is to use Exhaust Gas Recirculation (EGR). The objective of this thesis is to create a mean value model for Scania’s next generation EGR system consisting of a poppet valve and a two stage cooler. -

Engine Cylinder Head Installation
Engine Cylinder Head Installation Important: Install the cylinder head without the camshafts. 1. Install the engine cylinder head to the engine block. 2. Install the AIR pump bolt and fir tree fastener from the back of the cylinder head. Refer to Service Bulletin 06-06-04-016A for further information. 3. Install new cylinder head bolts and tighten the bolts. Refer to Cylinder Head Replacement in SI. Camshaft Holding Tool Caution: The camshaft holding tools must be installed on the camshafts to prevent camshaft rotation. When performing service to the valve train and/or timing components, valve spring pressure can cause the camshafts to rotate unexpectedly and can cause personal injury. Important: Before installing the camshafts, refer to Camshafts Cleaning and Inspection in SI. 4. Install the camshafts with the flats up using the J 44221 - Camshaft Holding Tool. Refer to Camshaft Installation in SI. Notice: Tension must be always kept on the intake side of the timing chain to properly keep the engine in time. If the chain is loose the timing will be off, which may cause internal engine damage or set DTC P0017. Fastener Notice: Use the correct fastener in the correct location. Replacement fasteners must be the correct part number for that application. Fasteners requiring replacement or fasteners requiring the use of thread locking compound or sealant are identified in the service procedure. Do not use paints, lubricants, or corrosion inhibitors on fasteners or fastener joint surfaces unless specified. These coatings affect fastener torque and joint clamping force and may damage the fastener. Use the correct tightening sequence and specifications when installing fasteners in order to avoid damage to parts and systems. -

Enlarging Exhaust Ports
1.3mm/0.050in wide and a normal three angle valve seat is very suitable (45 degree seat/30 degree top cut/60 degree inner cut). The inner cut blends the 45 degree valve seat into the port throat and the top cut blends the 45 degree valve seat into the combustion chamber. The whole exhaust port passage- way must be enlarged throughout. The valve throat is ground or bored out to 34.5mm/1.358in and the original valve seat machined to suit the new valve size. The port outlet is taken out to the size of the exhaust manifold gasket aperture (oversize - lmm more height and width - exhaust manifold gaskets are available). The passage- way is ground out quite extensively, but note that while the floor of the port should be cleaned up it should not have any serious amount of material The areas of the combustion chamber to be reworked are shown here (see text for key). removed from it, especially where the The amount of material that is removed does vary depending on the proximity of the port runs into the valve throat area. gasket and bore wall. The sides of the exhaust ports and the to the full size of the standard gasket of gasket is used). This modification roof certainly have plenty of material using the gasket as a template. Over- gives a considerable increase in which can be removed and, once sized gaskets which allow an even exhaust port area because the stand- modified, bear little resemblance to the larger port exit cross-sectional area are ard 'as-cast' dimensions at this same originals. -

Analysis of Exhaust Manifold Using Computational Fluid Dynamics
cs: O ani pe ch n e A c Teja et al., Fluid Mech Open Acc 2016, 3:1 M c d e i s u s l F Fluid Mechanics: Open Access ISSN: 2476-2296 Research Article Open Access Analysis of Exhaust Manifold using Computational Fluid Dynamics Marupilla Akhil Teja*, Katari Ayyappa, Sunny Katam and Panga Anusha SIR C R Reddy College of Engineering, Andhra University, Vizag, India Abstract Overall engine performance of an engine can be obtained from the proper design of engine exhaust systems. With regard to stringent emission legislation in the automotive sector, there is a need design and develop suitable combustion chambers, inlet, and outlet manifold. Exhaust manifold is one of the important components which affect the engine performance. Flow through an exhaust manifold is time dependent with respect to crank angle position. In the present research work, numerical study on four-cylinder petrol engine with two exhaust manifold running at constant speed of 2800 rpm was studied. Flow through an exhaust manifold is dependent on the time since crank angle positions vary with respect to time. Unsteady state simulation can predict how an intake manifold work under real conditions. The boundary conditions are no longer constant but vary with time. The main objectives that to be studied in this work is: • To prepare the cad model in the CATIA software by using the actual parametric dimensions. • To prepare finite element model in the Computer aided analysis software by specifying the approximate element size for meshing. •To find and calculate the actual theoretical values for the input boundary conditions. -

Performer Rpm 330-403 Manifold Instructions
PERFORMER RPM 330-403 MANIFOLD CATALOG #7111 MODEL: Oldsmobile 330/350/403 c.i.d. V8 INSTRUCTIONS • PLEASE study these instructions, and the General Instructions, carefully before installing your new manifold. If you have any ques- tions or problems, do not hesitate to call our Technical Hotline at: 1-800-416-8628, 8am-12:30 and 1:30-5pm PST, weekdays. • EGR SYSTEM: This manifold will not accept stock EGR (exhaust gas recirculation) equipment. EGR systems are used on some 1972 and later model vehicles and only in some states. Check local laws for requirements. Not legal in California on pollution-con- trolled motor vehicles. • MANIFOLD: The Edelbrock Performer RPM 330-403 is a new generation manifold for 330, 350, and 403 c.i.d. small-block Oldsmobile engines. It may also be used on 1980-1/2—’85 307 c.i.d. Oldsmobile engines with 5A cylinder heads (casting #3317). Will not fit 1986 and newer 307 V8s with roller cams and swirl port heads. Port flange has extra material above the runner to allow for use with 455 heads. The Performer RPM 330-403 is a high-rise, two-plane design, engineered for a horsepower peak in the 6000- 6500 rpm range with a broader torque curve than single-plane manifolds in the lower rpm ranges. Recommended for high-perfor- mance street, strip and marine applications. The manifold accepts late model water neck, air conditioning, alternator and H.E.I. igni- tion systems. Use the recommended electric or manual choke carburetors only. NOTE: Carb mount pad is two inches taller than most stock manifolds, requiring hood clearance check. -

D8R 3406E and 3406C Engine Repair Options | Good Running Core 980H C15 Engine Level 1 Recondition
LONGER LIFE. ENGINE LOWER COST. D8R 3406E AND 3406C REBUILD OPTIONS BUTLERMACHINERY.COM/ENGINEREBUILD D8R 3406E AND 3406C D8R 3406E and 3406C Engine Repair Options | Good Running Core 980H C15 Engine Level 1 Recondition Repairs Level 1 Level 2 Level 3 Camshaft bearings X X X Coolant temperature regulator X X X Crankshaft thrust plates X X X Exhaust manifold studs/locknuts & exhaust sleeves X X X Gaskets & seals for components that are removed X X X Main bearings & rod bearings X X X Piston rings X X X PM service-oil, fuel and air filters X X X Turbocharger (mounting) studs/locknuts X X X Valve spring lock retainers, valve roto coils & exhaust valves X X X Recondition or replace engine oil pump X X X Replace engine breather X X Replace serpentine belt, coolant and fuel hoses integral to the engine X X Replace fuel injectors with Cat Reman X X Recondition or replace water pump X X Recondition or replace fuel transfer pump X X Recondition or replace turbo X X Dyno test engine X X Paint engine X X Sand engine block, polish crank, ceramic cylinder bores and water holes if needed X X Replace valve seats and valve guides X Integral engine harness X Engine related sensors, switches and fuel prime pump X Out-of-Frame Level 1 Replace engine oil cooler with reman X Out-of-Frame Level 2 Recondition or replace cylinder liner packs X Out-of-Frame Level 3 Hard parts found during disassembly and items noted under inspect/test that do not meet Cat reuse X guidelines, excludes major castings (engine block, crankshaft, front housing and rear housing) INCLUDES INSPECT/TEST PARTS/SERVICES PERFORMED • Camshaft • Liner protrusion & condition • Connecting rods • Piston spray jets Option Levels *Customer responsible for radiator testing and cleaning. -

Technology Overview
VQ35HR•VQ25HR Engine Technology Overview V6 GASOLINE ENGINE Advanced technology takes the next generation of Nissan’s world-renowned VQ engine to new pinnacles of high-rev performance and environmental friendliness. Nissan’s latest six-cylinder V-type Major technologies engine inherits the high-performance DNA that has made Nissan’s VQ Taking the award-winning VQ series another step series famous. Taking the acclaimed toward the ultimate powertrain, Nissan’s next- VQ engine’s “smooth transition” generation VQ35HR & VQ25HR are thoroughly concept to higher revolutions than reengineered to boost the rev limit and deliver greater ever, this VQ is a powerful and agile power, while achieving exceptional fuel economy and new powerplant for Nissan’s front- clean emissions. engine, rear-wheel-drive vehicles. Higher revolution limit By greatly reducing friction, Nissan engineers achieved a smooth transition to the high-rev limit, New VQ Engine which has been boosted to a 7,500rpm redline. Advantages Lengthened connecting rods Smooth transition up to high-rev redline Lengthening the connecting rods by 7.6mm reduces Lengthened connecting rods, addition of a ladder piston sideforce on the cylinder walls. This reduces frame and other improvements greatly reduce friction for smoother piston action to support high- friction. The result is effortless throttle response rev performance. all the way to the 7500-rpm redline. New ladder frame Top level power performance in class The lower cylinder block that supports the crankshaft Improved intake and exhaust systems, raised uses a ladder-frame structure for increased stiffness. combustion efficiency, and other enhancements This suppresses vibration to minimize friction at high achieve class-leading power. -

Exhaust Heat Risers Debunked – Myth and Fact
Exhaust Heat Risers – Fact and Fiction The Problem - Carburetor Icing Older automobiles and trucks had no heat risers. Their need was not even understood. Model A Fords never had them, nor did other automobiles of that era. As technical advancements took place and auto manufacturing proliferated, a problem developed. Engines would start and run fine for several minutes, but then would stall out briefly in chilly weather. Often the vehicle would drive for a mile or two, and then stall. This problem would typically occur once or twice, and then the engine would warm up enough that it ran fine. The problem only surfaced on chilly days when the temperature was between 32 and 40 degrees.. If the ambient temperature was higher or lower than these two points, the problem never materialized. It then became apparent that the issue was more noticeable on damp or rainy days, when humidity was high. The problem was exhibited most often on vehicles that were started up and driven just as soon as possible, with little or no warm-up time. In colder areas, many people learned to avoid the issue by simply letting the engine warm up for a few minutes before beginning to drive. The cold stalling issue never developed on stationary engines, tractors, larger trucks or construction equipment because typically these applications were given a few minutes of warm-up time. Also, industrial applications for many engines typically called for most of their use at fixed speeds. Parts books reveal that Dodge Pilothouse trucks up to and including one-ton size were equipped with heat riser valves in the forties and fifties. -
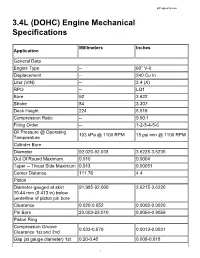
3.4L (DOHC) Engine Mechanical Specifications
60DegreeV6.com 3.4L (DOHC) Engine Mechanical Specifications Millimeters Inches Application General Data Engine Type -- 60° V-6 Displacement -- 240 Cu In Liter (VIN) -- 3.4 (X) RPO -- LQ1 Bore 92 3.622 Stroke 84 3.307 Deck Height 224 8.818 Compression Ratio -- 9.50:1 Firing Order -- 1-2-3-4-5-6 Oil Pressure @ Operating 103 kPa @ 1100 RPM 15 psi min @ 1100 RPM Temperature Cylinder Bore Diameter 92.020-92.038 3.6228-3.6235 Out Of Round Maximum 0.010 0.0004 Taper -- Thrust Side Maximum 0.013 0.00051 Center Distance 111.76 4.4 Piston Diameter-gauged at skirt 91.985-92.000 3.6215-3.6220 10.44 mm (0.413 in) below centerline of piston pin bore Clearance 0.020-0.052 0.0008-0.0020 Pin Bore 23.003-23.010 0.9056-0.9059 Piston Ring Compression Groove 0.033-0.079 0.0013-0.0031 Clearance 1st and 2nd Gap (at gauge diameter) 1st 0.20-0.45 0.008-0.018 1 60DegreeV6.com Gap (at gauge diameter) 2nd 0.56-0.81 0.022-0.032 Oil Groove Clearance 0.028-0.206 0.0011-0.0081 Gap (segment at gauge 0.25-0.76 0.0098-0.0299 diameter) Tension 1st 27.6 N 6.2 lbs Tension 2nd 19.8 N 4.5 lbs Tension Oil 31.2 N 7.0 lbs Piston Pin Diameter 22.9915-22.9964 0.9052-0.9054 Clearance 0.0066-0.0185 0.00026-0.00073 Fit In Rod 0.0165-0.0464 0.0006-0.0018 Crankshaft Main Journal Diameter-All 67.239-67.257 2.6472-2.6479 Taper-Maximum 0.005 0.0002 Out Of Round-Maximum 0.005 0.0002 Cylinder Block Main Bearing 72.155-72.168 2.8407-2.8412 Bore Diameter Crankshaft Main Bearing Inner 67.289-67.316 2.6492-2.6502 Diameter Main Bearing Clearance 0.019-0.064 0.0008-0.0025 Main Thrust Bearing Clearance -

DESIGN MODIFICATION and ANALYSIS of ENGINE EXHAUST MANIFOLD S.B.Borole1, Dr
International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395 -0056 Volume: 03 Issue: 09 | Sep-2016 www.irjet.net p-ISSN: 2395-0072 DESIGN MODIFICATION AND ANALYSIS OF ENGINE EXHAUST MANIFOLD S.B.Borole1, Dr. G.V.Shah2 [email protected] [email protected] Mechanical Engineering Department, P.V.P.I.T. Bavdhan, Pune University, Pune, Maharashtra, India ---------------------------------------------------------------------***--------------------------------------------------------------------- Abstract - This study focuses on the development of a thermal stresses while welding [4]. This stresses weakens reliable approach to predict failure of exhaust system fitting the materials, produces the defects, which can take shape of and on the removal of structural weaknesses through the small pieces of material, weld spatter, may loose and end up optimization of design. The task with this project was to find a destroying the catalytic converter [5]. Other defects can new solution concept for the connection of pipes into flanges in occur in the welding seam and they must be repaired manifolds. The concept that uses today for their manifolds is manually. However, the manifold should not be based on welding the pipes into place in the flange. The manufactured by casting, because the high temperatures in product development model that is used in this project is present combustion engines demand more expensive and written by Fredy Olsson. For this project have the parts high quality materials that causes problem when casting [7] “Principal construction” and” Primary construction” been [2]. The goal in the development of exhaust system fitting is used. to analyze several solutions weldless. The solutions that are The Objective is to present experimentation, modeling subject for further development are prepared during the and analysis of exhaust system fitting weldless by using FEA. -

Manifold Optimization of an Internal Combustion Engine by Using Thermal Analysis
IARJSET ISSN (Online) 2393-8021 ISSN (Print) 2394-1588 International Advanced Research Journal in Science, Engineering and Technology ISO 3297:2007 Certified Vol. 3, Issue 11, November 2016 Manifold Optimization of an Internal Combustion Engine by using Thermal Analysis V. Ashok Kumar1, M. Madhavi 2, A. Krishna3 Associate Professor, Mechanical Engineering, Mother Theressa College of Engg & Tech, Peddapalli, Telangana1 M.Tech, Student, Mechanical Engineering, Mother Theressa College of Engg & Tech, Peddapalli, Telangana2 Assistant Professor, Mechanical Engineering, Mother Theressa College of Engg & Tech, Peddapalli, Telangana3 Abstract: In this thesis, an exhaust manifold modelled by PRO-E design software. The thesis will focus on CFD and thermal analysis with different loads (2, 6,12,14,16 and 18 kg). Thermal analysis done for the exhaust manifold by cast iron, stainless steel, silicon nitride& zinc oxide. In this thesis the CFD analysis to determine the heat transfer rate, mass flow rate, pressure drop and thermal analysis to determine the temperature distribution, heat flux with different materials. 3D modeled in parametric software Pro-Engineer and analysis done in ANSYS. Keywords: Exhaust Manifold, IC Engine, CFD Modeling for Exhaust Manifold. I. INTRODUCTION In automotive engineering, an exhaust manifold collects This is often used on performance production cars and the exhaust gases from multiple cylinders into one pipe. track-only racers. Exhaust wrap is wrapped completely The word manifold comes from the Old English word around the manifold. Although this is cheap and fairly manifold (from the Anglo-Saxon mani [many] and fold simple, it can lead to premature degradation of the [fold]) and refers to the folding together of multiple inputs manifold. -

A Design Strategy for Volumetric Efficiency Improvement in a Multi-Cylinder Stationary Diesel Engine and Its Validity Under Transient Engine Operation
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Directory of Open Access Journals SCI-PUBLICATIONS American Journal of Applied Sciences 5 (3): 189-196, 2008 ISSN 1546-9239 © 2008 Science Publications A Design Strategy for Volumetric Efficiency Improvement in a Multi-cylinder Stationary Diesel Engine and its Validity under Transient Engine Operation 1P. Seenikannan, 2V.M.Periasamy and 3P.Nagaraj 1 Author Manuscrip Deptartment of Mech., Sethu Institute of Tech., Kariapatti, T.N, India, 626106 2 Crescent Engineering College, Chennai, T.N, India 3Deptartmentof Mech, Mepco Schlenk Engg College, T.N., India Abstract: This paper proposes an approach to improve engine performance of volumetric efficiency of a multi cylinder diesel engine. A computer simulation model is used to compare volumetric efficiency with instantaneous values. A baseline engine model is first correlated with measured volumetric efficiency data to establish confidence in the engine model’s predictions. A derivative of the baseline model with exhaust manifold, is then subjected to a transient expedition simulating typical, in-service, t maximum rates of engine speed change. Instantaneous volumetric efficiency, calculated over discrete engine cycles forming the sequence, is then compared with its steady speed equivalent at the corresponding speed. It is shown that the engine volumetric efficiency responds almost quasi-steadily under transient operation thus justifying the assumption of correlation between steady speed and transient data. The computer model is used to demonstrate the basic gas dynamic phenomena graphically. The paper provides a good example of the application of computer simulation techniques in providing answers to real engineering questions.