Belt and Chain Drives (Flexible Drive Elements)
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Engine Components and Filters: Damage Profiles, Probable Causes and Prevention
ENGINE COMPONENTS AND FILTERS: DAMAGE PROFILES, PROBABLE CAUSES AND PREVENTION Technical Information AFTERMARKET Contents 1 Introduction 5 2 General topics 6 2.1 Engine wear caused by contamination 6 2.2 Fuel flooding 8 2.3 Hydraulic lock 10 2.4 Increased oil consumption 12 3 Top of the piston and piston ring belt 14 3.1 Hole burned through the top of the piston in gasoline and diesel engines 14 3.2 Melting at the top of the piston and the top land of a gasoline engine 16 3.3 Melting at the top of the piston and the top land of a diesel engine 18 3.4 Broken piston ring lands 20 3.5 Valve impacts at the top of the piston and piston hammering at the cylinder head 22 3.6 Cracks in the top of the piston 24 4 Piston skirt 26 4.1 Piston seizure on the thrust and opposite side (piston skirt area only) 26 4.2 Piston seizure on one side of the piston skirt 27 4.3 Diagonal piston seizure next to the pin bore 28 4.4 Asymmetrical wear pattern on the piston skirt 30 4.5 Piston seizure in the lower piston skirt area only 31 4.6 Heavy wear at the piston skirt with a rough, matte surface 32 4.7 Wear marks on one side of the piston skirt 33 5 Support – piston pin bushing 34 5.1 Seizure in the pin bore 34 5.2 Cratered piston wall in the pin boss area 35 6 Piston rings 36 6.1 Piston rings with burn marks and seizure marks on the 36 piston skirt 6.2 Damage to the ring belt due to fractured piston rings 37 6.3 Heavy wear of the piston ring grooves and piston rings 38 6.4 Heavy radial wear of the piston rings 39 7 Cylinder liners 40 7.1 Pitting on the outer -

Timing Belt Interference Caution Note: Camshaft
Carmax 6067 170 Turnpike Rd Westborough, MA 01581 YMMS: 1991 Chevrolet Lumina Z34 Sep 3, 2020 Engine: 3.4L Eng License: VIN: Odometer: TIMING BELT INTERFERENCE CAUTION NOTE: CAMSHAFT DRIVE BELTS OR TIMING BELTS - The condition of camshaft drive belts should always be checked on vehicles which have more than 50,000 miles. Although some manufacturers do not recommend replacement at a specified mileage, others require it at 60,000-100,000 miles. A camshaft drive belt failure may cause extensive damage to internal engine components on most engines, although some designs do not allow piston-to-valve contact. These designs are often called "Free Wheeling". Many manufacturers changed their maintenance and warranty schedules in the mid-1980's to reflect timing belt inspection and/or replacement at 50,000- 60,000 miles. Most service interval schedules shown in this section reflect these changes. Belts or components should be inspected and replaced if any of the following conditions exist: Crack Or Tears In Belt Surface Missing, Damaged, Cracked Or Rounded Teeth Oil Contamination Damaged Or Faulty Tensioners Incorrect Tension Adjustment REMOVAL & INSTALLATION Tip: Timing belt CAUTION: For 1996-97 models, this application is an interference engine. Do not rotate camshaft or crankshaft when timing belt is removed, or engine damage may occur. NOTE: The camshaft timing procedure has been updated by TSB bulletin No. 47-61-34, dated December, 1994. REMOVAL Tip: timing 3.4 x motor 1. Disconnect negative battery cable. Remove air cleaner and duct assembly. Drain engine coolant. 2. Remove accelerator and cruise control cables from throttle body. -

Belt Drive Systems: Potential for CO2 Reductions and How to Achieve Them
19 Belt drive 19 Belt drive Belt drive 19 Belt drive systems Potenti al for CO2 reducti ons and how to achieve them Hermann Sti ef Rainer Pfl ug Timo Schmidt Christi an Fechler 19 264 Schaeffl er SYMPOSIUM 2010 Schaeffl er SYMPOSIUM 2010 265 19 Belt drive Belt drive 19 If required, double-row Introducti on Tension pulleys and angular contact ball Single and double eccentric tensioners bearings (Figure 3) are Schaeffl er has volume produced components for idler pulleys used that also have an belt drive systems since 1977. For the past 15 years, opti mized grease sup- Schaeffl er has worked on the development of com- One use of INA idler pulleys is to reduce noise in ply volume. These plete belt drive systems in ti ming drives (Figure 1) criti cal belt spans, to prevent collision problems bearings are equipped as well as in accessory drives (Figure 2). with the surrounding structure, to guide the belt with high-temperature or to increase the angle of belt wrap on neighbor- rolling bearing greases ing pulleys. These pulleys have the same rati ng and appropriate seals. life and noise development requirements as belt Standard catalog bear- tensioning systems. For this applicati on, high-pre- ings are not as suitable Pulleys Variable camsha ming cision single-row ball bearings with an enlarged for this applicati on. grease supply volume have proven suffi cient. The tension pulleys in- stalled consist of single or double-row ball bearings specially de- veloped, opti mized and manufactured by INA for use in belt drive ap- Idler pulleys plicati ons. -
Decoupled Pulley Fax +49 6201 25964-11 Fax +39 0121 369299
The typical crankshaft vibrations are compensated by employing high quality decoupled belt pulleys. This minimizes the transmission of vibrations to other vehicle components and the associated effects on the entire vehicle. So you can enjoy undisturbed ride comfort. CORTECO GmbH CORTECO S.r.l.u. SEALING VIBRATION CONTROL CABIN AIR FILTER Badener Straße 4 Corso Torino 420/D 69493 Hirschberg 10064 Pinerolo (TO) Germanny Italy Corteco original quality Tel. +49 6201 25964-0 Tel. +39 0121 369269 Decoupled PULLEY Fax +49 6201 25964-11 Fax +39 0121 369299 CORTECO S.A.S. CORTECO Ltd. Z.A. La Couture Unit 6, Wycliffe Industrial 87140 Nantiat Park Complex inner workings: France Lutterworth The decoupled belt pulley Tel. +33 5 55536800 Leicestershire is joined to the torsional Fax +33 5 55536888 LE17 4HG vibration damper by a United Kingdom highly elastic elastomer Tel. +44 1455 550000 part, thereby offering opti- www.corteco.com Fax +44 1455 550066 mum damping properties. 19036674 SIG-08/2012 THE belt DRIVE MOVES A EXPENSIVE economic Satisfied customers NUMBER OF THINGS MEASURES ARE GOOD customers No matter whether a drive belt is too loud or ancillary units are damaged by vibration – belt drive decoupling deficiencies are always associated with dissatisfaction. Anyone not using original parts for a decoupled belt pul- ley is making a false saving. Cheap counterfeit products generally lead to complaints after a short running time and loss of customer confidence. On the other hand, ori- ginal parts from CORTECO still work reliably, often after 100,000 kilometers. Transmission of crankshaft vibrations to ancillary units can produce an increased noise level, severe wear of adjoi- Original: after 100,000 km in the vehicle The decoupled belt pulley should be checked after about ning components and undesirable vehicle vibration. -

C6 Corvette Supercharger Kit Instructions ECS SC 600 Instructions (C6)
C6 Corvette Supercharger Kit Instructions ECS SC 600 Instructions (C6) These instructions are meant to serve as a guide to the installation of the ECS SC600 Supercharging kit. Please be sure to use all safety equipment including gloves, and eye protection. Please use proper techniques to capture and dispose of, or reuse factory fluids. Utilization of the proper tools will make the install smoother and faster. If you are having ECS provide you with a start up tune, your first step should be to remove your PCM, and ship immediately so that you can have it back ready for start up. Our shipping address is 562 Rt. 539, Cream Ridge, NJ, 08514. Installation should take between 1012 andto 15 20 hours hours for a qualified mechanic. Do not rush the install. If need technical support please call the shop at 609-752-0321. ECS SC600 Kit Installation: • Remove fuel Rail covers, and disconnect battery terminals with 10 MM wrench. • Remove cap from coolant reservoir and proceed to drain coolant by turning radiator drain cock one ¼ turn to the left. • Remove stock serpentine beltbet by placing 15mm wrench on tensioner bolt and press towards intake and pulling bet forward off tensioner • Remove stock tensioner by removing the 2 15mm bolts with socket. Save bolts for later use. • Remove hard plastic vacuum line from passenger side valve cover (Fig.1) 1 • Remove 15 mm bolt and bracket holding Evap solenoid to passenger side head and discard. Evap solenoid stays in place. (Fig.2) • DisconnectOn the drivers MAF side and of thenthe car, remove remove stock alternator air bridge wiring and filterharness assembly from top from of alternator car by loosening and positive clamps alternator and pulling wire forwardby removing and up 13mm off throttle retaining body. -

ASME/ANSI RS Roller Chain Technical Information
U.S. TSUBAKI RS ROLLER CHAIN U.S. TSUBAKI ROLLER CHAIN — A SOLID DIFFERENCE ASME/ANSI RS Roller Chain A - DRIVE CHAINS RS ROLLER CHAIN RS11 ˜ RS240 Longer Wear Life Higher Horsepower Ratings Greater Fatigue Strength U.S. Tsubaki Roller Chain lasts up to U.S. Tsubaki ASME/ANSI Chains handle U.S. Tsubaki ASME/ANSI Chains are twice as long as our previous chain in up to 33 percent more horsepower so you designed to have higher fatigue strength. many applications. Advanced technology can increase drive performance without The wider waist of the link plates puts allows us to combine the strength, increasing chain size. In fact, depending more metal where you need it — running durability, and reliability of a solid bushing on your application, you may be able to your application. There is less downtime with our patented lube groove on the transmit the same horsepower with a because chains operate longer. Operating inner surface of sizes RS80 through smaller, less costly chain. The costs are reduced because chains RS140. The solid bushings are precise improvement comes from a U.S. Tsubaki perform more efficiently. These benefits round cylinders, which means better exclusive ring coining process for the slip go right to your bottom line. contact between the pin and bushing. The fit connecting link and special processing lube grooves hold oil where chain needs on the two-pitch offset link. S-N Curve it most. The result is longer lasting chain. Horsepower Ratings Wear Elongation Curve A & a: Fatigue strength B & b: Tensile strength Improved Tsubaki B Chain b Competitor A Competitor B Previous Improved Previous Tsubaki Tsubaki Tsubaki Improved Tsubaki Chain Chain Chain Chain 1.5 33% Increase in Horespower Rating 1.0 RS80-RS140 Other roller chain A .05 "S" Chain load a HP HP 2 3 4 5 6 7 Elongation (%) * Ratings are for RS80-RS240 Roller Chains 1 10 10 0 50 100 150 200 Revs Per Minute (RPM) 10 10 10 10 10 Time (Hours) "N" Number of times load is applied Save Time & Money Wear in the pin-bushing joint can lead to elongation and replacement. -

Chapter 1 Introduction
國立交通大學 機械工程研究所 碩士論文 變速自行車鏈條設計 Design of Chains on Multi-speed Bicycles 研究生:張崇銘 指導教授:曾錦煥 教授 中華民國九十三年六月 變速自行車鏈條設計 Design of Chains on Multi-speed Bicycles 研究生:張崇銘 Student: Chung-Ming Chang 指導教授:曾錦煥 Advisor: Ching-Huan Tseng 國立交通大學 機械工程研究所 碩士論文 A Thesis Submitted to Institute of Mechanical Engineering College of Engineering National Chiao Tung University in Partial Fulfillment of the Requirements for the Degree of Master of Science in Mechanical Engineering June 2004 Hsinchu, Taiwan, Republic of china 中華民國九十三年六月 變速自行車鏈條設計 研究生:張崇銘 指導教授:曾錦煥 國立交通大學機械工程研究所 摘要 本論文主要研究對象為自行車上傳動系統中的鏈條元件,由於自行車飛 輪受到車架、騎乘姿勢所形成的空間限制,必須在有限空間內增加飛輪片 數增加齒數比,達到變速換檔的舒適性。因此,為了配合這樣緊密的飛輪, 鏈條寬度的縮減是必須的。經過專利的整理後,確定空間尺寸和強度為初 步設計的主要需求;提出不同的概念設計,並利用新的鏈條連結機構來達 到鏈條寬度的縮減。 本文提出概念設計較目前市面上自行車最窄的鏈條寬度更窄,強度部份 利用有限元素分析法做定性分析,比較各個設計的相對強度;此外也經由 原型的製作,檢視其機構的問題。 i Design of Chain on Multi-speed Bicycle Student: Chung-Ming Chang Advisor: Ching-Huan Tseng Institute of Mechanical Engineering National Chiao Tung University ABSTRACT This study focuses on the chain for the multi-speed bicycle. Design space for the freewheel on bicycle is limited by frame, riding posture, etc. However, the number of gear ratios in this design space increased with added more sprockets are the trend on the bicycles. Therefore, reduction of chain width is necessary for working with this compact freewheel. Space and strength are main requirements in the beginning of design according to literatures and patents review. Several new concepts are proposed, and these concepts use the linkage mechanism to achieve the reduction of chain width. Chain width of these concepts proposed in this study can be reduced under the assumption for fixed design space and thickness of sprockets. The finite element method is used to compare the trend of strength among these concepts. -

Diesel Engine Starting Systems Are As Follows: a Diesel Engine Needs to Rotate Between 150 and 250 Rpm
chapter 7 DIESEL ENGINE STARTING SYSTEMS LEARNING OBJECTIVES KEY TERMS After reading this chapter, the student should Armature 220 Hold in 240 be able to: Field coil 220 Starter interlock 234 1. Identify all main components of a diesel engine Brushes 220 Starter relay 225 starting system Commutator 223 Disconnect switch 237 2. Describe the similarities and differences Pull in 240 between air, hydraulic, and electric starting systems 3. Identify all main components of an electric starter motor assembly 4. Describe how electrical current flows through an electric starter motor 5. Explain the purpose of starting systems interlocks 6. Identify the main components of a pneumatic starting system 7. Identify the main components of a hydraulic starting system 8. Describe a step-by-step diagnostic procedure for a slow cranking problem 9. Describe a step-by-step diagnostic procedure for a no crank problem 10. Explain how to test for excessive voltage drop in a starter circuit 216 M07_HEAR3623_01_SE_C07.indd 216 07/01/15 8:26 PM INTRODUCTION able to get the job done. Many large diesel engines will use a 24V starting system for even greater cranking power. ● SEE FIGURE 7–2 for a typical arrangement of a heavy-duty electric SAFETY FIRST Some specific safety concerns related to starter on a diesel engine. diesel engine starting systems are as follows: A diesel engine needs to rotate between 150 and 250 rpm ■ Battery explosion risk to start. The purpose of the starting system is to provide the torque needed to achieve the necessary minimum cranking ■ Burns from high current flow through battery cables speed. -

Technical Engineering Guide
TTEECHCHNINICALCAL EN ENGGINEEINEERRININGG 89 www.diamondchain.com TECHNICAL ENGINEERING General Drive Considerations One of the main advantages of the roller chain drive is its ability to perform well under widely varying conditions. Despite this ability, there are a number of rules of good design practice which, if considered early in the design pro- cess, will enable the user to obtain desirable results. Basic dimensions and minimum ultimate tensile requirements for single-pitch, double-pitch and attachment roller chains are specified by various standards organizations worldwide. ASME/ANSI, The American Society of Mechanical Engineers and The American National Standards Institute, defines dimensions such as: pitch, roller width, roller diameter, link plate height, link plate thickness and pin diameter. The primary purpose of the standard is to ensure that manufacturers will produce chains and sub-assemblies that are similar dimensionally and therefore interchangeable. In addition, the standard does offer the user some assurance of quality by defining a minimum ultimate tensile strength for each model of chain. However, tensile strength is not always a valid method to differentiate one manufacturer’s product from another. It is very important to remember that dimensional standardization does not define quality or performance characteristics. Minimum Ultimate Tensile Strength: Minimum Ultimate Tensile Strength, MUTS, is the static load required to break the chain. Tensile strength values shown in this catalog are not allowable working loads. Load or tension applied 1 to the chain in service should never exceed ⁄6 th of the UTS. If exceeding this value is necessary for a specific applica- tion, contact Diamond Chain. -

WT Series Actuator Operations Manual WATCH TECHNOLOGIES W T S E R I E S Actuator Operations Manual
Water Control Devices WT Series Actuator Operations Manual WATCH TECHNOLOGIES W T S E R I E S Actuator Operations Manual Watch Technologies 2185 NE Spalding Ave, #10 Grants Pass, OR 97526 Phone 541.472.8095 06/2016 Contents Introduction ………………………………………………............ 1 Theory of Operation ………………………………………. 1 Installation and Start-up ………………………………………… 3 Safety Information ………………………………………… 3 Installation – Rising Stem ………………………………… 4 Installation – Horizontal Gearlift …………………………. 12 Seasonal Start-Up ………………………………………………. 16 Operation ………………………………………………………… 18 Manual Operation ………………………………………… 19 Automated Operation Using Internal RTU ……………… 20 Handwheel Operation …………………………………….. 20 Maintenance and Troubleshooting ……………………………. 21 Troubleshooting Guide …………………………………… 22 Shut-Down and Storage ………………………………………... 23 System Integration and Options ………………………………. 24 Electrical System …………………………………………. 24 Gate Blade Position Sensor ………………………………25 Solar Panel and Charge Controller ……………………... 27 RUG3 Remote Terminal Unit ……………………………. 28 WT Actuator and Gearmotor Specifications ……………29 – 39 Warranty Information …………………………………………… 41 WATER CONTROL DEVICE S Introduction The WT Series of gate control actuators from Watch Technologies have been developed for the ultimate control of a wide variety of applications. he WT Series consists of five distinct models to address the needs of both vertical rising stem gate users as well as systems utilizing T horizontal shaft gear lifts. A wide variety of drive motors enable the WT Series to align with specific torque requirements. The WT Series can also be configured with an embedded Remote Terminal Unit (RTU) which enables the actuator to function as a stand-alone, smart device that can remotely control gates based upon user-defined control points and water status parameters (flow, level). Theory of Operation The philosophy behind each Watch Technologies product is providing long- lived, reliable devices that can be easily installed, maintained, adjusted and upgraded by our customers using simple tools and basic skills. -

Roller Drive Chain Selection and Engineering Information
sec_29.3_29.4_TI 11/19/08 12:45 PM Page 231 Roller Drive Chain Selection 29 Roller Drive Chain Selection and Engineering Information Required information for drive selection: Table 1: Service Factors 1. Type of input power (electric motor, internal combustion Type of Input Power engine, etc.). Internal Internal 2. Type of equipment to be driven. Class of Driven Combustion Combustion Electric Motor 3. Horsepower (HP) to be transmitted. Load Engine with Engine with or Turbine Information Technical Mechanical 4. Full load speed of the fastest running shaft (RPM). Hydraulic Drive Drive 5. Desired speed of the slow-running shaft. NOTE: If the speeds are variable, determine the horsepower to be Uniform 1 1 1.2 transmitted at each speed. Moderate 1.2 1.3 1.4 6. Diameters of the driver and driven shafts. Heavy 1.4 1.5 1.7 7. Center distance of the shafts. NOTE: If this distance is adjustable, determine the Step 3: Calculate the Design Horsepower. amount of adjustment. Design Horsepower = HP x Service Factor 8. Position of drive and space limitations (if any). 9. Conditions of the drive. Drives with more than two The design horsepower equals the horsepower to be sprockets, idlers, or unusual conditions such as severely transmitted times the service factor found in Table 1. abrasive or corrosive environments, severely high or low temperatures, widely fluctuating loads, frequent starts Step 4: Select the Chain Pitch. and stops, etc., require special attention. It is advisable From the Quick Selector Chart on page 234, make a to consult with Renold Jeffrey engineering personnel in tentative chain selection as follows: these situations. -
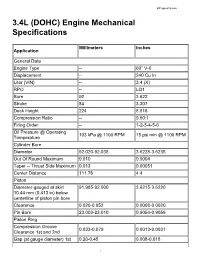
3.4L (DOHC) Engine Mechanical Specifications
60DegreeV6.com 3.4L (DOHC) Engine Mechanical Specifications Millimeters Inches Application General Data Engine Type -- 60° V-6 Displacement -- 240 Cu In Liter (VIN) -- 3.4 (X) RPO -- LQ1 Bore 92 3.622 Stroke 84 3.307 Deck Height 224 8.818 Compression Ratio -- 9.50:1 Firing Order -- 1-2-3-4-5-6 Oil Pressure @ Operating 103 kPa @ 1100 RPM 15 psi min @ 1100 RPM Temperature Cylinder Bore Diameter 92.020-92.038 3.6228-3.6235 Out Of Round Maximum 0.010 0.0004 Taper -- Thrust Side Maximum 0.013 0.00051 Center Distance 111.76 4.4 Piston Diameter-gauged at skirt 91.985-92.000 3.6215-3.6220 10.44 mm (0.413 in) below centerline of piston pin bore Clearance 0.020-0.052 0.0008-0.0020 Pin Bore 23.003-23.010 0.9056-0.9059 Piston Ring Compression Groove 0.033-0.079 0.0013-0.0031 Clearance 1st and 2nd Gap (at gauge diameter) 1st 0.20-0.45 0.008-0.018 1 60DegreeV6.com Gap (at gauge diameter) 2nd 0.56-0.81 0.022-0.032 Oil Groove Clearance 0.028-0.206 0.0011-0.0081 Gap (segment at gauge 0.25-0.76 0.0098-0.0299 diameter) Tension 1st 27.6 N 6.2 lbs Tension 2nd 19.8 N 4.5 lbs Tension Oil 31.2 N 7.0 lbs Piston Pin Diameter 22.9915-22.9964 0.9052-0.9054 Clearance 0.0066-0.0185 0.00026-0.00073 Fit In Rod 0.0165-0.0464 0.0006-0.0018 Crankshaft Main Journal Diameter-All 67.239-67.257 2.6472-2.6479 Taper-Maximum 0.005 0.0002 Out Of Round-Maximum 0.005 0.0002 Cylinder Block Main Bearing 72.155-72.168 2.8407-2.8412 Bore Diameter Crankshaft Main Bearing Inner 67.289-67.316 2.6492-2.6502 Diameter Main Bearing Clearance 0.019-0.064 0.0008-0.0025 Main Thrust Bearing Clearance