Metabolic Factors Limiting Performance in Marathon Runners
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Nutrition in Action
Nutrition For Sports Performance How to fuel your body for sports and health • Many active people faithfully train to improve their performance but they fail to get the most out of their workouts. Nutrition is their missing link. What is Sports Nutrition? • The practical science of – hydrating and fueling – before, during, and after exercise. • Executed properly, sports nutrition can help promote optimal training and performance. • Done incorrectly or ignored, it can derail training and hamper performance. THE 3 PRINCIPLES OF SPORTS NUTRITION - Provide fuel for your 1. Provide fuel for your muscles – muscles. - Stay hydrated. 2. Stay hydrated – - Promote optimal 3. Promote optimal recovery after – recovery after exercise.exercise What are the best energy foods? • . Carbohydrates! Without question, because carbohydrates (as compared to protein and fat) best fuel your muscles with the energy you need to exercise. Fueling Your Body .Carbohydrates are the primary fuel for most types of exercise. .60–90 minutes of endurance training or a few hours in the weight room can seriously deplete carbohydrate muscle fuel stores. .If your diet is too low in carbs, your workouts and performance will suffer. .Starting exercise with full carbohydrate stores can delay the onset of fatigue and help you train and compete more effectively. .The more intense your training or competition, the higher your daily carbohydrate intake should be in the suggested range of 2.3–4.5 grams of carbs per lb body weight daily. (That’s 345-675g/day for 150 lb athlete) Fueling There are two forms of • When you’re fully loaded carbohydrate in your body: with carbs, you have: . -

Occasional Article
J Clin Pathol: first published as 10.1136/jcp.42.11.1121 on 1 November 1989. Downloaded from J Clin Pathol 1989;42:1121-1 125 Occasional article Chemistry of marathon running A C AMES From the Department ofChemical Pathology, Neath General Hospital, Neath, West Glamorgan Introduction performance to be reached. Intensive training increases the maximal cardiac output and blood The upsurge of interest in the beneficial effects of volume of skeletal muscles, and by conditioning, exercise and participation in endurance events like increases the mitochondrial density, oxidative marathon running, which started in the early 1980's, enzymes, and myoglobin in muscle cells. These adap- has been maintained, and the 22000 competitors who tations combine to raise the maximal total body completed the 1989 London Marathon bear witness to oxygen consumption (V02 max), thus enabling greater the continuing involvement of a mass ofordinary men workloads to be tolerated with a consequent and women. Most who train and compete regularly improvement in endurance.2 undergo adaptive physiological changes, with During aerobic metabolism, intracellular muscle improved physical fitness and benefits to long term glycogen and triglyceride with extracellular glucose health. For a few, rigorous exercise is not without its and free fatty acids (FFA) are oxidised to provide copyright. hazards to health. energy. As glycogen stores become depleted during This review briefly and selectively outlines the prolonged exercise the relative contribution from FFA normal physiological responses, together with adverse increases, and this ability to oxidise FFA at any pathological effects and their clinical consequences intensity of exercise is an important adaptation of where appropriate. -

Marathon Freak Out
SURVIVING THE MARATHON FREAK OUT A Guide to Running Your Best Marathon GREG McMILLAN, M.S. Surviving the Marathon Freak Out Get the Latest and Greatest! With the purchase of this book, you now have another person (me) on your support team as you head into your marathon. I’m very much looking forward to working with you for the best marathon of your life. In order to help you get the most out of this Guide, step one is to “register” your book, which sounds more glamorous than it is. Just send an email to [email protected] to let me know you have the book. I can then keep you updated as I add to the book and have more tips and advice to share. Simple as that. © Greg McMillan, McMillan Running LLC | www.McMillanRunning.com 1 Surviving the Marathon Freak Out My Promise Don’t worry. It’s going to be okay. I promise. I know you’ve been training for the big day (a.k.a. marathon day) for a while now so it’s normal to get anxious as the day approaches. I’ve been there too. As a runner, I’ve dealt with the rigors of marathon training and the nervousness as the race nears, none more so than before my first marathon, the New York City Marathon or before I won the National Masters Trail Marathon Championships a few years ago. As a coach, I’ve trained thousands of runners just like you for marathons around the globe, in every weather condition and over all types of crazy terrain. -

Metabolic Factors Limiting Performance in Marathon Runners
Metabolic Factors Limiting Performance in Marathon Runners The MIT Faculty has made this article openly available. Please share how this access benefits you. Your story matters. Citation Rapoport BI (2010) Metabolic Factors Limiting Performance in Marathon Runners. PLoS Comput Biol 6(10): e1000960. doi:10.1371/ journal.pcbi.1000960 As Published http://dx.doi.org/10.1371/journal.pcbi.1000960 Publisher Public Library of Science Version Final published version Citable link http://hdl.handle.net/1721.1/64437 Terms of Use Creative Commons Attribution Detailed Terms http://creativecommons.org/licenses/by/2.5/ Metabolic Factors Limiting Performance in Marathon Runners Benjamin I. Rapoport1,2* 1 M.D.– Ph.D. Program, Harvard Medical School, Boston, Massachusetts, United States of America, 2 Department of Electrical Engineering and Computer Science and Division of Health Sciences and Technology, Massachusetts Institute of Technology, Cambridge, Massachusetts, United States of America Abstract Each year in the past three decades has seen hundreds of thousands of runners register to run a major marathon. Of those who attempt to race over the marathon distance of 26 miles and 385 yards (42.195 kilometers), more than two-fifths experience severe and performance-limiting depletion of physiologic carbohydrate reserves (a phenomenon known as ‘hitting the wall’), and thousands drop out before reaching the finish lines (approximately 1–2% of those who start). Analyses of endurance physiology have often either used coarse approximations to suggest that human -

“Bonk”? Mark Schecker, M.D
What’s up with the “Bonk”? Mark Schecker, M.D. Co-Founder, Vice President and Medical Director, Myrtle Beach Marathon There seems to be a lot of fuss these days about “bonking”. Without even knowing what it means the word just gives off a negative vibe. As a fuddy-duddy old dad who’d never heard the term before and didn’t know any better; had I overheard my daughters talking about bonking, I’d probably have run to get the nearest shotgun to track down the idiots they were planning to do it with. It doesn’t seem that long ago that runners, and in particular marathon runners, who ran into trouble during their event would “hit the wall” usually somewhere around the 18-20 mile mark. I’m all too familiar with the concept myself having met this unfortunate fate in both my marathon journeys. I swear that my nose is still at least a ½ inch flatter now, although those who know me might beg to differ. So as a marathon Medical Director I recently thought it incumbent upon me to familiarize myself with the nuances of “the bonk”; an obviously more hipper and fashionable version of the dreaded sequence of events behind all the fuss. For the better part of 60 years or so, since the early part of the last century, the cause of bonking (I.e., “hitting the wall”) was accepted as simply due to the body running out of fuel, particularly carbohydrates and more specifically glycogen. For those unfamiliar with either term and fortunate enough not to have had the experience, hitting the wall or bonking is a systemic collapse of multiple bodily functions during endurance events. -

Exercise Induced Collapse: "Hitting the Wall"
Exercise Induced Collapse: "Hitting the Wall" Background 1. "Hitting the Wall" / "Bonking" o Severe energy loss during prolonged exercise o Runners collapse around 20 mile point in marathon o Possibly due to depletion of muscle glycogen . Fat stores (even in leanest runners) are inexhaustible . Unable to utilize fat without carbohydrate as primer for metabolism Pathophysiology 1. Old theory: exhaustion of carbohydrate fuel o Muscle glycogen or blood glucose falls to critically low level o Glycogen depletion contributes to muscle fatigue . At 80 % maximum capacity o Glycogen content of muscles dropped near zero in 90 min . Marathon at normal pace o Fuel consumption ratio: . 75 % carbohydrates . 25% fatty acids o Carbohydrate supplies fall . Body relies on fatty acids o Body stores 2,000 calories of glycogen in muscles and liver . Enough for about 20 miles 2. New theory: CNS fatigue o Muscle damage may cause "hitting the wall" o Protective mechanism . Mediated by interleukin-6 Brain decreases muscle stimulation Discomfort/exhaustion when muscle damage approaches dangerous levels during prolonged exercise . Mediated by serotonin Prolonged exercise increases serotonin production Tryptophan-amino acid o Precursor to serotonin o Increase levels with muscle damage o Increased tryptophan . Leads to increased serotonin Increased serotonin causes brain to stimulate release of serum fatty acid Increased serum fatty acid causes increased CNS fatigue . Mediated by insulin Protein stimulates insulin release Insulin speeds muscle cells' absorption of blood glucose by 50% Transports amino acids into muscle Decreased release of stress hormone cortisol Stimulates blood flow to muscle Hitting the Wall Page 1 of 4 1.29.09 Diagnostics 1. -

NORTHERN ILLINOIS UNIVERSITY an Analysis of My Experience Training for and Running a Marathon a Thesis Submitted to the Universi
NORTHERN ILLINOIS UNIVERSITY An Analysis of My Experience Training for and Running a Marathon A Thesis Submitted to the University Honors Program In Partial Fulfillment of the Requirements of the Baccalaureate Degree With University Honors School of Allied Health Professions by Bridget Arne DeKalb, TIlinois Graduation Date: May 1999 Student name: 1'JurkR1u ~~~=-------------------- Approved by ~/kdI!dJUt Department of: ~W Utu:a.1tir2 Date: .h.rM. JiLl /CJq 7 HONORS THESIS ABSTRACT THESIS SUBMISSION FORM AUTHOR: Bridget Arne THESIS TITLE: An Analysis of My Experience Training for and Running a Marathon ADVISOR: Gail Guttenberg ADVISOR'S DEPT: Physical Education DISCIPLINE: Exercise Physiology YEAR: 1997 PAGE LENGTH: 18 BIBLIOGRAPHY: Yes ILLUSTRATED: No PUBLISHED (YES OR NO): No LIST PUBLICATION: N/A COPIES AVAILABLE (HARD COPY, MICROFILM, DISKETTE): Hard copy ABSTRACT (100-200 WORDS): This thesis is designed as a guide to runners wishing to run a marathon. Topics discussed in general are training techniques, the physiology of running, nutrition for runners, stress as it is related to running, and one's personality and running. The purpose of this thesis was for the author to learn about the general topics previously mentioned and by doing so learn about herself Also the experience of running a marathon was both a mental and physical challenge. The thesis is based on suggestions from other sources and from this author's one-time experience of training for and running a marathon. The author concluded that by running a marathon, one learns much about oneself, and she also concludes that if the experience was ever repeated, some modifications would be acted upon. -

Can Endurance Exercise Save the Western World?
antioxidants Review Re-Evaluating the Oxidative Phenotype: Can Endurance Exercise Save the Western World? Filip Kolodziej * and Ken D. O’Halloran Department of Physiology, School of Medicine, College of Medicine & Health, University College Cork, T12 XF62 Cork, Ireland; [email protected] * Correspondence: [email protected] Abstract: Mitochondria are popularly called the “powerhouses” of the cell. They promote energy metabolism through the tricarboxylic acid (TCA) cycle and oxidative phosphorylation, which in contrast to cytosolic glycolysis are oxygen-dependent and significantly more substrate efficient. That is, mitochondrial metabolism provides substantially more cellular energy currency (ATP) per macronutrient metabolised. Enhancement of mitochondrial density and metabolism are associated with endurance training, which allows for the attainment of high relative VO2 max values. However, the sedentary lifestyle and diet currently predominant in the Western world lead to mitochondrial dysfunction. Underdeveloped mitochondrial metabolism leads to nutrient-induced reducing pressure caused by energy surplus, as reduced nicotinamide adenine dinucleotide (NADH)-mediated high − electron flow at rest leads to “electron leak” and a chronic generation of superoxide radicals (O2 ). Chronic overload of these reactive oxygen species (ROS) damages cell components such as DNA, cell membranes, and proteins. Counterintuitively, transiently generated ROS during exercise contributes to adaptive reduction-oxidation (REDOX) signalling through the process -

Carbohydrate Recommendations for Marathon Runners
Carbohydrate Recommendations for Marathon Runners By: Alison Osowski Introduction arathon running is common all around 1. ING New York City Marathon, New York the world. There are many kinds of City, New York (43,660 finishers, average) Mmarathons, but running marathons are 2. Bank of America Chicago Marathon, Chicago, Illinois (33,701 finishers, average) the most common. A full running marathon 3. Boston Marathon, Boston, Massachusetts consists of running 26.2 miles along a course, (22,843 finishers, average) often through a city or other trail. The average 4. Marine Corps Marathon, Washington, D.C. time for a male runner in 2013 was 4 hours 16 (21,405 finishers, average) minutes (9:46/mile pace) compared to the 5. Honolulu Marathon, Honolulu, Hawaii average for females at 4 hours 41 minutes (20,323 finishers, average) (10:43/mile pace) (Running USA, 2014). The 6. Walt Disney World Marathon, Orlando, men’s record for the fastest marathon ran to date Florida (14,948 finishers average) was completed at the 2011 Boston Marathon by 7. Los Angeles Marathon, Los Angeles, Geoffrey Mutai with a time of 2:03:02 (roughly 4.7 California (14,125 finishers, average) minutes/mile), whereas the women’s record for 8. Rock ‘n’ Roll San Diego Marathon, San Diego California (13,391 finishers, average) the fastest marathon is 2:17:42 at the 2005 9. Medtronic Twin Cities Marathon, London Marathon (Running USA, 2014). Many Minneapolis, Minnesota (8,474 finishers, athletes also run half marathons, which consist of average) 13.1 miles and are usually along a shorter 10. -
Printable Version
Nutrition and Sport Topic 37 Module 37.1 Substrate utilization Katarina Melzer Learning objectives • Calculate energy expenditure during resting state; • Identify the size of the intramuscular ATP-CP pool for high intensity exercise; • Explain the influence of exercise intensity and duration on substrate utilization; • Describe the effect of training on substrate utilization. Contents 1. Substrate utilization during resting state 2. Anaerobic pathway for energy production 3. Aerobic pathway for energy production 4. Exercise intensity and substrate utilization 5. Exercise duration and substrate utilization 6. Effect of training on substrate utilization 7. Exercise mode and fat utilization 8. Summary Key messages • In a rested state, average person consumes about 3.5 ml of O2 per kilogram body weight per minute or 1 kcal per kg body weight per hour; • Physical activity is one of the means of significantly increasing the total energy expenditure above the resting metabolic rate in healthy subjects; • During light exercise, the required energy is provided almost exclusively by the aerobic system. As the intensity of exercise increases, the role of the anaerobic systems becomes more important; • During low intensity exercise, fat predominates as energy substrate, whereas during high intensity exercise, carbohydrate presents the major fuel for utilization; • The pattern of substrate utilization changes with time, even when the exercise intensity remains constant. The longer the time spent exercising, the higher the contribution of fat as an energy substrate. 2 1. Substrate utilization during resting state Resting metabolic rate (RMR) accounts for about 60-70% of total energy expenditure, the remainder being accounted for by diet induced thermogenesis (10%) and physical activity of the subjects (~20-30%) (Figure 1). -
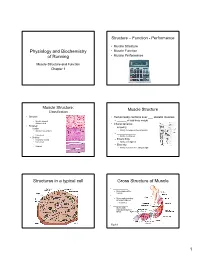
Physiology and Biochemistry of Running
Structure – Function - Performance • Muscle Structure Physiology and Biochemistry • Muscle Function of Running • Muscle Performance Muscle Structure and Function Chapter 1 Muscle Structure: Muscle Structure Classification •Smooth • Human body contains over ___ skeletal muscles • ____________________ • Spindle shaped – _______ of total body weight • Uninucleated • Characteristics •Striated – Irritability – Cardiac • Autonomous system • Ability to respond to a stimulus • ___________________ – ______________ • Cylindrical • Ability to shorten –Skeletal • Voluntary control – Extensibility • Cylindrical • Ability to lengthen • ____________________ – Elasticity • Striated • Ability to return to resting length Structures in a typical cell Gross Structure of Muscle • ___________ – Surrounds entire muscle • ___________ – Surrounds bundles of muscle fibers • Fascicles • ___________ – Surrounds individual muscle fibers Fig 8.1 1 • Sarcolemma: Muscle cell membrane • Myofibrils Threadlike strands within muscleMicrostructure fibers – ______________________ – ______________________ of Skeletal • Elastic tissue (proteins) –Sarcomere within the sarcomere. • Z-line, M-line, H-zone, A-band & I- – _____: extends from the bandMuscle Z-disc to the M-line. – Elastic in PEVK region • amino acids: proline, glutamate, valine, and lysine – ___________________ __________________. • Connective tissue related to fatigue? – Weight bearing vs. non- weight bearing. – “hitting the wall” Fig 8.2 Neuromuscular Junction • ______________________________________________________ -

Marathon & Beyond
Marathon & Beyond -- The web site for marathoners and ultrarunners. http://www.marathonandbeyond.com/choices/latta.htm Hitting "The Wall" by Sara Latta If You Understand the Scientific Reasons Behind “The Wall,” You Should Be Able to Avoid It. © 2003 42K(+) Press, Inc. "It felt like an elephant had jumped out of a tree onto my shoulders and was making me carry it the rest of the way in.”—Dick Beardsley, speaking of hitting "The Wall" at the second marathon of his career, the 1977 City of Lakes Marathon. “I wasn’t wanting to talk much. And when I’m not talking, you know I’m hurting.”—Don Frichtl, a runner who encountered "The Wall" somewhere after mile 21 of the 2002 Chicago Marathon. “At around mile 23, I was beginning to feel like the anchor was out.”—George Ringler, speaking of his 1991 Lake County Marathon. “The Wall.” It evades easy definition, but to borrow from Supreme Court Justice Potter Stewart’s famous definition of obscenity, you know it when you see it—or rather, hit it. It usually happens around mile 20, give or take a couple of miles. Your pace slows, sometimes considerably. Some runners say that it feels as though their legs had been filled with lead quail shot, like the stomach of Mark Twain’s unfortunate jumping frog of Calaveras County. Others can’t feel their feet at all. Thought processes become a little fuzzy. (“Mile 22, again? I thought I just passed mile 22!”) Muscle coordination goes out the window, and self-doubt casts a deep shadow over the soul.