DOCSLIB.ORG

A Review and Comparison of the Mathematics Gcse Syllabuses Offered for Examination in 1988

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Review and Comparison of the Mathematics Gcse Syllabuses Offered for Examination in 1988 A REVIEW AND COMPARISON OF THE MATHEMATICS GCSE SYLLABUSES OFFERED FOR EXAMINATION IN 1988 by PETER DAVID MORRIS B.Sc. A Master's Dissertation submitted in partial fulfilment of the requirements for the award of the degree of M.Sc. in Mathematical Education of the Loughborough University of Technology, 1988. Supervisor: Mr. P. K. Armstrong B.Sc. M.Sc. ~ by PETER DAVID MORRIS 1988 ABSTRACT In September 1986 the first groups of children began courses which will culminate in the award of the General Certificate of Secondary Education. From November 1987 (January 1988 in the case of London University Examinations) the General Certificate of Education and the Certificate of Secondary Education are no longer available. The Department of Education and Science and the Welsh Office have published GCSE: The National Criteria - General Criteria (9) in which the rules and regulations for the development of any GCSE courses are detailed. This includes a commitment to 'Criteria Referencing' as opposed to 'Norm Referencing' for the award of GCSE grades. The seven grades defined will eventually be awarded for reaching 'pre-determined standards of performance specific to the subject concerned'. The publication: GCSE: The National Criteria - Mathematics (10) sets out the essential requirements which must be satisfied by all syllabuses for examinations entitled 'Mathematics'. Within the criteria specified the Examining Groups are responsible for devising their own syllabuses and techniques for assessment. The Subject Criteria for Mathematics specifies fifteen ~ims' and seventeen 'Assessment Objectives' which should be adopted by syllabuses on offer. The mathematical content is defined by List 1 which has to be included in ~ syllabuses; by List 2 which has to be included in all syllabuses on which a candidate can be awarded a grade 'C'. Grades 'A' and 'B' will only be awarded to candidates who have completed a syllabus well in excess of that contained in List 1 and List 2. The dissertation studies the background to GCSE and the Subject Criteria specific to Mathematics. Methods of differentiation are discussed together with a general section concerning coursework. The main part of the the work details the schemes of assessment specified by the Examining Groups; each has submitted a scheme including a school based component and a scheme examined entirely by end of course written papers. In addition to these syllabuses the dissertation includes details of other nationally available schemes, namely SMP, KMP and MEI, together with all of the Mode 2 and Mode 3 syllabuses (none from LEAG and NEA). Schemes which are based. on 100% coursework are also reviewed:- ATM/SEG, MEG and GAIM (not available in 1988). Syllabuses which are undertaken in one year, usually on offer to 'mature' students, are also reViewed. The dissertation ends by posing questions about GCSE and Mathematics which have become prominent since its inception. ACKNOWLEDGEMENTS I would like to express my thanks to the following people: My tutor, Hr Peter Armstrong, for his invaluable help, 8lidance and constructive critism during the writing of this dissertation, my wife, Geraldine, who typed and corrected the manuscript and whose help was indispensible. DECLARATION I, Peter David Morris, declare that the contents of this dissertat1on, 'A Review and Compariscn of the Mathematics GCSE Syllabuses offered for Examination in 1988' are entirely my own work. CONTENTS Chapter Abstract 1. Introduction 1 2. The Mode 1 Syllabuses 12 3. Nationally Available Mcde 1 Syllabuses 26 4. Mode 2 Syllabuses 31 5. Mode 3 Syllabuses 39 6. Mature Syllabuses 51 7. Other Schemes 56 8. Conclusion 66 Bibliography 75 Appendices 78 CHAPTER 1 Introduction 1 1.1 General Introduction. The summer of 1988 will see the first staging of a single system of examining pupils at 16+. The G.C.E. O-level and C.S.E. examination dual system will be replaced by the General Certificate of Secondary Education (GCSE). The main aims of the GCSE are: to improve the quality of education to raise standards of attainment to produce a system that is fairer to candidates to motivate teachers and pupils to enhance the esteem in which examinations are held to promote improvements in the secondary school curriculum to remove the need for schools to enter candidates for O-level and C.S.E. in the same subject.' (8) The GCSE is to be administered by six Examining Groups: The London and East Anglian Group (L.E.A.G.) The Midland Examining Group (M.E.G.) The Northern Examining Association (N.E.A.) The Southern Examining Group (S.E.G.) The Welsh Joint Education Committee (W.J.E.C.) The Northern Ireland Schools Examinations Council (N.I.E.C.) The Examining Group's work is to be monitored by the Secondary Examinations Council (S.E.C.) and in particular the S.E.C. have the right to sanction or veto any syllabuses submitted according to whether the National Criteria and the 2 Subject Specific Criteria have been followed. The Examining Groups have to abide by the National Criteria, published in March 1985, when they are :- drawing up examination syllabuses devising assessment procedures conducting examinations awarding grades and issuing certificates. The National Criteria are set out in two parts, General and Subject Specific. 1. The General Criteria set out rules and procedures which govern the practices of the Examining Groups over all assessment matters. The General Criteria lay down guidelines for all syllabuses in all subjects. 2. The Subject Specific Criteria determine a framework for each of twenty (approximately 85% of total entries are made in these) subjects in terms of aims, objectives, content and assessment procedures. The change from the dual system of G.C.E. and C.S.E •• to the single system of GCSE has been prompted for a variety of reasons which the aims of the GCSE mirror. A criticism aimed at a Joint 'a' level and C.S.E. system concerns the proliferation of examination titles and syllabuses, the number of which has increased year by year. The Examining Boards, of which there are 20, had by 1984 developed almost 20,000 different syllabusus. It was not unusual for neighbouring schools to have been undertaking different syllabuses in mathematics. Many schools were also dealing with many different Examining Boards because different departments would be attracted 3 to syllabuses from different boards for a variety of reasons. Confusion was apparent amongst pupils, teachers, parents and employers. Difficulties arose when pupils transferred schools and employers found difficulty in understanding why one syllabus would include an item which they considered important whereas pupils from another local school, following a different syllabus, would not have covered the same ground. 1.2 The Need for Change. The majority of schools are now comprehensive and it seems logical for all comprehensives schools to follow a single examination system. The '0' level, introduced in 1951, was aimed at the population who attended grammar schools although many pupils who entered secondary modern schools gained considerable success in the examination. The C.S.E. examinations, introduced in 1965, were meant to be nationally available for all pupils and the 'average' attainment target was grade 4 with grade 1 being perceived as equivalent to a G.C.E. '0' level grade C. Many people, parents, pupils, teachers and employers never really gave the C.S.E. examination the credit it was due. Quite often it was more difficult to achieve a grade 1 at C.S.E. than it was to achieve a grade C at '0' level in the same subject. C.S.E. examinations also introduced the idea of coursework in examinations so that the final grade awarded did not rest on the candidates performance. in one or two final timed written examination papers. The performance of a pupil over an extended 4 period, usually two years, was assessed. However, in mathematics, coursework was often a misnomer. , Coursework , consisted of a series of timed written, formal tests. Pupils who were neither truly '0' level standard or truly C.S.E. standard were placed in the difficult position, as were the teachers, of having to enter two examinations. More often than not they would be expected to follow an '0' level course in preparation for both '0' level and C.S.E. examinations. A single system of examinations, therefore, with a seven point (eight really if. one includes ungraded) attainment scheme should cater for the majority of pupils in a comprehensive school. 1.3 GCSE and Mathematics. In the introduction to The National Criteria for Mathematics (10) it states that the 'criteria should be so interpreted that any scheme of assessment will:- (1) assess not only the performance of skills and techniques but also pupils understanding of mathematical processes in the solution of problems and their ability to reason ma thematically; (ii) offer differentiated examination papers so that, by choosing papers at an appropriate level, pupils are enabled to demonstrate what they know and can do rather than what they cannot do; (iii) encourage and support the provision of courses which enable pupils to develop their knowledge and understanding of mathematics to the full extent of their capabilities, to have 5 experience of mathematics as a means of solving practical problems and to develop confidence in their use of mathematics; (iv) have regard to the need for examination tasks to relate, where appropriate, to the use of mathematics in everyday situations.' The National Criteria of Mathematics document lays down fifteen Aims (see Appendix A) and seventeen Assessment Objectives (see Appendix B). The Syllabus Content is divided into List 1 and List 2 (see Appendix C). The content of List 1 has to be included in all syllabuses called Mathematics and candidates expected to achieve grades E,F,G will not be expected to know more.
Load more

Recommended publications
  • Guidance on Examinations
    EXAMINATION INFORMATION Qualifications The internal assessment component of many standard qualifications and courses, such as National Vocational Qualifications and GCSE’s can restrict the choice of qualifications which home educated children may wish to aspire to. Likewise GCSE qualifications are not offered or centrally organised by one examinations board. There are a number of different examination boards and each offers a variety of syllabuses. It is crucial therefore that if you wish your child to sit GCSE examinations; before embarking him/her on a particular course, you should first ensure that you identify a centre such as a school or college, which will accept his/her examination entry. In such circumstances you may find it helpful to consider the following procedures: If you have an existing and positive relationship with a school or college you may wish to enquire as to whether your child could be entered there for the exams you wish him/her to sit. At the same time you should ensure that the school or college would be willing to undertake to assess any coursework. If you do not have a relationship or contact with a school or college, you will need to contact an examinations board, which should be able to arrange a local centre on your behalf. If you do this you should also ensure that the board could arrange for any coursework to be assessed. In either case you should ensure that you know and have a copy of the exact syllabus to be studied for that year. Examinations boards can supply syllabuses and copies of previous exam papers at nominal cost.
    [Show full text]
  • Obtaining Exam Results
    Past exam certificates JMHS does not hold records of students' individual awards nor does it retain any copies of past certificates. To obtain copies of past certificates, you would need to contact the relevant awarding bodies. There are now five main awarding bodies for these qualifications operating in England, Wales and Northern Ireland. Please consult the list below to see who may now have a copy of your past certificate: Old Exam Title New Awarding Body Board AEB Associated Examinations AQA (Guildford) Board Tel - Switchboard: 01483 506506 - ask for Candidates Services Records SEG Southern Examining Group Email: [email protected] Fax: 01483 455731 SEREB South East Regional Examinations Board SWExB South Western (Regional) Examinations Board ALSEB Associated Lancashire AQA (Manchester) Schools Examining Board Tel - Exam Records : 0161 953 1180 - ask for Candidates Services Records JMB Joint Matriculation Board Email: [email protected] Fax: 0161 4555 444 NEA Northern Examining Association NEAB Northern Examinations and Assessment Board NREB North Regional Examining Board NWREB North Western Regional Examining Board TWYLREB The West Yorkshire and Lindsey Regional Examinations Board YHREB Yorkshire and Humberside Regional Examinations Board NISEAC Northern Ireland School CCEA Examinations and Assessment Council Download form from the CCEA website , print out and send in hard copy, or NISEC Northern Ireland School Examinations Council Request form - asking for Exam Support - by: Post Tel - Exam Support: 02890 261200 Email:
    [Show full text]
  • Work out Accounting GCSE the Titles in This Series0
    MACMILLAN WORKOUT SERIES Work Out Accounting GCSE The titles in this series0 For examinations at 16+ Accounting Human Biology Biology Mathematics Chemistry Numeracy Computer Studies Physics Economics Sociology English Spanish French Statistics German For examinations at 'A' level Applied Mathematics Physics Biology Pure Mathematics Chemistry Statistics English Literature For examinations at college level Dynamics Operational Research Elements of Banking Engineering Thermodynamics Mathematics for Economists MACMILLAN WORKOUT SERIES P. Stevens M MACMILLAN © P. Stevens 1986, 1987 All rights reserved. No reproduction, copy or transmission of this publication may be made without written permission. No paragraph of this publication may be reproduced, copied or transmitted save with written permission or in accordance with the provisions of the Copyright Act 1956 (as amended). Any person who does any unauthorised act in relation to this publication may be liable to criminal prosecution and civil claims for damages. First published 1986 Reprinted with corrections 1986 (twice) This edition 1987 Published by MACMILLAN EDUCATION LTD Houndmills, Basingstoke, Hampshire RG21 2XS and London Companies and representatives throughout the world Typeset by TecSet Ltd, Wallington, Surrey British Library Cataloguing in Publication Data Stevens, P. Work out accounting GCSE.-2nd ed.­ (Macmillan work out series) 1. Accounting-Examinations, questions, etc. I. Title II. Stevens, P. Work out principles of accounts 657'.076 HF5661 ISBN 978-0-333-44012-4 ISBN 978-1-349-09460-8
    [Show full text]
  • Marketing Fragment 6 X 10.T65
    Cambridge University Press 978-0-521-88414-3 - Examining the World: A History of the University of Cambridge Local Examinations Syndicate Edited by Sandra Raban Index More information Index Abingdon Junior Certificate Examination, 126 John Mason High School, 85 Ministry of Education, 126 Adeyinka, A. A., 117 Balfour Education Act, 53 Advanced International Certificate of Barbados, 57 Education (AICE), 115 Bardell, G. S., 170 Advanced Vocational Certificate of Bateson, W. H., 21 Education, 100 BBC, 85 African dependencies, 61 Beaver, Mr, 161 Advisory Committee on Education in, Beck, 18 61 Belgium, 6 Alderson, Charles, 149 Belgian authorities, 69 Alpine Club, 17 Beloe Report, 92, 93 Argentina, 109, 122 Bennett, Sterndale, 14 Cambridge Examinations Committee, Bentham, Jeremy, 40 122 Binet, Alfred, 63 Ashley-cum-Silverley, Cambridgeshire, 17 Biomedical Admissions Test (BMAT), 178 Associated Examining Board (AEB), 82, Birmingham, 36, 37 86, 101, 123 University, 60 Association for Headmistresses, 21 Bissoondoyal, Surendra, 114 Association for Science Education, 84 Black, Michael, 26 Association of Assistant Masters and Board of Education, 53, 54, 59, 60, 71, 73, Assistant Mistresses of Private 75, 76, 163, 164 Schools, 21 President, 71 Association of Recognised English Proposals for Examinations, 163 Language Schools (ARELS), 156 Botswana, 110, 116, 119 Associations for Headmasters and Brereton, Joseph Lloyd, Secretary of the Headmistresses, 21 Syndicate, 7, 19, 27, 60, 66, 75, 109, Atkinson, Hon. Mrs, 15 110, 166, 182 Attwood, John, 121 Brighton, 36, 44 Australia, 150 Bristol, 36, 44 Avery Hill and Bristol Project for Bishop of, 17 Geography, 176 British Academy, 17 British Council, 7, 116, 122, 144, 149, 150, Bachman, L.
    [Show full text]
  • I've Lost My Examination Certificates, Where Can I Get Hold of Copies?
    I’ve lost my examination certificates, where can I get hold of copies? Contact the exam boards directly for replacement certificates, using the links below for further information: AQA - http://www.aqa.org.uk/contact-us/past-results-and-lost-certificates OCR - http://www.ocr.org.uk/students/lost-or-incorrect-certificates/ WJEC - http://www.wjec.co.uk/students/certificates/ Pearson / Edexcel - https://qualifications.pearson.com/en/support/Services/replacement- certificates.html Over the past twenty years a number of examination boards have merged. If you are not sure which board/s you took your examinations with or how to contact them please see the document produced by Ofqual at http://www.ofqual.gov.uk/help-and-support/94-articles/264- getting-copies-of-exam-certificates this shows how examination boards merged to form the current awarding bodies. If you still cannot remember which board/s you took your examinations with you can contact the various awarding bodies to see if they have a record of you achieving a qualification with them. If they cannot find a record of your qualification with them and therefore cannot issue confirmation they will not make any charge. Please note that there is generally a charge for issuing confirmation of qualifications and you will need to be able to prove that you are the certificate holder. If your old exam board no longer exists Check which board to contact for a replacement certificate or certified statement of results if your old board no longer exists. AQA (Education) Contact AQA if your old exam
    [Show full text]
  • The English Examining Boards: Their Route from Independence to Government Outsourcing Agencies
    The English Examining Boards: Their route from independence to government outsourcing agencies Janet Sturgis Institute ofEducation Thesis submitted in fulfilment of the requirements of the Degree of Doctor of Philosophy of the University of London Abstract The contention of this thesis is that the independent English examining boards have been gradually transformed from independent organisations administering a national qualifications system to virtual outsourcing agencies working within a centrally controlled framework. The thesis begins with a review of the literature of English education which reveals that within that literature the examining boards have remained peripheral bodies, accepted as an element in the secondary assessment structure but never seriously analysed. Within a theoretical framework based on the central concept of the encroaching "managerial state", this absence has informed the methodology, which locates the university examining boards as the focus in a historical narrative of the development ofthe unique English post-16 qualifications providers. The central section of the thesis concentrates on the examining boards in the 1990s, and suggests that the pressures of that decade threatened their stability. Data in support of the analysis of this section was gathered in a series of interviews with significant actors from the boards and their regulatory agencies. Then a section dealing with the A-level grades crisis of September 2002 suggests that this event provides clear evidence ofthe Boards' loss ofprofessional independence. The thesis concludes that the English examining boards can no longer be deemed independent and ends with some observations on the significance of this change with two possible directions suggested for their future.
    [Show full text]
  • 2 a Brief History of Policies, Practices and Issues
    QCAChap2CB:QCAchap2CB 11/12/2007 17:16 Page 43 Techniques for monitoring the comparability of examination standards, edited by: Paul Newton, Jo-Anne Baird, Harvey Goldstein, Helen Patrick and Peter Tymms 2 A BRIEF HISTORY OF POLICIES, PRACTICES AND ISSUES RELATING TO COMPARABILITY Kathleen Tattersall Abstract This chapter which describes developments in education and assessment in England from the mid 19th century to the present day is in three parts: 1. the emergence of a ‘national system’ (the 1850s to the end of the Second World War) 2. the development and expansion of the system (1945 to the 1990s) 3. the emergence of a regulated system from the 1990s onwards. The role of comparability at each stage of these developments is highlighted. 1 An emerging national system of education and examinations 1.1 Overview Comparability is a fundamental requirement of England’s assessment system: between providers of the same product, qualifications, subjects, the demands of tests and tasks, between assessor judgements of students’ work and across time. Comparability is also an essential element of England’s accountability methodology and is expected to guarantee to governments, the general public, students and selectors that assessment is fair, equitable and reliable. Without assurances of equivalence between different instruments and outcomes that are used to make selections for jobs or a university place or to aid future learning, the basis of decision- making is flawed. The more intense the competition for work, places on courses or financial reward, the more intense is the pressure on the assessment system to demonstrate the steps taken to assure comparability.
    [Show full text]
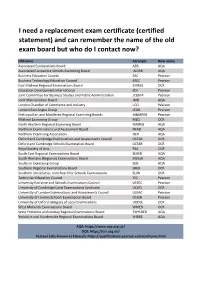
  • Old Exam Board Names.Xlsx
    I need a replacement exam certificate (certified statement) and can remember the name of the old exam board but who do I contact now? Old name Acronym New name Associated Examinations Board AEB AQA Associated Lancashire Schools Examining Board ALSEB AQA Business Education Council BEC Pearson Business Technology Education Council BTEC Pearson East Midland Regional Examinations Board EMREB OCR Education Development International EDI Pearson Joint Committee for Business Studies and Public Administration JCBSPA Pearson Joint Matriculation Board JMB AQA London Chamber of Commerce and Industry LCCI Pearson London East Anglia Group LEAG Pearson Metropolitan and Middlesex Regional Examining Baords M&MREB Pearson Midland Examining Group MEG OCR North Western Regional Examining Board NWREB AQA Northern Examinations and Assessment Board NEAB AQA Northern Examining Association NEA AQA Oxford and Cambridge Examinations and Assessments Council OCEAC OCR Oxford and Cambridge Schools Examination Board OCSEB OCR Royal Society of Arts RSA OCR South East Regional Examinations Board SEREB AQA South Western (Regional) Examinations Board SWExB AQA Southern Examining Group SEG AQA Southern Regional Examinations Board SREB OCR Southern Universities Joint Board for Schools Examinations SUJB OCR Technician Education Council TEC Pearson University Entrance and Schools Examinations Council UESEC Pearson University of Cambridge Local Examinations Syndicate UCLES OCR University of London Examinations and Assessments Council ULEAC Pearson University of London Schools Examination Board ULSEB Pearson University of Oxford Delegacy of Local Examinations UODLE OCR West Midlands Examinations Board WMEB OCR West Yorkshire and Lindsey Regional Examinations Board TWYLREB AQA Yorkshire and Humberside Regional Examinations Board YHREB AQA AQA: https://www.aqa.org.uk/ OCR: https://ocr.org.uk/ Pearson (also known as Edexcel): https://qualifications.pearson.com/en/home.html.
    [Show full text]
  • Get a Replacement Exam Certificate
    GOV.UK 1. Home (https://www.gov.uk/) 2. Education and learning (https://www.gov.uk/browse/education) 3. Apprenticeships, 14 to 19 education and training for work (https://www.gov.uk/browse/education/find-course) Get a replacement exam certificate 1. Who to contact Contact an exam board to get a replacement exam certificate or certified statement of results. You cannot get a replacement certificate for an O level, CSE, GCSE or A level - your exam board will send you a ‘certified statement of results’ instead. You can use this in place of your exam certificate, for example for a university application. Boards may give you a replacement certificate for other qualifications they offer. You may need to prove your identity and pay a fee. Find out which exam board you should contact if your old exam board no longer exists (https://www.gov.uk/replacement-exam-certificate/if-your-old-exam-board-no- longer-exists). Check with your school or college if you’re not sure which exam board holds your results. Exam boards The 5 boards in England, Wales and Northern Ireland are: Assessment and Qualifications Alliance (AQA) (https://www.aqa.org.uk/contact-us/past-results-and-lost-certificates) Council for Curriculum and Examinations Assessment (CCEA) (http://ccea.org.uk/qualifications/adminhelp/replacement_certificates) Pearson Edexcel (http://qualifications.pearson.com/en/support/Services/replacement-certificates.html) Oxford, Cambridge and RSA Exams (OCR) (http://www.ocr.org.uk/ocr-for/learners-and-parents/lost-or-incorrect-certificates/) Welsh Joint Examinations Committee (WJEC) (http://www.wjec.co.uk/students/certificates/) Contact the Scottish Qualifications Authority (SQA) (http://www.sqa.org.uk/sqa/212.html) for replacement certificates for Scottish qualifications.
    [Show full text]
  • The Five-Decade Challenge a Wake-Up Call for UK Science Education? November 2008
    The Five-Decade Challenge A wake-up call for UK science education? November 2008 www.rsc.org Foreword During the coming decades, chemistry will be key in addressing global issues relating to energy, food, water, the environment, health and overall sustainability. If the subject is to retain its strong scientific research base in the UK, and benefit from innovation throughout the industrial and other commercial sectors, it is essential that this country’s education system can provide both science graduates and a broader technically-literate society with the relevant knowledge and skills. Industrialists and senior academics are placing increasing priority on problem-solving and strong mathematical abilities, rather than the mere recalling of facts or simplistic analysis within well-defined boundaries of experience.1 This follows from the extraordinary and rapid proliferation of information globally, which means that success goes to those who can most readily analyse and deliver in unfamiliar, complex or uncertain business and technological environments.2 Over the last five decades, the national examinations set for 16 year-olds in science in England, Wales and Northern Ireland have changed markedly, from the General Certificate of Education (GCE) Ordinary Level (O-level) system of the 1960s, 1970s and 1980s, which was set for more able pupils and ran in parallel to the Certificate of Secondary Education (CSE), to the broadly based framework of the General Certificate of Secondary Education (GCSE) through the 1990s and this decade. Within this arrangement, there have been many changes over time to the criteria set by the Qualifications and Curriculum Authority (QCA) and specifications (syllabuses) derived by five competing Awarding Bodies that manage the assessment process.
    [Show full text]
  • Work out Mathematics GCSE MACMILLAN WORKOUT SERIES
    MACMILLAN MASTER SERIES Work Out Mathematics GCSE MACMILLAN WORKOUT SERIES G.D. Buckwell M MACMILLAN The titles in this. series For examinations at 16+ Accounting Human Biology Biology Mathematics Chemistry Numeracy Computer Studies Physics Economics Sociology English Spanish French Statistics German For examinations at A' level Applied Mathematics Physics Biology Pure Mathematics Chemistry Statistics English Literature For examinations at college level Dynamics Operational Research Elements of Banking Engineering Thermodynamics Mathematics for Economists © G. D. Buckwell 1986, 1987 All rights reserved. No reproduction, copy or transmission of this publication may be made without written permission. No paragraph of this publication may be reproduced, copied or transmitted save with written permission or in accordance with the provisions of the Copyright Act 1956 (as amended). Any person who does any unauthorised act in relation to this publication may be liable to criminal prosecution and civil claims for damages. First published 1986 Reprinted 1986 Reprinted (with corrections) 1986 This edition 1987 Published by MACMILLAN EDUCATION LTD Houndmills, Basingstoke, Hampshire RG2l 2XS and London Companies and representatives throughout the world Typeset by TecSet Ltd, Wallington, Surrey Printed and bound in Great Britain by Scotprint Ltd., Musselburgh, Scotland British Library Cataloguing in Publication Data Buckwell, G. D. (Macmillan work out series) 1. Mathematics-Examinations, questions, etc. I. Title 510'.76 QA43 ISBN 978-0-333-44013-1
    [Show full text]
  • GOOD DESIGN TOHELP YOU ... Reaigcseq~E~S~T:Io:N:S~ ___
    GOOD DESIGN Diagrams of useful or difficult ideas Topic guide shows Subheads break TOHELP you what's covered content into YOU ... in each chapter manageable bits Topic Guide """-....._ \..1_ .....: .. _ ... ....- .............__ ~.-."" •___ ...... .. 0..,....1. -.- ..I,......., ... ~'- (ot)... _C6 -'--"'hI,,-. ___ ...... _ ....... .-.-1 ••,. .... dt., ... --.-·............ ,...., " _ __ IQ~o.- ........__ ~~ dr r..... lJ.. .,'Iot~...... ==.. o--.In. ..................__ .... #...--.... ............ .,..........-. ~ .........."" .. """ .... ___...... .. .or._~.. Digestion ..... --..,.. ,..... ..................... .............Iooor........ eoI_ ........ _ ... -_ ................ - .... --.-'.. ...",.,...--.. .»-_ .. ""' .......... _ _.... ---_..... ............................ -.......,.-.1....... ........"""---.. .... "'" n....~.. _.,,.. .. __ 'II...... ... ....................... ...-..- .. -~'-_ ........... The key facts for ......... _ ........ n. ...,--_ ............, .. _ _ ----~+1~---------------------- ~~~~~~~M~=-....., lit .......~_ ..._ 0 ..1,.... 1_'-.1 ,... "'--'..... ....,- .......,.. - .........._... ~ ...... the exam DIGESTION ......-"" ....... ...uoI_ --......... ...'-........_ - .. ....-1..,.... .. ... __. 4'1 ~"~ -' .... ..........--""'0..- •• AND -"-.......... - ..... - ...................... ~ """'... _"' .... .. -' - 1M.... ABSORPTION ._ ....t ...""_., ......_ ...............~ 7he CirculatOf)' System .......... r~_ ... ..-.. otw..... ,.., , --,.,..., ....... ,.. _ _ 111 _ "':'.::.~~!~--.. - .... ....-. ...... __ .............
    [Show full text]