Implementation of Skeletal Muscle Model with Advanced Activation Control H
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Muscular System
THE MUSCULAR SYSTEM Muscles, the specialized tissues that facilitate body movement, make up about 40% of body weight. Most body muscle is the voluntary type, called skeletal muscle because it is attached to the bony skeleton. Skeletal muscle contributes to body contours and shape, and it composes the organ system called the mus cular system. These muscles allow you to grin, frown, run, swim, shake hands, swing a hammer, and to otherwise manipulate your environment. The balance of body muscle is smooth and cardiac muscles, which form the bulk of the walls of hollow organs and the heart. Smooth and cardiac muscles are involved in the transport of materials within the body. Study activities in this chapter deal with microscopic and gross structure of muscle, identification of voluntary muscles, body movements, and important understandings of muscle physiology. OVERVIEW OF MUSCLE TISSUES 1. Nine characteristics of muscle tissue are listed below and on page 104. Identify the muscle tissue type described by choosing the correct response(s) from the key choices. Enter the appropriate term(s) or letter(s) of the key choice in the answer blank. Key Choices A. Cardiac B. Smooth C. Skeletal 1. Involuntary 2. Banded appearance 3. Longitudinally and circularly arranged layers 4. Dense connective tissue packaging 5. Figure-8 packaging of the cells 6. Coordinated activity to act as a pump 103 1 04 Anatomy & Physiology Coloring Workbook 7. Moves bones and the facial skin 8. Referred to as the muscular system 9. Voluntary 2. Identify the type of muscle in each of the illustrations in Figure 6-1. -

Reviewing Morphology of Quadriceps Femoris Muscle
Review article http://dx.doi.org/10.4322/jms.053513 Reviewing morphology of Quadriceps femoris muscle CHAVAN, S. K.* and WABALE, R. N. Department of Anatomy, Rural Medical College, Pravara Institute of Medical Sciences, At.post: Loni- 413736, Tal.: Rahata, Ahmednagar, India. *E-mail: [email protected] Abstract Purpose: Quadriceps is composite muscle of four portions rectus femoris, vastus intermedius, vastus medialis and vatus lateralis. It is inserted into patella through common tendon with three layered arrangement rectus femoris superficially, vastus lateralis and vatus medialis in the intermediate layer and vatus intermedius deep to it. Most literatures do not take into account its complex and variable morphology while describing the extensor mechanism of knee, and wide functional role it plays in stability of knee joint. It has been widely studied clinically, mainly individually in foreign context, but little attempt has been made to look into morphology of quadriceps group. The diverse functional aspect of quadriceps group, and the gap in the literature on morphological aspect particularly in our region what prompted us to review detail morphology of this group. Method: Study consisted dissection of 40 lower limbs (20 rights and 20 left) from 20 embalmed cadavers from Department of Anatomy Rural Medical College, PIMS Loni, Ahmednagar (M) India. Results: Rectus femoris was a separate entity in all the cases. Vastus medialis as well as vastus lateralis found to have two parts, as oblique and longus. Quadriceps group had variability in fusion between members of the group. The extent of fusion also varied greatly. The laminar arrangement of Quadriceps group found as bilaminar or trilaminar. -
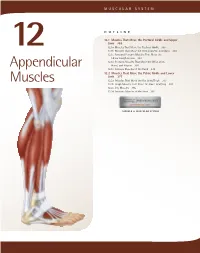
Appendicular Muscles 355
MUSCULAR SYSTEM OUTLINE 12.1 Muscles That Move the Pectoral Girdle and Upper Limb 355 12.1a Muscles That Move the Pectoral Girdle 355 12 12.1b Muscles That Move the Glenohumeral Joint/Arm 360 12.1c Arm and Forearm Muscles That Move the Elbow Joint/Forearm 363 12.1d Forearm Muscles That Move the Wrist Joint, Appendicular Hand, and Fingers 366 12.1e Intrinsic Muscles of the Hand 374 12.2 Muscles That Move the Pelvic Girdle and Lower Limb 377 Muscles 12.2a Muscles That Move the Hip Joint/Thigh 377 12.2b Thigh Muscles That Move the Knee Joint/Leg 381 12.2c Leg Muscles 385 12.2d Intrinsic Muscles of the Foot 391 MODULE 6: MUSCULAR SYSTEM mck78097_ch12_354-396.indd 354 2/14/11 3:25 PM Chapter Twelve Appendicular Muscles 355 he appendicular muscles control the movements of the upper 2. Identify the muscles that move the scapula and their actions. T and lower limbs, and stabilize and control the movements 3. Name the muscles of the glenohumeral joint, and explain of the pectoral and pelvic girdles. These muscles are organized how each moves the humerus. into groups based on their location in the body or the part of 4. Locate and name the muscles that move the elbow joint. the skeleton they move. Beyond their individual activities, these 5. Identify the muscles of the forearm, wrist joint, fingers, muscles also work in groups that are either synergistic or antago- and thumb. nistic. Refer to figure 10.14 to review how muscles are named, and Muscles that move the pectoral girdle and upper limbs are recall the first Study Tip! from chapter 11 that gives suggestions organized into specific groups: (1) muscles that move the pectoral for learning the muscles. -

Muscle Contributions to Knee Joint Stability: Effects of ACL Injury and Knee Brace Use
University of Windsor Scholarship at UWindsor Electronic Theses and Dissertations Theses, Dissertations, and Major Papers 1-1-2006 Muscle contributions to knee joint stability: Effects of ACL injury and knee brace use. Aaron Derouin University of Windsor Follow this and additional works at: https://scholar.uwindsor.ca/etd Recommended Citation Derouin, Aaron, "Muscle contributions to knee joint stability: Effects of ACL injury and knee brace use." (2006). Electronic Theses and Dissertations. 6943. https://scholar.uwindsor.ca/etd/6943 This online database contains the full-text of PhD dissertations and Masters’ theses of University of Windsor students from 1954 forward. These documents are made available for personal study and research purposes only, in accordance with the Canadian Copyright Act and the Creative Commons license—CC BY-NC-ND (Attribution, Non-Commercial, No Derivative Works). Under this license, works must always be attributed to the copyright holder (original author), cannot be used for any commercial purposes, and may not be altered. Any other use would require the permission of the copyright holder. Students may inquire about withdrawing their dissertation and/or thesis from this database. For additional inquiries, please contact the repository administrator via email ([email protected]) or by telephone at 519-253-3000ext. 3208. MUSCLE CONTRIBUTIONS TO KNEE JOINT STABILITY: EFFECTS OF ACL INJURY AND KNEE BRACE USE by Aaron Derouin A Thesis Submitted to the Faculty of Graduate Studies and Research through Kinesiology in Partial Fulfillment of the Requirements for the Degree of Master of Human Kinetics at the University of Windsor Windsor, Ontario, Canada 2006 © 2006 Aaron Derouin Reproduced with permission of the copyright owner. -
The Concise Book of Trigger Points Second Edition
The Concise Book of Trigger Points second edition Simeon Niel-Asher Lotus Publishing Chichester, England North Atlantic Books Berkeley, California Copyright © 2005, 2008 by Simeon Niel-Asher. All rights reserved. No portion of this book, except for brief review, may be reproduced, stored in a retrieval system, or transmitted in any form or by any means - electronic, mechanical, photocopying, recording, or otherwise - without the written permission of the publisher. For information, contact Lotus Publishing or North Atlantic Books. First published in 2005. This second edition published in 2008 by Lotus Publishing 3 Chapel Street, Chichester, P019 1BU and North Atlantic Books P O Box 12327 Berkeley, California 94712 All Drawings Amanda Williams Text Design Wendy Craig Models Jonathan Berry, Galina Asher Photography Sean Marcus Cover Design Paula Morrison Printed and Bound in Singapore by Tien Wah Press The Concise Book of Trigger Points is sponsored by the Society for the Study of Native Arts and Sciences, a nonprofit educational corporation whose goals are to develop an educational and crosscultural perspective linking various scientific, social, and artistic fields; to nurture a holistic view of arts, sciences, humanities, and healing; and to publish and distribute literature on the relationship of mind, body, and nature. Dedication To my parents, my wife Galina, for her support, beauty and wisdom, my wonderful patients and my sons Gideon and Benjamin who make every day an adventure. British Library Cataloguing in Publication Data A CIP record for this book is available from the British Library ISBN 978 1 905367 12 2 (Lotus Publishing) ISBN 978 1 55643 745 8 (North Atlantic Books) The Library of Congress has cataloged the first edition as follows: Niel-Asher, Simeon. -

Multiscale Modeling of Skeletal Muscle Tissues Based on Analytical and Numerical Homogenization
Multiscale modeling of skeletal muscle tissues based on analytical and numerical homogenization L.A. Spyroua,∗, S. Brisardb, K. Danasc aBiomechanics Group, Institute for Bio-Economy & Agri-Technology, Centre for Research & Technology Hellas (CERTH), 38333 Volos, Greece bUniversit´eParis-Est, Laboratoire Navier, UMR 8205, CNRS, ENPC, IFSTTAR, F-77455 Marne-la-Vall´ee,France cLMS, CNRS, Ecole´ Polytechnique, 91128 Palaiseau, France Abstract A novel multiscale modeling framework for skeletal muscles based on analytical and numerical homogeniza- tion methods is presented to study the mechanical muscle response at finite strains under three-dimensional loading conditions. First an analytical microstructure-based constitutive model is developed and numerically implemented in a general purpose finite element program. The analytical model takes into account explicitly the volume fractions, the material properties, and the spatial distribution of muscle's constituents by using homogenization techniques to bridge the different length scales of the muscle structure. Next, a numerical homogenization model is developed using periodic eroded Voronoi tessellation to virtually represent skeletal muscle microstructures. The eroded Voronoi unit cells are then resolved by finite element simulations and are used to assess the analytical homogenization model. The material parameters of the analytical model are identified successfully by use of available experimental data. The analytical model is found to be in very good agreement with the numerical model for the full range of loadings, and a wide range of different volume fractions and heterogeneity contrasts between muscle's constituents. A qualitative application of the model on fusiform and pennate muscle structures shows its efficiency to examine the effect of muscle fiber concentration variations in an organ-scale model simulation. -

Section 1 Lower Limbs Mcqs 1) Tensor Fasciae Latae Is Supplied By
Section 1 Lower Limbs mcqs 1) Tensor fasciae latae is supplied by : a) anterior division of femoral nerve b) superior gluteal nerve c) nerve to vastus lateralis d) inferior gluteal nerve e) lateral femoral cutaneous nerve 2) Which structure is intrasynovial at the knee joint: a) oblique popliteal ligament b) tendon of popliteus c) medial and lateral menisci d) anterior cruciate ligament e) none of the above 3) The ‘screw-home’ movement in extension of the knee joint begins with tightening of the: a) anterior cruciate ligament b) oblique popliteal ligament c) medial collateral ligament d) lateral collateral ligament e) posterior cruciate ligament 4) Tibialis anterior: a) is supplied by the tibial nerve b) inserts into the second metatarsal bone c) is pierced by the posterior tibial artery d) tendon perforates the superior extensor retinaculum e) does not arise from the interosseous membrane 5) The adductor canal: a) contains the femoral artery and nerve b) ends distally in the adductor longus hiatus c) contains no muscular nerves d) has adductor longus forming the root e) always has the femoral artery lying between the saphenous nerve and the femoral vein 6) The great saphenous vein: a) joins the femoral vein above the inguinal ligament b) begins as the upward continuation of the lateral marginal vein of the foot c) travels with the saphenous nerve along its course d) runs behind the medial malleolus e) enters the femoral vein on its anteromedial side 7) Regarding the femoral artery: a) adductor magnus lies between it and the profunda -

Phrenic and Cervical Afferents Following Spinal Cord Injury
PHRENIC AND CERVICAL AFFERENTS FOLLOWING SPINAL CORD INJURY By JAYAKRISHNAN NAIR A DISSERTATION PRESENTED TO THE GRADUATE SCHOOL OF THE UNIVERSITY OF FLORIDA IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY UNIVERSITY OF FLORIDA 2016 © 2016 Jayakrishnan Nair To my patients who inspired me to study the remarkable ability of the nervous system to change and adapt itself, and my family for their constant support in this quest. ACKNOWLEDGMENTS This work would not be possible without the support and encouragement from a lot of people. First and foremost, I would like to thank my mentor Dr. David Fuller for accepting me as a student when I was left stranded in the middle of my PhD. I also thank him for having trust in my abilities and his constant encouragement and guidance to wade through some of my toughest times in the lab when experiments failed miserably for over a year. I was also fortunate to have a team of world expert on my PhD supervisory committee to steer my thesis in the right direction without wandering off too much from what I set out to investigate. I am proud that my committee had an all- star lineup with experts like Dr. Paul Davenport, a world authority in respiratory afferents, Dr. Paul Reier, revered veteran in spinal cord physiology, Dr. Danny Martin and Dr. Emily Fox with years of clinical research expertise, and Dr. David Baekey for his insightful expertise in cardiorespiratory integrative physiology. I also would like to thank Dr. Gordon Mitchell whose recent migration to University of Florida totally transformed the lab work/fun environment by bringing in high quality science and people along with him. -

2021 SEACSM Annual Meeting Program
2021 Annual Meeting Program Conference Information Schedule and Presentation Listing Abstracts February 18–19, 2021 1 SEACSM 2021 ANNUAL MEETING CONFERENCE INFORMATION Welcome to the 2021 Annual Meeting! We are pleased to present our 49th Annual Meeting and first virtual Annual Meeting this year! At a time when so many events have been postponed or cancelled, we are grateful that we are able to meet again this year. We are also thankful to our members for registering for the meeting, submitting their research, and volunteering to help organize the conference. Most of all, we appreciate your patience as we moved our meeting to a virtual platform. The conference consists of over 250 presentations including 218 posters, 6 review/symposia, 24 student award competition posters, 5 invited lectures, and 5 clinical case presentations in the Sports Medicine Physician Track program. We also have three special events: the Emily Haymes Mentoring “Breakfast”, the Biomechanics special interest group meeting, and the awards ceremony for the Student Award Poster Competition. Throughout the meeting, the virtual Graduate School Fair and Exhibit Hall will be open. We are hosting our meeting using the Symposium by ForagerOne platform. The conference will include posters, review/symposia, clinical case presentations, and invited lectures. Most presentations will be an online poster format, some of which include a short video explanation from the author, and a mechanism for engagement and discussion with attendees. Poster presentations and symposia will be available throughout the conference with scheduled sessions to interact with presenters. Invited lectures will be pre-recorded with live chat with presenters during those sessions. -

Multiscale Modeling of Skeletal Muscle Tissues Based on Analytical and Numerical Homogenization L.A
Multiscale modeling of skeletal muscle tissues based on analytical and numerical homogenization L.A. Spyrou, K. Danas, Sébastien Brisard To cite this version: L.A. Spyrou, K. Danas, Sébastien Brisard. Multiscale modeling of skeletal muscle tissues based on analytical and numerical homogenization. Journal of the mechanical behavior of biomedical materials, Elsevier, 2019, 10.1016/j.jmbbm.2018.12.030. hal-01965947 HAL Id: hal-01965947 https://hal-polytechnique.archives-ouvertes.fr/hal-01965947 Submitted on 27 Dec 2018 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Multiscale modeling of skeletal muscle tissues based on analytical and numerical homogenization L.A. Spyroua,∗, S. Brisardb, K. Danasc aBiomechanics Group, Institute for Bio-Economy & Agri-Technology, Centre for Research & Technology Hellas (CERTH), 38333 Volos, Greece bUniversit´eParis-Est, Laboratoire Navier, UMR 8205, CNRS, ENPC, IFSTTAR, F-77455 Marne-la-Vall´ee,France cLMS, CNRS, Ecole´ Polytechnique, 91128 Palaiseau, France Abstract A novel multiscale modeling framework for skeletal muscles based on analytical and numerical homogeniza- tion methods is presented to study the mechanical muscle response at finite strains under three-dimensional loading conditions. First an analytical microstructure-based constitutive model is developed and numerically implemented in a general purpose finite element program. -

“The Falcon's Perspective”
OVERUSE INJURIES IN ATHLETICS APPROACHING GROIN PAIN IN ATHLETICS “THE FALCON’S PERSPECTIVE” – Written by Adam Weir, Netherlands and Qatar, Andreas Serner, Qatar, Andrea Mosler, Australia and Zarko Vuckovic, Qatar Falah the falcon is the mascot of the Doha CLINICALLY RELEVANT ANATOMY OF THE Adductor longus has a proximal 2019 Athletics World Championships. GROIN attachment on the pubic bone8. Palpation Falcons are important in Qatari culture and Adductor-related groin pain (both acute of the proximal tendon can be performed are renowned for their exceptional vision, and long-standing) is by far the most easily and following the tendon proximally even in the dark. For many clinicians, groin common groin injury in athletes2–5, so we with your finger, you can find the insertion9. pain in athletes is considered as an area of will start by looking at the adductors in Recognizable injury pain on palpation is darkness that is difficult to navigate. It seems more detail. There are a number of different one of the key features of adductor-related sometimes that diagnosing in athletes with adductor muscles: adductor longus, adductor groin pain1. The proximal tendon continues groin pain is as challenging as qualifying for brevis, adductor magnus, gracilis, pectineus, superficially, with the lateral part of the the World Championship finals. and obturator externus. The vast majority of tendon transitioning intramuscularly at Doha not only hosts many major sporting groin injuries affect the adductor longus3,6 approximately 1-2.5 cm from the insertion events, but we also hosted the first World and being able to locate and examine this (Figure 1)10.