DOCSLIB.ORG

Session 15 FLOWS THROUGH NOZZLE Outline

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Session 15 FLOWS THROUGH NOZZLE Outline Session 15 FLOWS THROUGH NOZZLE Outline • Definition • Types of nozzle • Flow analysis • Ideal Gas Relationship • Mach Number and Speed of Sound • Isentropic flow of an ideal gas • De Laval nozzle • Nozzle efficiency • Calculation examples Definition Nozzle is a duct by flowing through which the velocity of a fluid increases at the expense of pressure drop. A duct which decreases the velocity of a fluid and causes a corresponding increase in pressure is called a diffuser Types of Nozzles There are three types of nozzles a. Convergent nozzle b. Divergent nozzle c. Convergent-divergent nozzle Flow Analysis • Incompressible flow • Compressible Flow The variation of fluid density for compressible flows requires attention to density and other fluid property relationships. The fluid equation of state, often unimportant for incompressible flows, is vital in the analysis of compressible flows. Also, temperature variations for compressible flows are usually significant and thus the energy equation is important. Curious phenomena can occur with compressible flows. Flow Analysis • For simplicity, the gas is assumed to be an ideal gas. • The gas flow is isentropic. • The gas flow is constant • The gas flow is along a straight line from gas inlet to exhaust gas exit • The gas flow behavior is compressible Ideal Gas Relationship The equation of state for an ideal gas is: For an ideal gas, internal energy, û is considered to be a function of temperature only Thus, Ideal Gas Relationship The fluid property enthalpy, ĥ is defined as Since for an ideal gas, enthalpy is a function of temperature only, the ideal gas specific heat at constant pressure, Cp can be expressed as And, Ideal Gas Relationship We see that changes in internal energy and enthalpy are related to changes in temperature by values of Cp and Cv. We turn our attention now to developing useful relationships for determining Cp and Cv Thus, Since, so, Ideal Gas Relationship For compressible flows, changes in the thermodynamic property entropy, s, are important. For any pure substance including ideal gases, the “first T ds equation” is where T is absolute temperature, s is entropy, is internal energy, p is absolute pressure, and is density If Cp and Cv are assumed to be constant for a given gas, can be integrated to get Ideal Gas Relationship The second law of thermodynamics requires that the adiabatic and frictionless flow of any fluid results in ds = 0. Constant entropy flow is called isentropic flow. For the isentropic flow of an ideal gas with constant and Thus, which is a useful relationship between temperature, density, and pressure for the isentropic flow of an ideal gas. We can conclude that Mach Number and Speed of Sound The Mach number is defined as the ratio of the value of the local flow velocity, V, to the local speed of sound, c. In other words, This discussion about pressure wave patterns suggests the following categories of fluid flow: 1. Incompressible flow: Ma ≤ 0.3. Unrestricted, nearly symmetrical and instantaneous pressure communication. 2. Compressible subsonic flow: 0.3 < Ma < 1. Unrestricted but noticeably asymmetrical pressure communication. 3. Compressible supersonic flow: Ma > 1. Formation of Mach wave; pressure communication restricted to zone of action. Mach Number and Speed of Sound When the continuity equation is applied to the flow through this control volume, the result is Mach Number and Speed of Sound We can also write, Neglecting the product dρ.dV, both being very small, ρdV = cdρ The momentum equation for the control volume gives, (p-(p+dρ))A = ρAc((c-dV)-c) so., we obtain Mach Number and Speed of Sound We learned earlier that, And thus, Thus for an ideal gas Isentropic flow of an ideal gas When fluid flows steadily through a conduit that has a flow cross-section area that varies with axial distance, the conservation of mass 1 continuity 2 equation And If we form the logarithm of both sides of the continuity equation the result is Isentropic flow of an ideal gas Differentiating results Since the flow being considered is isentropic, the speed of sound is related to variations of pressure with density, repeated here for convenience as combined with the definition of Mach number So Isentropic flow of an ideal gas To better understand why subsonic and supersonic duct flows are so different, this equation can be used Converging-diverging duct flow In the preceding section, we discussed the variation of density and velocity of the steady isentropic flow of an ideal gas through a variable area duct. We proceed now to develop equations that help us determine how other important flow properties vary in these flows. Converging-diverging duct flow We demonstrated that for the isentropic flow of an ideal gas The streamwise equation of motion for steady and frictionless flow can be expressed for an ideal gas as since the potential energy term, γ dz can be considered as being negligibly small in comparison with the other terms involved. Converging-diverging duct flow Consider the steady, one-dimensional, isentropic flow of an ideal gas with constant Cp and Cv through the converging-diverging nozzle of By using the ideal gas equation of state we obtain It is of interest to note that combining leads to results in Converging-diverging duct flow The definition of Mach number and the speed of sound relationship for ideal gases can be combined to yield We can also develop an equation for pressure variation. Since p/ρ =RT then we obtain Converging-diverging duct flow Combining leads to For density variation we consolidate to get Converging-diverging duct flow We have already used the stagnation state for which Ma = 0 as a reference condition. It will prove helpful to us to use the state associated with Ma = 1 and the same entropy level as the flowing fluid as another reference condition we shall call the critical state, denoted We can get a relationship for the critical temperature ratio, T*T0, by substituting Ma = 1. Thus, De Laval nozzle Its operation relies on the different properties of gases flowing at subsonic and supersonic speeds. The speed of a subsonic flow of gas will increase if the pipe carrying it narrows because the mass flow rate is constant. The gas flow through a de Laval nozzle is isentropic (gas entropy is nearly constant). At subsonic flow the gas is compressible; sound, a small pressure wave, will propagate through it. At the "throat", where the cross sectional area is a minimum, the gas velocity locally becomes sonic (Mach number = 1.0), a condition called choked flow. As the nozzle cross sectional area increases the gas continues to expand and the gas flow increases to supersonic velocities where a sound wave will not propagate backwards through the gas as viewed in the frame of reference of the nozzle (Mach number > 1.0). De Laval nozzle De Laval nozzle A de Laval nozzle will only choke at the throat if the pressure and mass flow through the nozzle is sufficient to reach sonic speeds, otherwise no supersonic flow is achieved. In addition, the pressure of the gas at the exit of the expansion portion of the exhaust of a nozzle must not be too low. Because pressure cannot travel upstream through the supersonic flow, the exit pressure can be significantly below ambient pressure it exhausts into, but if it is too far below ambient, then the flow will cease to be supersonic, or the flow will separate within the expansion portion of the nozzle, forming an unstable jet that may 'flop' around within the nozzle, possibly damaging it. In practice ambient pressure must be no higher than roughly 2-3 times the pressure in the supersonic gas at the exit for supersonic flow to leave the nozzle. Nozzle efficiency Due to friction between the fluid and walls of the nozzle, the expansion process is irreversible, although still approximately adiabatic. In nozzle design, the usual practice is to base all calculation on isentropic flow and then to make an allowance for friction using a coeficient or efficiency. Nozzle efficiency The nozzle efficiency, ηn, is defined as the ratio of the actual enthalpy drop to the isentropic enthalpy drop Nozzle efficiency If the actual velocity at exit from the nozzle is V1 and the velocity at exit when the flow is isentropic is V1s, then : When the inlet is very small, then Calculation examples 1. Steam is expanded in a set of nozzle from 10 bar. 300 0C to 2 bar. Are the nozzle convergent or convergent- divergent? Neglecting the initial velocity, find the minimum area of the nozzle to flow 1 kg/s of steam, Assume isentropic expansion. Calculation examples No.1No.1 Calculation examples 2. Steam expands in a set of nozzle from 10 bar, 300 0C to 1 bar. The convergent parts of the nozzle are sharp and frictionless. In the divergent parts, the friction loss may be taken as 0.15 of the isentropic enthalpy drop. If the steam floe rate is 1 kg/s and the initial velocity of steam is negligible, find the minimum area of the nozzle. If the exit diameter of nozzle is 25 mm, find the number of nozzles. Calculation examples No.2No.2 Calculation examples 3. Air at 7.8 bar and 180 0C expands through a convergent divergent nozzle into a space at 1.03 bar. The flow rate of air is 3.6 kg/s. Assuming isentropic flow throughout and neglecting the inlet velocity, calculate the throat and exit areas of the nozzle. Calculation examples No.3No.3 Calculation examples 4. Combustion gases expand in a propulsion nozzle from 3.8 bar and 450 0C to a back pressure of 1 bar at the rate of 16 kg/s.
Load more

Recommended publications
  • Rocket Nozzles: 75 Years of Research and Development
    Sådhanå Ó (2021) 46:76 Indian Academy of Sciences https://doi.org/10.1007/s12046-021-01584-6Sadhana(0123456789().,-volV)FT3](0123456789().,-volV) Rocket nozzles: 75 years of research and development SHIVANG KHARE1 and UJJWAL K SAHA2,* 1 Department of Energy and Process Engineering, Norwegian University of Science and Technology, 7491 Trondheim, Norway 2 Department of Mechanical Engineering, Indian Institute of Technology Guwahati, Guwahati 781039, India e-mail: [email protected]; [email protected] MS received 28 August 2020; revised 20 December 2020; accepted 28 January 2021 Abstract. The nozzle forms a large segment of the rocket engine structure, and as a whole, the performance of a rocket largely depends upon its aerodynamic design. The principal parameters in this context are the shape of the nozzle contour and the nozzle area expansion ratio. A careful shaping of the nozzle contour can lead to a high gain in its performance. As a consequence of intensive research, the design and the shape of rocket nozzles have undergone a series of development over the last several decades. The notable among them are conical, bell, plug, expansion-deflection and dual bell nozzles, besides the recently developed multi nozzle grid. However, to the best of authors’ knowledge, no article has reviewed the entire group of nozzles in a systematic and comprehensive manner. This paper aims to review and bring all such development in one single frame. The article mainly focuses on the aerodynamic aspects of all the rocket nozzles developed till date and summarizes the major findings covering their design, development, utilization, benefits and limitations.
    [Show full text]
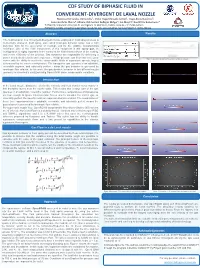
  • Cdf Study of Biphasic Fluid in Convergent-Divergent De
    CDF STUDY OF BIPHASIC FLUID IN CONVERGENT-DIVERGENT DE LAVAL NOZZLE Maricruz Hernández-Hernández1, Victor Hugo Mercado-Lemus1, Hugo Arcos Gutiérrez2, Isaías Garduño-Olvera2, Adriana Del Carmen Gallegos Melgar1, Jan Mayen2, Raul Pérez Bustamante1. 1CONACYT, Corporación Mexicana de Investigación en Materiales, Saltillo, Coahuila, C.P. 25290, México. 2CONACYT, CIATEQ, Unidad San Luis Potosí, Eje 126 No. 225, Zona Industrial, San Luis Potosí C.P. 78395, México. Abstract Results The fluid behavior in a convergent-divergent nozzle employed in Cold spray process is numerically analyzed. Cold spray, also called Cold gas dynamic spray, has a high potential, both for the generation of coatings and for the additive manufacturing technique. One of the main components of this equipment is the spray gun, its configuration is highly important in the control of the final characteristics of the coating, and in the efficiency of the process. Gas dynamics are responsible for delivering a power at a desired velocity and temperature. A high-pressure gas flows into a de Laval Figure 1:Geometry domain and boundary conditions of nozzle. nozzle with the ability to accelerate compressible fluids at supersonic speeds, largely determined by the nozzle configuration. The transporter gas operates in an adiabatic, reversible regimen, and calorically perfect - mean the gas behavior is governed by isentropic flow relation. In this work, the gas dynamic behavior in two different nozzle geometry is numerically analyzed using OpenFOAM under compressible conditions. Introduction In the Laval nozzle, dissipative effects like viscosity and heat transfer occur mainly in thin boundary layers near the nozzle walls. This means that a large part of the gas operates in an adiabatic, reversible regimen.
    [Show full text]
  • Supersonic Air and Wet Steam Jet Using Simplified De Laval Nozzle
    Proceedings of the International Conference on Power Engineering-15 (ICOPE-15) November 30- December 4, 2015, Yokohama, Japan Paper ID: ICOPE-15-1158 Supersonic air and wet steam jet using simplified de Laval nozzle Takumi Komori*, Masahiro Miura*, Sachiyo Horiki* and Masahiro OSAKABE* * Tokyo University of Marine Science & Technology 2-1-6Etchujima, Koto-ku, Tokyo 135-8533, Japan E-mail: [email protected] Abstract Usually, Trichloroethane has been used for the de-oiling and cleaning of machine parts. But its production and import have been prohibited since 1995 because of its possibility to destroy the ozone layer. Generally for biological and environmental safety, the de-oiling should be done with the physical method instead of the chemical method using detergent or solvent. As one of the physical method, a cleaning by a supersonic wet steam jet has been proposed. The steam jet with water droplets impinges on the oily surface of machine parts and removes the oil or smudge. In the present study, the low-cost and taper-shaped nozzles were fabricated with an electric discharge machining. The jet behaviors from the taper-shaped nozzles were carefully observed by using air and wet steam. The non-equilibrium model of wet steam was proposed and compared with the experimental results. The spatial distribution of low density regions along the jet axis was considered to contribute the cleaning and de-oiling. However, the condensate generated with the depressurization of steam depressed the injected steam mass flow rate. Furthermore, the steam cleaning was conducted for the plastic coin and the good cleaning effect could be confirmed in spite of the short cleaning duration.
    [Show full text]
  • Flow Analysis of Rocket Nozzle Using Method of Characteristics
    FLOW ANALYSIS OF ROCKET NOZZLE USING METHOD OF CHARACTERISTICS Dipen R. Dangi1, Parth B. Thaker2, Atal B. Harichandan3 1, 2, 3 Department of Mechanical Engineering, Marwadi Education Foundation, (India) ABSTRACT The present research work has been carried out for the analysis of bell type nozzle by using method of characteristic with different Mach number conditions. A C-code has been developed to define the nozzle geometry by using method of characteristics usually designed for De-Laval nozzle. ANSYS 14.0 has been used for the present flow analysis by considering hear Stress Transport k-ω (SSTKW) turbulence model. In this paper CFD is used to develop best geometry of rocket nozzle with consider of aero - thermodynamic property like pressure, velocity, temperature and Mach number. Keywords: Design Of Supersonic Nozzle, Method Of Characteristic And Minimum Length Of Nozzle. I INTRODUCTION Performance of rocket nozzle is always less than the theoretical approach in all practical approaches. It is always essential to improve the performance of rocket nozzle. Previous research works show the De- Laval nozzle is the most efficient nozzle among all other types of nozzles. The De-Laval nozzle gives the best performance rocket nozzle as Mach number and velocity of fluid flow is continuously increasing while at same time pressure is continuously decreasing. But still some research gap is there to develop best geometry of rocket nozzle. Even today most of the engineers are work on how to develop best geometry of rocket nozzle and to achieve higher Mach number and higher velocity of fluid flow. Due to that reason authors works on the Method of Characteristics (MOC) and developed best geometry which gives possible optimum values of Mach number, velocity, pressure distribution and density distribution.
    [Show full text]
  • Rocket Nozzles the Simplest Nozzle Is a Cone with a Half-Opening Angle, Α Attached to a Combustion Chamber (See Figure 3)
    NOZZLES S. R. KULKARNI 1. Motivation In astronomy textbooks it is usually stated that the Bondi-Hoyle solution has a specific value for the accretion rate (given the boundary conditions of ambient density and temper- ature of the gas). Only with this specific accretion rate will there be a seamless transition from sub-sonic inflow to super-sonic inflow. The Bondi-Hoyle or the Parker problem is quite analogous to the rocket problem, in that both involve a smooth transition from sub-sonic to super-sonic flow. What bothered me is the statement in astronomy books that the solution demands a specific accretion (or excretion) mass rate. In contrast, the thrust on a rocket can be varied (as can be gathered if you watch NASA TV). Given the similarity between the astronomical problem and the rocket problem I thought an investigation of the latter may be illuminating and hence this note. 2. The de Laval Nozzle Consider a rocket which is burning fuel. Let M˙ be the burn rate of the fuel and ue be the speed of the exhaust. Then in steady state the vertical “thrust” or force is Mu˙ e. The resulting vertical thrust lifts the rocket. Clearly, it is of greatest advantage to make the exhaust speed as large as possible and to minimize the outflow in directions other than vertical. A rocket engine consists of a chamber in which fuel is burnt connected to a nozzle. A properly designed1 nozzle can convert the hot burnt fuel into supersonic flow (see Figure 1). The integration of the momentum equation (under assumptions of inviscid flow) yields the much celebrated Beronulli’s theorem.
    [Show full text]
  • Characterization of Non-Equilibrium Condensation of Supercritical Carbon Dioxide in a De Laval Nozzle
    Characterization of Non-Equilibrium Condensation of Supercritical Carbon Dioxide in a de Laval Nozzle The MIT Faculty has made this article openly available. Please share how this access benefits you. Your story matters. Citation Lettieri, Claudio, Derek Paxson, Zoltan Spakovszky, and Peter Bryanston-Cross. “Characterization of Non-Equilibrium Condensation of Supercritical Carbon Dioxide in a de Laval Nozzle.” Volume 9: Oil and Gas Applications; Supercritical CO2 Power Cycles; Wind Energy (June 26, 2017). As Published http://dx.doi.org/10.1115/GT2017-64641 Publisher ASME International Version Final published version Citable link http://hdl.handle.net/1721.1/116087 Terms of Use Article is made available in accordance with the publisher's policy and may be subject to US copyright law. Please refer to the publisher's site for terms of use. Proceedings of ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition GT2017 June 26-30, 2017, Charlotte, NC, USA GT2017-64641 CHARACTERIZATION OF NON-EQUILIBRIUM CONDENSATION OF SUPERCRITICAL CARBON DIOXIDE IN A DE LAVAL NOZZLE Claudio Lettieri Derek Paxson Delft University of Technology Massachusetts Institute of Technology Delft, The Netherlands Cambridge, MA, USA Zoltan Spakovszky Peter Bryanston-Cross Massachusetts Institute of Technology Warwick University Cambridge, MA, USA Coventry, UK ABSTRACT data, with improved accuracy at conditions away from the On a ten-year timescale, Carbon Capture and Storage could critical point. The results are applied in a pre-production significantly reduce carbon dioxide (CO2) emissions. One of supercritical carbon dioxide compressor and are used to define the major limitations of this technology is the energy penalty inlet conditions at reduced temperature but free of for the compression of CO2 to supercritical conditions, which condensation.
    [Show full text]
  • Performance Evaluation of an IC Engine in the Presence of a C-D Nozzle in the Air Intake Manifold
    International Journal of Current Engineering and Technology ISSN 2277 - 4106 © 2013 INPRESSCO. All Rights Reserved. Available at http://inpressco.com/category/ijcet Research Article Performance Evaluation of an IC Engine in the Presence of a C-D Nozzle in the Air Intake Manifold S.Ravi Babu*a, K.Prasada Raoa and P.Ramesh Babua aDepartment of Mechanical Engineering, GMR Institute of Technology, Rajam, India Accepted 10 August 2013, Available online 01 October 2013, Vol.3, No.4 (October 2013) Abstract The present day energy crisis and ever increasing demands of energy in addition to global pollution brought us into a situation where there is an urgent need for energy conservation, efficient utilization and eco-friendly techniques to be implemented in day to day use. These needs lead us to an idea of modified design in a CI engine without any additional energy requirement and with no complicated variations in design. There are various other methods to improve the efficiency of engine such as super charging, turbo charging, varying stroke length, varying injection pressure, fuel to air ratio, additional strokes per cycle and so on. Many of them require additional design (stroke length, injection pressure etc.,) and some of them load to increase environmental effect. Here in this project affords were made to increase the velocity (physical parameter) of air entering the inlet manifold of the engine by inserting a convergent divergent nozzle at the inlet manifold. There by increasing the mixture quality of air & fuel in the combustion chamber before the initialization of ignition. The engine load tests were carried out at different loads, variation of different parameters with load was plotted.
    [Show full text]
  • Design of a Small-Scaled De Laval Nozzle for IGLIS Experiment
    Design of a small-scaled de Laval nozzle for IGLIS experiment Evgeny Mogilevskiy, R. Ferrer, L. Gaffney, C. Granados, M. Huyse, Yu. Kudryavtsev, S. Raeder, P. Van Duppen Instituut voor Kern- en Stralingsfysika, KU Leuven, Celestijnenlaan 200 D, B-3001 Leuven, Belgium. Outline • IGLIS technique and requirements for a gas jet • Classical way of a nozzle design – Method of characteristics – Boundary layer correction • Iterative method based on CFD with COMSOL • Conclusions and further steps IGLIS= In Gas Laser Ionization Spectroscopy Differential Gas cell chamber Extraction pumping chamber chamber S-shaped RFQ de Laval nozzle Gas Cell Ion collector Towards mass Gas jet separator gas Extraction RFQ Extraction electrode from in-flight separator One-dimension laser beam expander Thing Position of the λ1 λ2 λ2 λ1 entrance stopped nuclei In-gas-jet window In-gas-cell ionization ionization 1·10-5-2·10 -3 -2 < 1e-5 mbar 1·10 -2 mbar mbar •Products of a nuclear reaction get into the gas cell (Argon or Helium, 500 mbar) •Atoms are neutralized and stopped in the cell, then transported towards the nozzle •Two-step ionization is used for resonance ionization of the specified element Requirements for the jet • Cold enough with no pressure (high Mach number) – No Doppler and pressure broadening • Long enough with no shocks (uniform) – Enough space and time to light up all the atoms • Small enough flow rate – Pumping system capacity Small scaled de Laval nozzle is required De Laval Nozzle Convergent-divergent nozzle: A – area of a cross-section, V – gas velocity, M – Mach number Pressure, temperature and density along the nozzle Quantitative characteristics Parameter Aeronautics [1] Chemical study [2] IGLIS[3] Stagnation pressure 10^3 atm 10^(-5) atm 10^(-1) atm Stagnation 2000K 300K 300 K temperature Throat size 3 mm 25 mm 1 mm Exit Mach number 6 to 15 4 8 to 12 Gas Air Helium Argon Reynolds number 10^6 4000 3000 (in throat) [1] J.J.
    [Show full text]
  • Space Advantage Provided by De-Laval Nozzle and Bell Nozzle Over Venturi
    Proceedings of the World Congress on Engineering 2015 Vol II WCE 2015, July 1 - 3, 2015, London, U.K. Space Advantage Provided by De-Laval Nozzle and Bell Nozzle over Venturi Omkar N. Deshpande, Nitin L. Narappanawar Abstract:-The FSAE guidelines state that it is mandatory for many crucial components are to be fitted in a very little each and every car participating in the said event to have a space. Therefore there is a need to design a new kind of single circular 20mm restrictor in the intake system. All the air nozzle achieving optimality at a higher angle than that of the flowing to the engine must pass through this restrictor. Conventionally, a Venturi Nozzle is used as a restrictor. In our venturi nozzle. For this purpose De Laval Nozzle and Bell research, we have proposed two Nozzles: De-Laval Nozzle and Nozzle are analyzed as a possible alternative to the venturi. Bell Nozzle as an alternative to the Venturi Nozzle. After De- Laval Nozzle is used in certain type of steam turbines numerous CFD Simulations; we have inferred that the results and also as a Rocket Engine Nozzle [6]. Bell Nozzle is also of the De-Laval Nozzle and Bell Nozzle are similar to the widely used as a Rocket Engine Nozzle. Both of the nozzles Venturi Nozzle. Along with providing similar results, the two achieve optimality at a higher angle of convergence as nozzles provide a space saving of 6.86% over the Venturi Nozzle. The data was gathered from SolidWorks Flow demonstrated in ‘Section V parts A.); B.).’ Simulation 2014.
    [Show full text]
  • Section1: " Compressible Flow: Historical Perspective and Basic Definitions!
    Section1: " Compressible Flow: Historical Perspective and Basic Definitions! Anderson: Chapter 1 pp. 1-19! 1! MAE 5420 - Compressible Fluid Flow! De Laval Nozzle! • High Speed flows often seem “counter-intuitive” when! Compared with low speed flows! • Example: Convergent-Divergent Nozzle (De Laval)! !In 1897 Swedish Engineer Gustav De Laval designed! !!A turbine wheel powered by 4- steam nozzles! !!De Laval Discovered that if the steam nozzle ! Credit: NASA!! GSFC! first narrowed, and then expanded, the efficiency of! !!the turbine was increased dramatically ! flow !!Furthermore, the ratio of the minimum area! !!to the inlet and outlet areas was critical for achieving! !!maximum efficiency … Counter to the “wisdom” of the day! Convergent / Divergent Nozzle 2! MAE 5420 - Compressible Fluid Flow! De Laval Nozzle (cont’d)! • Mechanical Engineers of the 19’th century were! Primarily “hydrodynamicists” .. That is they were! Familiar with fluids that were incompressible … liquids! and Low speed gas flows where fluid density was! Essentially constant! • Primary Principles are Continuity and Bernoulli’s Law! 3! MAE 5420 - Compressible Fluid Flow! De Laval Nozzle (cont’d)! • When Continuity and Bernoulli are applied to a ! De Laval Nozzle and density is Assumed constant! High Pressure Inlet! pI! pe! pt! VI! A A Ve! I At Vt! e AI! A ! Ae! ! t ! At Throat! ! • Pressure Drop! • Velocity Increases! Continuity! Bernoulli! “classic” Venturi! 4! MAE 5420 - Compressible Fluid Flow! De Laval Nozzle (cont’d)! • When Continuity and Bernoulli are applied to a ! De
    [Show full text]
  • Concepts and Cfd Analysis of De-Laval Nozzle
    International Journal of Mechanical Engineering and Technology (IJMET) Volume 7, Issue 5, September–October 2016, pp.221–240, Article ID: IJMET_07_05_024 Available online at http://iaeme.com/Home/issue/IJMET?Volume=7&Issue=5 Journal Impact Factor (2016): 9.2286 (Calculated by GISI) www.jifactor.com ISSN Print: 0976-6340 and ISSN Online: 0976-6359 © IAEME Publication CONCEPTS AND CFD ANALYSIS OF DE-LAVAL NOZZLE Malay S Patel, Sulochan D Mane and Manikant Raman Mechanical Engineering Department, Dr. D.Y Patil Institute of Engineering and Technology, Pune, India. ABSTRACT Anozzle is a device designed to control the characteristics of fluid. It is mostly used to increase the velocity of fluid. A typical De-Laval nozzle is a nozzle which has a converging part, throat and diverging part. This paper aims at explaining most of the concepts related to De Laval nozzle. In this paper the principle of working of nozzle is discussed. Theoretical analysis of flow is also done at different points of nozzle. The variation of flow parameters like Pressure, Temperature, Velocity and Density is visualized using Computational Fluid Dynamics. The simulation of shockwave through CFD is also done. Key words: Rocket engine nozzle, De-Laval nozzle, Ideal gas, Computational Fluid dynamics, Ansys-Fluent. Cite this Article: Malay S Patel, Sulochan D Mane and Manikant Raman, Concepts and CFD Analysis of De-Laval Nozzle. International Journal of Mechanical Engineering and Technology, 7(5), 2016, pp. 221–240. http://iaeme.com/Home/issue/IJMET?Volume=7&Issue=5 1. INTRODUCTION
    [Show full text]
  • Preliminary Design Document ASEN 4018
    Preliminary Design Document ASEN 4018 1 of 28 American Institute of Aeronautics and Astronautics Preliminary Design Document ASEN 4018 Contents 2 Project Description 3 2.1 Project Purpose . 3 2.2 Objectives . 3 2.3 CONOPS . 4 2.4 Functional Block Diagram . 5 2.5 Functional Requirements . 6 3 Design Requirements 7 4 Key Design Options Considered 9 4.1 Nozzle Design . 9 4.1.1 de Laval Nozzle . 10 4.1.2 Annular Convergent-Divergent Nozzle (ACD Nozzle) . 10 4.1.3 Variable Geometry Nozzle . 11 4.1.4 Expansion-Deflection Nozzle . 12 4.1.5 Minimum Length Nozzle (MLN) . 13 4.1.6 Heat Transfer for Flow Velocity Control . 13 4.2 Nozzle Testbed . 14 4.2.1 Testing on JetCat Engine vs. Engine Analogue . 14 4.2.2 Hot-flow vs. Cold-flow Testbed . 15 4.2.3 Actual Size vs. Scaled Nozzle . 17 4.3 Nozzle Integration . 18 4.3.1 Complete Nozzle Replacement . 18 4.3.2 Nozzle extension and Overlapping Extension . 19 4.3.3 Nozzle Dome Replacement . 21 5 Trade Study Process and Results 23 5.1 Nozzle Design . 23 5.1.1 Trade Elements . 23 5.1.2 Trade Study . 23 5.2 Nozzle Testbed . 24 5.2.1 Trade Elements . 24 5.2.2 Trade Study . 25 5.3 Nozzle Integration . 25 5.3.1 Trade Elements . 25 5.3.2 Trade Study . 26 6 Selection of Baseline Design 26 6.1 Nozzle Aerodynamics . 26 6.2 Nozzle Test Bed . 27 6.3 Nozzle Integration . 27 2 of 28 American Institute of Aeronautics and Astronautics Preliminary Design Document ASEN 4018 2.
    [Show full text]