Space-Efficient Data Structures for Top-K Completion
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Application of TRIE Data Structure and Corresponding Associative Algorithms for Process Optimization in GRID Environment
Application of TRIE data structure and corresponding associative algorithms for process optimization in GRID environment V. V. Kashanskya, I. L. Kaftannikovb South Ural State University (National Research University), 76, Lenin prospekt, Chelyabinsk, 454080, Russia E-mail: a [email protected], b [email protected] Growing interest around different BOINC powered projects made volunteer GRID model widely used last years, arranging lots of computational resources in different environments. There are many revealed problems of Big Data and horizontally scalable multiuser systems. This paper provides an analysis of TRIE data structure and possibilities of its application in contemporary volunteer GRID networks, including routing (L3 OSI) and spe- cialized key-value storage engine (L7 OSI). The main goal is to show how TRIE mechanisms can influence de- livery process of the corresponding GRID environment resources and services at different layers of networking abstraction. The relevance of the optimization topic is ensured by the fact that with increasing data flow intensi- ty, the latency of the various linear algorithm based subsystems as well increases. This leads to the general ef- fects, such as unacceptably high transmission time and processing instability. Logically paper can be divided into three parts with summary. The first part provides definition of TRIE and asymptotic estimates of corresponding algorithms (searching, deletion, insertion). The second part is devoted to the problem of routing time reduction by applying TRIE data structure. In particular, we analyze Cisco IOS switching services based on Bitwise TRIE and 256 way TRIE data structures. The third part contains general BOINC architecture review and recommenda- tions for highly-loaded projects. -

An Alternative to Fibonacci Heaps with Worst Case Rather Than Amortized Time Bounds∗
Relaxed Fibonacci heaps: An alternative to Fibonacci heaps with worst case rather than amortized time bounds¤ Chandrasekhar Boyapati C. Pandu Rangan Department of Computer Science and Engineering Indian Institute of Technology, Madras 600036, India Email: [email protected] November 1995 Abstract We present a new data structure called relaxed Fibonacci heaps for implementing priority queues on a RAM. Relaxed Fibonacci heaps support the operations find minimum, insert, decrease key and meld, each in O(1) worst case time and delete and delete min in O(log n) worst case time. Introduction The implementation of priority queues is a classical problem in data structures. Priority queues find applications in a variety of network problems like single source shortest paths, all pairs shortest paths, minimum spanning tree, weighted bipartite matching etc. [1] [2] [3] [4] [5] In the amortized sense, the best performance is achieved by the well known Fibonacci heaps. They support delete and delete min in amortized O(log n) time and find min, insert, decrease key and meld in amortized constant time. Fast meldable priority queues described in [1] achieve all the above time bounds in worst case rather than amortized time, except for the decrease key operation which takes O(log n) worst case time. On the other hand, relaxed heaps described in [2] achieve in the worst case all the time bounds of the Fi- bonacci heaps except for the meld operation, which takes O(log n) worst case ¤Please see Errata at the end of the paper. 1 time. The problem that was posed in [1] was to consider if it is possible to support both decrease key and meld simultaneously in constant worst case time. -

KP-Trie Algorithm for Update and Search Operations
The International Arab Journal of Information Technology, Vol. 13, No. 6, November 2016 KP-Trie Algorithm for Update and Search Operations Feras Hanandeh1, Mohammed Akour2, Essam Al Daoud3, Rafat Alshorman4, Izzat Alsmadi5 1Dept. of Computer Information Systems, Faculty of Prince Al-Hussein Bin Abdallah II For Information Technology, Hashemite University, Zarqa, Jordan, [email protected] 2,5Dept. of Computer Information Systems, Faculty of Information Technology, Yarmouk University, Irbid, Jordan, [email protected], [email protected] 3,4Computer Science Department, Zarqa University [email protected]; [email protected] Abstract: Radix-Tree is a space optimized data structure that performs data compression by means of cluster nodes that share the same branch. Each node with only one child is merged with its child and is considered as space optimized. Nevertheless, it can't be considered as speed optimized because the root is associated with the empty string . Moreover, values are not normally associated with every node; they are associated only with leaves and some inner nodes that correspond to keys of interest. Therefore, it takes time in moving bit by bit to reach the desired word. In this paper we propose the KP-Trie which is consider as speed and space optimized data structure that is resulted from both horizontal and vertical compression. Keywords: Trie, radix tree, data structure, branch factor, indexing, tree structure, information retrieval. 1- Introduction The concept of Data structures such as trees has developed since the 19th century. Tries evolved from trees. They have different names Data structures are a specialized format for such as: Radix tree, prefix tree compact trie, efficient organizing, retrieving, saving and bucket trie, crit bit tree, and PATRICIA storing data. -

C Programming: Data Structures and Algorithms
C Programming: Data Structures and Algorithms An introduction to elementary programming concepts in C Jack Straub, Instructor Version 2.07 DRAFT C Programming: Data Structures and Algorithms, Version 2.07 DRAFT C Programming: Data Structures and Algorithms Version 2.07 DRAFT Copyright © 1996 through 2006 by Jack Straub ii 08/12/08 C Programming: Data Structures and Algorithms, Version 2.07 DRAFT Table of Contents COURSE OVERVIEW ........................................................................................ IX 1. BASICS.................................................................................................... 13 1.1 Objectives ...................................................................................................................................... 13 1.2 Typedef .......................................................................................................................................... 13 1.2.1 Typedef and Portability ............................................................................................................. 13 1.2.2 Typedef and Structures .............................................................................................................. 14 1.2.3 Typedef and Functions .............................................................................................................. 14 1.3 Pointers and Arrays ..................................................................................................................... 16 1.4 Dynamic Memory Allocation ..................................................................................................... -

Balanced Trees Part One
Balanced Trees Part One Balanced Trees ● Balanced search trees are among the most useful and versatile data structures. ● Many programming languages ship with a balanced tree library. ● C++: std::map / std::set ● Java: TreeMap / TreeSet ● Many advanced data structures are layered on top of balanced trees. ● We’ll see several later in the quarter! Where We're Going ● B-Trees (Today) ● A simple type of balanced tree developed for block storage. ● Red/Black Trees (Today/Thursday) ● The canonical balanced binary search tree. ● Augmented Search Trees (Thursday) ● Adding extra information to balanced trees to supercharge the data structure. Outline for Today ● BST Review ● Refresher on basic BST concepts and runtimes. ● Overview of Red/Black Trees ● What we're building toward. ● B-Trees and 2-3-4 Trees ● Simple balanced trees, in depth. ● Intuiting Red/Black Trees ● A much better feel for red/black trees. A Quick BST Review Binary Search Trees ● A binary search tree is a binary tree with 9 the following properties: 5 13 ● Each node in the BST stores a key, and 1 6 10 14 optionally, some auxiliary information. 3 7 11 15 ● The key of every node in a BST is strictly greater than all keys 2 4 8 12 to its left and strictly smaller than all keys to its right. Binary Search Trees ● The height of a binary search tree is the 9 length of the longest path from the root to a 5 13 leaf, measured in the number of edges. 1 6 10 14 ● A tree with one node has height 0. -

Data Structures and Algorithms Binary Heaps (S&W 2.4)
Data structures and algorithms DAT038/TDA417, LP2 2019 Lecture 12, 2019-12-02 Binary heaps (S&W 2.4) Some slides by Sedgewick & Wayne Collections A collection is a data type that stores groups of items. stack Push, Pop linked list, resizing array queue Enqueue, Dequeue linked list, resizing array symbol table Put, Get, Delete BST, hash table, trie, TST set Add, ontains, Delete BST, hash table, trie, TST A priority queue is another kind of collection. “ Show me your code and conceal your data structures, and I shall continue to be mystified. Show me your data structures, and I won't usually need your code; it'll be obvious.” — Fred Brooks 2 Priority queues Collections. Can add and remove items. Stack. Add item; remove the item most recently added. Queue. Add item; remove the item least recently added. Min priority queue. Add item; remove the smallest item. Max priority queue. Add item; remove the largest item. return contents contents operation argument value size (unordered) (ordered) insert P 1 P P insert Q 2 P Q P Q insert E 3 P Q E E P Q remove max Q 2 P E E P insert X 3 P E X E P X insert A 4 P E X A A E P X insert M 5 P E X A M A E M P X remove max X 4 P E M A A E M P insert P 5 P E M A P A E M P P insert L 6 P E M A P L A E L M P P insert E 7 P E M A P L E A E E L M P P remove max P 6 E M A P L E A E E L M P A sequence of operations on a priority queue 3 Priority queue API Requirement. -

Abstract Data Types
Chapter 2 Abstract Data Types The second idea at the core of computer science, along with algorithms, is data. In a modern computer, data consists fundamentally of binary bits, but meaningful data is organized into primitive data types such as integer, real, and boolean and into more complex data structures such as arrays and binary trees. These data types and data structures always come along with associated operations that can be done on the data. For example, the 32-bit int data type is defined both by the fact that a value of type int consists of 32 binary bits but also by the fact that two int values can be added, subtracted, multiplied, compared, and so on. An array is defined both by the fact that it is a sequence of data items of the same basic type, but also by the fact that it is possible to directly access each of the positions in the list based on its numerical index. So the idea of a data type includes a specification of the possible values of that type together with the operations that can be performed on those values. An algorithm is an abstract idea, and a program is an implementation of an algorithm. Similarly, it is useful to be able to work with the abstract idea behind a data type or data structure, without getting bogged down in the implementation details. The abstraction in this case is called an \abstract data type." An abstract data type specifies the values of the type, but not how those values are represented as collections of bits, and it specifies operations on those values in terms of their inputs, outputs, and effects rather than as particular algorithms or program code. -

Game Trees, Quad Trees and Heaps
CS 61B Game Trees, Quad Trees and Heaps Fall 2014 1 Heaps of fun R (a) Assume that we have a binary min-heap (smallest value on top) data structue called Heap that stores integers and has properly implemented insert and removeMin methods. Draw the heap and its corresponding array representation after each of the operations below: Heap h = new Heap(5); //Creates a min-heap with 5 as the root 5 5 h.insert(7); 5,7 5 / 7 h.insert(3); 3,7,5 3 /\ 7 5 h.insert(1); 1,3,5,7 1 /\ 3 5 / 7 h.insert(2); 1,2,5,7,3 1 /\ 2 5 /\ 7 3 h.removeMin(); 2,3,5,7 2 /\ 3 5 / 7 CS 61B, Fall 2014, Game Trees, Quad Trees and Heaps 1 h.removeMin(); 3,7,5 3 /\ 7 5 (b) Consider an array based min-heap with N elements. What is the worst case running time of each of the following operations if we ignore resizing? What is the worst case running time if we take into account resizing? What are the advantages of using an array based heap vs. using a BST-based heap? Insert O(log N) Find Min O(1) Remove Min O(log N) Accounting for resizing: Insert O(N) Find Min O(1) Remove Min O(N) Using a BST is not space-efficient. (c) Your friend Alyssa P. Hacker challenges you to quickly implement a max-heap data structure - "Hah! I’ll just use my min-heap implementation as a template", you think to yourself. -
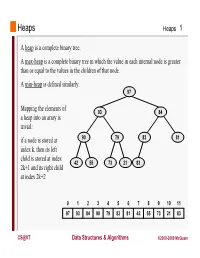
Heaps a Heap Is a Complete Binary Tree. a Max-Heap Is A
Heaps Heaps 1 A heap is a complete binary tree. A max-heap is a complete binary tree in which the value in each internal node is greater than or equal to the values in the children of that node. A min-heap is defined similarly. 97 Mapping the elements of 93 84 a heap into an array is trivial: if a node is stored at 90 79 83 81 index k, then its left child is stored at index 42 55 73 21 83 2k+1 and its right child at index 2k+2 01234567891011 97 93 84 90 79 83 81 42 55 73 21 83 CS@VT Data Structures & Algorithms ©2000-2009 McQuain Building a Heap Heaps 2 The fact that a heap is a complete binary tree allows it to be efficiently represented using a simple array. Given an array of N values, a heap containing those values can be built, in situ, by simply “sifting” each internal node down to its proper location: - start with the last 73 73 internal node * - swap the current 74 81 74 * 93 internal node with its larger child, if 79 90 93 79 90 81 necessary - then follow the swapped node down 73 * 93 - continue until all * internal nodes are 90 93 90 73 done 79 74 81 79 74 81 CS@VT Data Structures & Algorithms ©2000-2009 McQuain Heap Class Interface Heaps 3 We will consider a somewhat minimal maxheap class: public class BinaryHeap<T extends Comparable<? super T>> { private static final int DEFCAP = 10; // default array size private int size; // # elems in array private T [] elems; // array of elems public BinaryHeap() { . -

Priority Queues and Binary Heaps Chapter 6.5
Priority Queues and Binary Heaps Chapter 6.5 1 Some animals are more equal than others • A queue is a FIFO data structure • the first element in is the first element out • which of course means the last one in is the last one out • But sometimes we want to sort of have a queue but we want to order items according to some characteristic the item has. 107 - Trees 2 Priorities • We call the ordering characteristic the priority. • When we pull something from this “queue” we always get the element with the best priority (sometimes best means lowest). • It is really common in Operating Systems to use priority to schedule when something happens. e.g. • the most important process should run before a process which isn’t so important • data off disk should be retrieved for more important processes first 107 - Trees 3 Priority Queue • A priority queue always produces the element with the best priority when queried. • You can do this in many ways • keep the list sorted • or search the list for the minimum value (if like the textbook - and Unix actually - you take the smallest value to be the best) • You should be able to estimate the Big O values for implementations like this. e.g. O(n) for choosing the minimum value of an unsorted list. • There is a clever data structure which allows all operations on a priority queue to be done in O(log n). 107 - Trees 4 Binary Heap Actually binary min heap • Shape property - a complete binary tree - all levels except the last full. -

Assignment 3: Kdtree ______Due June 4, 11:59 PM
CS106L Handout #04 Spring 2014 May 15, 2014 Assignment 3: KDTree _________________________________________________________________________________________________________ Due June 4, 11:59 PM Over the past seven weeks, we've explored a wide array of STL container classes. You've seen the linear vector and deque, along with the associative map and set. One property common to all these containers is that they are exact. An element is either in a set or it isn't. A value either ap- pears at a particular position in a vector or it does not. For most applications, this is exactly what we want. However, in some cases we may be interested not in the question “is X in this container,” but rather “what value in the container is X most similar to?” Queries of this sort often arise in data mining, machine learning, and computational geometry. In this assignment, you will implement a special data structure called a kd-tree (short for “k-dimensional tree”) that efficiently supports this operation. At a high level, a kd-tree is a generalization of a binary search tree that stores points in k-dimen- sional space. That is, you could use a kd-tree to store a collection of points in the Cartesian plane, in three-dimensional space, etc. You could also use a kd-tree to store biometric data, for example, by representing the data as an ordered tuple, perhaps (height, weight, blood pressure, cholesterol). However, a kd-tree cannot be used to store collections of other data types, such as strings. Also note that while it's possible to build a kd-tree to hold data of any dimension, all of the data stored in a kd-tree must have the same dimension. -

L11: Quadtrees CSE373, Winter 2020
L11: Quadtrees CSE373, Winter 2020 Quadtrees CSE 373 Winter 2020 Instructor: Hannah C. Tang Teaching Assistants: Aaron Johnston Ethan Knutson Nathan Lipiarski Amanda Park Farrell Fileas Sam Long Anish Velagapudi Howard Xiao Yifan Bai Brian Chan Jade Watkins Yuma Tou Elena Spasova Lea Quan L11: Quadtrees CSE373, Winter 2020 Announcements ❖ Homework 4: Heap is released and due Wednesday ▪ Hint: you will need an additional data structure to improve the runtime for changePriority(). It does not affect the correctness of your PQ at all. Please use a built-in Java collection instead of implementing your own. ▪ Hint: If you implemented a unittest that tested the exact thing the autograder described, you could run the autograder’s test in the debugger (and also not have to use your tokens). ❖ Please look at posted QuickCheck; we had a few corrections! 2 L11: Quadtrees CSE373, Winter 2020 Lecture Outline ❖ Heaps, cont.: Floyd’s buildHeap ❖ Review: Set/Map data structures and logarithmic runtimes ❖ Multi-dimensional Data ❖ Uniform and Recursive Partitioning ❖ Quadtrees 3 L11: Quadtrees CSE373, Winter 2020 Other Priority Queue Operations ❖ The two “primary” PQ operations are: ▪ removeMax() ▪ add() ❖ However, because PQs are used in so many algorithms there are three common-but-nonstandard operations: ▪ merge(): merge two PQs into a single PQ ▪ buildHeap(): reorder the elements of an array so that its contents can be interpreted as a valid binary heap ▪ changePriority(): change the priority of an item already in the heap 4 L11: Quadtrees CSE373,