DOCSLIB.ORG

Matrix Differential Calculus with Applications in Statistics and Econometrics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Matrix Differential Calculus with Applications in Statistics and Econometrics Matrix Differential Calculus with Applications in Statistics and Econometrics WILEY SERIES IN PROBABILITY AND STATISTICS Established by Walter E. Shewhart and Samuel S. Wilks Editors: David J. Balding, Noel A. C. Cressie, Garrett M. Fitzmaurice, Geof H. Givens, Harvey Goldstein, Geert Molenberghs, David W. Scott, Adrian F. M. Smith, and Ruey S. Tsay Editors Emeriti: J. Stuart Hunter, Iain M. Johnstone, Joseph B. Kadane, and Jozef L. Teugels The Wiley Series in Probability and Statistics is well established and author- itative. It covers many topics of current research interest in both pure and applied statistics and probability theory. Written by leading statisticians and institutions, the titles span both state-of-the-art developments in the field and classical methods. Reflecting the wide range of current research in statistics, the series encom- passes applied, methodological, and theoretical statistics, ranging from ap- plications and new techniques made possible by advances in computerized practice to rigorous treatment of theoretical approaches. This series provides essential and invaluable reading for all statisticians, whether in academia, in- dustry, government, or research. A complete list of the titles in this series can be found at http://www.wiley.com/go/wsps Matrix Differential Calculus with Applications in Statistics and Econometrics Third Edition Jan R. Magnus Department of Econometrics and Operations Research, Vrije Universiteit Amsterdam, The Netherlands and Heinz Neudecker† Amsterdam School of Economics, University of Amsterdam, The Netherlands This third edition first published 2019 c 2019 John Wiley & Sons Edition History John Wiley & Sons (1e, 1988) and John Wiley & Sons (2e, 1999) All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, except as permitted by law. Advice on how to obtain permission to reuse material from this title is available at http://www.wiley.com/go/permissions. The right of Jan R. Magnus and Heinz Neudecker to be identified as the authors of this work has been asserted in accordance with law. Registered Offices John Wiley & Sons, Inc., 111 River Street, Hoboken, NJ 07030, USA John Wiley & Sons Ltd, The Atrium, Southern Gate, Chichester, West Sussex, PO19 8SQ, UK Editorial Office 9600 Garsington Road, Oxford, OX4 2DQ, UK For details of our global editorial offices, customer services, and more information about Wiley products visit us at www.wiley.com. Wiley also publishes its books in a variety of electronic formats and by print-on-demand. Some content that appears in standard print versions of this book may not be available in other formats. Limit of Liability/Disclaimer of Warranty While the publisher and authors have used their best efforts in preparing this work, they make no representations or warranties with respect to the accuracy or completeness of the contents of this work and specifically disclaim all warranties, including without limitation any implied warranties of merchantability or fitness for a particular purpose. No warranty may be created or extended by sales representatives, written sales materials or promotional statements for this work. The fact that an organization, website, or product is referred to in this work as a citation and/or potential source of further information does not mean that the publisher and authors endorse the information or services the organization, website, or product may provide or recommendations it may make. This work is sold with the understanding that the publisher is not engaged in rendering professional services. The advice and strategies contained herein may not be suitable for your situation. You should consult with a specialist where appropriate. Further, readers should be aware that websites listed in this work may have changed or disappeared between when this work was written and when it is read. Neither the publisher nor authors shall be liable for any loss of profit or any other commercial damages, including but not limited to special, incidental, consequential, or other damages. Library of Congress Cataloging-in-Publication Data applied for ISBN: 9781119541202 Cover design by Wiley Cover image: c phochi/Shutterstock Typeset by the author in LATEX 10987654321 Contents Preface ....................................xiii Part One — Matrices 1 Basic properties of vectors and matrices 3 1 Introduction............................. 3 2 Sets ................................. 3 3 Matrices: addition and multiplication . 4 4 Thetransposeofamatrix ..................... 6 5 Squarematrices........................... 6 6 Linearformsandquadraticforms. 7 7 Therankofamatrix........................ 9 8 Theinverse ............................. 10 9 Thedeterminant .......................... 10 10 Thetrace .............................. 11 11 Partitionedmatrices ........................ 12 12 Complexmatrices ......................... 14 13 Eigenvaluesandeigenvectors . 14 14 Schur’sdecompositiontheorem . 17 15 TheJordandecomposition. 18 16 Thesingular-valuedecomposition . 20 17 Furtherresultsconcerningeigenvalues . 20 18 Positive(semi)definitematrices . 23 19 Three further results for positive definite matrices . 25 20 Ausefulresult ........................... 26 21 Symmetricmatrixfunctions . 27 Miscellaneous exercises .......................... 28 Bibliographical notes ........................... 30 2 Kronecker products, vec operator, and Moore-Penrose inverse 31 1 Introduction............................. 31 2 TheKroneckerproduct ...................... 31 3 EigenvaluesofaKroneckerproduct. 33 4 Thevecoperator .......................... 34 5 TheMoore-Penrose(MP)inverse . 36 v vi Contents 6 ExistenceanduniquenessoftheMPinverse . 37 7 SomepropertiesoftheMPinverse . 38 8 Furtherproperties ......................... 39 9 The solution of linear equation systems . 41 Miscellaneous exercises .......................... 43 Bibliographical notes ........................... 45 3 Miscellaneous matrix results 47 1 Introduction............................. 47 2 Theadjointmatrix......................... 47 3 ProofofTheorem3.1........................ 49 4 Bordereddeterminants. .. .. .. .. .. .. .. .. .. 51 5 The matrix equation AX =0 ................... 51 6 TheHadamardproduct ...................... 52 7 The commutation matrix Kmn .................. 54 8 The duplication matrix Dn .................... 56 9 Relationship between Dn+1 and Dn, I .............. 58 10 Relationship between Dn+1 and Dn, II.............. 59 11 Conditions for a quadratic form to be positive (negative) subjecttolinearconstraints . 60 12 Necessary and sufficient conditions for r(A : B)= r(A)+ r(B) 63 13 TheborderedGramianmatrix . 65 14 The equations X1A + X2B′ = G1,X1B = G2 .......... 67 Miscellaneous exercises .......................... 69 Bibliographical notes ........................... 70 Part Two — Differentials: the theory 4 Mathematical preliminaries 73 1 Introduction............................. 73 2 Interiorpointsandaccumulationpoints . 73 3 Openandclosedsets........................ 75 4 TheBolzano-Weierstrasstheorem. 77 5 Functions .............................. 78 6 Thelimitofafunction....................... 79 7 Continuousfunctionsandcompactness . 80 8 Convexsets............................. 81 9 Convexandconcavefunctions. 83 Bibliographical notes ........................... 86 5 Differentials and differentiability 87 1 Introduction............................. 87 2 Continuity.............................. 88 3 Differentiability and linear approximation . 90 4 Thedifferentialofavectorfunction. 91 5 Uniquenessofthedifferential . 93 6 Continuity of differentiable functions . 94 Contents vii 7 Partialderivatives ......................... 95 8 Thefirstidentificationtheorem . 96 9 Existenceofthedifferential,I . 97 10 Existenceofthedifferential,II . 99 11 Continuous differentiability . 100 12 Thechainrule ...........................100 13 Cauchyinvariance .........................102 14 The mean-value theorem for real-valued functions . 103 15 Differentiablematrixfunctions . 104 16 Someremarksonnotation. .106 17 Complexdifferentiation . .108 Miscellaneous exercises ..........................110 Bibliographical notes ...........................110 6 The second differential 111 1 Introduction.............................111 2 Second-orderpartialderivatives . 111 3 TheHessianmatrix.........................112 4 Twice differentiability and second-order approximation, I . 113 5 Definition of twice differentiability . 114 6 Theseconddifferential.. .. .. .. .. .. .. .. .. ..115 7 SymmetryoftheHessianmatrix . .117 8 Thesecondidentificationtheorem . 119 9 Twice differentiability and second-order approximation, II . 119 10 ChainruleforHessianmatrices . 121 11 Theanalogforseconddifferentials . 123 12 Taylor’stheoremforreal-valuedfunctions . 124 13 Higher-orderdifferentials. .125 14 Realanalyticfunctions. .125 15 Twice differentiable matrix functions . 126 Bibliographical notes ...........................127 7 Static optimization 129 1 Introduction.............................129 2 Unconstrainedoptimization . .130 3 Theexistenceofabsoluteextrema . 131 4 Necessaryconditionsforalocalminimum . 132 5 Sufficient conditions for a local minimum: first-derivative test . 134 6 Sufficient conditions for a local minimum: second-derivative test 136 7 Characterization of differentiable convex functions . 138 8 Characterization of twice differentiable convex functions . 141 9 Sufficient conditions for an absolute minimum
Load more

Recommended publications
  • Mathematics for Dynamicists - Lecture Notes Thomas Michelitsch
    Mathematics for Dynamicists - Lecture Notes Thomas Michelitsch To cite this version: Thomas Michelitsch. Mathematics for Dynamicists - Lecture Notes. Doctoral. Mathematics for Dynamicists, France. 2006. cel-01128826 HAL Id: cel-01128826 https://hal.archives-ouvertes.fr/cel-01128826 Submitted on 10 Mar 2015 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Mathematics for Dynamicists Lecture Notes c 2004-2006 Thomas Michael Michelitsch1 Department of Civil and Structural Engineering The University of Sheffield Sheffield, UK 1Present address : http://www.dalembert.upmc.fr/home/michelitsch/ . Dedicated to the memory of my parents Michael and Hildegard Michelitsch Handout Manuscript with Fractal Cover Picture by Michael Michelitsch https://www.flickr.com/photos/michelitsch/sets/72157601230117490 1 Contents Preface 1 Part I 1.1 Binomial Theorem 1.2 Derivatives, Integrals and Taylor Series 1.3 Elementary Functions 1.4 Complex Numbers: Cartesian and Polar Representation 1.5 Sequences, Series, Integrals and Power-Series 1.6 Polynomials and Partial Fractions
    [Show full text]
  • Block Kronecker Products and the Vecb Operator* CORE View
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Block Kronecker Products and the vecb Operator* Ruud H. Koning Department of Economics University of Groningen P.O. Box 800 9700 AV, Groningen, The Netherlands Heinz Neudecker+ Department of Actuarial Sciences and Econometrics University of Amsterdam Jodenbreestraat 23 1011 NH, Amsterdam, The Netherlands and Tom Wansbeek Department of Economics University of Groningen P.O. Box 800 9700 AV, Groningen, The Netherlands Submitted hv Richard Rrualdi ABSTRACT This paper is concerned with two generalizations of the Kronecker product and two related generalizations of the vet operator. It is demonstrated that they pairwise match two different kinds of matrix partition, viz. the balanced and unbalanced ones. Relevant properties are supplied and proved. A related concept, the so-called tilde transform of a balanced block matrix, is also studied. The results are illustrated with various statistical applications of the five concepts studied. *Comments of an anonymous referee are gratefully acknowledged. ‘This work was started while the second author was at the Indian Statistiral Institute, New Delhi. LINEAR ALGEBRA AND ITS APPLICATIONS 149:165-184 (1991) 165 0 Elsevier Science Publishing Co., Inc., 1991 655 Avenue of the Americas, New York, NY 10010 0024-3795/91/$3.50 166 R. H. KONING, H. NEUDECKER, AND T. WANSBEEK INTRODUCTION Almost twenty years ago Singh [7] and Tracy and Singh [9] introduced a generalization of the Kronecker product A@B. They used varying notation for this new product, viz. A @ B and A &3B. Recently, Hyland and Collins [l] studied the-same product under rather restrictive order conditions.
    [Show full text]
  • The Mean Value Theorem Math 120 Calculus I Fall 2015
    The Mean Value Theorem Math 120 Calculus I Fall 2015 The central theorem to much of differential calculus is the Mean Value Theorem, which we'll abbreviate MVT. It is the theoretical tool used to study the first and second derivatives. There is a nice logical sequence of connections here. It starts with the Extreme Value Theorem (EVT) that we looked at earlier when we studied the concept of continuity. It says that any function that is continuous on a closed interval takes on a maximum and a minimum value. A technical lemma. We begin our study with a technical lemma that allows us to relate 0 the derivative of a function at a point to values of the function nearby. Specifically, if f (x0) is positive, then for x nearby but smaller than x0 the values f(x) will be less than f(x0), but for x nearby but larger than x0, the values of f(x) will be larger than f(x0). This says something like f is an increasing function near x0, but not quite. An analogous statement 0 holds when f (x0) is negative. Proof. The proof of this lemma involves the definition of derivative and the definition of limits, but none of the proofs for the rest of the theorems here require that depth. 0 Suppose that f (x0) = p, some positive number. That means that f(x) − f(x ) lim 0 = p: x!x0 x − x0 f(x) − f(x0) So you can make arbitrarily close to p by taking x sufficiently close to x0.
    [Show full text]
  • AP Calculus AB Topic List 1. Limits Algebraically 2. Limits Graphically 3
    AP Calculus AB Topic List 1. Limits algebraically 2. Limits graphically 3. Limits at infinity 4. Asymptotes 5. Continuity 6. Intermediate value theorem 7. Differentiability 8. Limit definition of a derivative 9. Average rate of change (approximate slope) 10. Tangent lines 11. Derivatives rules and special functions 12. Chain Rule 13. Application of chain rule 14. Derivatives of generic functions using chain rule 15. Implicit differentiation 16. Related rates 17. Derivatives of inverses 18. Logarithmic differentiation 19. Determine function behavior (increasing, decreasing, concavity) given a function 20. Determine function behavior (increasing, decreasing, concavity) given a derivative graph 21. Interpret first and second derivative values in a table 22. Determining if tangent line approximations are over or under estimates 23. Finding critical points and determining if they are relative maximum, relative minimum, or neither 24. Second derivative test for relative maximum or minimum 25. Finding inflection points 26. Finding and justifying critical points from a derivative graph 27. Absolute maximum and minimum 28. Application of maximum and minimum 29. Motion derivatives 30. Vertical motion 31. Mean value theorem 32. Approximating area with rectangles and trapezoids given a function 33. Approximating area with rectangles and trapezoids given a table of values 34. Determining if area approximations are over or under estimates 35. Finding definite integrals graphically 36. Finding definite integrals using given integral values 37. Indefinite integrals with power rule or special derivatives 38. Integration with u-substitution 39. Evaluating definite integrals 40. Definite integrals with u-substitution 41. Solving initial value problems (separable differential equations) 42. Creating a slope field 43.
    [Show full text]
  • Genius Manual I
    Genius Manual i Genius Manual Genius Manual ii Copyright © 1997-2016 Jiríˇ (George) Lebl Copyright © 2004 Kai Willadsen Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License (GFDL), Version 1.1 or any later version published by the Free Software Foundation with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. You can find a copy of the GFDL at this link or in the file COPYING-DOCS distributed with this manual. This manual is part of a collection of GNOME manuals distributed under the GFDL. If you want to distribute this manual separately from the collection, you can do so by adding a copy of the license to the manual, as described in section 6 of the license. Many of the names used by companies to distinguish their products and services are claimed as trademarks. Where those names appear in any GNOME documentation, and the members of the GNOME Documentation Project are made aware of those trademarks, then the names are in capital letters or initial capital letters. DOCUMENT AND MODIFIED VERSIONS OF THE DOCUMENT ARE PROVIDED UNDER THE TERMS OF THE GNU FREE DOCUMENTATION LICENSE WITH THE FURTHER UNDERSTANDING THAT: 1. DOCUMENT IS PROVIDED ON AN "AS IS" BASIS, WITHOUT WARRANTY OF ANY KIND, EITHER EXPRESSED OR IMPLIED, INCLUDING, WITHOUT LIMITATION, WARRANTIES THAT THE DOCUMENT OR MODIFIED VERSION OF THE DOCUMENT IS FREE OF DEFECTS MERCHANTABLE, FIT FOR A PARTICULAR PURPOSE OR NON-INFRINGING. THE ENTIRE RISK AS TO THE QUALITY, ACCURACY, AND PERFORMANCE OF THE DOCUMENT OR MODIFIED VERSION OF THE DOCUMENT IS WITH YOU.
    [Show full text]
  • Multivariable and Vector Calculus
    Multivariable and Vector Calculus Lecture Notes for MATH 0200 (Spring 2015) Frederick Tsz-Ho Fong Department of Mathematics Brown University Contents 1 Three-Dimensional Space ....................................5 1.1 Rectangular Coordinates in R3 5 1.2 Dot Product7 1.3 Cross Product9 1.4 Lines and Planes 11 1.5 Parametric Curves 13 2 Partial Differentiations ....................................... 19 2.1 Functions of Several Variables 19 2.2 Partial Derivatives 22 2.3 Chain Rule 26 2.4 Directional Derivatives 30 2.5 Tangent Planes 34 2.6 Local Extrema 36 2.7 Lagrange’s Multiplier 41 2.8 Optimizations 46 3 Multiple Integrations ........................................ 49 3.1 Double Integrals in Rectangular Coordinates 49 3.2 Fubini’s Theorem for General Regions 53 3.3 Double Integrals in Polar Coordinates 57 3.4 Triple Integrals in Rectangular Coordinates 62 3.5 Triple Integrals in Cylindrical Coordinates 67 3.6 Triple Integrals in Spherical Coordinates 70 4 Vector Calculus ............................................ 75 4.1 Vector Fields on R2 and R3 75 4.2 Line Integrals of Vector Fields 83 4.3 Conservative Vector Fields 88 4.4 Green’s Theorem 98 4.5 Parametric Surfaces 105 4.6 Stokes’ Theorem 120 4.7 Divergence Theorem 127 5 Topics in Physics and Engineering .......................... 133 5.1 Coulomb’s Law 133 5.2 Introduction to Maxwell’s Equations 137 5.3 Heat Diffusion 141 5.4 Dirac Delta Functions 144 1 — Three-Dimensional Space 1.1 Rectangular Coordinates in R3 Throughout the course, we will use an ordered triple (x, y, z) to represent a point in the three dimensional space.
    [Show full text]
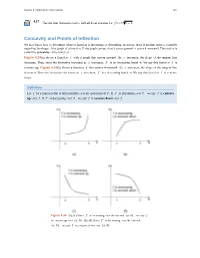
  • Concavity and Points of Inflection We Now Know How to Determine Where a Function Is Increasing Or Decreasing
    Chapter 4 | Applications of Derivatives 401 4.17 3 Use the first derivative test to find all local extrema for f (x) = x − 1. Concavity and Points of Inflection We now know how to determine where a function is increasing or decreasing. However, there is another issue to consider regarding the shape of the graph of a function. If the graph curves, does it curve upward or curve downward? This notion is called the concavity of the function. Figure 4.34(a) shows a function f with a graph that curves upward. As x increases, the slope of the tangent line increases. Thus, since the derivative increases as x increases, f ′ is an increasing function. We say this function f is concave up. Figure 4.34(b) shows a function f that curves downward. As x increases, the slope of the tangent line decreases. Since the derivative decreases as x increases, f ′ is a decreasing function. We say this function f is concave down. Definition Let f be a function that is differentiable over an open interval I. If f ′ is increasing over I, we say f is concave up over I. If f ′ is decreasing over I, we say f is concave down over I. Figure 4.34 (a), (c) Since f ′ is increasing over the interval (a, b), we say f is concave up over (a, b). (b), (d) Since f ′ is decreasing over the interval (a, b), we say f is concave down over (a, b). 402 Chapter 4 | Applications of Derivatives In general, without having the graph of a function f , how can we determine its concavity? By definition, a function f is concave up if f ′ is increasing.
    [Show full text]
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]
  • Package 'Fastmatrix'
    Package ‘fastmatrix’ May 8, 2021 Type Package Title Fast Computation of some Matrices Useful in Statistics Version 0.3-819 Date 2021-05-07 Author Felipe Osorio [aut, cre] (<https://orcid.org/0000-0002-4675-5201>), Alonso Ogueda [aut] Maintainer Felipe Osorio <[email protected]> Description Small set of functions to fast computation of some matrices and operations useful in statistics and econometrics. Currently, there are functions for efficient computation of duplication, commutation and symmetrizer matrices with minimal storage requirements. Some commonly used matrix decompositions (LU and LDL), basic matrix operations (for instance, Hadamard, Kronecker products and the Sherman-Morrison formula) and iterative solvers for linear systems are also available. In addition, the package includes a number of common statistical procedures such as the sweep operator, weighted mean and covariance matrix using an online algorithm, linear regression (using Cholesky, QR, SVD, sweep operator and conjugate gradients methods), ridge regression (with optimal selection of the ridge parameter considering the GCV procedure), functions to compute the multivariate skewness, kurtosis, Mahalanobis distance (checking the positive defineteness) and the Wilson-Hilferty transformation of chi squared variables. Furthermore, the package provides interfaces to C code callable by another C code from other R packages. Depends R(>= 3.5.0) License GPL-3 URL https://faosorios.github.io/fastmatrix/ NeedsCompilation yes LazyLoad yes Repository CRAN Date/Publication 2021-05-08 08:10:06 UTC R topics documented: array.mult . .3 1 2 R topics documented: asSymmetric . .4 bracket.prod . .5 cg ..............................................6 comm.info . .7 comm.prod . .8 commutation . .9 cov.MSSD . 10 cov.weighted .
    [Show full text]
  • Matrix Calculus
    Appendix D Matrix Calculus From too much study, and from extreme passion, cometh madnesse. Isaac Newton [205, §5] − D.1 Gradient, Directional derivative, Taylor series D.1.1 Gradients Gradient of a differentiable real function f(x) : RK R with respect to its vector argument is defined uniquely in terms of partial derivatives→ ∂f(x) ∂x1 ∂f(x) , ∂x2 RK f(x) . (2053) ∇ . ∈ . ∂f(x) ∂xK while the second-order gradient of the twice differentiable real function with respect to its vector argument is traditionally called the Hessian; 2 2 2 ∂ f(x) ∂ f(x) ∂ f(x) 2 ∂x1 ∂x1∂x2 ··· ∂x1∂xK 2 2 2 ∂ f(x) ∂ f(x) ∂ f(x) 2 2 K f(x) , ∂x2∂x1 ∂x2 ··· ∂x2∂xK S (2054) ∇ . ∈ . .. 2 2 2 ∂ f(x) ∂ f(x) ∂ f(x) 2 ∂xK ∂x1 ∂xK ∂x2 ∂x ··· K interpreted ∂f(x) ∂f(x) 2 ∂ ∂ 2 ∂ f(x) ∂x1 ∂x2 ∂ f(x) = = = (2055) ∂x1∂x2 ³∂x2 ´ ³∂x1 ´ ∂x2∂x1 Dattorro, Convex Optimization Euclidean Distance Geometry, Mεβoo, 2005, v2020.02.29. 599 600 APPENDIX D. MATRIX CALCULUS The gradient of vector-valued function v(x) : R RN on real domain is a row vector → v(x) , ∂v1(x) ∂v2(x) ∂vN (x) RN (2056) ∇ ∂x ∂x ··· ∂x ∈ h i while the second-order gradient is 2 2 2 2 , ∂ v1(x) ∂ v2(x) ∂ vN (x) RN v(x) 2 2 2 (2057) ∇ ∂x ∂x ··· ∂x ∈ h i Gradient of vector-valued function h(x) : RK RN on vector domain is → ∂h1(x) ∂h2(x) ∂hN (x) ∂x1 ∂x1 ··· ∂x1 ∂h1(x) ∂h2(x) ∂hN (x) h(x) , ∂x2 ∂x2 ··· ∂x2 ∇ .
    [Show full text]
  • Matrix Calculus
    D Matrix Calculus D–1 Appendix D: MATRIX CALCULUS D–2 In this Appendix we collect some useful formulas of matrix calculus that often appear in finite element derivations. §D.1 THE DERIVATIVES OF VECTOR FUNCTIONS Let x and y be vectors of orders n and m respectively: x1 y1 x2 y2 x = . , y = . ,(D.1) . xn ym where each component yi may be a function of all the xj , a fact represented by saying that y is a function of x,or y = y(x). (D.2) If n = 1, x reduces to a scalar, which we call x.Ifm = 1, y reduces to a scalar, which we call y. Various applications are studied in the following subsections. §D.1.1 Derivative of Vector with Respect to Vector The derivative of the vector y with respect to vector x is the n × m matrix ∂y1 ∂y2 ∂ym ∂ ∂ ··· ∂ x1 x1 x1 ∂ ∂ ∂ ∂ y1 y2 ··· ym y def ∂x ∂x ∂x = 2 2 2 (D.3) ∂x . . .. ∂ ∂ ∂ y1 y2 ··· ym ∂xn ∂xn ∂xn §D.1.2 Derivative of a Scalar with Respect to Vector If y is a scalar, ∂y ∂x1 ∂ ∂ y y def ∂ = x2 .(D.4) ∂x . . ∂y ∂xn §D.1.3 Derivative of Vector with Respect to Scalar If x is a scalar, ∂y def ∂ ∂ ∂ = y1 y2 ... ym (D.5) ∂x ∂x ∂x ∂x D–2 D–3 §D.1 THE DERIVATIVES OF VECTOR FUNCTIONS REMARK D.1 Many authors, notably in statistics and economics, define the derivatives as the transposes of those given above.1 This has the advantage of better agreement of matrix products with composition schemes such as the chain rule.
    [Show full text]
  • Dynamics of Correlation Structure in Stock Market
    Entropy 2014, 16, 455-470; doi:10.3390/e16010455 OPEN ACCESS entropy ISSN 1099-4300 www.mdpi.com/journal/entropy Article Dynamics of Correlation Structure in Stock Market Maman Abdurachman Djauhari * and Siew Lee Gan Department of Mathematical Sciences, Faculty of Science, Universiti Teknologi Malaysia, 81310 UTM Skudai, Johor Bahru, Johor Darul Takzim, Malaysia; E-Mail: [email protected] * Author to whom correspondence should be addressed; E-Mail: [email protected]; Tel.: +60-017-520-0795; Fax: +60-07-556-6162. Received: 24 September 2013; in revised form: 19 December 2013 / Accepted: 24 December 2013 / Published: 6 January 2014 Abstract: In this paper a correction factor for Jennrich’s statistic is introduced in order to be able not only to test the stability of correlation structure, but also to identify the time windows where the instability occurs. If Jennrich’s statistic is only to test the stability of correlation structure along predetermined non-overlapping time windows, the corrected statistic provides us with the history of correlation structure dynamics from time window to time window. A graphical representation will be provided to visualize that history. This information is necessary to make further analysis about, for example, the change of topological properties of minimal spanning tree. An example using NYSE data will illustrate its advantages. Keywords: Mahalanobis square distance; multivariate normal distribution; network topology; Pearson correlation coefficient; random matrix PACS Codes: 89.65.Gh; 89.75.Fb 1. Introduction Correlation structure among stocks in a given portfolio is a complex structure represented numerically in the form of a symmetric matrix where all diagonal elements are equal to 1 and the off-diagonals are the correlations of two different stocks.
    [Show full text]