Information Theory and Predictability. Lecture 4: Optimal Codes
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Compilers & Translator Writing Systems
Compilers & Translators Compilers & Translator Writing Systems Prof. R. Eigenmann ECE573, Fall 2005 http://www.ece.purdue.edu/~eigenman/ECE573 ECE573, Fall 2005 1 Compilers are Translators Fortran Machine code C Virtual machine code C++ Transformed source code Java translate Augmented source Text processing language code Low-level commands Command Language Semantic components Natural language ECE573, Fall 2005 2 ECE573, Fall 2005, R. Eigenmann 1 Compilers & Translators Compilers are Increasingly Important Specification languages Increasingly high level user interfaces for ↑ specifying a computer problem/solution High-level languages ↑ Assembly languages The compiler is the translator between these two diverging ends Non-pipelined processors Pipelined processors Increasingly complex machines Speculative processors Worldwide “Grid” ECE573, Fall 2005 3 Assembly code and Assemblers assembly machine Compiler code Assembler code Assemblers are often used at the compiler back-end. Assemblers are low-level translators. They are machine-specific, and perform mostly 1:1 translation between mnemonics and machine code, except: – symbolic names for storage locations • program locations (branch, subroutine calls) • variable names – macros ECE573, Fall 2005 4 ECE573, Fall 2005, R. Eigenmann 2 Compilers & Translators Interpreters “Execute” the source language directly. Interpreters directly produce the result of a computation, whereas compilers produce executable code that can produce this result. Each language construct executes by invoking a subroutine of the interpreter, rather than a machine instruction. Examples of interpreters? ECE573, Fall 2005 5 Properties of Interpreters “execution” is immediate elaborate error checking is possible bookkeeping is possible. E.g. for garbage collection can change program on-the-fly. E.g., switch libraries, dynamic change of data types machine independence. -

Chapter 2 Basics of Scanning And
Chapter 2 Basics of Scanning and Conventional Programming in Java In this chapter, we will introduce you to an initial set of Java features, the equivalent of which you should have seen in your CS-1 class; the separation of problem, representation, algorithm and program – four concepts you have probably seen in your CS-1 class; style rules with which you are probably familiar, and scanning - a general class of problems we see in both computer science and other fields. Each chapter is associated with an animating recorded PowerPoint presentation and a YouTube video created from the presentation. It is meant to be a transcript of the associated presentation that contains little graphics and thus can be read even on a small device. You should refer to the associated material if you feel the need for a different instruction medium. Also associated with each chapter is hyperlinked code examples presented here. References to previously presented code modules are links that can be traversed to remind you of the details. The resources for this chapter are: PowerPoint Presentation YouTube Video Code Examples Algorithms and Representation Four concepts we explicitly or implicitly encounter while programming are problems, representations, algorithms and programs. Programs, of course, are instructions executed by the computer. Problems are what we try to solve when we write programs. Usually we do not go directly from problems to programs. Two intermediate steps are creating algorithms and identifying representations. Algorithms are sequences of steps to solve problems. So are programs. Thus, all programs are algorithms but the reverse is not true. -

Scripting: Higher- Level Programming for the 21St Century
. John K. Ousterhout Sun Microsystems Laboratories Scripting: Higher- Cybersquare Level Programming for the 21st Century Increases in computer speed and changes in the application mix are making scripting languages more and more important for the applications of the future. Scripting languages differ from system programming languages in that they are designed for “gluing” applications together. They use typeless approaches to achieve a higher level of programming and more rapid application development than system programming languages. or the past 15 years, a fundamental change has been ated with system programming languages and glued Foccurring in the way people write computer programs. together with scripting languages. However, several The change is a transition from system programming recent trends, such as faster machines, better script- languages such as C or C++ to scripting languages such ing languages, the increasing importance of graphical as Perl or Tcl. Although many people are participat- user interfaces (GUIs) and component architectures, ing in the change, few realize that the change is occur- and the growth of the Internet, have greatly expanded ring and even fewer know why it is happening. This the applicability of scripting languages. These trends article explains why scripting languages will handle will continue over the next decade, with more and many of the programming tasks in the next century more new applications written entirely in scripting better than system programming languages. languages and system programming -

The Future of DNA Data Storage the Future of DNA Data Storage
The Future of DNA Data Storage The Future of DNA Data Storage September 2018 A POTOMAC INSTITUTE FOR POLICY STUDIES REPORT AC INST M IT O U T B T The Future O E P F O G S R IE of DNA P D O U Data LICY ST Storage September 2018 NOTICE: This report is a product of the Potomac Institute for Policy Studies. The conclusions of this report are our own, and do not necessarily represent the views of our sponsors or participants. Many thanks to the Potomac Institute staff and experts who reviewed and provided comments on this report. © 2018 Potomac Institute for Policy Studies Cover image: Alex Taliesen POTOMAC INSTITUTE FOR POLICY STUDIES 901 North Stuart St., Suite 1200 | Arlington, VA 22203 | 703-525-0770 | www.potomacinstitute.org CONTENTS EXECUTIVE SUMMARY 4 Findings 5 BACKGROUND 7 Data Storage Crisis 7 DNA as a Data Storage Medium 9 Advantages 10 History 11 CURRENT STATE OF DNA DATA STORAGE 13 Technology of DNA Data Storage 13 Writing Data to DNA 13 Reading Data from DNA 18 Key Players in DNA Data Storage 20 Academia 20 Research Consortium 21 Industry 21 Start-ups 21 Government 22 FORECAST OF DNA DATA STORAGE 23 DNA Synthesis Cost Forecast 23 Forecast for DNA Data Storage Tech Advancement 28 Increasing Data Storage Density in DNA 29 Advanced Coding Schemes 29 DNA Sequencing Methods 30 DNA Data Retrieval 31 CONCLUSIONS 32 ENDNOTES 33 Executive Summary The demand for digital data storage is currently has been developed to support applications in outpacing the world’s storage capabilities, and the life sciences industry and not for data storage the gap is widening as the amount of digital purposes. -

How Do You Know Your Search Algorithm and Code Are Correct?
Proceedings of the Seventh Annual Symposium on Combinatorial Search (SoCS 2014) How Do You Know Your Search Algorithm and Code Are Correct? Richard E. Korf Computer Science Department University of California, Los Angeles Los Angeles, CA 90095 [email protected] Abstract Is a Given Solution Correct? Algorithm design and implementation are notoriously The first question to ask of a search algorithm is whether the error-prone. As researchers, it is incumbent upon us to candidate solutions it returns are valid solutions. The algo- maximize the probability that our algorithms, their im- rithm should output each solution, and a separate program plementations, and the results we report are correct. In should check its correctness. For any problem in NP, check- this position paper, I argue that the main technique for ing candidate solutions can be done in polynomial time. doing this is confirmation of results from multiple in- dependent sources, and provide a number of concrete Is a Given Solution Optimal? suggestions for how to achieve this in the context of combinatorial search algorithms. Next we consider whether the solutions returned are opti- mal. In most cases, there are multiple very different algo- rithms that compute optimal solutions, starting with sim- Introduction and Overview ple brute-force algorithms, and progressing through increas- Combinatorial search results can be theoretical or experi- ingly complex and more efficient algorithms. Thus, one can mental. Theoretical results often consist of correctness, com- compare the solution costs returned by the different algo- pleteness, the quality of solutions returned, and asymptotic rithms, which should all be the same. -
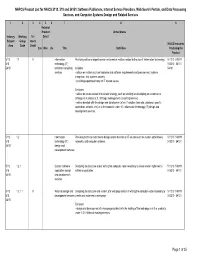
NAPCS Product List for NAICS 5112, 518 and 54151: Software
NAPCS Product List for NAICS 5112, 518 and 54151: Software Publishers, Internet Service Providers, Web Search Portals, and Data Processing Services, and Computer Systems Design and Related Services 1 2 3 456 7 8 9 National Product United States Industry Working Tri- Detail Subject Group lateral NAICS Industries Area Code Detail Can Méx US Title Definition Producing the Product 5112 1.1 X Information Providing advice or expert opinion on technical matters related to the use of information technology. 511210 518111 518 technology (IT) 518210 54151 54151 technical consulting Includes: 54161 services • advice on matters such as hardware and software requirements and procurement, systems integration, and systems security. • providing expert testimony on IT related issues. Excludes: • advice on issues related to business strategy, such as advising on developing an e-commerce strategy, is in product 2.3, Strategic management consulting services. • advice bundled with the design and development of an IT solution (web site, database, specific application, network, etc.) is in the products under 1.2, Information technology (IT) design and development services. 5112 1.2 Information Providing technical expertise to design and/or develop an IT solution such as custom applications, 511210 518111 518 technology (IT) networks, and computer systems. 518210 54151 54151 design and development services 5112 1.2.1 Custom software Designing the structure and/or writing the computer code necessary to create and/or implement a 511210 518111 518 application design software application. 518210 54151 54151 and development services 5112 1.2.1.1 X Web site design and Designing the structure and content of a web page and/or of writing the computer code necessary to 511210 518111 518 development services create and implement a web page. -

Media Theory and Semiotics: Key Terms and Concepts Binary
Media Theory and Semiotics: Key Terms and Concepts Binary structures and semiotic square of oppositions Many systems of meaning are based on binary structures (masculine/ feminine; black/white; natural/artificial), two contrary conceptual categories that also entail or presuppose each other. Semiotic interpretation involves exposing the culturally arbitrary nature of this binary opposition and describing the deeper consequences of this structure throughout a culture. On the semiotic square and logical square of oppositions. Code A code is a learned rule for linking signs to their meanings. The term is used in various ways in media studies and semiotics. In communication studies, a message is often described as being "encoded" from the sender and then "decoded" by the receiver. The encoding process works on multiple levels. For semiotics, a code is the framework, a learned a shared conceptual connection at work in all uses of signs (language, visual). An easy example is seeing the kinds and levels of language use in anyone's language group. "English" is a convenient fiction for all the kinds of actual versions of the language. We have formal, edited, written English (which no one speaks), colloquial, everyday, regional English (regions in the US, UK, and around the world); social contexts for styles and specialized vocabularies (work, office, sports, home); ethnic group usage hybrids, and various kinds of slang (in-group, class-based, group-based, etc.). Moving among all these is called "code-switching." We know what they mean if we belong to the learned, rule-governed, shared-code group using one of these kinds and styles of language. -

Decoder-Tailored Polar Code Design Using the Genetic Algorithm
Decoder-tailored Polar Code Design Using the Genetic Algorithm Ahmed Elkelesh, Moustafa Ebada, Sebastian Cammerer and Stephan ten Brink Abstract—We propose a new framework for constructing a slight negligible performance degradation. The concatenation polar codes (i.e., selecting the frozen bit positions) for arbitrary with an additional high-rate Cyclic Redundancy Check (CRC) channels, and tailored to a given decoding algorithm, rather than code [4] or parity-check (PC) code [6] further improves the based on the (not necessarily optimal) assumption of successive cancellation (SC) decoding. The proposed framework is based code performance itself, as it increases the minimum distance on the Genetic Algorithm (GenAlg), where populations (i.e., and, thus, improves the weight spectrum of the code. This collections) of information sets evolve successively via evolu- simple concatenation renders polar codes into a powerful tionary transformations based on their individual error-rate coding scheme. For short length codes [7], polar codes were performance. These populations converge towards an information recently selected by the 3GPP group as the channel codes for set that fits both the decoding behavior and the defined channel. Using our proposed algorithm over the additive white Gaussian the upcoming 5th generation mobile communication standard noise (AWGN) channel, we construct a polar code of length (5G) uplink/downlink control channel [8]. 2048 with code rate 0:5, without the CRC-aid, tailored to plain On the other hand, some drawbacks can be seen in their high successive cancellation list (SCL) decoding, achieving the same decoding complexity and large latency for long block lengths error-rate performance as the CRC-aided SCL decoding, and 6 under SCL decoding due to their inherent sequential decoding leading to a coding gain of 1dB at BER of 10− . -

Professional and Ethical Compliance Code for Behavior Analysts
BEHAVIOR ANALYST CERTIFICATION BOARD® = Professional and Ethical ® Compliance Code for = Behavior Analysts The Behavior Analyst Certification Board’s (BACB’s) Professional and Ethical Compliance Code for Behavior Analysts (the “Code”) consolidates, updates, and replaces the BACB’s Professional Disciplinary and Ethical Standards and Guidelines for Responsible Conduct for Behavior Analysts. The Code includes 10 sections relevant to professional and ethical behavior of behavior analysts, along with a glossary of terms. Effective January 1, 2016, all BACB applicants and certificants will be required to adhere to the Code. _________________________ In the original version of the Guidelines for Professional Conduct for Behavior Analysts, the authors acknowledged ethics codes from the following organizations: American Anthropological Association, American Educational Research Association, American Psychological Association, American Sociological Association, California Association for Behavior Analysis, Florida Association for Behavior Analysis, National Association of Social Workers, National Association of School Psychologists, and Texas Association for Behavior Analysis. We acknowledge and thank these professional organizations that have provided substantial guidance and clear models from which the Code has evolved. Approved by the BACB’s Board of Directors on August 7, 2014. This document should be referenced as: Behavior Analyst Certification Board. (2014). Professional and ethical compliance code for behavior analysts. Littleton, CO: Author. -

Variations and Evolution of the Elian Script
1 EVOLUTION OF THE ELIAN SCRIPT From Code to Calligraphic Writing System. How this: Evolved into this… THE E LIAN S CRIPT - EVOLUTIONS AND VARIATIONS 2 Then into this: The Elian script was originally intended to differentiate, at a glance, unfinished notebook writings from those still in progress. Before developing this system I used the letters of the Cyrillic alphabet as sheer phonetic elements: "Tuscany" would thus be written " ". The more I wrote phonetically in Cyrillic, however, the more my spelling in English deteriorated - " " back to English would be written "Tskani;” I needed something else. Soon after, I came across the numbered nine-square grid (page 3). It occurred to me that each of the nine boxes had a unique configuration, and that with the addition of a numeral, "1", "2", or "3", it was possible to have a coded form for each of the 26 letters of the Latin alphabet. At first I used this grid simply as a code since its initial form had no calligraphic aspects to it. Only when modification led to modification did the potential for calligraphy emerge. THE E LIAN S CRIPT - EVOLUTIONS AND VARIATIONS 3 Below is an outline of the code’s structure, followed by a series of illustrations that show its formal evolution from code to calligraphic writing system1. The starting point of the Elian script was a one-to-one code written in the same sequence as the letters that it codified: “years. What” The boxes above with a numeral from 1-3 in them each refer to one specific letter out of a possible three, in keeping with the system shown below: Each box inside the nine-square grid is unique in shape, such that a set of box coordinates can refer to only one of the nine boxes2. -

An Improved Algorithm for Solving Code Equivalence Problems Over Fq
Not enough LESS: An improved algorithm for solving Code Equivalence Problems over Fq Ward Beullens1 imec-COSIC, KU Leuven [email protected] Abstract. Recently, a new code based signature scheme, called LESS, was proposed with three concrete instantiations, each aiming to provide 128 bits of classical security [3]. Two instantiations (LESS-I and LESS- II) are based on the conjectured hardness of the linear code equivalence problem, while a third instantiation, LESS-III, is based on the conjec- tured hardness of the permutation code equivalence problem for weakly self-dual codes. We give an improved algorithm for solving both these problems over sufficiently large finite fields. Our implementation breaks LESS-I and LESS-III in approximately 25 seconds and 2 seconds respec- tively on a laptop. Since the field size for LESS-II is relatively small (F7) our algorithm does not improve on existing methods. Nonetheless, we estimate that LESS-II can be broken with approximately 244 row operations. Keywords: permutation code equivalence problem, linear code equivalence prob- lem, code-based cryptography, post-quantum cryptography 1 Introduction Two q-ary linear codes C1 and C2 of length n and dimension k are called per- mutation equivalent if there exists a permutation π 2 Sn such that π(C1) = C2. × n Similarly, if there exists a monomial permutation µ 2 Mn = (Fq ) n Sn such that µ(C1) = C2 the codes are said to be linearly equivalent (a monomial per- n mutation acts on vectors in Fq by permuting the entries and also multiplying each entry with a unit of Fq). -

ICU and Writing Systems Ken Zook June 20, 2014 Contents 1 ICU Introduction
ICU and writing systems Ken Zook June 20, 2014 Contents 1 ICU introduction .......................................................................................................... 1 2 ICU files ...................................................................................................................... 2 2.1 unidata .................................................................................................................. 3 2.2 locales ................................................................................................................... 3 2.3 coll ........................................................................................................................ 4 3 Languages and dialects ................................................................................................ 4 4 Writing systems in FieldWorks ................................................................................... 5 5 InstallLanguage ........................................................................................................... 8 6 Writing systems during FieldWorks installation ......................................................... 9 7 Custom Character setup ............................................................................................... 9 7.1 You have a font that supports a character you need, but FieldWorks does not know about it................................................................................................................. 10 7.2 Unicode defines a new character you