Case Study: Least-Squares Solutions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
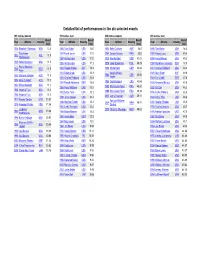
Detailed List of Performances in the Six Selected Events
Detailed list of performances in the six selected events 100 metres women 100 metres men 400 metres women 400 metres men Result Result Result Result Year Athlete Country Year Athlete Country Year Athlete Country Year Athlete Country (sec) (sec) (sec) (sec) 1928 Elizabeth Robinson USA 12.2 1896 Tom Burke USA 12.0 1964 Betty Cuthbert AUS 52.0 1896 Tom Burke USA 54.2 Stanislawa 1900 Frank Jarvis USA 11.0 1968 Colette Besson FRA 52.0 1900 Maxey Long USA 49.4 1932 POL 11.9 Walasiewicz 1904 Archie Hahn USA 11.0 1972 Monika Zehrt GDR 51.08 1904 Harry Hillman USA 49.2 1936 Helen Stephens USA 11.5 1906 Archie Hahn USA 11.2 1976 Irena Szewinska POL 49.29 1908 Wyndham Halswelle GBR 50.0 Fanny Blankers- 1908 Reggie Walker SAF 10.8 1980 Marita Koch GDR 48.88 1912 Charles Reidpath USA 48.2 1948 NED 11.9 Koen 1912 Ralph Craig USA 10.8 Valerie Brisco- 1920 Bevil Rudd SAF 49.6 1984 USA 48.83 1952 Marjorie Jackson AUS 11.5 Hooks 1920 Charles Paddock USA 10.8 1924 Eric Liddell GBR 47.6 1956 Betty Cuthbert AUS 11.5 1988 Olga Bryzgina URS 48.65 1924 Harold Abrahams GBR 10.6 1928 Raymond Barbuti USA 47.8 1960 Wilma Rudolph USA 11.0 1992 Marie-José Pérec FRA 48.83 1928 Percy Williams CAN 10.8 1932 Bill Carr USA 46.2 1964 Wyomia Tyus USA 11.4 1996 Marie-José Pérec FRA 48.25 1932 Eddie Tolan USA 10.3 1936 Archie Williams USA 46.5 1968 Wyomia Tyus USA 11.0 2000 Cathy Freeman AUS 49.11 1936 Jesse Owens USA 10.3 1948 Arthur Wint JAM 46.2 1972 Renate Stecher GDR 11.07 Tonique Williams- 1948 Harrison Dillard USA 10.3 1952 George Rhoden JAM 45.9 2004 BAH 49.41 1976 -

Pan-American Games, Caracas 1983
PAN-AMERICAN GAMES Caracas, Venezuela 1983 100 METRES (23 Aug) HEAT 1 (-2.60m) 1 Ben Johnson Canada 10.49 2 Sam Graddy USA 10.50 3 Raymond Stewart Jamaica 10.55 4 Wilfredo Almonte Dominican Republic 10.68 5 Luis Schneider Zuanich Chile 11.01 6 Katsuhiko Nakaia Brazil 12.93 Lester Benjamin Antigua and Barbuda DNRun HEAT 2 (-2.45m) 1 Leandro Peñalver Gonzalez Cuba 10.41 2 Juan Nuñez Lima Dominican Republic 10.51dq 3 Nelson Rocha dos Santos Brazil 10.62 4 Hipolito Timothy Brown Venezuela 10.68 5 Everard Samuels Jamaica 10.71 6 Calvin Greenaway Antigua and Barbuda 11.14 HEAT 3 (-2.52m) 1 Osvaldo Lara Canizares Cuba 10.41 2 Desai Williams Canada 10.58 3 Chris Brathwaite Trinidad and Tobago 10.58 4 Ken Robinson USA 10.69 5 Neville Hodge Gomez Virgin Islands 10.73 6 Florencio Aguilar Mejia Panama 10.81 7 Angel Andrade Venezuela 10.90 100 METRES (23 Aug) SEMI-FINALS HEAT 1 (-1.55m) 1 Leandro Peñalver Gonzalez Cuba 10.16 2 Sam Graddy USA 10.30 3 Raymond Stewart Jamaica 10.31 4 Desai Williams Canada 10.34 5 Nelson Rocha dos Santos Brazil 10.43 6 Wilfredo Almonte Dominican Republic 10.57 7 Neville Hodge Gomez Virgin Islands 10.73 8 Florencio Aguilar Mejia Panama 10.74 HEAT 2 (-1.44m) 1 Ben Johnson Canada 10.32 2 Osvaldo Lara Canizares Cuba 10.35 3 Juan Nuñez Lima Dominican Republic 10.52dq 4 Chris Brathwaite Trinidad and Tobago 10.53 5 Everard Samuels Jamaica 10.53 6 Ken Robinson USA 10.62 7 Hipolito Timothy Brown Venezuela 10.65 8 Luis Schneider Zuanich Chile 10.75 100 METRES (24 Aug) FINAL 1 Leandro Peñalver Gonzalez Cuba 10.06 2 Sam Graddy USA -

Cuban Tourism in 1997 Rose by 16.5 Percent
ISSN 1073-7715 www.cubanews.com Volume 6 Number 4 THE MIAMI HERALD PUBLISHING COMPANY April 1998 Editor’s Note MAJOR DEVELOPMENTS Clinton Policy Changes Oil Spill, Close Call When the U.S. Department of Defense transferred military responsibility for the The Clinton Administration eased U.S. pol- The collision of two small oil tankers in Caribbean from the Atlantic Command at icy toward Cuba by allowing the resumption Matanzas Bay resulted in a 6,700-barrel oil Norfolk, Va., to the Southern Command, of chartered flights and cash remittances spill that required a small army of workers and then moved SouthCom’s headquar- from the United States. More important, to clean up. Fortunately, the damage did not ters from Panama to Miami, many won- perhaps, Administration officials signaled a extend to nearby Varadero Beach. See Environment, Page 2 dered if SouthCom would be able to willingness to work with legislators to craft a maintain its independence so near to the bill that might loosen the embargo. See Washington Report, Page 2 Fishing Comeback vortex of anti-Castro politics. The moribund fishing industry is making We now have the answer and the Japanese Debt Deal answer is that moving to Miami has not a comeback after suffering a precipitous affected the military’s view of Cuba. That Perhaps even more important than the decline. The government says the export of is important news for those who wonder policy change, Cuba scored a breakthrough seafood has become one of the principal about influences on the debate over U.S. of sorts by renegotiating its $769 million sources of export earnings. -

Nacac Newsleter June 2016
NACAC NEWSLETTER JUNE 2016 Volume 3 Edition 1 NACAC NEWSLETER JUNE 2016 President Message 2 General Secretary 5 NACAC AA Executive Council 8 Resolution Women Commission Report 9 CADICA Cross Country 13 Championships NACAC Cross Country 15 Championships CARIFTA Games 17 Athletes of the OECS Diaspora 22 NACAC U23 El Salvador 2016 29 Visit to Cuba 30 Sponsors 36 1 NACAC NEWSLETTER JUNE 2016 Volume 3 Edition 1 PRESIDENT MESSAGE by Víctor López Therefore, as I expressed in many occasions to President Coe, to the Media and to colleagues and friends, it looks to me that we will have one of the best, if not the best year ever, as far as performances is concerned. I am not talking about the NACAC athletes only but athletes from all over the world. In other words, we will own the show in Río de Janeiro, Brazil at the 2016 Olympic Games. But in spite of the above opinion, from my part, as how great the performances have been so far, we still have to be vigilante because, for sure, we still have a problem On behalf of the NACAC Executive Council with doping in our sport and in other sports. and the NACAC Athletics Family, I would like Yes, it is important that we clean the house to extend my greetings in our newsletter of and face the challenges that we are this important year, perhaps the most experiencing but, it is more important that important in the history of our sport. There we continue to do what we do best, which is is no doubt that we are facing tough to develop our great sport and our young challenges and scandals never experienced people all over the world and at the same in the past. -

Men's 100M Diamond Discipline 12.05.2018
Men's 100m Diamond Discipline 12.05.2018 Start list 100m Time: 20:53 Records Lane Athlete Nat NR PB SB 1 Isiah YOUNG USA 9.69 9.97 10.02 WR 9.58 Usain BOLT JAM Berlin 16.08.09 2 Andre DE GRASSE CAN 9.84 9.91 10.15 AR 9.91 Femi OGUNODE QAT Wuhan 04.06.15 AR 9.91 Femi OGUNODE QAT Gainesville 22.04.16 3 Justin GATLIN USA 9.69 9.74 10.05 NR 9.99 Bingtian SU CHN Eugene 30.05.15 4 Bingtian SU CHN 9.99 9.99 10.28 NR 9.99 Bingtian SU CHN Beijing 23.08.15 5 Chijindu UJAH GBR 9.87 9.96 10.08 WJR 9.97 Trayvon BROMELL USA Eugene 13.06.14 6 Ramil GULIYEV TUR 9.92 9.97 MR 9.69 Tyson GAY USA 20.09.09 7 Yoshihide KIRYU JPN 9.98 9.98 DLR 9.69 Yohan BLAKE JAM Lausanne 23.08.12 8 Zhenye XIE CHN 9.99 10.04 SB 9.97 Ronnie BAKER USA Torrance 21.04.18 9 Reece PRESCOD GBR 9.87 10.03 10.39 2018 World Outdoor list 9.97 +0.5 Ronnie BAKER USA Torrance 21.04.18 Medal Winners Shanghai previous 10.01 +0.8 Zharnel HUGHES GBR Kingston 24.02.18 10.02 +1.9 Isiah YOUNG USA Des Moines, IA 28.04.18 2017 - London IAAF World Ch. in Winners 10.03 +0.8 Akani SIMBINE RSA Gold Coast 09.04.18 Athletics 17 Bingtian SU (CHN) 10.09 10.03 +1.9 Michael RODGERS USA Des Moines, IA 28.04.18 1. -

Congress Elections
CONGRESS ELECTIONS RETURN TOCANDIDATE LIST> IAAF CONGRESS ELECTIONS | ABOUT THE CANDIDATE Council Elections LIST OF CANDIDATES * PRESIDENT (1 SEAT) Sebastian COE (M) (GBR) VICE PRESIDENTS (4 SEATS)** Ahmad AL KAMALI (M) (UAE) Nawaf BIN MOHAMMED AL SAUD (M) (KSA) Sylvia BARLAG (F) (NED) Sergey BUBKA (M) (UKR) Geoffrey GARDNER (M) (NFI) Abby HOFFMAN (F) (CAN) Alberto JUANTORENA (M) (CUB) Ximena RESTREPO (F) (CHI) Ibrahim SHEHU-GUSAU (M) (NGR) Adille SUMARIWALLA (M) (IND) Jackson TUWEI (M) (KEN) INDIVIDUAL COUNCIL MEMBERS (13 SEATS)*** Andrey ABDUVALIEV (M) (UZB) Ahmad AL KAMALI (M) (UAE) Nawaf BIN MOHAMMED AL SAUD (M) (KSA) Sayar AL ANEZI (M) (KUW) Khaled AMARA (M) (TUN) Bernard AMSALEM (M) (FRA) Beatrice AYIKORU (F) (UGA) Willie BANKS (M) (USA) Sylvia BARLAG (F) (NED) Warren BLAKE (M) (JAM) Raul CHAPADO (M) (ESP) Nawal EL MOUTAWAKEL (F) (MAR) Sarifa FAGILDE (F) (MOZ) Evelyn FARRELL (F) (ARU) Walentina FEDJUSCHINA (F) (AUT) Abby HOFFMAN (F) (CAN) IAAF CONGRESS ELECTIONS | ABOUT THE CANDIDATE Alain JEAN-PIERRE (M) (HAI) Alberto JUANTORENA (M) (CUB) Dobromir KARAMARINOV (M) (BUL) Juergen KESSING (M) (GER) Dieudonne KWIZERA (M) (BDI) Bader Naser MOHAMED (M) (BRN) Elias MPONDELA (M) (ZAM) Claudia PEREZ OLMOS (F) (MEX) Antti PIHLAKOSKI (M) (FIN) Annette PURVIS (F) (NZL) Donna RAYNOR (F) (BER) Ximena RESTREPO (F) (CHI) Anna RICCARDI (F) (ITA) Ronald RUSSELL (M) (ISV) Muhammad Akram SAHI (M) (PAK) Ashkat SEISEMBEKOV (M) (KAZ) Aleck Thandisenzo SKHOSANA (M) (RSA) Edith SKIPPINGS (F) (TKS) Adille SUMARIWALLA (M) (IND) Siti TAWANG (F) (BRU) Jackson TUWEI (M) (KEN) Nan WANG (F) (CHN) Hiroshi YOKOKAWA (M) (JPN) Notes: * This list may be modified in case a person becomes not eligible or is otherwise found in breach of the Integrity Code of Conduct. -

Aproximaç˜Ao Polinomial
PSI-3260 Aplica¸c˜oes de Algebra´ Linear Experiˆencia 11 M´etodo dos M´ınimos Quadrados com SVD – Exerc´ıcio Desafio Parte 1 - Aproxima¸c˜ao polinomial Em um exerc´ıcio da Experiˆencia 8, usamos o m´etodo dos m´ınimos quadrados para obter o polinˆomio de grau m que melhor se ajusta a um conjunto de dados. Por conveniˆencia esse exerc´ıcio ´erepetido a seguir: 1. A Tabela 1 cont´em dados dos medalhistas de ouro da prova masculina de atletismo na modalidade de 400 metros rasos dos dez ´ultimos jogos ol´ımpicos (de 1972 a 2012). Utilizando os dados dessa tabela, pede-se: - As aproxima¸c˜oes polinomiais para o tempo da prova em fun¸c˜ao do ano. Considere aproxima¸c˜oes de primeira (reta), segunda (par´abola) e terceira ordens. Em um mesmo gr´afico, plote os dados e as aproxima¸c˜oes. Apresente tamb´em um gr´afico dos erros e compare as normas dos vetores de erro de cada aproxima¸c˜ao. Obs: Vocˆen˜ao precisa digitar os dados. Eles est˜ao no arquivo 400metros.mat dispon´ıvel no Moodle. - Para cada aproxima¸c˜ao, estime o tempo que se espera para essa prova nos jogos ol´ımpicos que ser˜ao realizados no Rio em 2016 e tamb´em nos jogos de 2028. Os tempos previstos pelas trˆes aproxima¸c˜oes s˜ao coerentes? Comente com base nos dados da Tabela 1. Tabela 1: Medalhistas de ouro da prova masculina atletismo na modalidade de 400 metros rasos dos dez ´ultimos jogos ol´ımpicos. Fonte: http://www.olympic.org/ Ano Local Medalhista de ouro Pa´ıs Tempo (s) 1972 Munique Vicent Matthews EUA 44.66 1976 Montreal Alberto Juantorena Cuba 44.26 1980 Moscou Viktor Martin URSS 44.60 1984 Los Angeles Alonzo Babers EUA 44.27 1988 Seul Steve Lewis EUA 43.87 1992 Barcelona Quincy Watts EUA 43.50 1996 Atlanta Michael Johnson EUA 43.49 2000 Sydney Michael Johnson EUA 43.84 2004 Atenas Jeremy Wariner EUA 44.00 2008 Pequim LaShawn Merritt EUA 43.75 2012 Londres Kirani James Granada 43.94 1 2 2. -

45Th CARIFTA GAMES 2016 Th Th 26 – 28 March
th 45 CARIFTA GAMES 2016 th th 26 – 28 March TECHNICAL MANUAL 45th CARIFTA GAMES NATIONAL ATHLETIC STADIUM, QUEENS PARK, ST. GEORGE’S, GRENADA MARCH 26th – 28th, 2016 1. LOCAL ORGANIZING COMMITTEE Chairperson Mrs. Veda Bruno Victor Deputy Chairman / Sponsorship Mr. Aaron Moses Secretary Ms. Jeanelle Gill Finance Ms. Claudia Francis Operations Mr. Conrad Francis Transportation Mr. Ralph James Volunteers Mr. John Williams Medical / Anti-Doping Dr. Sonia Phillip Ceremonies Mr. Thomas Matthew Legal Ms. Claudette Joseph Security Maj. Nigel Noel Media / Marketing Mr. Alvin Clouden Accommodation Mrs. Alison Felix-Burke Accreditation Mr. Don-Holman Phillip Protocol / Liaison Mrs. Elizabeth Greenidge 1 Advisor Mr. Charles George, President GAA Page 45th CARIFTA GAMES NATIONAL ATHLETIC STADIUM, QUEENS PARK, ST. GEORGE’S, GRENADA MARCH 26th – 28th, 2016 NACAC FAMILY President Mr. Victor Lopez PUR Vice President Mrs. Stephanie Hightower USA Treasurer Mr. Alain Jean-Pierre HAI General Secretary Mr. Michael Serralta TBC PUR Council Member Mrs. Geen Clarke CRC Council Member Mr. Alan Baboolal TTO Council Member Mr. Garth Gayle JAM Member Ex-Officio Lord Sebastian Coe GBR Member Ex-Officio Ms. Pauline Davis-Thompson BAH Member Ex-Officio Mr. Alberto Juantorena CUB Member Ex-Officio Ms. Abby Hoffman CAN Special Assistant to the President Mrs. Evelyn Lopez PUR MEET DELEGATES Organisational Delegate Mr. Keith Joseph SVG Technical Delegate Mr. Garth Gayle JAM Anti-Doping/Medical Delegate Dr. Adrian Lorde BAR INTERNATIONAL OFFICIALS International Technical Official Mr. John Andalcio TRI International Area Starter Mr. Patrick Harrigan IVB INTERNATIONAL AREA TECHNICAL OFFICIALS Mr. John Paul Clarke CAY Mr. Patrick Mathurin LCA 2 Mr. -

Men's 100M Diamond Race - Heat 1 22.07.2016
Men's 100m Diamond Race - Heat 1 22.07.2016 Start list 100m Time: 20:15 Records Lane Athlete Nat NR PB SB 1 Michael FRATER JAM 9.58 9.88 10.04 WR 9.58 Usain BOLT JAM Berlin 16.08.09 2 Chijindu UJAH GBR 9.87 9.96 10.06 AR 9.86 Francis OBIKWELU POR Athina 22.08.04 AR 9.86 Jimmy VICAUT FRA Paris 04.07.15 3 Michael RODGERS USA 9.69 9.85 9.97 AR 9.86 Jimmy VICAUT FRA Montreuil-sous-Bois 07.06.16 4 Marvin BRACY USA 9.69 9.93 9.94 NR 9.87 Linford CHRISTIE GBR Stuttgart 15.08.93 5 James DASAOLU GBR 9.87 9.91 10.11 WJR 9.97 Trayvon BROMELL USA Eugene 13.06.14 6 Aaron BROWN CAN 9.84 9.96 9.96 MR 9.78 Tyson GAY USA 13.08.10 7 Isiah YOUNG USA 9.69 9.99 10.03 DLR 9.69 Yohan BLAKE JAM Lausanne 23.08.12 8 Solomon BOCKARIE NED 9.91 10.13 10.13 SB 9.80 Justin GATLIN USA Eugene 03.07.16 9 Ojie EDOBURUN GBR 9.87 10.16 10.19 2016 World Outdoor list 9.80 +1.6 Justin GATLIN USA Eugene 03.07.16 Medal Winners Diamond Race 9.84 +1.6 Trayvon BROMELL USA Eugene 03.07.16 1 Justin GATLIN (USA) 20 9.86 +1.8 Jimmy VICAUT FRA Montreuil-sous-Bois 07.06.16 2016 - Amsterdam European Ch. 2 Michael RODGERS (USA) 13 9.88 +1.0 Usain BOLT JAM Kingston 11.06.16 1. -
Exploring Systems of Inequalities
ALGEBRA Explori g Systems of I equalities GAIL F. BURRILL AND PATRICK W. HOPFENSPERGER DATA-DRIVEN MATHEMATICS D A L E 5 E Y M 0 U R P U B L I C A T I 0 N S® Exploring Systems of Equations and Inequalities DATA-DRIVEN MATHEMATICS Gail F. Burrill and Patrick W. Hopfensperger Dale Seymour Pullllcatlons® White Plains, New York This material was produced as a part of the American Statistical Managing Editors: Catherine Anderson, Alan MacDonell Association's Project "A Data-Driven Curriculum Strand for Editorial Manager: John Nelson High School" with funding through the National Science Foundation, Grant #MDR-9054648. Any opinions, findings, Senior Mathematics Editor: Nancy R. Anderson conclusions, or recommendations expressed in this publication Consulting Editor: Maureen Laude are those of the authors and do not necessarily reflect the views of the National Science Foundation. Production/Manufacturing Director: Janet Yearian Production/Manufacturing Manager: Karen Edmonds Production Coordinator: Roxanne Knoll Design Manager: Jeff Kelly Cover and Text Design: Christy Butterfield Cover Photo: John Kelly, Image Bank This book is published by Dale Seymour Publications®, an Photo on page 3: AP/Wide World Photos imprint of Addison Wesley Longman, Inc. Dale Seymour Publications 10 Bank Street White Plains, NY 10602 Customer Service: 800-872-1100 Copyright © 1999 by Addison Wesley Longman, Inc. All rights reserved. No part of this publication may be reproduced in any form or by any means without the prior written permission of the publisher. Printed in the United States of America. Order number DS21845 ISBN 1-57232-539-9 1 2 3 4 5 6 7 8 9 10-ML-03 02 01 00 99 98 This Book Is Printed On Recycled Paper DALE SEYMOUR PUBLICATIONS® Aulllors GaU F. -
Case Study: Least-Squares Solutions
Case Study: Least-Squares Solutions In this case study, large systems of equations which have no solution are considered. The problem of readjusting the North American Datum is one such large system of equations; unfortunately, it is far too large a system to deal with, so instead the general method for solving these systems will be discussed: the method of least squares. The method of least squares is used when there is a system of equations Ax = b which has no solution. In such a case, a “solution” will be sought xˆ which makes the difference between Axˆ and b as small as possible. This “solution” is called a least-squares solution to the system Ax = b. As is shown in Section 6.5, the least-squares solution xˆ must satisfy the normal equations ATAxˆ = AT b Furthermore, if the columns of A are linearly independent, then ATA is invertible, and there is a unique least-squares solution xˆ =(ATA)−1AT b As described in Section 6.6, one way in which least-squares solutions are useful is in the fitting of a curve to a set of data. First rewrite the system as Xβ = y,whereX is called the design matrix, β is called the parameter vector,andy is called the observation vector. Then the least-squares solution to this system is βˆ =(XTX)−1XT y A least-squares solution may be used to see a trend in data and to use that trend to make predictions. Example 1: The following table lists the gold medalist in the men’s 400 meter run for each of last 7 Olympics along with the time of the race in seconds: Year Name Nation Time 1972 Vincent Matthews United States 44.66 1976 Alberto Juantorena Cuba 44.26 1980 Viktor Martin USSR 44.60 1984 Alonzo Babers United States 44.27 1988 Steven Lewis United States 43.87 1992 Quincy Watts United States 43.50 1996 Michael Johnson United States 43.49 2000 Michael Johnson United States 43.84 One might to attempt to predict the results of this race at the 2004 Olympics by fitting an appropri- ate curve through the data points above. -

World Rankings — Men's
World Rankings — Men’s 800 1947 © JIRO MOCHIZUKI/PHOTO RUN 1 .................. Doug Harris (New Zealand) 2 ................................... John Fulton (US) 3 ......... Niels Holst-Sörensen (Denmark) 4 ...........................Arthur Wint (Jamaica) 5 .................................... Bill Clifford (US) 6 ............................Reggie Pearman (US) 7 ................................. Mal Whitfield (US) 8 ......................Olle Ljunggren (Sweden) 9 .................Ingvar Bengtsson (Sweden) 10 .................... Hans Liljekvist (Sweden) 1948 1 ................................. Mal Whitfield (US) 2 ................... Marcel Hansenne (France) 3 ...........................Arthur Wint (Jamaica) 4 .................Ingvar Bengtsson (Sweden) 5 ................................... Herb Barten (US) 6 ...................... Hans Liljekvist (Sweden) 7 ......... Niels Holst-Sörensen (Denmark) 8 ............. Herluf Christensen (Denmark) 9 .............................. Bob Chambers (US) 10 .............................Tarver Perkins (US) 1949 1 ................................. Mal Whitfield (US) 2 ...........................Arthur Wint (Jamaica) 3 ................................... Herb Barten (US) 4 .............................Olle Åberg (Sweden) 5 .................Ingvar Bengtsson (Sweden) 6 ........ Heinz Ulzheimer (West Germany) 7 ................... Marcel Hansenne (France) 8 ..............................Don Gehrmann (US) 9 .................................... Pat Bowers (US) WR holder David 10 ...................... Stig