Aproximaç˜Ao Polinomial
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Arkansas Men's Track & Field Media Guide, 2012
University of Arkansas, Fayetteville ScholarWorks@UARK Arkansas Men's Track and Field Athletics 2012 Arkansas Men's Track & Field Media Guide, 2012 University of Arkansas, Fayetteville. Athletics Media Relations Follow this and additional works at: https://scholarworks.uark.edu/track-field-men Citation University of Arkansas, Fayetteville. Athletics Media Relations. (2012). Arkansas Men's Track & Field Media Guide, 2012. Arkansas Men's Track and Field. Retrieved from https://scholarworks.uark.edu/track- field-men/4 This Periodical is brought to you for free and open access by the Athletics at ScholarWorks@UARK. It has been accepted for inclusion in Arkansas Men's Track and Field by an authorized administrator of ScholarWorks@UARK. For more information, please contact [email protected]. TABLE OF CONTENTS 2011 SEC OUTDOOR CHAMPIONS Index 1-4 History and Records 49-84 Table of Contents 1 Razorback Olympians 50-51 Media Information 2 Cross Country Results and Records 52-54 Team Quick Facts 3 Indoor Results and Records 55-61 The Southeastern Conference 4 Outdoor Results and Records 62-70 Razorback All-Americans 71-75 2011 Review 5-10 Randal Tyson Track Center 76 2011 Indoor Notes 6-7 John McDonnell Field 77 2011 Outdoor Notes 8-9 Facility Records 78 2011 Top Times and Honors 10 John McDonnell 79 Two-Sport Student Athletes 80 2012 Preview 11-14 Razorback All-Time Lettermen 81-84 2012 Outlook 12-13 2012 Roster 14 The Razorbacks 15-40 Returners 16-35 Credits Newcomers 36-40 The 2012 University of Arkansas Razorback men’s track and fi eld media guide was designed by assistant The Staff 41-48 media relations director Zach Lawson with writting Chris Bucknam 42-43 assistance from Molly O’Mara and Chelcey Lowery. -

All Time Men's World Ranking Leader
All Time Men’s World Ranking Leader EVER WONDER WHO the overall best performers have been in our authoritative World Rankings for men, which began with the 1947 season? Stats Editor Jim Rorick has pulled together all kinds of numbers for you, scoring the annual Top 10s on a 10-9-8-7-6-5-4-3-2-1 basis. First, in a by-event compilation, you’ll find the leaders in the categories of Most Points, Most Rankings, Most No. 1s and The Top U.S. Scorers (in the World Rankings, not the U.S. Rankings). Following that are the stats on an all-events basis. All the data is as of the end of the 2019 season, including a significant number of recastings based on the many retests that were carried out on old samples and resulted in doping positives. (as of April 13, 2020) Event-By-Event Tabulations 100 METERS Most Points 1. Carl Lewis 123; 2. Asafa Powell 98; 3. Linford Christie 93; 4. Justin Gatlin 90; 5. Usain Bolt 85; 6. Maurice Greene 69; 7. Dennis Mitchell 65; 8. Frank Fredericks 61; 9. Calvin Smith 58; 10. Valeriy Borzov 57. Most Rankings 1. Lewis 16; 2. Powell 13; 3. Christie 12; 4. tie, Fredericks, Gatlin, Mitchell & Smith 10. Consecutive—Lewis 15. Most No. 1s 1. Lewis 6; 2. tie, Bolt & Greene 5; 4. Gatlin 4; 5. tie, Bob Hayes & Bobby Morrow 3. Consecutive—Greene & Lewis 5. 200 METERS Most Points 1. Frank Fredericks 105; 2. Usain Bolt 103; 3. Pietro Mennea 87; 4. Michael Johnson 81; 5. -

LIME Sponsors 100M and 400M World Athletic Champions
6 March 2012 LIME SPONSORS 100M and 400M WORLD ATHLETICS CHAMPIONS Cable & Wireless Communications’ Caribbean business, LIME, has agreed three-year sponsorship deals with two of the world’s fastest sprinters, Yohan Blake and Kirani James. The athletes will act as brand ambassadors for LIME throughout the Caribbean region. Yohan Blake, 22, is from Jamaica. He won the 100 metres sprint final at the 2011 World Athletics Championships. He also ran the fastest 200 metres time in 2011 - 19.26 seconds, which was the second fastest time in history. Yohan Blake said: "I am excited to have LIME as a partner and proud to be their brand ambassador as they are a great company that has contributed a lot to Jamaica's development. I am also very pleased with the level of support they have committed to my foundation, YB Afraid, which works to support young people in Jamaica. Both on and off the track, I intend to continue making LIME and all of Jamaica proud.” Kirani James, 19, is from Grenada and competes in 200 and 400 metres sprint events. Having won a host of championships at youth and college level, he burst into prominence as a senior in 2011 when he became the youngest ever 400 metres world champion at age 18. His victory in the 400 metres final at the 2011 World Athletics Championships in South Korea was the first medal for Grenada in any event at the Championships. Mr James described LIME as a, "prestigious, unique and loyal brand" and said he is looking forward to a great and fruitful partnership. -

Table of Contents
A Column By Len Johnson TABLE OF CONTENTS TOM KELLY................................................................................................5 A RELAY BIG SHOW ..................................................................................8 IS THIS THE COMMONWEALTH GAMES FINEST MOMENT? .................11 HALF A GLASS TO FILL ..........................................................................14 TOMMY A MAN FOR ALL SEASONS ........................................................17 NO LIGHTNING BOLT, JUST A WARM SURPRISE ................................. 20 A BEAUTIFUL SET OF NUMBERS ...........................................................23 CLASSIC DISTANCE CONTESTS FOR GLASGOW ...................................26 RISELEY FINALLY GETS HIS RECORD ...................................................29 TRIALS AND VERDICTS ..........................................................................32 KIRANI JAMES FIRST FOR GRENADA ....................................................35 DEEK STILL WEARS AN INDELIBLE STAMP ..........................................38 MICHAEL, ELOISE DO IT THEIR WAY .................................................... 40 20 SECONDS OF BOLT BEATS 20 MINUTES SUNSHINE ........................43 ROWE EQUAL TO DOUBELL, NOT DOUBELL’S EQUAL ..........................46 MOROCCO BOUND ..................................................................................49 ASBEL KIPROP ........................................................................................52 JENNY SIMPSON .....................................................................................55 -
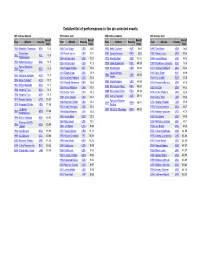
Detailed List of Performances in the Six Selected Events
Detailed list of performances in the six selected events 100 metres women 100 metres men 400 metres women 400 metres men Result Result Result Result Year Athlete Country Year Athlete Country Year Athlete Country Year Athlete Country (sec) (sec) (sec) (sec) 1928 Elizabeth Robinson USA 12.2 1896 Tom Burke USA 12.0 1964 Betty Cuthbert AUS 52.0 1896 Tom Burke USA 54.2 Stanislawa 1900 Frank Jarvis USA 11.0 1968 Colette Besson FRA 52.0 1900 Maxey Long USA 49.4 1932 POL 11.9 Walasiewicz 1904 Archie Hahn USA 11.0 1972 Monika Zehrt GDR 51.08 1904 Harry Hillman USA 49.2 1936 Helen Stephens USA 11.5 1906 Archie Hahn USA 11.2 1976 Irena Szewinska POL 49.29 1908 Wyndham Halswelle GBR 50.0 Fanny Blankers- 1908 Reggie Walker SAF 10.8 1980 Marita Koch GDR 48.88 1912 Charles Reidpath USA 48.2 1948 NED 11.9 Koen 1912 Ralph Craig USA 10.8 Valerie Brisco- 1920 Bevil Rudd SAF 49.6 1984 USA 48.83 1952 Marjorie Jackson AUS 11.5 Hooks 1920 Charles Paddock USA 10.8 1924 Eric Liddell GBR 47.6 1956 Betty Cuthbert AUS 11.5 1988 Olga Bryzgina URS 48.65 1924 Harold Abrahams GBR 10.6 1928 Raymond Barbuti USA 47.8 1960 Wilma Rudolph USA 11.0 1992 Marie-José Pérec FRA 48.83 1928 Percy Williams CAN 10.8 1932 Bill Carr USA 46.2 1964 Wyomia Tyus USA 11.4 1996 Marie-José Pérec FRA 48.25 1932 Eddie Tolan USA 10.3 1936 Archie Williams USA 46.5 1968 Wyomia Tyus USA 11.0 2000 Cathy Freeman AUS 49.11 1936 Jesse Owens USA 10.3 1948 Arthur Wint JAM 46.2 1972 Renate Stecher GDR 11.07 Tonique Williams- 1948 Harrison Dillard USA 10.3 1952 George Rhoden JAM 45.9 2004 BAH 49.41 1976 -
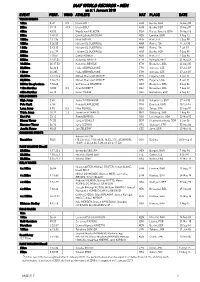
IAAF WORLD RECORDS - MEN As at 1 January 2018 EVENT PERF
IAAF WORLD RECORDS - MEN as at 1 January 2018 EVENT PERF. WIND ATHLETE NAT PLACE DATE TRACK EVENTS 100m 9.58 0.9 Usain BOLT JAM Berlin, GER 16 Aug 09 200m 19.19 -0.3 Usain BOLT JAM Berlin, GER 20 Aug 09 400m 43.03 Wayde van NIEKERK RSA Rio de Janeiro, BRA 14 Aug 16 800m 1:40.91 David Lekuta RUDISHA KEN London, GBR 9 Aug 12 1000m 2:11.96 Noah NGENY KEN Rieti, ITA 5 Sep 99 1500m 3:26.00 Hicham EL GUERROUJ MAR Roma, ITA 14 Jul 98 1 Mile 3:43.13 Hicham EL GUERROUJ MAR Roma, ITA 7 Jul 99 2000m 4:44.79 Hicham EL GUERROUJ MAR Berlin, GER 7 Sep 99 3000m 7:20.67 Daniel KOMEN KEN Rieti, ITA 1 Sep 96 5000m 12:37.35 Kenenisa BEKELE ETH Hengelo, NED 31 May 04 10,000m 26:17.53 Kenenisa BEKELE ETH Bruxelles, BEL 26 Aug 05 20,000m 56:26.0 Haile GEBRSELASSIE ETH Ostrava, CZE 27 Jun 07 1 Hour 21,285 Haile GEBRSELASSIE ETH Ostrava, CZE 27 Jun 07 25,000m 1:12:25.4 Moses Cheruiyot MOSOP KEN Eugene, USA 3 Jun 11 30,000m 1:26:47.4 Moses Cheruiyot MOSOP KEN Eugene, USA 3 Jun 11 3000m Steeplechase 7:53.63 Saif Saaeed SHAHEEN QAT Bruxelles, BEL 3 Sep 04 110m Hurdles 12.80 0.3 Aries MERRITT USA Bruxelles, BEL 7 Sep 12 400m Hurdles 46.78 Kevin YOUNG USA Barcelona, ESP 6 Aug 92 FIELD EVENTS High Jump 2.45 Javier SOTOMAYOR CUB Salamanca, ESP 27 Jul 93 Pole Vault 6.16i Renaud LAVILLENIE FRA Donetsk, UKR 15 Feb 14 Long Jump 8.95 0.3 Mike POWELL USA Tokyo, JPN 30 Aug 91 Triple Jump 18.29 1.3 Jonathan EDWARDS GBR Göteborg, SWE 7 Aug 95 Shot Put 23.12 Randy BARNES USA Los Angeles, USA 20 May 90 Discus Throw 74.08 Jürgen SCHULT GDR Neubrandenburg, GDR 6 Jun 86 Hammer Throw -

400M MEN All-Time List -- SPEED RESERVE Updated 10/14/19
200 to 400 relationship assume 400m is 2.223 x 200m 27.0 x 2.223 = 60.00 22.5 x 2.223 = 50.01 Setting training tempos special endurance intensive tempo Speed development defined = 95%+ of max speed Accel development defined = 95%+ of max intensity Setting training tempos (minimal) Start here, and progress from here 60.0 50.0 50-100m race pace to rp +1” 16.0 13.3 150-200m race pace to rp +2” 32.0 26.6 250-300m race pace to rp +3” 48.0 39.9 350-400m race pace to rp +4” 64.0 53.2 Helpful estimate: athletes will improve 2-3% every 2-3 weeks wk 1 5x 150 avg 24.0 (24.0 x .02 = .48) wk 2 wk 3 5x 150 avg 23.5 (23.5 x .02 = .47) wk 4 wk 5 5x 150 avg 23.1 ………………….. etc Helpful datum: Maximal effort for 5x 200m/ 5’ rest = athlete can average their 2nd 200m race tempo (or slightly better) Example: Clora Williams 51.07 51.07 x .524 = 26.7 5x 200 (3 assisted, 2 resisted) = 26.3 average in week 28-30 Progress template in a 38-42 week season: week 1-3 6-8x 150 at 85% intensive tempo week 4-6 6-8x 150 at 87% intensive tempo week 7 5x 200 at 85% intensive tempo / special endurance week 10 5x 200 at 87% week 15 5x 200 at 90% - Exams/Christmas follow week 18 5x 200 at 88% week 21 5x 200 at 91% week 23 5x 200 at 93% week 25 5x 200 at 95% week 27 5x 200 at 97% week 29 5x 200 at 99% - transition to 3-4x 200/ 6’ rest or short rest Example 1a start here! Wk 1-4 early season / general prep So: 5x 150 @ 85% / 4-5’ 32.0 x .75 = 24.0 26.6 x .75 = 20.0 60.0 50.0 200m 32.0 26.6 150m (.75) 24.0 20.0 Example 1b Wk 3-6 early season / general prep So: 5x 150 @ 87% / 4-5’ -

Pan-American Games, Caracas 1983
PAN-AMERICAN GAMES Caracas, Venezuela 1983 100 METRES (23 Aug) HEAT 1 (-2.60m) 1 Ben Johnson Canada 10.49 2 Sam Graddy USA 10.50 3 Raymond Stewart Jamaica 10.55 4 Wilfredo Almonte Dominican Republic 10.68 5 Luis Schneider Zuanich Chile 11.01 6 Katsuhiko Nakaia Brazil 12.93 Lester Benjamin Antigua and Barbuda DNRun HEAT 2 (-2.45m) 1 Leandro Peñalver Gonzalez Cuba 10.41 2 Juan Nuñez Lima Dominican Republic 10.51dq 3 Nelson Rocha dos Santos Brazil 10.62 4 Hipolito Timothy Brown Venezuela 10.68 5 Everard Samuels Jamaica 10.71 6 Calvin Greenaway Antigua and Barbuda 11.14 HEAT 3 (-2.52m) 1 Osvaldo Lara Canizares Cuba 10.41 2 Desai Williams Canada 10.58 3 Chris Brathwaite Trinidad and Tobago 10.58 4 Ken Robinson USA 10.69 5 Neville Hodge Gomez Virgin Islands 10.73 6 Florencio Aguilar Mejia Panama 10.81 7 Angel Andrade Venezuela 10.90 100 METRES (23 Aug) SEMI-FINALS HEAT 1 (-1.55m) 1 Leandro Peñalver Gonzalez Cuba 10.16 2 Sam Graddy USA 10.30 3 Raymond Stewart Jamaica 10.31 4 Desai Williams Canada 10.34 5 Nelson Rocha dos Santos Brazil 10.43 6 Wilfredo Almonte Dominican Republic 10.57 7 Neville Hodge Gomez Virgin Islands 10.73 8 Florencio Aguilar Mejia Panama 10.74 HEAT 2 (-1.44m) 1 Ben Johnson Canada 10.32 2 Osvaldo Lara Canizares Cuba 10.35 3 Juan Nuñez Lima Dominican Republic 10.52dq 4 Chris Brathwaite Trinidad and Tobago 10.53 5 Everard Samuels Jamaica 10.53 6 Ken Robinson USA 10.62 7 Hipolito Timothy Brown Venezuela 10.65 8 Luis Schneider Zuanich Chile 10.75 100 METRES (24 Aug) FINAL 1 Leandro Peñalver Gonzalez Cuba 10.06 2 Sam Graddy USA -

BRONZO 2016 Usain Bolt
OLIMPIADI L'Albo d'Oro delle Olimpiadi Atletica Leggera UOMINI 100 METRI ANNO ORO - ARGENTO - BRONZO 2016 Usain Bolt (JAM), Justin Gatlin (USA), Andre De Grasse (CAN) 2012 Usain Bolt (JAM), Yohan Blake (JAM), Justin Gatlin (USA) 2008 Usain Bolt (JAM), Richard Thompson (TRI), Walter Dix (USA) 2004 Justin Gatlin (USA), Francis Obikwelu (POR), Maurice Greene (USA) 2000 Maurice Greene (USA), Ato Boldon (TRI), Obadele Thompson (BAR) 1996 Donovan Bailey (CAN), Frank Fredericks (NAM), Ato Boldon (TRI) 1992 Linford Christie (GBR), Frank Fredericks (NAM), Dennis Mitchell (USA) 1988 Carl Lewis (USA), Linford Christie (GBR), Calvin Smith (USA) 1984 Carl Lewis (USA), Sam Graddy (USA), Ben Johnson (CAN) 1980 Allan Wells (GBR), Silvio Leonard (CUB), Petar Petrov (BUL) 1976 Hasely Crawford (TRI), Don Quarrie (JAM), Valery Borzov (URS) 1972 Valery Borzov (URS), Robert Taylor (USA), Lennox Miller (JAM) 1968 James Hines (USA), Lennox Miller (JAM), Charles Greene (USA) 1964 Bob Hayes (USA), Enrique Figuerola (CUB), Harry Jeromé (CAN) 1960 Armin Hary (GER), Dave Sime (USA), Peter Radford (GBR) 1956 Bobby-Joe Morrow (USA), Thane Baker (USA), Hector Hogan (AUS) 1952 Lindy Remigino (USA), Herb McKenley (JAM), Emmanuel McDonald Bailey (GBR) 1948 Harrison Dillard (USA), Norwood Ewell (USA), Lloyd LaBeach (PAN) 1936 Jesse Owens (USA), Ralph Metcalfe (USA), Martinus Osendarp (OLA) 1932 Eddie Tolan (USA), Ralph Metcalfe (USA), Arthur Jonath (GER) 1928 Percy Williams (CAN), Jack London (GBR), Georg Lammers (GER) 1924 Harold Abrahams (GBR), Jackson Scholz (USA), Arthur -

Passion on Display This Summer Five Media Profess- Ionals Were in Rio Reporting for Passion for Sport
UNIC Rio / Pedro Andrade SEPTEMBER 2016 EDITION Passion on Display This summer five media profess- ionals were in Rio reporting for Passion for Sport. One prayer request throughout their time was to gain access to athletes in order to interview them – a prayer request that was answered on a number of occasions. Passion for Sport reporter, Norman Brierley spoke to Michael Johnson (right) who you will recognise from his work with the BBC commentary team. Johnson had a distinguished career in track and field where he inset) taking the gold; Kirani James there’s a won four Olympic Gold medals and from Grenada the silver and the powerful eight World Championships and, USA’s LaShawn Meritt taking the God out until these Games, held the 400m bronze. More than that, van Niekerk there, world record for 17 years. He retired broke Johnson’s 400m world record, pushing us in 2000 and now, as well as working winning from the outside lane – the all to the as an athletics pundit, he has also first man to win from lane eight next level. developed a sports business and is since Eric Liddell in 1924. It’s just Getty Images for IAAF involved in charitable sports ventures. about us to leave “You know I have a passion for sport “a powerful God… it all in his hands and trust in him.” and one thing that is consistent pushing us to Silver medallist Kirani James is also amongst all three of those things… all a follower of Jesus Christ. Before of those organisations and all of the the next level.” the Games in Rio he competed at the things I’m involved with are related to IAAF Diamond League meeting in sport. -

Cuban Tourism in 1997 Rose by 16.5 Percent
ISSN 1073-7715 www.cubanews.com Volume 6 Number 4 THE MIAMI HERALD PUBLISHING COMPANY April 1998 Editor’s Note MAJOR DEVELOPMENTS Clinton Policy Changes Oil Spill, Close Call When the U.S. Department of Defense transferred military responsibility for the The Clinton Administration eased U.S. pol- The collision of two small oil tankers in Caribbean from the Atlantic Command at icy toward Cuba by allowing the resumption Matanzas Bay resulted in a 6,700-barrel oil Norfolk, Va., to the Southern Command, of chartered flights and cash remittances spill that required a small army of workers and then moved SouthCom’s headquar- from the United States. More important, to clean up. Fortunately, the damage did not ters from Panama to Miami, many won- perhaps, Administration officials signaled a extend to nearby Varadero Beach. See Environment, Page 2 dered if SouthCom would be able to willingness to work with legislators to craft a maintain its independence so near to the bill that might loosen the embargo. See Washington Report, Page 2 Fishing Comeback vortex of anti-Castro politics. The moribund fishing industry is making We now have the answer and the Japanese Debt Deal answer is that moving to Miami has not a comeback after suffering a precipitous affected the military’s view of Cuba. That Perhaps even more important than the decline. The government says the export of is important news for those who wonder policy change, Cuba scored a breakthrough seafood has become one of the principal about influences on the debate over U.S. of sorts by renegotiating its $769 million sources of export earnings. -

MEC Leeto Congratulates Wayde Van Niekerk on Olympic Gold
15 August 2016 MEC LEETO CONGRATULATES WAYDE VAN NIEKERK The Free State MEC for Sport, Arts, Culture and Recreation Mrs. NS Leeto would like to take this opportunity to congratulate Free State athlete Wayde van Niekerk on his magnificent achievement at the Rio 2016 Olympic Games. Van Niekerk became the first South African athlete to win an Olympic Gold medal at the Rio 2016 Olympic Games. In front of a boisterous Rio crowd, Van Niekerk broke the first track and field world record of these Games with a blistering 43.03 second run from the unlikely position of lane eight, destroying the two previous Olympic champions in the process. Michael Johnson’s world record of 43.18sec had stood since 1999 and rarely been seriously challenged. Van Niekerk did not impress in qualifying thus was drawn in lane eight, but when the gun went off he rocketed from the blocks. Initially he looked to run too fast through the first 200m, and the expectation was that Kirani James, the defending champion from Grenada, and LaShawn Merritt of the United States would haul Van Niekerk in through the bends. It didn’t happen. The South African in fact went faster in the second half of the race, sling-shooting into the home straight. His winning margin against one of the fastest 400m fields ever assembled is what makes this win even more special. It was, as Michael Johnson himself said on television commentary, “a massacre”. To crown it all, and as indicative of the magnitude of the moment, another legend of the track, Usain Bolt, made a special plea to go all the way into the stands after winning his own race to go and embrace Van Niekerk in congratulation.