Testing General Relativity with Low-Frequency, Space-Based Gravitational-Wave Detectors
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Cape Canaveral Air Force Station Support to Commercial Space Launch
The Space Congress® Proceedings 2019 (46th) Light the Fire Jun 4th, 3:30 PM Cape Canaveral Air Force Station Support to Commercial Space Launch Thomas Ste. Marie Vice Commander, 45th Space Wing Follow this and additional works at: https://commons.erau.edu/space-congress-proceedings Scholarly Commons Citation Ste. Marie, Thomas, "Cape Canaveral Air Force Station Support to Commercial Space Launch" (2019). The Space Congress® Proceedings. 31. https://commons.erau.edu/space-congress-proceedings/proceedings-2019-46th/presentations/31 This Event is brought to you for free and open access by the Conferences at Scholarly Commons. It has been accepted for inclusion in The Space Congress® Proceedings by an authorized administrator of Scholarly Commons. For more information, please contact [email protected]. Cape Canaveral Air Force Station Support to Commercial Space Launch Colonel Thomas Ste. Marie Vice Commander, 45th Space Wing CCAFS Launch Customers: 2013 Complex 41: ULA Atlas V (CST-100) Complex 40: SpaceX Falcon 9 Complex 37: ULA Delta IV; Delta IV Heavy Complex 46: Space Florida, Navy* Skid Strip: NGIS Pegasus Atlantic Ocean: Navy Trident II* Black text – current programs; Blue text – in work; * – sub-orbital CCAFS Launch Customers: 2013 Complex 39B: NASA SLS Complex 41: ULA Atlas V (CST-100) Complex 40: SpaceX Falcon 9 Complex 37: ULA Delta IV; Delta IV Heavy NASA Space Launch System Launch Complex 39B February 4, 2013 Complex 46: Space Florida, Navy* Skid Strip: NGIS Pegasus Atlantic Ocean: Navy Trident II* Black text – current programs; -

Black Hole Termodinamics and Hawking Radiation
Black hole thermodynamics and Hawking radiation (Just an overview by a non-expert on the field!) Renato Fonseca - 26 March 2018 – for the Journal Club Thermodynamics meets GR • Research in the 70’s convincingly brought together two very different areas of physics: thermodynamics and General Relativity • People realized that black holes (BHs) followed some laws similar to the ones observed in thermodynamics • It was then possible to associate a temperature to BHs. But was this just a coincidence? • No. Hawkings (1975) showed using QFT in curved space that BHs from gravitational collapse radiate as a black body with a certain temperature T Black Holes Schwarzschild metric (for BHs with no spin nor electric charge) • All coordinates (t,r,theta,phi) are what you think they are far from the central mass M • Something funny seems to happen for r=2M. But … locally there is nothing special there (only at r=0): r=0: real/intrinsic singularity r=2M: apparent singularity (can be removed with other coordinates) Important caveat: the Schwarzschild solution is NOT what is called maximal. With coordinates change we can get the Kruskal solution, which is. “Maximal”= ability to continue geodesics until infinity or an intrinsic singularity Schwarzschild metric (for BHs with no spin nor electric charge) • r=2M (event horizon) is not special for its LOCAL properties (curvature, etc) but rather for its GLOBAL properties: r<=2M are closed trapped surfaces which cannot communicate with the outside world [dr/dt=0 at r=2M even for light] Fun fact: for null geodesics (=light) we see that +/- = light going out/in One can even integrate this: t=infinite for even light to fall into the BH! This is what an observatory at infinity sees … (Penrose, 1969) Schwarzschild metric (digression) • But the object itself does fall into the BH. -

Hawking Radiation As Perceived by Different Observers L C Barbado, C Barceló, L J Garay
Hawking radiation as perceived by different observers L C Barbado, C Barceló, L J Garay To cite this version: L C Barbado, C Barceló, L J Garay. Hawking radiation as perceived by different observers. Classical and Quantum Gravity, IOP Publishing, 2011, 10 (12), pp.125021. 10.1088/0264-9381/28/12/125021. hal-00710459 HAL Id: hal-00710459 https://hal.archives-ouvertes.fr/hal-00710459 Submitted on 21 Jun 2012 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Confidential: not for distribution. Submitted to IOP Publishing for peer review 24 March 2011 Hawking radiation as perceived by different observers LCBarbado1,CBarcel´o1 and L J Garay2,3 1 Instituto de Astrof´ısica de Andaluc´ıa(CSIC),GlorietadelaAstronom´ıa, 18008 Granada, Spain 2 Departamento de F´ısica Te´orica II, Universidad Complutense de Madrid, 28040 Madrid, Spain 3 Instituto de Estructura de la Materia (CSIC), Serrano 121, 28006 Madrid, Spain E-mail: [email protected], [email protected], [email protected] Abstract. We use a method recently introduced in Barcel´o et al, 10.1103/Phys- RevD.83.041501, to analyse Hawking radiation in a Schwarzschild black hole as per- ceived by different observers in the system. -

Effect of Quantum Gravity on the Stability of Black Holes
S S symmetry Article Effect of Quantum Gravity on the Stability of Black Holes Riasat Ali 1 , Kazuharu Bamba 2,* and Syed Asif Ali Shah 1 1 Department of Mathematics, GC University Faisalabad Layyah Campus, Layyah 31200, Pakistan; [email protected] (R.A.); [email protected] (S.A.A.S.) 2 Division of Human Support System, Faculty of Symbiotic Systems Science, Fukushima University, Fukushima 960-1296, Japan * Correspondence: [email protected] Received: 10 April 2019; Accepted: 26 April 2019; Published: 5 May 2019 Abstract: We investigate the massive vector field equation with the WKB approximation. The tunneling mechanism of charged bosons from the gauged super-gravity black hole is observed. It is shown that the appropriate radiation consistent with black holes can be obtained in general under the condition that back reaction of the emitted charged particle with self-gravitational interaction is neglected. The computed temperatures are dependant on the geometry of black hole and quantum gravity. We also explore the corrections to the charged bosons by analyzing tunneling probability, the emission radiation by taking quantum gravity into consideration and the conservation of charge and energy. Furthermore, we study the quantum gravity effect on radiation and discuss the instability and stability of black hole. Keywords: higher dimension gauged super-gravity black hole; quantum gravity; quantum tunneling phenomenon; Hawking radiation 1. Introduction General relativity is associated with the thermodynamics and quantum effect which are strongly supportive of each other. A black hole (BH) is a compact object whose gravitational pull is so intense that can not escape the light. -
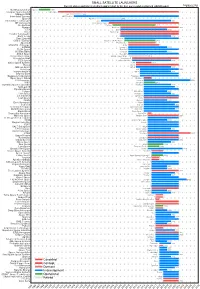
Small Satellite Launchers
SMALL SATELLITE LAUNCHERS NewSpace Index 2020/04/20 Current status and time from development start to the first successful or planned orbital launch NEWSPACE.IM Northrop Grumman Pegasus 1990 Scorpius Space Launch Demi-Sprite ? Makeyev OKB Shtil 1998 Interorbital Systems NEPTUNE N1 ? SpaceX Falcon 1e 2008 Interstellar Technologies Zero 2021 MT Aerospace MTA, WARR, Daneo ? Rocket Lab Electron 2017 Nammo North Star 2020 CTA VLM 2020 Acrux Montenegro ? Frontier Astronautics ? ? Earth to Sky ? 2021 Zero 2 Infinity Bloostar ? CASIC / ExPace Kuaizhou-1A (Fei Tian 1) 2017 SpaceLS Prometheus-1 ? MISHAAL Aerospace M-OV ? CONAE Tronador II 2020 TLON Space Aventura I ? Rocketcrafters Intrepid-1 2020 ARCA Space Haas 2CA ? Aerojet Rocketdyne SPARK / Super Strypi 2015 Generation Orbit GoLauncher 2 ? PLD Space Miura 5 (Arion 2) 2021 Swiss Space Systems SOAR 2018 Heliaq ALV-2 ? Gilmour Space Eris-S 2021 Roketsan UFS 2023 Independence-X DNLV 2021 Beyond Earth ? ? Bagaveev Corporation Bagaveev ? Open Space Orbital Neutrino I ? LIA Aerospace Procyon 2026 JAXA SS-520-4 2017 Swedish Space Corporation Rainbow 2021 SpinLaunch ? 2022 Pipeline2Space ? ? Perigee Blue Whale 2020 Link Space New Line 1 2021 Lin Industrial Taymyr-1A ? Leaf Space Primo ? Firefly 2020 Exos Aerospace Jaguar ? Cubecab Cab-3A 2022 Celestia Aerospace Space Arrow CM ? bluShift Aerospace Red Dwarf 2022 Black Arrow Black Arrow 2 ? Tranquility Aerospace Devon Two ? Masterra Space MINSAT-2000 2021 LEO Launcher & Logistics ? ? ISRO SSLV (PSLV Light) 2020 Wagner Industries Konshu ? VSAT ? ? VALT -

Space Coast Is Getting Busy: 6 New Rockets Coming to Cape Canaveral, KSC
4/16/2019 Space Coast is getting busy: 6 new rockets coming to Cape Canaveral, KSC Space Coast is getting busy: 6 new rockets coming to Cape Canaveral, Kennedy Space Center Emre Kelly, Florida Today Published 4:04 p.m. ET April 11, 2019 | Updated 7:53 a.m. ET April 12, 2019 COLORADO SPRINGS, Colo. – If schedules hold, the Space Coast will live up to its name over the next two years as a half-dozen new rockets target launches from sites peppered across the Eastern Range. Company, government and military officials here at the 35th Space Symposium, an annual space conference, have reaffirmed their plans to launch rockets ranging from more traditional heavy-lift behemoths to smaller vehicles that take advantage of new manufacturing technologies. Even if some of these schedules slip, at least one thing is apparent to several spaceflight experts here: The Eastern Range is seeing an unprecedented growth in commercial space companies and efforts. Space Launch System: 2020 NASA's Space Launch System rocket launches from Kennedy Space Center's pad 39B in this rendering by the agency. (Photo: NASA) NASA's long-awaited SLS, a multibillion-dollar rocket announced in 2011, is slated to become the most powerful launch vehicle in history if it can meet a stringent late 2020 deadline. The 322-foot-tall rocket is expected to launch on its first flight – Exploration Mission 1 – from Kennedy Space Center with an uncrewed Orion capsule for a mission around the moon, which fits in with the agency's wider goal of putting humans on the surface by 2024. -

Firewalls and the Quantum Properties of Black Holes
Firewalls and the Quantum Properties of Black Holes A thesis submitted in partial fulfillment of the requirements for the degree of Bachelor of Science degree in Physics from the College of William and Mary by Dylan Louis Veyrat Advisor: Marc Sher Senior Research Coordinator: Gina Hoatson Date: May 10, 2015 1 Abstract With the proposal of black hole complementarity as a solution to the information paradox resulting from the existence of black holes, a new problem has become apparent. Complementarity requires a vio- lation of monogamy of entanglement that can be avoided in one of two ways: a violation of Einstein’s equivalence principle, or a reworking of Quantum Field Theory [1]. The existence of a barrier of high-energy quanta - or “firewall” - at the event horizon is the first of these two resolutions, and this paper aims to discuss it, for Schwarzschild as well as Kerr and Reissner-Nordstr¨omblack holes, and to compare it to alternate proposals. 1 Introduction, Hawking Radiation While black holes continue to present problems for the physical theories of today, quite a few steps have been made in the direction of understanding the physics describing them, and, consequently, in the direction of a consistent theory of quantum gravity. Two of the most central concepts in the effort to understand black holes are the black hole information paradox and the existence of Hawking radiation [2]. Perhaps the most apparent result of black holes (which are a consequence of general relativity) that disagrees with quantum principles is the possibility of information loss. Since the only possible direction in which to pass through the event horizon is in, toward the singularity, it would seem that information 2 entering a black hole could never be retrieved. -
![Arxiv:1410.1486V2 [Gr-Qc] 26 Aug 2015](https://docslib.b-cdn.net/cover/3963/arxiv-1410-1486v2-gr-qc-26-aug-2015-893963.webp)
Arxiv:1410.1486V2 [Gr-Qc] 26 Aug 2015
October 2014 Black Hole Thermodynamics S. Carlip∗ Department of Physics University of California Davis, CA 95616 USA Abstract The discovery in the early 1970s that black holes radiate as black bodies has radically affected our understanding of general relativity, and offered us some early hints about the nature of quantum gravity. In this chapter I will review the discovery of black hole thermodynamics and summarize the many indepen- dent ways of obtaining the thermodynamic and (perhaps) statistical mechanical properties of black holes. I will then describe some of the remaining puzzles, including the nature of the quantum microstates, the problem of universality, and the information loss paradox. arXiv:1410.1486v2 [gr-qc] 26 Aug 2015 ∗email: [email protected] 1 Introduction The surprising discovery that black holes behave as thermodynamic objects has radically affected our understanding of general relativity and its relationship to quantum field theory. In the early 1970s, Bekenstein [1, 2] and Hawking [3, 4] showed that black holes radiate as black bodies, with characteristic temperatures and entropies ~κ Ahor kTH = ;SBH = ; (1.1) 2π 4~G where κ is the surface gravity and Ahor is the area of the horizon. These quantities appear to be inherently quantum gravitational, in the sense that they depend on both Planck's constant ~ and Newton's constant G. The resulting black body radiation, Hawking radiation, has not yet been directly observed: the temperature of an astrophysical black hole is on the order of a microkelvin, far lower than the cosmic microwave background temperature. But the Hawking temperature and the Bekenstein-Hawking entropy have been derived in so many independent ways, in different settings and with different assumptions, that it seems extraordinarily unlikely that they are not real. -

BLACK HOLE THERMODYNAMICS the Horizon Area Theorem 1970: Stephen Hawking Uses the Theory of General Relativity to Derive the So-Called
BLACK HOLE THERMODYNAMICS The horizon area theorem 1970: Stephen Hawking uses the theory of general relativity to derive the so-called Horizon area theorem The total horizon area in a closed system containing black holes never decreases. It can only increase or stay the same. [Stephen Hawking] Analogy between the area theorem and the 2nd law of thermodynamic Shortly after Stephen Hawking Formulated the area theorem, Jacob Beckenstein, at the time a graduate student at Princeton, noticed the analogy between the area theorem and the 2nd law of thermodynamics: [Jacob Beckenstein] The total area of a closed system never decreases. Entropy: logarithm of the number of ways you can relocate the atoms and molecules of a system without changing the overall properties of the system. Example of entropy: toys in a playroom (Thorne, pg. 424) Extremely orderly: 20 toys on 1 tile This playroom floor has 100 tiles, on which the kids can arrange 20 different toys. Parents prefer the toys to be kept in an extremely orderly configuration, with all the toys piled on one tile in one corner, as shown. There is only one such arrangement; the entropy of this configuration is thus the Number of equivalent rearrangements = 1; logarithm of 1, which is zero. entropy = 0. [This and next two slides courtesy of D. Watson] Entropy in a playroom (continued) Orderly: 20 toys on 10 tiles Parents might even accept this somewhat less orderly configuration: 20 different toys on 10 specific tiles. But there are lots of different equivalent arrangements (e.g. swapping the positions of two toys on different tiles produces a different arrangement that’s still acceptable): 1020 of them, in Number of equivalent rearrangements = 1020; fact, for an entropy value of “entropy” = 20. -

Espinsights the Global Space Activity Monitor
ESPInsights The Global Space Activity Monitor Issue 6 April-June 2020 CONTENTS FOCUS ..................................................................................................................... 6 The Crew Dragon mission to the ISS and the Commercial Crew Program ..................................... 6 SPACE POLICY AND PROGRAMMES .................................................................................... 7 EUROPE ................................................................................................................. 7 COVID-19 and the European space sector ....................................................................... 7 Space technologies for European defence ...................................................................... 7 ESA Earth Observation Missions ................................................................................... 8 Thales Alenia Space among HLS competitors ................................................................... 8 Advancements for the European Service Module ............................................................... 9 Airbus for the Martian Sample Fetch Rover ..................................................................... 9 New appointments in ESA, GSA and Eurospace ................................................................ 10 Italy introduces Platino, regions launch Mirror Copernicus .................................................. 10 DLR new research observatory .................................................................................. -

The Right Rocket for the Job: Small Launch Providers Target Small Satellites
The Right Rocket for the Job: Small Launch Providers Target Small Satellites An STS Research Paper presented to the faculty of the School of Engineering and Applied Science University of Virginia by Gabriel Norris May 11, 2020 On my honor as a University student, I have neither given nor received unauthorized aid on this assignment as defined by the Honor Guidelines for Thesis-Related Assignments. Signed: _________________________________________________ Approved: _______________________________________ Date ________________________ Peter Norton, Department of Engineering and Society 2 The University of Virginia Department of Mechanical and Aerospace Engineering has its first satellite, Libertas, now in orbit and plans to launch two more within the next three years. This sudden activity is representative of the vastly increased smallsat1 launch cadence by a variety of groups around the world. The trend is facilitated by the reduced cost and relative ease of assembly conferred by CubeSats, which collectively make up 70 percent of satellites launched today (Halt & Wieger, 2019). Startups, underdeveloped countries, and universities that, just ten years ago, would have been incapable of any kind of space mission are now launching several. From 2012 to 2019, 663 CubeSats were manufactured by private companies, nearly 300 by governments or militaries, and 371 by academic institutions. Yearly satellite launches have increased six-fold in this time (Halt & Wieger, 2019; fig. 1). This marked increase in customers underscores a sociotechnical problem in the rocketry industry: most rockets are fairly large and cater primarily to large satellites, leaving behind a large number of customers in the smallsat domain. Satellites broadly fall within four categories of use: remote sensing, communication, technology demonstration, and scientific investigation. -

Black Hole Thermodynamics
Black Hole Thermodynamics Reading: Wald 12.5 There is good evidence that after formation black holes relax to stationary configurations, characterized by mass, angular momentum, and gauge charges. This is a negligible amount of data compared to the many ways we can form black holes, suggesting that they ought to be thought of as thermodynamic entities. If so we need to identify their temperature and entropy and ask if they satisfy the laws of thermodynamics. This was a great discovery by Bekenstein and Hawking who showed black holes are thermal only after quantum effects are taken into account and their entropy is the horizon area=4G. To motivate these answers, let us return to the Kerr solution and consider the area of a constant t section of the horizon. The induced metric is (r2 + a2)2 ds2 = Σdθ2 + + sin2 θ d'2; (1) Σ and the resulting area is 2 2 2 2 p 4 4 2 2 A = 4π(r+ + a ) = 8π(G M + G M − G J ): (2) In the last step we used J = Ma and the definition of r+ to write A in terms of black hole mass and spin. Under an infinitesimal change dM and dJ, we obtaind p G4M 4 − G2J 2 dM = Ω dJ + dA: (3) H 2G2MA This equation is reminding of the first law of thermodynamics dE = µdQ + T dS (in a system with rotation symmetry, Ω is the chemical potential associated to the conserved charge J). It suggests identifying the horizon area with black hole entropy SBH / A; (4) though we need a different calculation to determine the temperature and hence the (positive) proportionality constant.