HW4 Part II Due: DP (2Pm)
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Doyle Bramhall
BIO DOYLE BRAMHALL It’s apropos that DOYLE BRAMHALL’s new Yep Roc CD is titled Is It News because, although they’re absolutely true to his deep roots in the blues, its dozen original tunes mark a turning point that is both ambitious and the logical summation of his artistic evolution. The answer to the forward- thinking, envelope-pushing CD’s title is a resounding yes—and the news is all good! “I wanted to make an all-original record that was big, energetic, intimate, and unpredictable,” Doyle states. “We got a lot of the sounds by pushing everything to the limit and then pulling it back from there.” Fans already accustomed to Doyle’s high standards and willingness to chart new territory will nonetheless be pleased and surprised at just how high he raises the bar. This instant classic is the benchmark of Bramhall’s storied career—which is saying a lot! Continuing the tradition he started with the songs he co-wrote with Stevie Ray Vaughan, which struck a chord with the biggest audience the blues has ever enjoyed, he deftly expands the idiom’s vocabulary and texture. Any discussion of Texas blues, be it T-Bone Walker or Stevie Ray, is incomplete without mention of Doyle Bramhall. As singer, songwriter, and drummer, he has been an integral part of that rich state’s music for almost 40 years and, indeed, one of the founding fathers of the blues/roots resurgence synonymous with the Lone Star state and the migration from Dallas to its musical epicenter, Austin. -

English Release Fernando Noronha 10-14
"I feel extremely happy and proud when I see such a young band playing the Blues so well." (B.B. King) release http://www.youtube.com/watch?v=A31U05Cp3_4&list=UUioje3HIhqE3jFMyMdMbqYQ&feature=share httttp:://www..youttube..com/wattch?v=A31U05Cp3_4&lliistt=UUiiojje3HIhqE3jjFMyMdMbqYQ&ffeatturre=sharre httttp:://www..youttube..com/wattch?v=A31U05Cp3_4&lliistt=UUiiojje3HIhqE3jjFMyMdMbqYQ&ffeatturre=sharre http://www.youtube.com/watch?v=A31U05Cp3_4&list=UUioje3HIhqE3jFMyMdMbqYQ&feature=share httttp:://www..youttube..com/wattch?v=A31U05Cp3_4&lliistt=UUiiojje3HIhqE3jjFMyMdMbqYQ&ffeatturre=sharre http://www.youtube.com/watch?v=A31U05Cp3_4&list=UUioje3HIhqE3jFMyMdMbqYQ&feature=share httttp:://www..youttube..com/wattch?v=A31U05Cp3_4&lliistt=UUiiojje3HIhqE3jjFMyMdMbqYQ&ffeatture=share http://www.youtube.com/watch?v=A31U05Cp3_4&list=UUioje3HIhqE3jFMyMdMbqYQ&feature=share httttp:://www..youttube..com/wattch?v=A31U05Cp3_4&lliistt=UUiiojje3HIIhqE3jjFMyMdMbqYQ&ffeatturre=sharre http://www.youtube.com/watch?v=A31U05Cp3_4&list=UUioje3HIhqE3jFMyMdMbqYQ&feature=share httttp:://www..youttube..com/wattch?v=A31U05Cp3_4&lliistt=UUiiojje3HIhqE3jjFMyMdMbqYQ&ffeatturre=sharre http://www.youtube.com/watch?v=A31U05Cp3_4&list=UUioje3HIhqE3jFMyMdMbqYQ&feature=share httttp:://www..youttube..com/wattch?v=A31U05Cp3_4&lliistt=UUiiojje3HIhqE3jjFMyMdMbqYQ&ffeatturre=sharre http://www.youtube.com/watch?v=A31U05Cp3_4&list=UUioje3HIhqE3jFMyMdMbqYQ&feature=share httttp:://www..youttube..com/wattch?v=A31U05Cp3_4&lliistt=UUiiojje3HIhqE3jjFMyMdMbqYQ&ffeatturre=sharre http://www.youtube.com/watch?v=A31U05Cp3_4&list=UUioje3HIhqE3jFMyMdMbqYQ&feature=share -

Dance Arts Society
4.0 and GO Tutorina Page 4 • The Battalion Assielife Friday • January 27, Located at 700 E. University Dr. Suite 108 Behind Golden Corral and Blockbuster Video across from the Hilton This Week/ Monday Tuesday Wednesday Thursday Friday Tribal Nation will be playing Ray Vaughan, but he said he reggae music at 3rd Floor has a more aggressive style. 01/30 01/31 02/01 02/02 Cantina's TAMU's Caribbean See related story, Page 3. Brave Combo, a band from Club party. The special event is Denton, TX will be playing at open to the public and will Jerk, a rock cover band/will|)i BANA 303 BANA 303 BANA 303 BANA 303 Stafford Opera House. A group of have Jamaican D.J.'s during the returning to The Tap. 5 -7 pm students from University of North Part 1 Part II Part III Part IV band's breaks. Texas, Brave Combo mixes rock The Maps, a rock and blues and Latin rhythms in their return band, will be playing at Swee! MATH 152 MATH 152 MATH 152 MATH 152 trip to Stafford. Saturday 7-9 pm Eugene's. Part 1 Part II Part III Part IV A* Mother's Monkey, an alternative Big Otis, a Motown and soul Moe Bandy, a veteran countn rock band, will be at Sweet singer, will be at 3rd Floor singer, will be at The Texas FINC 341 FINC 341 FINC 341 FINC 341 Eugene's. Cantina. 10-12 pm Hall of Fame. He performs Part 1 Part III Part IV throughout the year at his Part II Peeping Tom, a local cover band Chris Duarte, Texas blues American Theater in Bransom that plays some original songs, guitarist out of Austin, will be MO, but is taking his showon 4.0 amt Qo is Located OK; the, Centeypole^ Bus Routes! plays regularly at The Tap. -
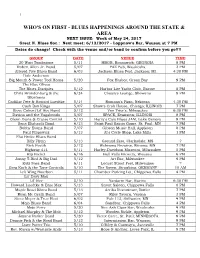
WHO's on FIRST - BLUES HAPPENINGS AROUND the STATE & AREA NEXT ISSUE: Week of May 24, 2017 Great N
1 WHO'S ON FIRST - BLUES HAPPENINGS AROUND THE STATE & AREA NEXT ISSUE: Week of May 24, 2017 Great N. Blues Soc.: Next meet: 6/13/2017 - Loppnow's Bar, Wausau at 7 PM Dates do change! Check with the venue and/or band to confirm before you go!!!! GROUP DATE VENUE TIME 20 Watt Tombstone 5/11 HBGB, Brunswick; GEORGIA 8 PM Robert Allen Jr. Band 5/07 PAZ Pub, Waukesha 3 PM Altered Five Blues Band 6/03 Jackson Blues Fest, Jackson; MI. 4:30 PM Dale Anderson Big Mouth & Power Tool Horns 5/20 Fox Harbor, Green Bay 9 PM The Blue Olives The Blues Disciples 5/12 Harbor Lite Yacht Club, Racine 8 PM Chris Brandenburg & the 6/24 Classics Lounge, Shawano 8 PM Bluetones Cadillac Pete & Howard Luedtke 5/14 Romano's Pizza, Nekoosa 4:30 PM Cash Box Kings 5/07 Shaw's Crab House, Chicago; ILLINOIS 7 PM Steve Cohen/Lil' Rev Band 5/12 Von Trier's, Milwaukee 6:30 PM Davina and the Vagabonds 5/07 SPACE, Evanston; ILLINOIS 8 PM Glenn Davis & Cruise Control 5/10 Harry's Cafe Blues JAM, Lake Geneva 9 PM Sena Ehrhardt Band 6/13 Saint Paul Saints Game, St. Paul; MN 7 PM Bobby Evans Band 7/07 Gibson Music Hall, Appleton 8 PM Paul Filipowicz 5/13 Al's Cycle Shop, Lake Mills 1 PM Flat Broke Blues Band Billy Flynn 5/13 Ground Zero, Clarksdale; MS ? Nick Foytik 5/12 Wehnona Brewing, Winona; MN 7 PM Highway 414 5/11 Harley-Davidson Museum, Milwaukee 5 PM Hip Pocket 6/16 Bull Falls Brewery, Wausau 6 PM Jonny T-Bird & Big Dad 5/12 Art Bar, Milwaukee 9 PM Katz Sass Band 6/11 Locust Street Fest, Milwaukee ? Greg Koch & the Tone Controls 5/10 The Raven, Straubing, GERMANY 10 -

Kcck.Org Telsen, Skeeter Louis and Dennis “Daddy-O” Dartanyan Brown Ron Dewitte Mcmurrin
JULY2013 Cool Issue 228 The Publication of the Linn County Blues Society - lcbs.org July 2013 scan for LCBS web info 52406-2672 Cedar Rapids, IA Rapids, Cedar PO Box 2672 Box PO Linn County Blues Society Blues County Linn also featuring Current list of members Scott Holt of the IBHOF Big Mike Edwards James Kinds Bluesmore20! Billylee Janey Jim DeKoster Bo Ramsey Jimmy Pryor Bob DeForest Joanne Jackson Bob Dorr Joe Price Bob Pace Louis McTizic LCBS ALL STARS! Bruce McCabe Mel Harper Ron DeWitte, Eric Douglas, Craig Erick- Catfish Keith Patrick Hazell Chicago Rick Lussie Perry Welsh son, Tommy ‘T-Bone’ Giblin, BillyLee Janey, Craig Erickson Richie Hayward Bryce Janey, Dan ‘DJ’ Johnson, Denny Ke- Darrell Leonard Rico Cicalo kcck.org telsen, Skeeter Louis and Dennis “Daddy-O” Dartanyan Brown Ron DeWitte McMurrin. Post jam at Checkers Tavern! Del Saxman Jones Ron McClain Dennis McMurrin Ronnie Brewer Eddie Haywood Rose Marie Web- Ella Ruth Piggee ster Friday Blues- In this July 2013 issue — Elvin Bishop Sam Salomone • 6-10 PM - The Big Mo Blues Show Ernie Peniston Scott Cochran Eugene Jackson Sid Wingfield • 10-11 PM - Backstage Blues Scott Holt at Bluesmore 20! Fred Walk Speck Redd • 11 PM to midnight - KCCK Jams Chris Duarte at Parlor City Pub Gary Gibson Stephen Miller • Midnight Blues CD 21st Annual Bowlful of Blues Gary Jackson Steve George Saturday Blues - George Davis Steve Hayes Dr. Phil reviews: Cash Box Kings Gilbert Davis Tom Giblin • 6-10 PM - Da Blues with Bobby D Grant Townsell Willis Dobbins • 10-11 PM - The Crawfish Circuit -

Download Resume
216 S Edgar Street [email protected] Kane, PA 16735 814.366.1085 Profile: Self-taught blues/rock guitarist Regional/National touring artist Influences: Jimi Hendrix Stevie Ray Vaughan Kenny Wayne Shepherd Mato Nanji Doyle Bramhall II National Act Kenny Wayne Shepherd (5X) Openings: Mato Nanji & Indigenous (2X) Ana Popovic (4X) Samantha Fish Stephen Stills Chris Layton Joe Lewis Walker Bernard Allison Jimmy Thackery Chris Duarte Popa Chubby Molly Hatchet .38 Special Recordings: The Long Hard Road (2000) Bottle Full of Blues (2015) 9 Miles to Nowhere (2017) Awards: Endorsement with Zemaitis Guitars 2018 Semifinalist at Memphis International Blues Challenge 2019 Qualifier for Memphis International Blues Challenge 9 Miles to Nowhere named 2017 Best Self-Produced CD by Blues Society of Western PA Pittsburgh, PA; forwarded to IBC in Memphis 9 Miles to Nowhere named 2017 Album of Year by Rock Erie Music Awards (REMA’s) Erie, PA Jeff Fetterman Band named 2017 Best Blues Band of the Year at REMA’s Bottle Full of Blues named Best Self-Produced CD in 2016 by Billtown Blues Society of Williamsport, PA; forwarded to IBC in Memphis Three-song publishing deal with Transition Music in California Music in televisions: NBC’s The Passions, TNT’s The Closer Music in film: Spanish released The Tough Guy WREO Ohio radio: Best Up and Coming Blues/Rock Guitarist ASCAP Plus Awards music scholarship Dirty Dog Live TV show appearance (cable show that airs in 5 states) Recent Erie Harley Bike Festival , PA Erie Wild Rib Music Festival, PA Festivals: Jack’s Mountain -

Blues Notes March 2016
VOLUME TWENTY-ONE, NUMBER THREE • MARCH 2016 and Nick Lowe Thursday, March 10th Holland Performing Arts Center www.ticketomaha.com for tix Monday March 28th @ 6pm Zoo Bar, Lincoln SAMANTHA March 3rd .................................................. Chris Duarte Group ($10) March 5th (Sat. 8 pm) ....Kris Lager Band ($10 With First Drink Free) FISH March 10th .......................................................... Johnny Rawls ($10) March 12th ................................................................................... TBA Thursday March 17th .............................St Pat’s with The Joe Krown Trio ($10) March 19th (Sat. 8 pm) ..................................... Samantha Fish ($15) March 17th @ 6 pm March 24th .................................................. 24th Street Wailers ($10) Zoo Bar, Lincoln March 26th (Sat. 8 pm) .............................. Katy G and the Girls($10) March 31st ......................................... Ghost Town Blues Band ($10) Saturday April 2nd (Sat. 8 pm) .....................Laura Rain and the Caesars ($10) March 19th @ 8 pm April 7th .......................................Eddy “The Chief” Clearwater ($15) 21st Saloon, Omaha April 9th (Sat. 8 pm) .......................The Harlis SweetwaterBand($10) April 14th .................................................... Selwyn Birchwood ($10) PAGE 2 BLUES NEWS • BLUES SOCIETY OF OMAHA Please consider switching to the GREEN VERSION of Blues Notes. You will be saving the planet while saving BSO some expense. Contact Sher Dostal at [email protected] to switch to e-mail delivery and get the scoop days before snail mail members! BLUES ON THE RADIO: Mondays 1pm-3pm on KIOS 91.5 “Blues in the Afternoon” with Mike Jacobs You can listen to the live stream at www.kios.org Sundays 9am-Noon on KIWR 89.7 Rick Galusha’s “PS Blues” Pacific Street Blues & Americana podcast: http://kiwrblues.podOmatic.com/entry/2010-02-03T11_00_49-08_00 Lincoln’s KZUM Radio - Nebraska’s only community radio, and you can listen to it on the web at KZUM.org. -
Locals Trek to Tallahassee
Project1:Layout 1 6/10/2014 1:13 PM Page 1 NCAA: FSU battles Colorado for spot in the Sweet 16 /B1 TUESDAY TODAY CITRUSCOUNTY & next morning HIGH 77 Partly sunny and LOW warmer. 55 PAGE A4 www.chronicleonline.com MARCH 23, 2021 Florida’s Best Community Newspaper Serving Florida’s Best Community $1 VOL. 126 ISSUE 166 NEWS BRIEFS Locals trek to Tallahassee Citrus County COVID-19 cases Annual pow-wow with state officials smaller this year due to COVID-19 According to the Flor- ida Department of Health, MICHAEL D. community leaders to Expansion program. This year, again be- visitors, according to three positive cases were BATES travel to the state Capitol For one thing, only cause of COVID, move- Prendergast. The House reported in Citrus County Staff writer to try and secure funding about 45 people are going ment within the Capitol side is open by appoint- since the latest update. for needed projects here to all or part of the doings has been restricted. In- ment only to one person No new deaths were re- It’s time for Citrus at home. on Wednesday and Thurs- stead, smaller local at a time who must be ac- ported, for a total of 420. County Legislative Days “It will look very differ- day, compared to the nor- groups will meet state companied by a staff once again and, even To date in the county, ent this year but I think it mal 100 or so. The officials in various member from entrance to though the pandemic has 10,159 people have will be successful,” said chamber typically char- spots in downtown exit, with no “wandering” changed some of the nor- Ardath Prendergast, ters a bus to take the con- Tallahassee. -

Pete Neuman & the Real Deal
door. She explains He just blew my mind. He made me feel things I didnt know what to do with. The music spoke to parts of me that had never been addressed. All shows begin at 6:30 It opened up some other place in me, like letting In case of inclement weather, Tuesday Night Blues oxygen into a sealed crypt for the first time. be held at the House of Rock, 422 Water Street. The enlightened teenager started hitting blues *August 7 will be held at Phoenix Park. shows throughout the Minneapolis/Chicago/Detroit triangle. Johnny Copeland and Albert Collins May 29 The Sue Orfield Band became favorites as did the early funk and R&B of the SueOrfield.com June 5 Revolver thriving local scene including one particular July 10, 2012 at Owen Park RevolverBand.net emerging artist who called himself Prince long before June 12 Howard ‘Guitar’ Luedtke & Blue Max he took the citys sound nationwide. As with the HowardLuedtke.com beginning of the music itself, Janiva started listening June 19 Rhythm Posse to and singing the blues for catharsis. After facebook.com/RhythmPosse discovering she could sing not only for healing but to June 26 Code Blue with Catya & Sue Catya.net get paid, she went to work as a backup vocalist July 3 Mojo Lemon working frequently with Sounds of Blackness member MojoLemon.com Joanne Hollis. Janiva replaced one habit for another July 10 Pete Neuman and the Real Deal and made a run at a life as a blues musician. She PeteNeuman.com landed in the sunnier Phoenix, Arizona and took up a July 17 The Jones Tones mentor in Bob Tate, Sam Cookes legendary and long- Real Deal AMBlues.com July 24 Steve Meyer with the True Heat Band time musical director. -

Chrome Lounge Thursday, March 8Th @ 6 Pm
VOLUME TWENTY-THREE, NUMBER THREE • MARCH 2018 JEFF JENSEN Chrome Lounge Thursday, March 8th @ 6 pm Celebration of BRAD CORDLE’S life with live music Sunday, March 4th 3 pm-7 pm at Chrome Lounge WITH THE REDWOODS Thursday, March 1st @ 5:30 pm TAB BENOIT WITH THE JIMMYS Chrome Lounge, Omaha Thursday, April 12th @ 6 pm, Chrome Lounge, Omaha Advance Tix @ www.evetbrite.com CHRIS DUARTE Tuesday March 20 @ 6 pm Chrome Zoo Bar, Lincoln Wednesday Lounge March 21 @ 7 pm 8552 Park Drive, Omaha (w/ Hector Anchondo Band) 402-339-8660 Lookout Lounge The Blues Society of Omaha Presents 320 S. 72nd St., Omaha Legendary Thursday Blues Matinees and more All shows 6 pm unless noted otherwise Thursday, March 1st (5:30 pm) ............ The Brian England Groove Prescription with The Redwoods ($10) Thursday, March 8th ..................................Jeff Jensen Band ($10) Thursday, March 15th .................................Sugaray Rayford ($15) Thursday, March 22nd ....................................... The Bel Airs ($10) Saturday, March 24th ................The Johnny Winter All-Star Band plus “Down & Dirty” documentary film about Johnny Winter’s life & career ($15) Thursday, March 29th ......Chris Ruest Band featuring Gene Taylor Thursday, April 5th ................ Lil’ Ed and the Blues Imperials ($12) Thursday, April 12th ...........Tab Benoit with The Jimmys ($25/$30) Saturday, March 24th @ 6 pm • Chrome Lounge, Omaha PAGE 2 BLUES NEWS • BLUES SOCIETY OF OMAHA Why Join the Blues Society Of Omaha with Your Membership Donation? The Blues Society of Omaha, Inc. is a 501(c)(3) non-profit organization formed in 1998. We are an all-volunteer organization with over 800 dues-paying members. -

Mark Cloutier
Mark Cloutier Song Samples: Mark Cloutier Radio Sign-up at http://www.radiosubmit.com to download songs for free. 2012 NYS Blues Fest "Guitarists Mark Cloutier and John Hart traded riffs until Hart snapped a string, quickly swapping out guitars and jumping back into the jam. Tunes went from smooth and sexy, thanks to the dark fifth, Cloutier explained, to whammy-powered and grinding with some slide in between. Hendrix, B.B. King and Muddy Waters all got recognized and drawn from throughout the set, one that wrapped up rough and raw, just as some dirty, double barrel blues should." Jessica Novak --Syracuse New Times---2012 NY State Blues Fest http://www.nysbluesfest.com/ Mwe3 Guitar Magazine writes:: "Cloutier is a guitarist sounding clearly inspired by rock guitar greats like Jimi Hendrix and Johnny Winter as well as more traditional blues, R&B and jazz guitarists as diverse as Buddy Guy, Steve Cropper, Robin Trower and Kenny Burrell. In other words, Cloutier is a guitarist who's not afraid to break through with a hard rock riff before moving on to jazzing things up when he has to." ***************************************************************************************** John Hart's splendid song writing and unique singing style (not to mention his swinging guitar groove and slide work) make this band one of a kind. He seems to have lived every note he sings. The Double Barrel Blues Band is a modern blues group taking traditional blues and rock n’ roll and giving birth to an new era in music. Their signature double guitar sound (Mark Cloutier and John Hart) is well known in music circles. -

Master Methode
BOOK + CD + DVD 50 Blues Rhythms for Guitar CONTENTS With its 50 Blues rhythms inspired by the biggest hits of the greatest guitarists of all time (Eric Clapton, Buddy Guy, Albert King, Muddy Waters, Stevie Ray Vaughan, Robert Cray, Albert Collins, B.B. King, T-Bone Walker etc.), this tutorial will keep you pleasantly busy for quite a while. But there’s more to it than that! Besides affording pleasure, these rhythms allow you to discover and study the tools required for a good Blues accompaniment: triads, double stops, single notes, bends, barre chords, slides, hammer-ons, pull-offs, rest strokes, binary and shuffle rhythms, etc. All this is included in the guidelines given to you in the preliminary chapter – guidelines regarding the structure, the rhythm, as well as the chords employed. The DVD attached to the tutorial offers you the possibility to mindfully observe all 50 rhythms – first at actual playing speed, then at a slower speed. This again gives you the opportunity to closely follow the movement of the hands, to choose the right fingerings and keep a steady beat(!) For its part, the mp3 CD is composed of as many backing tracks as there are rhythms in the tutorial; the 50 backing tracks are recorded at two different tempi: the intended tempo (actual playing speed) and the rehearsal tempo (slower speed). The backing tracks provided here are of an appropriate length (about 4 to 5 minutes each, which sums up to almost 7 h of musical practice). This means that you have enough time at your disposal to practice under the best conditions.