DOCSLIB.ORG

Dmol Guide to Select a Dmol3 Task 1

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Dmol Guide to Select a Dmol3 Task 1 DMOL3 GUIDE MATERIALS STUDIO 8.0 Copyright Notice ©2014 Dassault Systèmes. All rights reserved. 3DEXPERIENCE, the Compass icon and the 3DS logo, CATIA, SOLIDWORKS, ENOVIA, DELMIA, SIMULIA, GEOVIA, EXALEAD, 3D VIA, BIOVIA and NETVIBES are commercial trademarks or registered trademarks of Dassault Systèmes or its subsidiaries in the U.S. and/or other countries. All other trademarks are owned by their respective owners. Use of any Dassault Systèmes or its subsidiaries trademarks is subject to their express written approval. Acknowledgments and References To print photographs or files of computational results (figures and/or data) obtained using BIOVIA software, acknowledge the source in an appropriate format. For example: "Computational results obtained using software programs from Dassault Systèmes Biovia Corp.. The ab initio calculations were performed with the DMol3 program, and graphical displays generated with Materials Studio." BIOVIA may grant permission to republish or reprint its copyrighted materials. Requests should be submitted to BIOVIA Support, either through electronic mail to [email protected], or in writing to: BIOVIA Support 5005 Wateridge Vista Drive, San Diego, CA 92121 USA Contents DMol3 1 Setting up a molecular dynamics calculation20 Introduction 1 Choosing an ensemble 21 Further Information 1 Defining the time step 21 Tasks in DMol3 2 Defining the thermostat control 21 Energy 3 Constraints during dynamics 21 Setting up the calculation 3 Setting up a transition state calculation 22 Dynamics 4 Which method to use? 22 Selecting the thermodynamic ensemble 4 Verifying a transition state 22 Defining the time step 4 Setting up a TS confirmation calculation 23 Controlling the thermostat 4 Setting up a work function calculation 23 Constraints during dynamics 4 Setting up an elastic constants calculation 24 Transition state searching 5 Parameters for the optimization 24 Transition state optimization 6 Setting up a reaction kinetics calculation 24 Transition state searching by synchronous Transition state search 25 transit methods 6 Hessian calculation 25 Verifying a transition state 7 Reaction rate calculation 25 Transition state searching via synchronous Setting up an electron transport calculation 25 transit methods 7 Requesting electronic and structural Input to a synchronous transit calculation 8 properties 26 Restarting a QST calculation 9 Setting up electron densities 27 Transition state searching via eigenvector Setting up electrostatics 27 following 9 Setting up vibrational frequencies 28 Calculation parameters 9 Setting up Raman intensities 28 Use of the Hessian 9 Setting up Fukui functions 28 Geometry optimization 9 Setting up molecular orbital analysis 29 Following a reaction path 10 Setting up a population analysis 29 Elastic constants 11 Setting up band structures 30 Reaction kinetics 11 Setting up density of states 30 Electron Transport 12 Setting up Fermi surfaces 31 Electrodes 12 Setting up COSMO Sigma profile Properties 13 calculation 31 Setting up DMol3 calculations 13 Setting up an optics calculation 31 Setting up electronic options 14 Manipulating files 32 Integration accuracy 14 Input files 32 SCF tolerance 14 Output files 33 k-points 14 Restarting a DMol3 calculation 33 Core treatment 14 Importing a Hessian file 35 Real space cutoff 15 Analyzing DMol3 results 35 Harris approximation 17 Updating structure 36 Solvation scheme 17 Displaying trajectory and chart data 37 Performance tips 18 Creating a trajectory and chart 37 Setting up k-points 18 Animating the trajectory 38 Setting up a geometry optimization 19 Chart Viewer point selection 38 Algorithms for the optimization 20 Visualizing volumetric data 38 Parameters for the optimization 20 Electron density 38 Electrostatic potential 39 Meta-GGA functionals 63 Fukui functions 40 Numerical basis sets 63 Molecular orbitals 40 Atomic basis sets are generated Field visualization 41 numerically 63 Visualizing Fermi surfaces 42 Advantages of numerically derived basis sets 63 Displaying population analysis results 42 Additional basis functions, including Displaying computed charges, spins, and polarization 63 bond orders 43 Numerical integration 65 Displaying band structure charts 43 Atomic and molecular integration grids 65 Displaying density of states charts 44 Integration points, atomic size, precision, Full density of states 45 and computational cost 65 Partial density of states 45 Atomic shells 66 Calculating elastic constants 46 Assuring consistent precision during Displaying the averaged potential chart for integration 66 work function calculations 46 Partition functions improve convergence Analyzing optical properties 47 and avoid nuclear cusps 66 Displaying Raman spectra 48 Pseudopotentials 67 Calculating reaction kinetics 48 Norm-conserving pseudopotentials 68 Displaying solvation properties 49 Evaluating the Coulombic potential Analyzing current and transmission numerically 69 properties 50 The model charge density 70 DMol3 jobs 51 Effect of angular truncation on precision Using DMol3 job control 51 of model charge density 70 Remote DMol3 jobs 51 The Coulombic potential 70 A sample DMol3 run 51 The total potential 70 Computational self-consistent field If a remote DMol3 job fails 53 procedure 70 Running DMol3 in standalone mode 54 Interpolating the numerical atomic bases DMol3 file formats 57 onto the molecular grid 70 DMol3 file formats - ARC 58 Constructing the initial molecular electron DMol3 file formats - BANDS 58 density 71 DMol3 file formats - CAR and MDF 58 Additional computational costs 71 DMol3 file formats - COSMO 58 Reducing the computational cost 71 DMol3 file formats - GRD 59 Damping and convergence 71 DMol3 file formats - HESSIAN 59 Efficiently calculating the electrostatic potential 71 DMol3 file formats - HESSWK 59 Effect of auxiliary density approximation DMol3 file formats - INPUT 60 on accuracy of calculated total energy 72 DMol3 file formats - OCCUP 60 SCF convergence acceleration by DIIS 72 DMol3 file formats - OUTMOL 60 Energy gradients 73 DMol3 file formats - PDOS_WEIGHTS 61 Predicting chemical structure 73 DMol3 file formats - TPVEC 61 First derivative of total energy with DMol3 file formats - TPDENSK 61 respect to change in nuclear position 73 Reaction Kinetics Study Table 61 Derivative of the basis function 74 Theory in DMol3 62 Derivation of other terms 74 Density functional theory (DFT) in DMol3 62 The final equation for the derivative of the Functionals in DMol3 62 energy 75 Local functionals 62 Computational costs 75 Nonlocal functionals 62 Potential problems 75 Hybrid functionals 62 Minimization algorithms; molecular DMol3 TS Optimization dialog 105 symmetry 75 DMol3 TS Confirmation dialog 105 Electronic excitations with TD-DFT 75 DMol3 Elastic Constants dialog 106 Predicting UV-Vis spectra 75 DMol3 Reaction Kinetics dialog 107 Computational costs 76 DMol3 Transport dialog 109 Accuracy of excitation energies and orbital Setup tab 110 overlap 77 Density Mixing 110 TD-DFT in combination with hybrid functionals in DMol3 77 Electrode 111 Molecular dynamics 77 DMol3 Transmission dialog 111 Ensembles 77 DMol3 Current/Voltage dialog 111 NVE ensemble 78 Electrodes tab 111 NVT dynamics 78 Electrostatics tab 112 Constraints 79 DMol3 Poisson Boundary Conditions dialog 112 Point group symmetry 80 Electronic tab 113 COSMO-solvation effects 80 DMol3 Electronic Options dialog 115 DMol3/COSMO 82 SCF tab 116 Determination of the cavity surface (or solvent-accessible surface) 83 k-points tab 117 Determination of non-electrostatic Orbital Cutoff tab 118 contributions to the free energy of Solvent tab 119 solvation 83 DFT-D tab 120 COSMO-SAC model 83 Properties tab 121 COSMO sigma profile 84 Band structure selection 122 Electric field gradients 84 Density of states selection 122 Thermodynamic calculations 86 DMol3 Density of States Options Enthalpy 86 dialog 123 Entropy 87 Electron density selection 124 Heat capacity 87 Electrostatics selection 125 Using the results 88 Frequency selection 125 Fitting atomic point charges to the Partial Hessian dialog 126 electrostatic potential (ESP) 88 Fukui function selection 127 Mulliken and Mayer bond orders 89 Optics selection 127 Hirshfeld charge analysis 90 DMol3 Optics Options dialog 128 Fukui functions 91 Orbitals selection 129 Raman spectra 92 Population analysis selection 129 Basis set superposition error 93 DMol3 Grid Parameters dialog 130 Converging SCF 93 Job Control tab 131 Challenging systems 94 DMol3 Job Control Options dialog 132 Checklist 94 DMol3 Job Files dialog 133 Dialogs in DMol3 96 DMol3 Analysis dialog 133 DMol3 Calculation dialog 96 Band structure selection 134 Setup tab 96 Current/Voltage selection 135 DMol3 Energy dialog 99 Density of states selection 136 DMol3 Geometry Optimization dialog 100 DMol3 DOS Analysis Options dialog 137 DMol3 Dynamics dialog 101 Elastic constants selection 138 Dynamics tab 102 Electron density selection 138 Thermostat tab 102 Energy evolution selection 139 DMol3 Transition State Search dialog 103 Fermi surface selection 139 Fukui function selection 140 Optics selection 141 DMol3 Optics Analysis Options dialog 141 Orbitals selection 142 Population analysis selection 143 Potentials selection 144 Raman spectrum selection 144 Reaction kinetics selection 145 Solvation properties selection 146 Choose COSMO File dialog 146 Structure selection 147 Thermodynamic properties selection 147 Transmission selection 148 DMol3 keywords 149 DMol3 References 150 DMol3 Introduction DMol3 allows you to model the electronic structure and energetics of molecules,
Load more

Recommended publications
  • Spoken Tutorial Project, IIT Bombay Brochure for Chemistry Department
    Spoken Tutorial Project, IIT Bombay Brochure for Chemistry Department Name of FOSS Applications Employability GChemPaint GChemPaint is an editor for 2Dchem- GChemPaint is currently being developed ical structures with a multiple docu- as part of The Chemistry Development ment interface. Kit, and a Standard Widget Tool kit- based GChemPaint application is being developed, as part of Bioclipse. Jmol Jmol applet is used to explore the Jmol is a free, open source molecule viewer structure of molecules. Jmol applet is for students, educators, and researchers used to depict X-ray structures in chemistry and biochemistry. It is cross- platform, running on Windows, Mac OS X, and Linux/Unix systems. For PG Students LaTeX Document markup language and Value addition to academic Skills set. preparation system for Tex typesetting Essential for International paper presentation and scientific journals. For PG student for their project work Scilab Scientific Computation package for Value addition in technical problem numerical computations solving via use of computational methods for engineering problems, Applicable in Chemical, ECE, Electrical, Electronics, Civil, Mechanical, Mathematics etc. For PG student who are taking Physical Chemistry Avogadro Avogadro is a free and open source, Research and Development in Chemistry, advanced molecule editor and Pharmacist and University lecturers. visualizer designed for cross-platform use in computational chemistry, molecular modeling, material science, bioinformatics, etc. Spoken Tutorial Project, IIT Bombay Brochure for Commerce and Commerce IT Name of FOSS Applications / Employability LibreOffice – Writer, Calc, Writing letters, documents, creating spreadsheets, tables, Impress making presentations, desktop publishing LibreOffice – Base, Draw, Managing databases, Drawing, doing simple Mathematical Math operations For Commerce IT Students Drupal Drupal is a free and open source content management system (CMS).
    [Show full text]
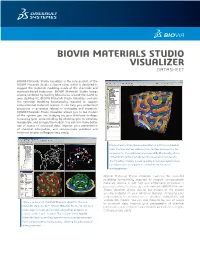
  • Biovia Materials Studio Visualizer Datasheet
    BIOVIA MATERIALS STUDIO VISUALIZER DATASHEET BIOVIA Materials Studio Visualizer is the core product of the BIOVIA Materials Studio software suite, which is designed to support the materials modeling needs of the chemicals and materials-based industries. BIOVIA Materials Studio brings science validated by leading laboratories around the world to your desktop PC. BIOVIA Materials Studio Visualizer contains the essential modeling functionality required to support computational materials science. It can help you understand properties or processes related to molecules and materials. BIOVIA Materials Studio Visualizer allows you to see models of the system you are studying on your Windows desktop, increasing your understanding by allowing you to visualize, manipulate, and analyze the models. You can also make better use of access to structural data, improve your presentation of chemical information, and communicate problems and solutions to your colleagues very easily. Image of early-stage phase segregation in a diblock copolymer melt. The blue surface indicates the interface between the two components. The volume is colormapped by the density of one of the blocks, red being high density, blue being low-density. The MesoDyn module is used to study these large systems over long-times such as required to observe these structural rearrangements. BIOVIA Materials Studio Visualizer contains the essential modeling functionality required to support computational materials science. It can help you understand properties or processes related to molecules and materials. BIOVIA Materials Studio Visualizer allows you to see models of the system you are studying on your Windows desktop, increasing your understanding by allowing you to visualize, manipulate, and analyze the models.
    [Show full text]
  • Download Author Version (PDF)
    PCCP Accepted Manuscript This is an Accepted Manuscript, which has been through the Royal Society of Chemistry peer review process and has been accepted for publication. Accepted Manuscripts are published online shortly after acceptance, before technical editing, formatting and proof reading. Using this free service, authors can make their results available to the community, in citable form, before we publish the edited article. We will replace this Accepted Manuscript with the edited and formatted Advance Article as soon as it is available. You can find more information about Accepted Manuscripts in the Information for Authors. Please note that technical editing may introduce minor changes to the text and/or graphics, which may alter content. The journal’s standard Terms & Conditions and the Ethical guidelines still apply. In no event shall the Royal Society of Chemistry be held responsible for any errors or omissions in this Accepted Manuscript or any consequences arising from the use of any information it contains. www.rsc.org/pccp Page 1 of 11 PhysicalPlease Chemistry do not adjust Chemical margins Physics PCCP PAPER Effect of nanosize on surface properties of NiO nanoparticles for adsorption of Quinolin-65 ab a a Received 00th January 20xx, Nedal N. Marei, Nashaat N. Nassar* and Gerardo Vitale Accepted 00th January 20xx Using Quinolin-65 (Q-65) as a model-adsorbing compound for polar heavy hydrocarbons, the nanosize effect of NiO Manuscript DOI: 10.1039/x0xx00000x nanoparticles on adsorption of Q-65 was investigated. Different-sized NiO nanoparticles with sizes between 5 and 80 nm were prepared by controlled thermal dehydroxylation of Ni(OH)2.
    [Show full text]
  • Supporting Information
    Electronic Supplementary Material (ESI) for Chemical Science. This journal is © The Royal Society of Chemistry 2015 Supporting Information A Single Crystalline Porphyrinic Titanium Metal−Organic Framework Shuai Yuana†, Tian-Fu Liua†, Dawei Fenga, Jian Tiana, Kecheng Wanga, Junsheng Qina, a a a a b Qiang Zhang , Ying-Pin Chen , Mathieu Bosch , Lanfang Zou , Simon J. Teat, Scott J. c a Dalgarno and Hong-Cai Zhou * a Department of Chemistry, Texas A&M University, College Station, Texas 77842-3012, USA b Advanced Light Source, Lawrence Berkeley National Laboratory Berkeley, CA 94720, USA c Institute of Chemical Sciences, Heriot-Watt University Riccarton, Edinburgh EH14 4AS, U.K. † Equal contribution to this work *To whom correspondence should be addressed. Email: [email protected] Tel: +1 (979) 845-4034; Fax: +1 (979) 845-1595 S1 Contents S1. Ligand Synthesis..............................................................................................................3 S2. Syntheses of PCN-22.......................................................................................................5 S3. X-ray Crystallography .....................................................................................................6 S4. Topological Analyses ......................................................................................................9 S5. N2 Sorption Isotherm .....................................................................................................10 S6. Simulation of the Accessible Surface Area ...................................................................12
    [Show full text]
  • PDF Hosted at the Radboud Repository of the Radboud University Nijmegen
    PDF hosted at the Radboud Repository of the Radboud University Nijmegen The following full text is a publisher's version. For additional information about this publication click this link. http://hdl.handle.net/2066/19078 Please be advised that this information was generated on 2021-09-23 and may be subject to change. Computational Chemistry Metho ds Applications to Racemate Resolution and Radical Cation Chemistry ISBN Computational Chemistry Metho ds Applications to Racemate Resolution and Radical Cation Chemistry een wetenschapp elijkeproeve op het gebied van de Natuurwetenschapp en Wiskunde en Informatica Pro efschrift ter verkrijging van de graad van do ctor aan de KatholiekeUniversiteit Nijmegen volgens b esluit van het College van Decanen in het op enbaar te verdedigen op dinsdag januari des namiddags om uur precies do or Gijsb ert Schaftenaar geb oren op augustus te Harderwijk Promotores Prof dr ir A van der Avoird Prof dr E Vlieg Copromotor Prof dr RJ Meier Leden manuscriptcommissie Prof dr G Vriend Prof dr RA de Gro ot Dr ir PES Wormer The research rep orted in this thesis was nancially supp orted by the Dutch Or ganization for the Advancement of Science NWO and DSM Contents Preface Intro duction Intro duction Chirality Metho ds for obtaining pure enantiomers Racemate Resolution via diastereomeric salt formation Rationalization of diastereomeric salt formation Computational metho ds for mo deling the lattice energy Molecular Mechanics Quantum Chemical
    [Show full text]
  • Reactive Molecular Dynamics Study of the Thermal Decomposition of Phenolic Resins
    Article Reactive Molecular Dynamics Study of the Thermal Decomposition of Phenolic Resins Marcus Purse 1, Grace Edmund 1, Stephen Hall 1, Brendan Howlin 1,* , Ian Hamerton 2 and Stephen Till 3 1 Department of Chemistry, Faculty of Engineering and Physical Sciences, University of Surrey, Guilford, Surrey GU2 7XH, UK; [email protected] (M.P.); [email protected] (G.E.); [email protected] (S.H.) 2 Bristol Composites Institute (ACCIS), Department of Aerospace Engineering, School of Civil, Aerospace, and Mechanical Engineering, University of Bristol, Bristol BS8 1TR, UK; [email protected] 3 Defence Science and Technology Laboratory, Porton Down, Salisbury SP4 0JQ, UK; [email protected] * Correspondence: [email protected]; Tel.: +44-1483-686-248 Received: 6 March 2019; Accepted: 23 March 2019; Published: 28 March 2019 Abstract: The thermal decomposition of polyphenolic resins was studied by reactive molecular dynamics (RMD) simulation at elevated temperatures. Atomistic models of the polyphenolic resins to be used in the RMD were constructed using an automatic method which calls routines from the software package Materials Studio. In order to validate the models, simulated densities and heat capacities were compared with experimental values. The most suitable combination of force field and thermostat for this system was the Forcite force field with the Nosé–Hoover thermostat, which gave values of heat capacity closest to those of the experimental values. Simulated densities approached a final density of 1.05–1.08 g/cm3 which compared favorably with the experimental values of 1.16–1.21 g/cm3 for phenol-formaldehyde resins.
    [Show full text]
  • Pymol Modelling Workshop
    PyMOL Modelling Workshop My website: http://pldserver1.biochem.queensu.ca/~rlc/work/teaching/BCHM442/ There you will find links to download the latest educational version of PyMOL as well as a link to my “Introduction to PyMOL”, which in turn has links to other people's PyMOL tutorials. Note also the PyMOL Wiki: http://pymolwiki.org. Structure files can be found by searching the Protein Data Bank (PDB) for structure: easy to remember website http://www.pdb.org. There is also the PDBe (PDB Europe, http://www.pdbe.org) that contains the same databank of structures, but with a different web interface for searching for structures and a different set of tools for analyzing structures. What is in a PDB file? Lots of information in the “header” (the section of the file preceding the actual atomic coordinates) as well as the coordinates for the atoms. When assessing a structure, one needs to take account of the resolution and R-factor, error estimates and missing residues. There is information about the sequence that was used to determine the structure with a sequence database reference. There is also information about the biological unit. In the case of crystal structures the biological unit may need to be generated by applying crystallographic symmetry operators, although there are web sites that also try to provide that information. (e.g. http://www.ebi.ac.uk/msd-srv/pisa/). Warning: One cannot blindly trust a crystal structure to be providing you with a completely accurate picture of reality. Reading the paper that describes the structure is a good start! Outline of PyMOL usage PyMOL is a very powerful, scriptable (customizable) tool for making publication-quality figures and performing analyses on structures.
    [Show full text]
  • Density Functional Theory (DFT)
    Herramientas mecano-cuánticas basadas en DFT para el estudio de moléculas y materiales en Materials Studio 7.0 Javier Ramos Biophysics of Macromolecular Systems group (BIOPHYM) Departamento de Física Macromolecular Instituto de Estructura de la Materia – CSIC [email protected] Webinar, 26 de Junio 2014 Anteriores webinars Como conseguir los videos y las presentaciones de anteriores webminars: Linkedin: Grupo de Química Computacional http://www.linkedin.com/groups/Química-computacional-7487634 Índice Density Functional Theory (DFT) The Jacob’s ladder DFT modules in Maretials Studio DMOL3, CASTEP and ONETEP XC functionals Basis functions Interfaces in Materials Studio Tasks Properties Example: n-butane conformations Density Functional Theory (DFT) DFT is built around the premise that the energy of an electronic system can be defined in terms of its electron probability density (ρ). (Hohenberg-Kohn Theorem) E 0 [ 0 ] Te [ 0 ] E ne [ 0 ] E ee [ 0 ] (easy) Kinetic Energy for ????? noninteracting (r )v (r ) dr electrons(easy) 1 E[]()()[]1 r r d r d r E e e2 1 2 1 2 X C r12 Classic Term(Coulomb) Non-classic Kohn-Sham orbitals Exchange & By minimizing the total energy functional applying the variational principle it is Correlation possible to get the SCF equations (Kohn-Sham) The Jacob’s Ladder Accurate form of XC potential Meta GGA Empirical (Fitting to Non-Empirical Generalized Gradient Approx. atomic properties) (physics rules) Local Density Approximation DFT modules in Materials Studio DMol3: Combine computational speed with the accuracy of quantum mechanical methods to predict materials properties reliably and quickly CASTEP: CASTEP offers simulation capabilities not found elsewhere, such as accurate prediction of phonon spectra, dielectric constants, and optical properties.
    [Show full text]
  • Atomistic Molecular Dynamics Simulation of Graphene- Isoprene Nanocomposites
    Atomistic molecular dynamics simulation of graphene- isoprene nanocomposites P Chanlert1, J Wong-Ekkabut2, W Liewrian3,4,5 and T Sutthibutpong3,4,5* 1 Program of Physics, Faculty of Science and Technology, Songkhla Rajabhat University, Songkhla, 90000, Thailand 2 Department of Physics, Faculty of Science, Kasetsart University, Bangkok 10900, Thailand 3 Theoretical and Computational Physics Group, Department of Physics, Faculty of Science, King Mongkut’s University of Technology Thonburi (KMUTT), Bangkok 10140, Thailand 4 Theoretical and Computational Science Center (TaCS), Science Laboratory Building, Faculty of Science, King Mongkut’s University of Technology Thonburi (KMUTT), Bangkok 10140, Thailand 5 Thailand Center of Excellence in Physics (ThEP Center), Commission on Higher Education, Bangkok 10400, Thailand *email: [email protected] Abstract. A series of atomistic molecular dynamics simulations were performed for 4-mer isoprene molecules confined between graphene sheets with varied graphene separations in order to observe the finite size effects arose from the van der Waals interactions between the isoprene oligomer, forming high density shells at the graphene interfaces. For the small confinement regions, 1.24 nm and 2.21 nm, local density of isoprene at the graphene interface becomes higher than 10 times the bulk density. These results provided the further insights towards the rational design of nanostructures based on graphene sheets and natural rubber polymer. 1. Introduction Composite material is the combination between two materials or more where chemical reaction between these materials is absent. In composites, one with higher quantity is called matrix while those with lesser quantity are called fillers. In general, adding fillers into matrix material enhances both physical and mechanical properties in some ways.
    [Show full text]
  • Prediction of Solubility of Amino Acids Based on Cosmo Calculaition
    PREDICTION OF SOLUBILITY OF AMINO ACIDS BASED ON COSMO CALCULAITION by Kaiyu Li A dissertation submitted to Johns Hopkins University in conformity with the requirement for the degree of Master of Science in Engineering Baltimore, Maryland October 2019 Abstract In order to maximize the concentration of amino acids in the culture, we need to obtain solubility of amino acid as a function of concentration of other components in the solution. This function can be obtained by calculating the activity coefficient along with solubility model. The activity coefficient of the amino acid can be calculated by UNIFAC. Due to the wide range of applications of UNIFAC, the prediction of the activity coefficient of amino acids is not very accurate. So we want to fit the parameters specific to amino acids based on the UNIFAC framework and existing solubility data. Due to the lack of solubility of amino acids in the multi-system, some interaction parameters are not available. COSMO is a widely used way to describe pairwise interactions in the solutions in the chemical industry. After suitable assumptions COSMO can calculate the pairwise interactions in the solutions, and largely reduce the complexion of quantum chemical calculation. In this paper, a method combining quantum chemistry and COSMO calculation is designed to accurately predict the solubility of amino acids in multi-component solutions in the ii absence of parameters, as a supplement to experimental data. Primary Reader and Advisor: Marc D. Donohue Secondary Reader: Gregory Aranovich iii Contents
    [Show full text]
  • Molecular Dynamics Simulations of Molecular Diffusion Equilibrium and Breakdown Mechanism of Oil-Impregnated Pressboard with Water Impurity
    polymers Article Molecular Dynamics Simulations of Molecular Diffusion Equilibrium and Breakdown Mechanism of Oil-Impregnated Pressboard with Water Impurity Yi Guan 1,2, Ming-He Chi 1,2, Wei-Feng Sun 1,2,*, Qing-Guo Chen 1,2 and Xin-Lao Wei 1,2 1 Heilongjiang Provincial Key Laboratory of Dielectric Engineering, School of Electrical and Electronic Engineering, Harbin University of Science and Technology, Harbin 150080, China; [email protected] (Y.G.); [email protected] (M.-H.C.); [email protected] (Q.-G.C.); [email protected] (X.-L.W.) 2 Key Laboratory of Engineering Dielectrics and Its Application, Ministry of Education, Harbin University of Science and Technology, Harbin 150080, China * Correspondence: [email protected]; Tel.: +86-15846592798 Received: 30 October 2018; Accepted: 15 November 2018; Published: 16 November 2018 Abstract: The water molecule migration and aggregation behaviors in oil-impregnated pressboard are investigated by molecular dynamics simulations in combination with Monte Carlo molecular simulation technique. The free energy and phase diagram of H2O-dodecylbenzene (DDB) and H2O-cellulose mixtures are calculated by Monte Carlo technique combined with the modified Flory-Huggins model, demonstrating that H2O molecules can hardly dissolved with infinitesimal content in cellulose system at temperature lower than 650 K, based on which the oil/cellulose layered structure with water impurity representing three-phase coexistence in oil-impregnated pressboard are modeled and performed for molecular dynamics. The molecular dynamics of H2O/DDB/cellulose three-phase mixture simulating oil-paper insulating system with H2O impurity indicates that DDB molecules can thermally intrude into the cellulose-water interface so as to separate the water phase and cellulose fiber.
    [Show full text]
  • What's New in Biovia Materials Studio 2020
    WHAT’S NEW IN BIOVIA MATERIALS STUDIO 2020 Datasheet BIOVIA Materials Studio 2020 is the latest release of BIOVIA’s predictive science tools for chemistry and materials science research. Materials Studio empowers researchers to understand the relationships between a material’s mo- lecular or crystal structure and its properties in order to make more informed decisions about materials research and development. More often than not materials performance is influenced by phenomena at multiple scales. Scientists using Materials Studio 2020 have an extensive suite of world class solvers and parameter sets operating from atoms to microscale for simulating more materials and more properties than ever before. Furthermore, the predicted properties can now be used in multi-physics modeling and in systems modeling software such as SIMULIA Abaqus and CATIA Dymola to predict macroscopic behaviors. In this way multiscale simulations can be used to solve some of the toughest pro- blems in materials design and product optimization. BETTER MATERIALS - BETTER BATTERIES Safe, fast charging batteries with high energy density and long life are urgently needed for a host of applications - not least for the electrification of all modes of transportation as an alternative to fossil fuel energy sources. Battery design relies on a complex interplay between thermal, mechanical and chemical processes from the smallest scales of the material (electronic structure) through to the geometry of the battery cell and pack design. Improvements to the component materials used in batteries and capacitors are fundamental to providing the advances in performance needed. Materials Studio provides new functionality to enable the simula- tion of key materials parameters for both liquid electrolytes and electrode components.
    [Show full text]