DOCSLIB.ORG

The Indifference Curve Analysis - an Alternative Approach Represented by Odes Using Geogebra

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Indifference Curve Analysis - an Alternative Approach Represented by Odes Using Geogebra The indifference curve analysis - An alternative approach represented by ODEs using GeoGebra Jorge Marques and Nuno Baeta CeBER and CISUC University of Coimbra June 26, 2018, Coimbra, Portugal 7th CADGME - Conference on Digital Tools in Mathematics Education Jorge Marques and Nuno Baeta The indifference curve analysis - An alternative approach represented by ODEs using GeoGebra Outline Summary 1 The neoclassic consumer model in Economics 2 2 Smooth Preferences on R+ Representation by a utility function Representation by the marginal rate of substitution 3 2 Characterization of Preferences Classes on R+ 4 Graphic Representation on GeoGebra Jorge Marques and Nuno Baeta The indifference curve analysis - An alternative approach represented by ODEs using GeoGebra The neoclassic consumer model in Economics Variables: Quantities and Prices N Let R+ = fx = (x1;:::; xN ): xi > 0g be the set of all bundles of N goods Xi , N ≥ 2, and Ω = fp = (p1;:::; pN ): pi > 0g be the set of all unit prices of Xi in the market. Constrained Maximization Problem The consumer is an economic agent who wants to maximize a utility function u(x) subject to the budget constraint pT x ≤ m, where m is their income. In fact, the combination of strict convex preferences with the budget constraint ensures that the ∗ ∗ problem has a unique solution, a bundle of goods x = (xi ) ∗ i such that xi = d (p1;:::; pN ; m). System of Demand Functions In this system quantities are taken as functions of their market prices and income. Jorge Marques and Nuno Baeta The indifference curve analysis - An alternative approach represented by ODEs using GeoGebra The neoclassic consumer model in Economics Economic Theory of Market Behavior However, a utility function has been regarded as unobservable in the sense of being beyond the limits of the economist’s knowledge. The economic theory has testable consequences, that is, the observations (empirical data) can confirm the theoretical predictions. Assuming that theory is not disproved, can we recover the preferences (or utility) from the observations (prices, quantities and income)? We have an inverse problem: given a differentiable map N d :Ω × R+ −! R+ (p; m) 7−! x = d(p; m) can one find a utility function u(x) such that x∗ = d(p; m) is the system of demand functions for the maximization problem? Jorge Marques and Nuno Baeta The indifference curve analysis - An alternative approach represented by ODEs using GeoGebra The neoclassic consumer model in Economics The Problem of Integrability in Utility Theory (Samuelson, 1950) That question of the existence of a utility function is known as the integrability problem in economics. Ordinal Utility Utility functions are invariant by increasing transformations g. Economic Assumptions A utility function u must be: Increasing since the consumer prefers more rather than fewer goods. So that the marginal utility of a good is positive (It is measured by the rate of change of u). Strictly quasiconcave by the principle of diminishing marginal utility: If the consumption of one good increases then its marginal utility decreases, holding the consumption of the other goods constant. Jorge Marques and Nuno Baeta The indifference curve analysis - An alternative approach represented by ODEs using GeoGebra The neoclassic consumer model in Economics Mathematical Integration We have to deal with a mathematical problem which consists in solving an ordinary differential equation (ODE) or a system of partial differential equations (PDEs) . Mathematical Solving If N = 2 then the existence of a utility function is guaranteed since an ODE always admits an integrating factor. Otherwise, it is only possible to find an integrating factor for a system of PDEs provided that it holds the integrability conditions, hence there exists a utility function under appropriate conditions. Jorge Marques and Nuno Baeta The indifference curve analysis - An alternative approach represented by ODEs using GeoGebra 2 Smooth Preferences on R+ 2 Consumer’s Preferences on R+ 2 2 Let R+ = f(x; y) 2 R : x > 0 ^ y > 0g be the set of all bundles of two goods X and Y . Given any two bundles P1 = (x1; y1) and P2 = (x2; y2), an individual consumer can take one of three choices: i) He (or she) will prefer P1 to P2, P1 P2 ii) He (or she) will prefer P2 to P1, P2 P1 iii) He (or she) will be indifferent, P1 ∼ P2. Mathematical Formulation So an individual consumer is assumed to have a preference 2 relation on R+ represented by a binary relation which satisfies three axioms: reflexivity, transitivity and completeness. The axioms of continuity, monotonicity and strict convexity are usually imposed on in the differentiable setting (Mas-Colell, 1995). Jorge Marques and Nuno Baeta The indifference curve analysis - An alternative approach represented by ODEs using GeoGebra 2 Smooth Preferences on R+ Methodology - Distinct Approaches In the neoclassical approach, it is defined a representation that requires the determination of an arbitrary utility function of class C2. A utility function aims to construct a ranking of choices based on the consumer’s preferences relation. In our work we consider a representation using an exchange rate between two goods, called marginal rate of substitution, in order to describe smooth preferences. In our approach, If we use this rate then we can determine a utility representation for consumer’s preferences. Jorge Marques and Nuno Baeta The indifference curve analysis - An alternative approach represented by ODEs using GeoGebra Representation by a marginal rate of substitution Economic Interpretation It was Hicks who introduced the concept of marginal rate of substitution between two goods as an incremental amount of one good that the consumer is willing to give up in order to gain an incremental increase of consumption of other good. Marginal Rate of Substitution as a Primitive Concept Suppose now that a utility function of class C2 is unknown. Assuming that Y is a reference good, without loss of generality, then the preferences can be represented by the marginal rate of substitution of Y for X. Jorge Marques and Nuno Baeta The indifference curve analysis - An alternative approach represented by ODEs using GeoGebra Representation by a marginal rate of substitution Definition (An indifference curve) An indifference curve is defined as the set of all bundles of goods which have the same preference rank (or utility level), that is, given a bundle P = (x0; y0), an indifference curve is the set 2 I = f(x; y) 2 R :(x; y) ∼ (x0; y0)g Definition (Marginal Rate of Substitution) 2 Let I be an indifference curve on R+. We say that τ is the marginal rate of substitution of Y for X if there exists a function of class C2 defined by y = f (x) such that dy = −τ(x; y) ; for all (x; y) 2 I : (1) dx Jorge Marques and Nuno Baeta The indifference curve analysis - An alternative approach represented by ODEs using GeoGebra Representation by a marginal rate of substitution Assumptions on Marginal Rate of Substitution In according to Hicks and Allen, it is assumed that: 1 2 (i*) Differentiability: τ is of class C on R+; 2 (ii*) Positivity: τ is positive on R+; @τ @τ (iii*) Convexity: − τ is negative on R2 . @x @y + The last assumption expresses expresses strict convexity of every indifference curve because the diminishing MRS principle states that the rate will decrease as Y good is substituted for X along an indifference curve. Jorge Marques and Nuno Baeta The indifference curve analysis - An alternative approach represented by ODEs using GeoGebra 2 Characterization of Preferences classes on R+ Geometric Interpretation 2 The consumer’s preferences on R+ are defined by giving for 2 each point P 2 R+ the direction orthogonal to an unknown indifference curve at P. Theorem If τ satisfies (i*), (ii*) and (iii*) then for every indifference curve there exists a function f defined by y = f (x) of class C2 satisfying (1) which is strictly decreasing and strictly convex. Jorge Marques and Nuno Baeta The indifference curve analysis - An alternative approach represented by ODEs using GeoGebra 2 Characterization of Preferences classes on R+ The Indifference Map It follows that the indifference map is the set of all curves such that: Each indifference curve is the graph of a function 2 f : D ⊂ R+ ! R, defined by y = f (x), of class C , positive, strictly decreasing and strictly convex; Indifference curves cannot intersect, that is, if c1 6= c2 we have Ic1 \ Ic2 = ;; The further the indifference curve from the origin, the higher the preference rank (or level of utility) c; A reunion of all indifference curves satisfies [ 2 Ic = R+: c>0 Jorge Marques and Nuno Baeta The indifference curve analysis - An alternative approach represented by ODEs using GeoGebra 2 Characterization of Preferences classes on R+ Definition (Linear Preferences) Two goods X1 and X2 are called perfect substitutes if marginal rates of substitution are positive constants for all bundles. Proposition (Representation Theorem) 2 Consumer’s preferences are linear on R+ if and only if the indifference map is represented by a family of lines of the equation y = −kx + c, where k > 0. Utility Representation Linear preferences are represented by any utility function U(x; y) = g(kx + y), where g is strictly increasing and k > 0. Jorge Marques and Nuno Baeta The indifference curve analysis - An alternative approach represented by ODEs using GeoGebra 2 Characterization of Preferences classes on R+ Definition (Quasi-Linear Preferences) Consumer’s preferences are said to be: (i) Quasi-linear with respect to X2 if there exists a positive and strictly decreasing function η on R+ such that 2 τ(x; y) = η(x) ; for all (x; y) 2 R+ ; (ii) Quasi-linear with respect to X1 if there exists a positive and strictly decreasing function φ on R+ such that 2 τ(x; y) = φ(y) ; for all (x; y) 2 R+ : Jorge Marques and Nuno Baeta The indifference curve analysis - An alternative approach represented by ODEs using GeoGebra 2 Characterization of Preferences classes on R+ Proposition (Representation Theorem) Consumer’s preferences are quasi-linear with respect to X2 on 2 R+ if and only if the indifference map is represented by a family of curves of equation y = c − F(x), where F is strictly increasing and strictly concave.
Load more

Recommended publications
  • Indifference Curves
    Lecture # 8 – Consumer Behavior: An Introduction to the Concept of Utility I. Utility -- A Description of Preferences • Our goal is to come up with a model that describes consumer behavior. To begin, we need a way to describe preferences. Economists use utility to do this. • Utility is the level of satisfaction that a person gets from consuming a good or undertaking an activity. o It is the relative ranking, not the actual number, that matters. • Marginal utility is the satisfaction obtained from consuming an additional amount of a good. It is the change in total utility resulting from a one-unit change in product. o Marginal utility diminishes (gets smaller) as you consume more of a good (the fifth ice cream cone isn't as desirable as the first). o However, as long as marginal utility is positive, total utility will increase! II. Mapping Preferences -- Indifference Curves • Since economics is about allocating scarce resources -- that is, asking what choices people make when faced with limited resources -- looking at utility for a single good is not enough. We want to compare utility for different combinations of two or more goods. • Our goal is to be able to graph the utility received from a combination of two goods with a two-dimensional diagram. We do this using indifference curves. • An indifference curve represents all combinations of goods that produce the same level of satisfaction to a person. o Along an indifference curve, utility is constant. o Remember that each curve is analogous to a line on a contour map, where each line shows a different elevation.
    [Show full text]
  • Chapter 4 4 Utility
    Chapter 4 Utility Preferences - A Reminder x y: x is preferred strictly to y. x y: x and y are equally preferred. x ~ y: x is preferred at least as much as is y. Preferences - A Reminder Completeness: For any two bundles x and y it is always possible to state either that xyx ~ y or that y ~ x. Preferences - A Reminder Reflexivity: Any bundle x is always at least as preferred as itself; iei.e. xxx ~ x. Preferences - A Reminder Transitivity: If x is at least as preferred as y, and y is at least as preferred as z, then x is at least as preferred as z; iei.e. x ~ y and y ~ z x ~ z. Utility Functions A preference relation that is complete, reflexive, transitive and continuous can be represented by a continuous utility function . Continuityyg means that small changes to a consumption bundle cause only small changes to the preference level. Utility Functions A utility function U(x) represents a preference relation ~ if and only if: x’ x” U(x’)>U(x) > U(x”) x’ x” U(x’) < U(x”) x’ x” U(x’) = U(x”). Utility Functions Utility is an ordinal (i.e. ordering) concept. E.g. if U(x) = 6 and U(y) = 2 then bdlibundle x is stri ilctly pref erred to bundle y. But x is not preferred three times as much as is y. Utility Functions & Indiff. Curves Consider the bundles (4,1), (2,3) and (2,2). Suppose (23)(2,3) (41)(4,1) (2, 2). Assiggyn to these bundles any numbers that preserve the preference ordering; e.g.
    [Show full text]
  • Mathematical Economics
    Mathematical Economics Dr Wioletta Nowak, room 205 C [email protected] http://prawo.uni.wroc.pl/user/12141/students-resources Syllabus Mathematical Theory of Demand Utility Maximization Problem Expenditure Minimization Problem Mathematical Theory of Production Profit Maximization Problem Cost Minimization Problem General Equilibrium Theory Neoclassical Growth Models Models of Endogenous Growth Theory Dynamic Optimization Syllabus Mathematical Theory of Demand • Budget Constraint • Consumer Preferences • Utility Function • Utility Maximization Problem • Optimal Choice • Properties of Demand Function • Indirect Utility Function and its Properties • Roy’s Identity Syllabus Mathematical Theory of Demand • Expenditure Minimization Problem • Expenditure Function and its Properties • Shephard's Lemma • Properties of Hicksian Demand Function • The Compensated Law of Demand • Relationship between Utility Maximization and Expenditure Minimization Problem Syllabus Mathematical Theory of Production • Production Functions and Their Properties • Perfectly Competitive Firms • Profit Function and Profit Maximization Problem • Properties of Input Demand and Output Supply Syllabus Mathematical Theory of Production • Cost Minimization Problem • Definition and Properties of Conditional Factor Demand and Cost Function • Profit Maximization with Cost Function • Long and Short Run Equilibrium • Total Costs, Average Costs, Marginal Costs, Long-run Costs, Short-run Costs, Cost Curves, Long-run and Short-run Cost Curves Syllabus Mathematical Theory of Production Monopoly Oligopoly • Cournot Equilibrium • Quantity Leadership – Slackelberg Model Syllabus General Equilibrium Theory • Exchange • Market Equilibrium Syllabus Neoclassical Growth Model • The Solow Growth Model • Introduction to Dynamic Optimization • The Ramsey-Cass-Koopmans Growth Model Models of Endogenous Growth Theory Convergence to the Balance Growth Path Recommended Reading • Chiang A.C., Wainwright K., Fundamental Methods of Mathematical Economics, McGraw-Hill/Irwin, Boston, Mass., (4th edition) 2005.
    [Show full text]
  • Behavioral Indifference Curves
    NBER WORKING PAPER SERIES BEHAVIORAL INDIFFERENCE CURVES John Komlos Working Paper 20240 http://www.nber.org/papers/w20240 NATIONAL BUREAU OF ECONOMIC RESEARCH 1050 Massachusetts Avenue Cambridge, MA 02138 June 2014 I would like to thank Jack Knetsch for comments on an earlier version of this paper. The views expressed herein are those of the author and do not necessarily reflect the views of the National Bureau of Economic Research. NBER working papers are circulated for discussion and comment purposes. They have not been peer- reviewed or been subject to the review by the NBER Board of Directors that accompanies official NBER publications. © 2014 by John Komlos. All rights reserved. Short sections of text, not to exceed two paragraphs, may be quoted without explicit permission provided that full credit, including © notice, is given to the source. Behavioral Indifference Curves John Komlos NBER Working Paper No. 20240 June 2014 JEL No. A2,D03,D11 ABSTRACT According to the endowment effect there is some discomfort associated with giving up a good, that is to say, we are willing to give up something only if the price is greater than the price we are willing to pay for it. This implies that the indifference curves should designate a reference point at the current level of consumption. Such indifference maps are kinked at the current level of consumption. The kinks in the curves imply that the utility function is not differentiable everywhere and the budget constraint does not always have a unique tangent with an indifference curve. Thus, price changes may not bring about changes in consumption which may be the reason for the frequent stickiness of prices, wages and interest rates.
    [Show full text]
  • Consumer Choice and Behavioral Economics
    CHAPTER 9| Consumer Choice and Behavioral Economics Chapter Summary and Learning Objectives 9.1 Utility and Consumer Decision Making (pages 280–288) Define utility and explain how consumers choose goods and services to maximize their utility. Utility is the enjoyment or satisfaction that people receive from consuming goods and services. The goal of a consumer is to spend available income so as to maximize utility. Marginal utility is the change in total utility a person receives from consuming one additional unit of a good or service. The law of diminishing marginal utility states that consumers receive diminishing additional satisfaction as they consume more of a good or service during a given period of time. The budget constraint is the amount of income consumers have available to spend on goods and services. To maximize utility, consumers should make sure they spend their income so that the last dollar spent on each product gives them the same marginal utility. The income effect is the change in the quantity demanded of a good that results from the effect of a change in the price on consumer purchasing power. The substitution effect is the change in the quantity demanded of a good that results from a change in price making the good more or less expensive relative to other goods, holding constant the effect of the price change on consumer purchasing power. 9.2 Where Demand Curves Come From (pages 288–291) Use the concept of utility to explain the law of demand. When the price of a good declines, the ratio of the marginal utility to price rises.
    [Show full text]
  • Locating the Consumer's Optimal Combination of Goods
    Locating the Consumer's Optimal Combination of Goods Review: The budget constraint shows the consumer’s opportunities for trade, or at what level the market is allowing him/her to trade. It shows the relative prices of the goods. Review: The consumer’s indifference curve map shows his/her willingness to trade. The consumer’s optimal combination of goods is at the point where the budget line is tangent to an indifference curve or where the marginal rate of substitution (MRS) is equal to the opportunity cost or relative price of the two goods, as indicated by the slope of the budget constraint. Review: The budget constraint gives the consumer’s opportunities for trade. It represents the possibilities open to the consumer. In the graph on the left, the slope Px/Py is the relative price of toys measured in terms of snacks. It tells us that if this consumer gives up one toy, he can get three snacks. This graph shows us the consumer’s optimal combination of snacks and toys. It is two toys and six snacks. You can determine this point by seeing that it is the one point shared by the budget constraint and the highest indifference curve that is tangent to the budget constraint. On the left, that indifference curve is U0. At the tangency point (2,6) the MRS (the slope of the indifference curve) is equal to the slope of the budget constraint. Consider a point at which the MRS<3, as on the left. At this point the consumer is willing to give up a toy for fewer than three snacks.
    [Show full text]
  • Preferences and Utility
    Preferences and Utility Simon Board¤ This Version: October 6, 2009 First Version: October, 2008. These lectures examine the preferences of a single agent. In Section 1 we analyse how the agent chooses among a number of competing alternatives, investigating when preferences can be represented by a utility function. In Section 2 we discuss two attractive properties of preferences: monotonicity and convexity. In Section 3 we analyse the agent's indi®erence curves and ask how she makes tradeo®s between di®erent goods. Finally, in Section 4 we look at some examples of preferences, applying the insights of the earlier theory. 1 The Foundation of Utility Functions 1.1 A Basic Representation Theorem Suppose an agent chooses from a set of goods X = fa; b; c; : : :g. For example, one can think of these goods as di®erent TV sets or cars. Given two goods, x and y, the agent weakly prefers x over y if x is at least as good as y. To avoid us having to write \weakly prefers" repeatedly, we simply write x < y. We now put some basic structure on the agent's preferences by adopting two axioms.1 Completeness Axiom: For every pair x; y 2 X, either x < y, y < x, or both. ¤Department of Economics, UCLA. http://www.econ.ucla.edu/sboard/. Please email suggestions and typos to [email protected]. 1An axiom is a foundational assumption. 1 Eco11, Fall 2009 Simon Board Transitivity Axiom: For every triple x; y; z 2 X, if x < y and y < z then x < z.
    [Show full text]
  • Vouchers, Equality and Competition
    Vouchers, equality and competition Martin Schonger A Dissertation Presented to the Faculty of Princeton University in Candidacy for the Degree of Doctor of Philosophy Recommended for Acceptance by the Department of Economics Adviser: Stephen Morris June 2012 c Copyright by Martin Schonger, 2012. All rights reserved. Abstract \Money follows people" is a policy instrument which in various incarnations can be used to publicly provide private goods such as health care and education. Fee-for-service (FFS) health care and school vouchers are examples. This dissertation is an applied theoretical investigation of that policy instrument and points out that it has two subtle and unintended consequences: categorical inequality and attenuation of competition. In my model each consumer purchases one unit of a discrete target good of variable quality. Government provides a fixed amount of money, a restricted transfer, which the consumer can spend only on the target good. By increasing the restricted transfer government can indirectly increase equilibrium quality even beyond what would occur under a cash transfer of the same size. If government employs this policy instrument to address a market imperfection (e.g. a positive externality of consumption) this distortion of individual consumption does not lead to the well-known deadweight loss of a restricted transfer that was first pointed out by Southworth (1945). But there are two other, problematic, consequences of the consumption distortion: First inequality in consumption of the target good arises even though all consumers spend the same. Second, the consumption distortion attenuates competition between producers. Inequality in consumption under restricted transfers is ironic: presumably this policy instrument is chosen in the first place to provide equal access irrespective of income.
    [Show full text]
  • Utility Function- That Will Be Useful to Solve the Equilibrium of the Consumer in Terms of Calculus
    Microeconomics I. Antonio Zabalza. University of Valencia 1 Micro I. Lesson 4. Utility In the previous lesson we have developed a method to rank consistently all bundles in the (x,y) space and we have introduced a concept –the indifference curve- to help us in this analysis. Now we introduce a related concept to rank bundles –the utility function- that will be useful to solve the equilibrium of the consumer in terms of calculus. 4.1 Ordinal versus cardinal utility In the past, utility was conceived as a quantitative measure of a person’s welfare out of consuming goods. Now it is recognised that utility cannot be quantified because of the impossibility of interpersonal comparisons. So we do now as we did in Lesson 3, we only rank bundles. Utility function: A way of assigning a number to every possible consumption bundle such that more- preferred bundles get assigned larger numbers than less-preferred bundles. (,x¢y¢)ff(x¢¢,y¢¢) if and only if Ux(¢,y¢)U(xy¢¢,)¢¢ The only property about the numbers the utility function generates which is important is how it orders the bundles; how it ranks them. The size of the difference between the numbers assigned to each Microeconomics I. Antonio Zabalza. University of Valencia 2 bundle does not matter. Thus we talk about ordinal utility. Since only the ranking matters, there can be no unique way to assign utility to bundles. If U(x,y) represents one way of ranking goods, 2U(x,y) is equally acceptable: it ranks bundles in the same manner. Multiplying by 2 is an example of a monotonic transformation.
    [Show full text]
  • Intermediate Microeconomics W3211 Lecture 2
    3/1/2016 1 Intermediate Microeconomics W3211 Lecture 2: Introduction Indifference Curves and Utility What do your preferences look like? Columbia University, Spring 2016 Mark Dean: [email protected] 2 3 4 The Story So Far…. Today’s Aims • In Monday’s lecture we described how we would model 1. Describe how to represent preferences on our handy graphs consumer choice as constrained optimization: Indifference Curves 1. CHOOSE a consumption bundle 2. Describe how to represent preferences using maths Utility functions 2. IN ORDER TO MAXIMIZE preferences 3. Describe ‘standard’ preferences 3. SUBJECT TO the budget constraint Monotonic Convex • Consumption bundles and budget constrains were dealt with fairly thoroughly 4. Introduce some other handy classes of preferences • Preferences may still seem a bit mysterious Perfect substitutes Perfect compliments • Today, we will attempt to de-mystify Cobb Douglas Reminder: Varian Ch. 3 & 4, Feldman and Serrano Ch 2 6 Going from Three Dimensions to Two • Think back to our nice, simple example with two goods • Made it nice and easy to graph the consumption bundles and budget constraints Indifference Curves Or: how to see your preferences 5 1 3/1/2016 7 8 Going from Three Dimensions to Two Going from Three Dimensions to Two • Think back to our nice, simple example with two goods • Unfortunately, we now have three pieces of information associated with each bundle • Made it nice and easy to graph the consumption bundles • Amount of good 1 and budget constraints • Amount of good 2 Budget constraint is • Whether this bundle is preferred or not to others m /p2 • How can we represent this information? p1x1 + p2x2 = m.
    [Show full text]
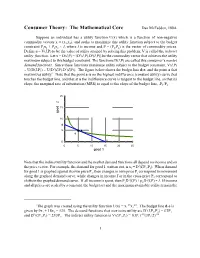
  • Consumer Theory: the Mathematical Core Dan Mcfadden, 100A
    Consumer Theory: The Mathematical Core Dan McFadden, 100A Suppose an individual has a utility function U(x) which is a function of non-negative commodity vectors x = (x1,x2), and seeks to maximize this utility function subject to the budget constraint P1x1 + P2x2 I, where I is income and P = (P1,P2) is the vector of commodity prices. Define u = V(I,P) to be the value of utility attained by solving this problem; V is called the indirect utility function. Let x = D(I,P) = (D1(I,P),D2(I,P)) be the commodity vector that achieves the utility maximum subject to this budget constraint. The functions D(I,P) are called this consumer’s market demand functions. Since these functions maximize utility subject to the budget constraint, V(I,P) U(D(I,P)) U(D1(I,P),D2(I,P)). The figure below shows the budget line d-e, and the point a that maximizes utility.1 Note that the point a is on the highest indifference (constant utility) curve that touches the budget line, and that at a the indifference curve is tangent to the budget line, so that its slope, the marginal rate of substitution (MRS) is equal to the slope of the budget line, -P1/P2. 20 15 10 d 5 a good 2 e 0 0 5 10 15 20 25 good 1 Note that the indirect utility function and the market demand functions all depend on income and on 1 the price vector. For example, the demand for good 1, written out, is x1 = D (I,P1,P2).
    [Show full text]
  • EC 203 - INTERMEDIATE MICROECONOMICS Bo˘Gazi¸Ciuniversity Department of Economics Fall 2019 Problem Set 1 - Solutions
    EC 203 - INTERMEDIATE MICROECONOMICS Bo˘gazi¸ciUniversity Department of Economics Fall 2019 Problem Set 1 - Solutions 1. Draw indifferences curves to represent each of the following type of preferences. (a) Quarters-dollars: A consumer is always happy to change 4 quarters for 1 dollar. Solution: quarters 8 4 dollars 1 2 (b) Bicycle frames-tires: A consumer always wants 2 tires to go with 1 frame. Solution: frames (y) 2y = x 2 2 bikes 1 1 bike tires (x) 2 4 2. Tom always begins his day with a strawberry milkshake. He makes it by mixing milk (x) with five strawberries (y). The secret of a really good milkshake lies in the optimal proportion of milk and fruit: one glass always comes with five strawberries. (a) Plot Tom's representative indifference curves. Depict three indifference curves that pass through the following bundles (5, 1), (10, 10) and (15, 4). What is the MRS at each of these points? Solution: See the graph below. MRS at each of these bundles is zero. (b) What utility function represents these preferences? On the graph from (a), indicate the level of utility corresponding to each indifference curve. Solution: A utility function that represents these preferences would be u(x; y) = minf5x; yg. The utility levels would be u(5; 1) = 1, u(10; 10) = 10, and u(15; 4) = 4 1 (c) Multiply your utility function by ten and add two to it. How did the indifference curves change? How was the level of utility associated with each indifference curve affected? Solution: We have, v(x; y) = 10 minf5x; yg + 2.
    [Show full text]