DOCSLIB.ORG

Wavelength: Λ (Lambda) Example: Wave on a String

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Wavelength: Λ (Lambda) Example: Wave on a String Review L 22 – Vibrations and Waves-3 •A mechanical wave is a disturbance that • resonance travels through a medium – solids, liquids or • clocks – pendulum gases – it is a vibration that propagates • springs • The disturbance moves because of the • harmonic motion elastic nature of the material • mechanical waves • sound waves • As the disturbance moves, the parts of the • The periodic wave relation material (segment of string, air molecules) • Wave interference execute harmonic motion (move up and – standing waves down or back and forth) – beats – transverse wave--- waves on strings • musical instruments – longitudinal wave --- sound 1 2 Wavelength: lambda) Period (T) or Frequency ( f ) Snapshot of the string at some time – freezes the motion Wave crests • An observer at a fixed position observes the wave moving by Time (s) • The time between Displacement (m) T T successive crests Wave troughs passing by (or troughs) is the PERIOD T • each segment of the string undergoes simple Period and frequency harmonic motion as the wave passes by are inversely related • The number of crests • distance between successive peaks (wave crests) 1 passing by per unit time is called the WAVELENGTH (lambda), it is T is the FREQUENCY f measured in meters or centimeters f 3 4 The periodic wave relation Example: wave on a string •The wavelength, period (or frequency) and wave speed are related •In one period the wave moves one 2 cm 2 cm 2 cm wavelength, so the wave speed v = /T •Since f = 1/T, this can be written as • A wave moves on a string at a speed of 4 cm/s f = v • A snapshot of the motion shows that the wavelength, = 2 cm, what is the frequency, ? which is the periodic wave relation. •v = , so = v / = (4 cm/s ) / (2 cm) = 2 Hz •T = 1 / f = 1 / (2 Hz) = 0.5 s 5 6 1 Making sound waves Tuning forks make sound waves longitudinal pressure disturbances • When the diaphragm in the speaker moves out it • The vibration of the fork causes the air near it to compresses the layer of vibrate air in front of it. • The length of the fork • This compressed air determines the frequency layer then expands and – longer fork lower f pushes on another layer – shorter fork higher f of air adjacent to it • It produces a pure pitch single frequency • A propagating sound wave is produced 7 8 Stringed instruments Bowed instruments • Three types – Plucked: guitar, bass, harp, harpsichord – Bowed: violin, viola, cello, bass – Struck: piano • In violins, violas, cellos and basses, a bow made of horse hair • All use strings that are fixed at both ends is used to excite the strings into vibration • The speed of the wave on the string depends on: • Each of these instruments are successively bigger (longer and – The tension in the string which is adjustable (tuning) heavier strings). – The thickness of the string (instruments have some • The shorter strings make the high frequencies and the long thin and some thicker strings) strings make the low frequencies • The periodic wave relation applies: f = v • Bowing excites many vibration modes simultaneously includes a mixture of tones (richness) 9 10 Wind instruments: organs, flutes… St. Vincent’s Episcopal Church in Bedford, Texas Gravissima 8.2 Hz • The air pressure inside the pipe can vibrate, in some 4400 Hz places it is high and in other places low • Depending on the length of the pipe, various resonant modes are excited, just like blowing across a pop bottle • The long pipes make the low notes, the short pipes make the high notes 11 12 2 Constructive Destructive Wave interference Interference Interference • If there are 2 waves on a string, they can A A combine together to make another type of wave called a standing wave • Standing waves are produced by an effect called wave interference, and there are two B B types of interference: – Constructive interference – the combination wave is bigger than the 2 waves – Destructive interference- the combination wave is smaller than the 2 waves A+B A+B 13 14 Wave interference effects Standing waves • standing waves are produced by wave interference • when a transverse wave is launched on a string, a • Waves can interfere with each other in reflected wave is produced at the other end space or in time • Wave interference in space gives rise to standing waves • Wave interference in time gives rise to beats • the primary and reflected waves interfere with each other to produce a standing wave • In some places along the string, the waves interfere 15 constructively and at other places destructively 16 Modes of vibration Standing waves • Nodes N the string does not move • Antinodes A string has maximum amplitude • At the NODES, the string does not move NNFundamental mode • At the ANTINODES the string moves up A Wavelength = 2 L and down harmonically Frequency = f L o • Since the ends are fixed, only an integer N N First harmonic mode number of half wavelengths can fit A N A Wavelength = L • e. g., 2 L, L, 2/3 L, ½ L, etc. Frequency = 2 fo • The frequency is determined by the N N Second harmonic mode velocity and mode number (wavelength) A Wavelength = 2/3 L N A N A Frequency = 3 fo 17 18 3 Mode vibration frequencies Beats – sound wave interference • In general, f = v / , where v is the Beats occur when 2 waves of slightly propagation speed of the string different frequencies are combined. • The propagation speed depends on the diameter and tension of the string • Modes – Fundamental: fo = v / 2L – First harmonic: f1 = v / L = 2 fo – Second harmonic: f2 = v / (2/3)L = 3 fo • The effective length can be changed by the musician “fingering” the strings 19 20 Wave interference can be used to eliminate Room acoustics noise – anti-noise technology • Destructive interference accounts for bad Noise elimination headphones room acoustics The noise wave is inverted and added to the original • Sound that bounces off a wall can interfere wave, so the noise is effectively cancelled out. destructively (cancel out) sound from the speakers resulting in dead spots + 21 22 4.
Load more

Recommended publications
  • Glossary Physics (I-Introduction)
    1 Glossary Physics (I-introduction) - Efficiency: The percent of the work put into a machine that is converted into useful work output; = work done / energy used [-]. = eta In machines: The work output of any machine cannot exceed the work input (<=100%); in an ideal machine, where no energy is transformed into heat: work(input) = work(output), =100%. Energy: The property of a system that enables it to do work. Conservation o. E.: Energy cannot be created or destroyed; it may be transformed from one form into another, but the total amount of energy never changes. Equilibrium: The state of an object when not acted upon by a net force or net torque; an object in equilibrium may be at rest or moving at uniform velocity - not accelerating. Mechanical E.: The state of an object or system of objects for which any impressed forces cancels to zero and no acceleration occurs. Dynamic E.: Object is moving without experiencing acceleration. Static E.: Object is at rest.F Force: The influence that can cause an object to be accelerated or retarded; is always in the direction of the net force, hence a vector quantity; the four elementary forces are: Electromagnetic F.: Is an attraction or repulsion G, gravit. const.6.672E-11[Nm2/kg2] between electric charges: d, distance [m] 2 2 2 2 F = 1/(40) (q1q2/d ) [(CC/m )(Nm /C )] = [N] m,M, mass [kg] Gravitational F.: Is a mutual attraction between all masses: q, charge [As] [C] 2 2 2 2 F = GmM/d [Nm /kg kg 1/m ] = [N] 0, dielectric constant Strong F.: (nuclear force) Acts within the nuclei of atoms: 8.854E-12 [C2/Nm2] [F/m] 2 2 2 2 2 F = 1/(40) (e /d ) [(CC/m )(Nm /C )] = [N] , 3.14 [-] Weak F.: Manifests itself in special reactions among elementary e, 1.60210 E-19 [As] [C] particles, such as the reaction that occur in radioactive decay.
    [Show full text]
  • The Science of String Instruments
    The Science of String Instruments Thomas D. Rossing Editor The Science of String Instruments Editor Thomas D. Rossing Stanford University Center for Computer Research in Music and Acoustics (CCRMA) Stanford, CA 94302-8180, USA [email protected] ISBN 978-1-4419-7109-8 e-ISBN 978-1-4419-7110-4 DOI 10.1007/978-1-4419-7110-4 Springer New York Dordrecht Heidelberg London # Springer Science+Business Media, LLC 2010 All rights reserved. This work may not be translated or copied in whole or in part without the written permission of the publisher (Springer Science+Business Media, LLC, 233 Spring Street, New York, NY 10013, USA), except for brief excerpts in connection with reviews or scholarly analysis. Use in connection with any form of information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed is forbidden. The use in this publication of trade names, trademarks, service marks, and similar terms, even if they are not identified as such, is not to be taken as an expression of opinion as to whether or not they are subject to proprietary rights. Printed on acid-free paper Springer is part of Springer ScienceþBusiness Media (www.springer.com) Contents 1 Introduction............................................................... 1 Thomas D. Rossing 2 Plucked Strings ........................................................... 11 Thomas D. Rossing 3 Guitars and Lutes ........................................................ 19 Thomas D. Rossing and Graham Caldersmith 4 Portuguese Guitar ........................................................ 47 Octavio Inacio 5 Banjo ...................................................................... 59 James Rae 6 Mandolin Family Instruments........................................... 77 David J. Cohen and Thomas D. Rossing 7 Psalteries and Zithers .................................................... 99 Andres Peekna and Thomas D.
    [Show full text]
  • Test of Self-Organization in Beach Cusp Formation Giovanni Coco,1 T
    JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 108, NO. C3, 3101, doi:10.1029/2002JC001496, 2003 Test of self-organization in beach cusp formation Giovanni Coco,1 T. K. Burnet, and B. T. Werner Complex Systems Laboratory, Cecil and Ida Green Institute of Geophysics and Planetary Physics, University of California, San Diego, La Jolla, California, USA Steve Elgar Woods Hole Oceanographic Institution, Woods Hole, Massachusetts, USA Received 4 June 2002; revised 6 November 2002; accepted 13 November 2002; published 29 March 2003. [1] Field observations of swash flow patterns and morphology change are consistent with the hypothesis that beach cusps form by self-organization, wherein positive feedback between swash flow and developing morphology causes initial development of the pattern and negative feedback owing to circulation of flow within beach cusp bays causes pattern stabilization. The self-organization hypothesis is tested using measurements from three experiments on a barrier island beach in North Carolina. Beach cusps developed after the beach was smoothed by a storm and after existing beach cusps were smoothed by a bulldozer. Swash front motions were recorded on video during daylight hours, and morphology was measured by surveying at 3–4 hour intervals. Three signatures of self- organization were observed in all experiments. First, time lags between swash front motions in beach cusp bays and horns increase with increasing relief, representing the effect of morphology on flow. Second, differential erosion between bays and horns initially increases with increasing time lag, representing the effect of flow on morphology change because positive feedback causes growth of beach cusps. Third, after initial growth, differential erosion decreases with increasing time lag, representing the onset of negative feedback that stabilizes beach cusps.
    [Show full text]
  • Standing Waves and Sound
    Standing Waves and Sound Waves are vibrations (jiggles) that move through a material Frequency: how often a piece of material in the wave moves back and forth. Waves can be longitudinal (back-and- forth motion) or transverse (up-and- down motion). When a wave is caught in between walls, it will bounce back and forth to create a standing wave, but only if its frequency is just right! Sound is a longitudinal wave that moves through air and other materials. In a sound wave the molecules jiggle back and forth, getting closer together and further apart. Work with a partner! Take turns being the “wall” (hold end steady) and the slinky mover. Making Waves with a Slinky 1. Each of you should hold one end of the slinky. Stand far enough apart that the slinky is stretched. 2. Try making a transverse wave pulse by having one partner move a slinky end up and down while the other holds their end fixed. What happens to the wave pulse when it reaches the fixed end of the slinky? Does it return upside down or the same way up? Try moving the end up and down faster: Does the wave pulse get narrower or wider? Does the wave pulse reach the other partner noticeably faster? 3. Without moving further apart, pull the slinky tighter, so it is more stretched (scrunch up some of the slinky in your hand). Make a transverse wave pulse again. Does the wave pulse reach the end faster or slower if the slinky is more stretched? 4. Try making a longitudinal wave pulse by folding some of the slinky into your hand and then letting go.
    [Show full text]
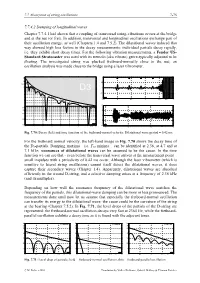
  • 7.7.4.2 Damping of Longitudinal Waves Chapter 7.7.4.1 Had Shown That a Coupling of Transversal String-Vibrations Occurs at the Bridge and at the Nut (Or Fret)
    7.7 Absorption of string oscillations 7-75 7.7.4.2 Damping of longitudinal waves Chapter 7.7.4.1 had shown that a coupling of transversal string-vibrations occurs at the bridge and at the nut (or fret). In addition, transversal and longitudinal oscillations exchange part of their oscillation energy, as well (Chapters 1.4 and 7.5.2). The dilatational waves induced that way showed high loss factors in the decay measurements: individual partials decay rapidly, i.e. they exhibit short decay times. For the following vibration measurements, a Fender US- Standard Stratocaster was used with its tremolo (aka vibrato) genre-typically adjusted to be floating. The investigated string was plucked fretboard-normally close to the nut; an oscillation analysis was made close to the bridge using a laser vibrometer. Fig. 7.70: Decay (left) and time function of the fretboard-normal velocity. Dilatational wave period = 0.42 ms. For the fretboard normal velocity, the left-hand image in Fig. 7.70 shows the decay time of the D3-partials. Damping maxima – i.e. T30 minima – can be identified at 2.36, at 4.7 and at 7.1 kHz; resonances of dilatational waves can be assumed to be the cause. In the time function we can see that - even before the transversal wave arrives at the measurement point – small impulses with a periodicity of 0.42 ms occur. Although the laser vibrometer (which is sensitive to lateral string oscillations) cannot itself detect the dilatational waves, it does capture their secondary waves (Chapter 1.4). Apparently, dilatational waves are absorbed efficiently in the wound D-string, and a selective damping arises at a frequency of 2.36 kHz (and its multiples).
    [Show full text]
  • Chapter 16: Fourier Series
    Chapter 16: Fourier Series 16.1 Fourier Series Analysis: An Overview A periodic function can be represented by an infinite sum of sine and cosine functions that are harmonically related: Ϧ ͚ʚͨʛ Ɣ ͕1 ƍ ȕ ͕) cos ͢!*ͨ ƍ ͖) sin ͢!*ͨ Fourier Coefficients: are)Ͱͥ calculated from ͕1; ͕); ͖) ͚ʚͨʛ Fundamental Frequency: ͦ_ where multiples of this frequency are called !* Ɣ ; ͢! * harmonic frequencies Conditions that ensure that f(t) can be expressed as a convergent Fourier series: (Dirichlet’s conditions) 1. f(t) be single-values 2. f(t) have a finite number of discontinuities in the periodic interval 3. f(t) have a finite number of maxima and minima in the periodic interval 4. the integral /tͮ exists Ȅ/ |͚ʚͨʛ|ͨ͘; t These are sufficient conditions not necessary conditions; therefore if these conditions exist the functions can be expressed as a Fourier series. However if the conditions are not met the function may still be expressible as a Fourier series. 16.2 The Fourier Coefficients Defining the Fourier coefficients: /tͮ 1 ͕1 Ɣ ǹ ͚ʚͨʛͨ͘ ͎ /t /tͮ 2 ͕& Ɣ ǹ ͚ʚͨʛ cos ͟!*ͨ ͨ͘ ͎ /t /tͮ 2 ͖& Ɣ ǹ ͚ʚͨʛ sin ͟!*ͨ ͨ͘ ͎ / t Example 16.1 Find the Fourier series for the periodic waveform shown. Assessment problems 16.1 & 16.2 ECEN 2633 Spring 2011 Page 1 of 5 16.3 The Effects of Symmetry on the Fourier Coefficients Four types of symmetry used to simplify Fourier analysis 1. Even-function symmetry 2. Odd-function symmetry 3.
    [Show full text]
  • Giant Slinky: Quantitative Exhibit Activity
    Name: _________________________________________________________________ Giant Slinky: Quantitative Exhibit Activity Materials: Tape Measure, Stopwatch, & Calculator. In this activity, we will explore wave properties using the Giant Slinky. Let’s start by describing the two types of waves: transverse and longitudinal. Transverse and Longitudinal Waves A transverse wave moves side-to-side orthogonal (at a right angle; perpendicular) to the direction the wave is moving. These waves can be created on the Slinky by shaking the end of it left and right. A longitudinal wave is a pressure wave alternating between high and low pressure. These waves can be created on the Slinky by gathering a few (about 5 or so) Slinky rings, compressing them with your hands and letting go. The area of high pressure is where the Slinky rings are bunched up and the area of low pressure is where the Slinky rings are spread apart. Transverse Waves Before we can do any math with our Slinky, we need to know a little more about its properties. Begin by measuring the length (L) of the Slinky (attachment disk to attachment disk). If your tape measure only measures in feet and inches, convert feet into meters using 1 ft = 0.3048 m. Length of Slinky: L = __________________m We must also know how long it takes a wave to travel the length of the Slinky so that we can calculate the speed of a wave. For now, we are going to investigate transverse waves, so make a single pulse by jerking the Slinky sharply to the left and right ONCE (very quickly) and then return the Slinky to the original center position.
    [Show full text]
  • Estimating Fire Properties by Remote Sensing
    Estimating Fire Properties by Remote Sensing1. Philip J. Riggan USDA Forest Service Pacific Southwest Research Station 4955 Canyon Crest Drive Riverside, CA 92507 909 680 1534 [email protected] James W. Hoffman Space Instruments, Inc. 4403 Manchester Avenue, Suite 203 Encinitas, CA 92024 760 944 7001 [email protected] James A. Brass NASA Ames Research Center Moffett Federal Airfield, CA 94035 650 604 5232 [email protected] Abstract---Contemporary knowledge of the role of fire in the TABLE OF CONTENTS global environment is limited by inadequate measurements of the extent and impact of individual fires. Observations by 1. INTRODUCTION operational polar-orbiting and geostationary satellites provide an 2. ESTIMATING FIRE PROPERTIES indication of fire occurrence but are ill-suited for estimating the 3. ESTIMATES FROM TWO CHANNELS temperature, area, or radiant emissions of active wildland and 4. MULTI-SPECTRAL FIRE IMAGING agricultural fires. Simulations here of synthetic remote sensing 5. APPLICATIONS FOR FIRE MONITORING pixels comprised of observed high resolution fire data together with ash or vegetation background demonstrate that fire properties including flame temperature, fractional area, and INTRODUCTION radiant-energy flux can best be estimated from concurrent radiance measurements at wavelengths near 1.6, 3.9, and 12 µm, More than 30,000 fire observations were recorded over central Successful observations at night may be made at scales to at Brazil during August 1999 by Advanced Very High Resolution least I km for the cluster of fire data simulated here. During the Radiometers operating aboard polarorbiting satellites of the U.S. daytime, uncertainty in the composition of the background and National Oceanic and Atmospheric Administration.
    [Show full text]
  • Coating Provides Infrared Camouflage
    COURTESY OF PATRICK RONEY, ALIREZA SHAHSAFI AND MIKHAIL KATS February 1, 2020 Coating Provides Infrared Camouflage February 1, 2020 Coating Provides Infrared Camouflage About this Guide This Guide, based on the Science News article “Coating provides infrared camouflage,” asks students to explore the physics and potential technological applications of a material, discuss the various types of electromagnetic radiation, analyze infrared images and research how infrared imaging is used across a range of fields. This Guide includes: Article-based Comprehension Q&A — These questions, based on the Science News article “Coating provides infrared camouflage,” Readability: 12.7, ask students to explore the physics and potential technological applications of a material. Related standards include NGSS-DCI: HS-PS4; HS-PS3; HS-PS2; HS-ETS1. Student Comprehension Worksheet — These questions are formatted so it’s easy to print them out as a worksheet. Cross-curricular Discussion Q&A — Students will watch a NASA video about the electromagnetic spectrum to learn about properties of the various types of radiation. Then, students will explore and discuss technologies that use specific types of electromagnetic radiation. Related standards include NGSS- DCI: HS-PS4; HS-PS3; HS-PS2. Student Discussion Worksheet — These questions are formatted so it’s easy to print them out as a worksheet. Activity: Seeing in Infrared Summary: In this activity, students will analyze infrared images and then explore how infrared imaging is used across a range of fields of work. Skills include researching, evaluating, synthesizing and presenting information. Related standards include NGSS-DCI: HS-PS4; HS-PS3; HS-ETS1. Approximate class time: 1 class period to complete the discussion, research, presentations and debriefing as a class.
    [Show full text]
  • Sound and Vision: Visualization of Music with a Soap Film, and the Physics Behind It C Gaulon, C Derec, T Combriat, P Marmottant, F Elias
    Sound and Vision: Visualization of music with a soap film, and the physics behind it C Gaulon, C Derec, T Combriat, P Marmottant, F Elias To cite this version: C Gaulon, C Derec, T Combriat, P Marmottant, F Elias. Sound and Vision: Visualization of music with a soap film, and the physics behind it. 2017. hal-01487166 HAL Id: hal-01487166 https://hal.archives-ouvertes.fr/hal-01487166 Preprint submitted on 11 Mar 2017 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Sound and Vision: Visualization of music with a soap film, and the physics behind it C. Gaulon1, C. Derec1, T. Combriat2, P. Marmottant2 and F. Elias1;3 1 Laboratoire Mati`ere et Syst`emesComplexes UMR 7057, Universit´eParis Diderot, Sorbonne Paris Cit´e,CNRS, F-75205 Paris, France 2 Laboratoire Interdisciplinaire de Physique LIPhy, Universit´eGrenoble Alpes and CNRS UMR 5588 3 Sorbonne Universit´es,UPMC Univ Paris 06, 4 place Jussieu, 75252 PARIS cedex 05, France fl[email protected] Abstract A vertical soap film, freely suspended at the end of a tube, is vi- brated by a sound wave that propagates in the tube.
    [Show full text]
  • Woods for Wooden Musical Instruments S
    ISMA 2014, Le Mans, France Woods for Wooden Musical Instruments S. Yoshikawaa and C. Walthamb aKyushu University, Graduate School of Design, 4-9-1 Shiobaru, Minami-ku, 815-8540 Fukuoka, Japan bUniversity of British Columbia, Dept of Physics & Astronomy, 6224 Agricultural Road, Vancouver, BC, Canada V6T 1Z1 [email protected] 281 ISMA 2014, Le Mans, France In spite of recent advances in materials science, wood remains the preferred construction material for musical instruments worldwide. Some distinguishing features of woods (light weight, intermediate quality factor, etc.) are easily noticed if we compare material properties between woods, a plastic (acrylic), and a metal (aluminum). Woods common in musical instruments (strings, woodwinds, and percussions) are typically (with notable exceptions) softwoods (e.g. Sitka spruce) as tone woods for soundboards, hardwoods (e.g. amboyna) as frame woods for backboards, and monocots (e.g. bamboo) as bore woods for woodwind bodies. Moreover, if we consider the radiation characteristics of tap tones from sample plates of Sitka spruce, maple, and aluminum, a large difference is observed above around 2 kHz that is attributed to the relative strength of shear and bending deformations in flexural vibrations. This shear effect causes an appreciable increase in the loss factor at higher frequencies. The stronger shear effect in Sitka spruce than in maple and aluminum seems to be relevant to soundboards because its low-pass filter effect with a cutoff frequency of about 2 kHz tends to lend the radiated sound a desired softness. A classification diagram of traditional woods based on an anti-vibration parameter (density ρ/sound speed c) and transmission parameter cQ is proposed.
    [Show full text]
  • The Electromagnetic Spectrum
    The Electromagnetic Spectrum Wavelength/frequency/energy MAP TAP 2003-2004 The Electromagnetic Spectrum 1 Teacher Page • Content: Physical Science—The Electromagnetic Spectrum • Grade Level: High School • Creator: Dorothy Walk • Curriculum Objectives: SC 1; Intro Phys/Chem IV.A (waves) MAP TAP 2003-2004 The Electromagnetic Spectrum 2 MAP TAP 2003-2004 The Electromagnetic Spectrum 3 What is it? • The electromagnetic spectrum is the complete spectrum or continuum of light including radio waves, infrared, visible light, ultraviolet light, X- rays and gamma rays • An electromagnetic wave consists of electric and magnetic fields which vibrates thus making waves. MAP TAP 2003-2004 The Electromagnetic Spectrum 4 Waves • Properties of waves include speed, frequency and wavelength • Speed (s), frequency (f) and wavelength (l) are related in the formula l x f = s • All light travels at a speed of 3 s 108 m/s in a vacuum MAP TAP 2003-2004 The Electromagnetic Spectrum 5 Wavelength, Frequency and Energy • Since all light travels at the same speed, wavelength and frequency have an indirect relationship. • Light with a short wavelength will have a high frequency and light with a long wavelength will have a low frequency. • Light with short wavelengths has high energy and long wavelength has low energy MAP TAP 2003-2004 The Electromagnetic Spectrum 6 MAP TAP 2003-2004 The Electromagnetic Spectrum 7 Radio waves • Low energy waves with long wavelengths • Includes FM, AM, radar and TV waves • Wavelengths of 10-1m and longer • Low frequency • Used in many
    [Show full text]