An Overview of Spatial Microscopic and Accelerated Kinetic Monte Carlo Methods
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Wu Washington 0250E 15755.Pdf (3.086Mb)
© Copyright 2016 Sang Wu Contributions to Physics-Based Aeroservoelastic Uncertainty Analysis Sang Wu A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy University of Washington 2016 Reading Committee: Eli Livne, Chair Mehran Mesbahi Dorothy Reed Frode Engelsen Program Authorized to Offer Degree: Aeronautics and Astronautics University of Washington Abstract Contributions to Physics-Based Aeroservoelastic Uncertainty Analysis Sang Wu Chair of the Supervisory Committee: Professor Eli Livne The William E. Boeing Department of Aeronautics and Astronautics The thesis presents the development of a new fully-integrated, MATLAB based simulation capability for aeroservoelastic (ASE) uncertainty analysis that accounts for uncertainties in all disciplines as well as discipline interactions. This new capability allows probabilistic studies of complex configuration at a scope and with depth not known before. Several statistical tools and methods have been integrated into the capability to guide the tasks such as parameter prioritization, uncertainty reduction, and risk mitigation. The first task of the thesis focuses on aeroservoelastic uncertainty assessment considering control component uncertainty. The simulation has shown that attention has to be paid, if notch filters are used in the aeroservoelastic loop, to the variability and uncertainties of the aircraft involved. The second task introduces two innovative methodologies to characterize the unsteady aerodynamic uncertainty. One is a physically based aerodynamic influence coefficients element by element correction uncertainty scheme and the other is an alternative approach focusing on rational function approximation matrix uncertainties to evaluate the relative impact of uncertainty in aerodynamic stiffness, damping, inertia, or lag terms. Finally, the capability has been applied to obtain the gust load response statistics accounting for uncertainties in both aircraft and gust profiles. -

Anion Vacancies As a Source of Persistent Photoconductivity in II-VI and Chalcopyrite Semiconductors
PHYSICAL REVIEW B 72, 035215 ͑2005͒ Anion vacancies as a source of persistent photoconductivity in II-VI and chalcopyrite semiconductors Stephan Lany and Alex Zunger National Renewable Energy Laboratory, Golden, Colorado 80401, USA ͑Received 13 January 2005; revised manuscript received 12 April 2005; published 18 July 2005͒ Using first-principles electronic structure calculations we identify the anion vacancies in II-VI and chalcopy- rite Cu-III-VI2 semiconductors as a class of intrinsic defects that can exhibit metastable behavior. Specifically, ͑ ͒ we predict persistent electron photoconductivity n-type PPC caused by the oxygen vacancy VO in n-ZnO, originating from a metastable shallow donor state of VO. In contrast, we predict persistent hole photoconduc- ͑ ͒ tivity p-type PPC caused by the Se vacancy VSe in p-CuInSe2 and p-CuGaSe2. We find that VSe in the chalcopyrite materials is amphoteric having two “negative-U”-like transitions, i.e., a double-donor transition ͑2+/0͒ close to the valence band and a double-acceptor transition ͑0/2−͒ closer to the conduction band. We introduce a classification scheme that distinguishes two types of defects: type ␣, which have a defect-localized- state ͑DLS͒ in the band gap, and type , which have a resonant DLS within the host bands ͑e.g., the conduction band for donors͒. In the latter case, the introduced carriers ͑e.g., electrons͒ relax to the band edge where they can occupy a perturbed-host state. Type ␣ is nonconducting, whereas type  is conducting. We identify the neutral anion vacancy as type ␣ and the doubly positively charged vacancy as type . -

Analysing Census at School Data
Analysing Census At School Data www.censusatschool.ie Project Maths Development Team 2015 Page 1 of 7 Excel for Analysing Census At School Data Having retrieved a class’s data using CensusAtSchool: 1. Save the downloaded class data which is a .csv file as an .xls file. 2. Delete any unwanted variables such as the teacher name, date stamp etc. 3. Freeze the top row so that one can scroll down to view all of the data while the top row remains in view. 4. Select certain columns (not necessarily contiguous) for use as a class worksheet. Aim to have a selection of categorical data (nominal and ordered) and numerical data (discrete and continuous) unless one requires one type exclusively. The number of columns will depend on the class as too much data might be intimidating for less experienced classes. Students will need to have the questionnaire to hand to identify the question which produced the data. 5. Make a new worksheet within the workbook of downloaded data using the selected columns. 6. Name the worksheet i.e. “data for year 2 2014” or “data for margin of error investigation”. 7. Format the data to show all borders (useful if one is going to make a selection of the data and put it into Word). 8. Order selected columns of this data perhaps (and use expand selection) so that rogue data such as 0 for height etc. can be eliminated. It is perhaps useful for students to see this. (Use Sort & Filter.) 9. Use a filter on data, for example based on gender, to generate further worksheets for future use 10. -

A Monte Carlo Simulation Approach to the Reliability Modeling of the Beam Permit System of Relativistic Heavy Ion Collider (Rhic) at Bnl* P
Proceedings of ICALEPCS2013, San Francisco, CA, USA MOPPC075 A MONTE CARLO SIMULATION APPROACH TO THE RELIABILITY MODELING OF THE BEAM PERMIT SYSTEM OF RELATIVISTIC HEAVY ION COLLIDER (RHIC) AT BNL* P. Chitnis#, T.G. Robertazzi, Stony Brook University, Stony Brook, NY 11790, U.S.A. K.A. Brown, Brookhaven National Laboratory, Upton, NY 11973, U.S.A. Abstract called the Permit Carrier Link, Blue Carrier Link and The RHIC Beam Permit System (BPS) monitors the Yellow Carrier link. These links carry 10 MHz signals health of RHIC subsystems and takes active decisions whose presence allows the beam in the ring. Support regarding beam-abort and magnet power dump, upon a systems report their status to BPS through “Input subsystem fault. The reliability of BPS directly impacts triggers” called Permit Inputs (PI) and Quench Inputs the RHIC downtime, and hence its availability. This work (QI). If any support system PI fails, the permit carrier assesses the probability of BPS failures that could lead to terminates, initiating a beam dump. If QI fails, then the substantial downtime. A fail-safe condition imparts blue and yellow carriers also terminate, initiating magnet downtime to restart the machine, while a failure to power dump in blue and yellow ring magnets. The carrier respond to an actual fault can cause potential machine failure propagates around the ring to inform other PMs damage and impose significant downtime. This paper about the occurrence of a fault. illustrates a modular multistate reliability model of the Other than PMs, BPS also has 4 Abort Kicker Modules BPS, with modules having exponential lifetime (AKM) that see the permit carrier failure and send the distributions. -

Study on Vacancy Defect Concentration and Hybrid Potential of Metal-Based Epitaxial Graphene with Temperature
Study on Vacancy Defect Concentration and Hybrid Potential of Metal-based Epitaxial Graphene with Temperature J H Gao, W Liu*, X X Ren and R L Zheng Engineering Research Center of New Energy Storage Devices and Applications, Chongqing Chongqing University of Arts and Sciences, Chongqing 402160, P. R.China Corresponding author and e-mail: W Liu, [email protected] Abstract. This paper investigates the variation of the vacancy defect concentration and hybrid potential of copper and nickel - based epitaxial graphene with temperature by considering the existence of vacancy defects. Moreover, we discuss the impact of atomic non - harmonic vibration on the metal - based epitaxial graphene. First, the concentration of vacancy defects increases nonlinearly with increasing temperature, and the changing rate of the vacancy defect concentration of the metal-based epitaxial graphene with temperature is smaller than that of graphene; Second, the hybrid potential increases with increasing temperature, but not much; Third, the hybrid potential is independent of temperature without considering the atomic non-harmonic vibration which has an important influence on the vacancy defect concentration and the hybrid potential. The higher the temperature is, the more significant the non-harmonic effects are. 1. Introduction Epitaxial graphene has attracted the attention of researchers worldwide for its application prospect [1-4]. Conductivity is one of the most widely used and most important properties. Beside the experimental research, many literatures have studied the conductivity of epitaxial graphene. In 2013, Z Z Alisultanov studied the electrical conductivity of electron gas on metal-based and semiconductor-based epitaxial graphene in Ref. [5]. In 2015, the variation of electrical conductivity with temperature and thickness of little layer graphene and graphene nanosheets were studied, indicating that the electrical conductivity gradually decreased with increasing temperature in Ref. -
2 3 Practice Problems.Pdf
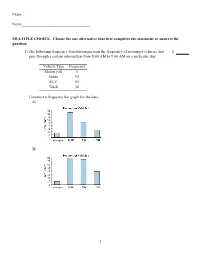
Exam Name___________________________________ MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. 1) The following frequency distribution presents the frequency of passenger vehicles that 1) pass through a certain intersection from 8:00 AM to 9:00 AM on a particular day. Vehicle Type Frequency Motorcycle 5 Sedan 95 SUV 65 Truck 30 Construct a frequency bar graph for the data. A) B) 1 C) D) 2) The following bar graph presents the average amount a certain family spent, in dollars, on 2) various food categories in a recent year. On which food category was the most money spent? A) Dairy products B) Cereals and baked goods C) Fruits and vegetables D) Meat poultry, fish, eggs 3) The following frequency distribution presents the frequency of passenger vehicles that 3) pass through a certain intersection from 8:00 AM to 9:00 AM on a particular day. Vehicle Type Frequency Motorcycle 9 Sedan 54 SUV 27 2 Truck 53 Construct a relative frequency bar graph for the data. A) B) C) D) 3 4) The following frequency distribution presents the frequency of passenger vehicles that 4) pass through a certain intersection from 8:00 AM to 9:00 AM on a particular day. Vehicle Type Frequency Motorcycle 9 Sedan 20 SUV 25 Truck 39 Construct a pie chart for the data. A) B) C) D) 5) The following pie chart presents the percentages of fish caught in each of four ratings 5) categories. Match this pie chart with its corresponding Parato chart. 4 A) B) C) 5 D) SHORT ANSWER. -

Type Here Title of the Paper
ICME 11, TSG 13, Monterrey, Mexico, 2008: Dave Pratt Shaping the Experience of Young and Naïve Probabilists Pratt, Dave Institute of Education, University of London. [email protected] Summary This paper starts by briefly summarizing research which has focused on student misconceptions with respect to understanding probability, before outlining the author’s research, which, in contrast, presents what students of age 11-12 years(Grade 7) do know and can construct, given access to a carefully designed environment. These students judged randomness according to unpredictability, lack of pattern in results, lack of control over outcomes and fairness. In many respects their judgments were based on similar characteristics to those of experts. However, it was only through interaction with a virtual environment, ChanceMaker, that the students began to express situated meanings for aggregated long-term randomness. That data is then re-analyzed in order to reflect upon the design decisions that shaped the environment itself. Four main design heuristics are identified and elaborated: Testing personal conjectures, Building on student knowledge, Linking purpose and utility, Fusing control and representation. In conclusion, it is conjectured that these heuristics are of wider relevance to teachers and lecturers, who aspire to shape the experience of young and naïve probabilists through their actions as designers of tasks and pedagogical settings. Preamble The aim in this paper is to propose heuristics that might usefully guide design decisions for pedagogues, who might be building software, creating new curriculum approaches, imagining a novel task or writing a lesson plan. (Here I use the term “heuristics” with its standard meaning as a rule-of-thumb, a guiding rule, rather than in the specialized sense that has been adopted by researchers of judgments of chance.) With this aim in mind, I re-analyze data that have previously informed my research on students’ meanings for randomness as emergent during activity. -

Revisiting the Sustainable Happiness Model and Pie Chart: Can Happiness Be Successfully Pursued?
The Journal of Positive Psychology Dedicated to furthering research and promoting good practice ISSN: 1743-9760 (Print) 1743-9779 (Online) Journal homepage: https://www.tandfonline.com/loi/rpos20 Revisiting the Sustainable Happiness Model and Pie Chart: Can Happiness Be Successfully Pursued? Kennon M. Sheldon & Sonja Lyubomirsky To cite this article: Kennon M. Sheldon & Sonja Lyubomirsky (2019): Revisiting the Sustainable Happiness Model and Pie Chart: Can Happiness Be Successfully Pursued?, The Journal of Positive Psychology, DOI: 10.1080/17439760.2019.1689421 To link to this article: https://doi.org/10.1080/17439760.2019.1689421 Published online: 07 Nov 2019. Submit your article to this journal View related articles View Crossmark data Full Terms & Conditions of access and use can be found at https://www.tandfonline.com/action/journalInformation?journalCode=rpos20 THE JOURNAL OF POSITIVE PSYCHOLOGY https://doi.org/10.1080/17439760.2019.1689421 Revisiting the Sustainable Happiness Model and Pie Chart: Can Happiness Be Successfully Pursued? Kennon M. Sheldona,b and Sonja Lyubomirskyc aUniversity of Missouri, Columbia, MO, USA; bNational Research University Higher School of Economics, Moscow, Russian Federation; cUniversity of California, Riverside, CA, USA ABSTRACT ARTICLE HISTORY The Sustainable Happiness Model (SHM) has been influential in positive psychology and well-being Received 4 September 2019 science. However, the ‘pie chart’ aspect of the model has received valid critiques. In this article, we Accepted 8 October 2019 start by agreeing with many such critiques, while also explaining the context of the original article KEYWORDS and noting that we were speculative but not dogmatic therein. We also show that subsequent Subjective well-being; research has supported the most important premise of the SHM – namely, that individuals can sustainable happiness boost their well-being via their intentional behaviors, and maintain that boost in the longer-term. -

Doing More with SAS/ASSIST® 9.1 the Correct Bibliographic Citation for This Manual Is As Follows: SAS Institute Inc
Doing More With SAS/ASSIST® 9.1 The correct bibliographic citation for this manual is as follows: SAS Institute Inc. 2004. Doing More With SAS/ASSIST ® 9.1. Cary, NC: SAS Institute Inc. Doing More With SAS/ASSIST® 9.1 Copyright © 2004, SAS Institute Inc., Cary, NC, USA ISBN 1-59047-206-3 All rights reserved. Produced in the United States of America. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, or otherwise, without the prior written permission of the publisher, SAS Institute Inc. U.S. Government Restricted Rights Notice. Use, duplication, or disclosure of this software and related documentation by the U.S. government is subject to the Agreement with SAS Institute and the restrictions set forth in FAR 52.227–19 Commercial Computer Software-Restricted Rights (June 1987). SAS Institute Inc., SAS Campus Drive, Cary, North Carolina 27513. 1st printing, January 2004 SAS Publishing provides a complete selection of books and electronic products to help customers use SAS software to its fullest potential. For more information about our e-books, e-learning products, CDs, and hard-copy books, visit the SAS Publishing Web site at support.sas.com/publishing or call 1-800-727-3228. SAS® and all other SAS Institute Inc. product or service names are registered trademarks or trademarks of SAS Institute Inc. in the USA and other countries. ® indicates USA registration. Other brand and product names are registered trademarks or trademarks of -
Crystal Imperfections-- Point, Line and Planar Defect
CRYSTAL IMPERFECTIONS: Introduction After studying the basics of crystallography, we arrived on one of the most important topics named Crystal Imperfection. Here we will be discussing the dimensional imperfection we encounter and its subtopics like the need to study, the cause behind the imperfection and the types of Imperfection we come across in a solid. We know about a crystal and its characteristics. And we also know that behind the ideality of theories in science, there is a reality of application in the true world. And in this topic, we will be encountering the reality. So, I will be defining an ideal crystal on the basis of facts provided to us till now. IDEAL CRYSTAL = Lattice + Motif An atom or group of 3 -D periodic atoms associated with each lattice arrangement of points Fig. 3-d representation of crystal of common salt The deviations we encounter in this set of ideal crystal, are termed as Defects or Imperfections. DEFINITION- Deviations in the regular geometrical arrangement of the atoms in a crystalline solid. Causes There can be a number of wanted and unwanted causes behind the defects that appear in a solid. Some are mentioned below: 1 .Deformation of solids (Alteration in size or shape of a body under the influence of mechanical forces) 2 3 4 .Rapid cooling from high temperature. .Crystallisation occurring at a differed rate. .High-energy radiation striking the solid. These reasons influence the mechanical, electrical, and optical behaviour of a crystal or a solid. Healthy Imperfections When we come across the word “Imperfection”, we assume that the thing for which this adjective is used is not perfect or worse than the perfect one. -

Vacancy Defect Positron Lifetimes in Strontium Titanate
1 Vacancy defect positron lifetimes in strontium titanate R.A. Mackie,1 S. Singh,1 J. Laverock, 2 S.B. Dugdale,2 and D.J. Keeble1,* 1Carnegie Laboratory of Physics, School of Engineering, Physics, and Mathematics, University of Dundee, Dundee DD1 4HN, UK 2 H.H. Wills Physics Laboratory, University of Bristol, Tyndall Avenue, Bristol BS8 1TL, UK *Corresponding author. Electronic address: [email protected] The results of positron annihilation lifetime spectroscopy measurements on undoped, electron irradiated, and Nb doped SrTiO3 single crystals are reported. Perfect lattice and vacancy defect positron lifetimes were calculated using two different first-principles schemes. The Sr vacancy defect related positron lifetime was obtained from measurements on Nb doped, electron irradiated, and vacuum annealed samples. Undoped crystals showed a defect lifetime component dominated by trapping to Ti vacancy related defects. 2 I. INTRODUCTION Vacancies are normally assumed to be the dominant point defects in perovskite oxide (ABO3) titanates, and often strongly influence the material properties such as electrical conductivity and domain stability and dynamics.1, 2 Strontium titanate is one of the most widely studied oxide materials, having a model cubic perovskite oxide structure at room temperature and exhibits an antiferrodistortive phase transition at 105 K. The material is a 0 3 wide band gap semiconductor (with Eg = 3.3 eV, ) but can be made a good conductor by 4 doping, for example, with Nb. Single crystal SrTiO3 substrates are readily available, and high quality epitaxial layers can be grown.5-7 The recent observation of two-dimensional 8 electron gas formation at the interface between SrTiO3 and LaAlO3, residing in the SrTiO3, has further demonstrated the importance of the material for future 9 multifunctional oxide electronic device structures. -

Miro Correlates with Other Psychometrics 13 Your Miro Practitioner 14
YOUR MIRO REPORT Adam Smith MiRo Behavioural Mode Assessment Table of Contents What does this report tell me? 3 The MiRo Behaviours Mode Summary Model 5 Your MiRo Behavioural Results 6 MiRo Correlates With Other Psychometrics 13 Your MiRo practitioner 14 Page 2 of 14 © MiRo Psychometrics Ltd 2015 What does this report tell me? Your personality is a particular pattern of behaviour and thinking prevailing across time and situations that differentiates one person from another. It is made up of many different elements, some innate, some learned. Apart from our inherited traits we develop ways of being and doing based on all kinds of good and bad experiences, value decisions and external influences. This complex system of attributes, behavioural temperament, emotions and mental energies is impossible to fully comprehend, let alone assess and quantify. Therefore the MiRo system looks at what can be observed, such as our habitual behaviours. These behaviours are determined by how we unconsciously perceive our environment and ourselves in relation to that environment. By measuring behaviour psychologists and psychotherapists such as William Marston and Carl Jung have indentified four main Behavioural Modes that are open to all of us. MiRo refers to these Modes as Driving, Energising, Organising and analysing and we use these Modes in order of our own preferences. Page 3 of 14 © MiRo Psychometrics Ltd 2015 The order of preference in which these behaviours are used is as follows: • Leading Behaviour which determines your main Behavioural traits • Supporting Behaviour which will act as a backup Behaviour to your Leading Behaviour • Supplementary Behaviourwhich can act to enhance your overall Behaviour • Dormant Behaviour which will be the Behaviour that you ignore Your MiRo results are based on the answers that you gave in your assessment, which is deliberately designed to force response based on habit and instinct.