Characterizing the Seasonal Cycle of Upper-Ocean Flows Under Multi-Year
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Page 1 57° 50° 40° 30° 20° 10° 0° -10° -20° -30° -40° -50° -57° 57° 50
180° 0° DODONA PLANUM 210° 330° 150° 30° 60° -60° . Bochica . Hatchawa Patera Patera . Nusku Patera . Hiruko Heno . Inti . Patera Patera Patera 70° -70° 240° 300° 60° 120° Tvashtar . Taranis Patera Iynx TARSUS Aramazd Mensa . Patera Tvashtar Paterae Haemus REGIO Montes Mensae LERNA REGIO 80° Echo -80°Mensa . Chors Nile Montes N Patera E M . Viracocha E Patera A 90° CHALYBES 270° 90° P 270° L A . Mithra N Patera U REGIO M . Vivasvant Patera . Crimea Mons 80° -80° Pyerun . Patera Dazhbog 120° 60° Patera . 300° 240° 70° -70° ILLYRIKON REGIO 60° -60° 30° 150° 330° 210° 0° 180° NORTH POLAR REGION SOUTH POLAR REGION 180° 170° 160° 150° 140° 130° 120° 110° 100° 90° 80° 70° 60° 50° 40° 30° 20° 10° 0° 350° 340° 330° 320° 310° 300° 290° 280° 270° 260° 250° 240° 230° 220° 210° 200° 190° 180° 57° 57° Nile Montes Dazhbog Patera CHALYBES REGIO 50° 50° . Kinich Ahau . Savitr Patera Patera Surt Zal Montes Lei-Kung Zal Fluctus . Fo Patera 40° 40° Patera Thor . Amaterasu . Dusura Patera Patera BULICAME . Manua Patera Shango REGIO Arinna . _ Patera Ukko . Atar Fluctus . Patera Patera Heiseb Isum 30° . 30° Fuchi Patera Patera Reshef Euxine . Patera Mons Patera Volund . Thomagata Amirani Patera . Shakuru Skythia Mons Girru . Mongibello . Tiermes Patera . Susanoo Donar Surya Estan Patera Patera . Patera Mons Patera Fluctus Patera Monan Daedalus 20° . Patera Loki . 20° Zamama Maui . Gish Bar Patera Mons Mulungu Steropes Maui . Patera . Patera Ruaumoko . Camaxtli Patera Gish Bar Sobo Patera . Patera Patera Fluctus Monan Loki Chaac . Ababinili Tien Mu Mons Llew . Balder Patera . Fjorgynn Patera . -
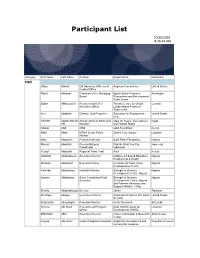
Participant List
Participant List 10/20/2019 8:45:44 AM Category First Name Last Name Position Organization Nationality CSO Jillian Abballe UN Advocacy Officer and Anglican Communion United States Head of Office Ramil Abbasov Chariman of the Managing Spektr Socio-Economic Azerbaijan Board Researches and Development Public Union Babak Abbaszadeh President and Chief Toronto Centre for Global Canada Executive Officer Leadership in Financial Supervision Amr Abdallah Director, Gulf Programs Educaiton for Employment - United States EFE HAGAR ABDELRAHM African affairs & SDGs Unit Maat for Peace, Development Egypt AN Manager and Human Rights Abukar Abdi CEO Juba Foundation Kenya Nabil Abdo MENA Senior Policy Oxfam International Lebanon Advisor Mala Abdulaziz Executive director Swift Relief Foundation Nigeria Maryati Abdullah Director/National Publish What You Pay Indonesia Coordinator Indonesia Yussuf Abdullahi Regional Team Lead Pact Kenya Abdulahi Abdulraheem Executive Director Initiative for Sound Education Nigeria Relationship & Health Muttaqa Abdulra'uf Research Fellow International Trade Union Nigeria Confederation (ITUC) Kehinde Abdulsalam Interfaith Minister Strength in Diversity Nigeria Development Centre, Nigeria Kassim Abdulsalam Zonal Coordinator/Field Strength in Diversity Nigeria Executive Development Centre, Nigeria and Farmers Advocacy and Support Initiative in Nig Shahlo Abdunabizoda Director Jahon Tajikistan Shontaye Abegaz Executive Director International Insitute for Human United States Security Subhashini Abeysinghe Research Director Verite -

Underlying Structural Control of Small-Scale Faults and Fractures in West Candor Chasma, Mars C
JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 117, E11001, doi:10.1029/2012JE004144, 2012 Underlying structural control of small-scale faults and fractures in West Candor Chasma, Mars C. Birnie,1 F. Fueten,1 R. Stesky,2 and E. Hauber3 Received 29 May 2012; revised 4 September 2012; accepted 18 September 2012; published 2 November 2012. [1] Orientations of small-scale faults and fractures within the interior layered deposits of West Candor Chasma were measured to investigate what information about the geologic history of Valles Marineris they can contribute. Deformational features were separated into six categories based on morphology and their orientations were analyzed. The elevations at which the deformational features formed are recorded, as a proxy for stratigraphic level. Deformational features occur over a continuous range of elevations and display regionally consistent preferred orientations, indicating their formation was controlled by a regional stress regime. The two most abundant preferred orientations of 35 and 110 are approximately parallel to the chasma walls and the inferred underlying normal faults. The alignment of three populations of small faults at 140, consistent with the morphology of release faults, indicates a large-scale fault underlying the southeastern border of Ceti Mensa. The preferred orientations imply these small-scale deformational features formed from a continuation of the same imposed stresses responsible for the formation of Valles Marineris, indicating these stresses existed past the formation of the interior layered deposits. The origins of a fourth preferred orientation of 70 is less clear but suggests the study area has undergone at least two periods of deformation. Citation: Birnie, C., F. -

History of Outflow Channel Flooding from an Integrated Basin System East of Valles Marineris, Mars
47th Lunar and Planetary Science Conference (2016) 2214.pdf History of Outflow Channel Flooding from an Integrated Basin System East of Valles Marineris, Mars. N. Wagner1, N.H. Warner1, and S. Gupta2, 1State University of New York at Geneseo, Department of Geological Sciences, 1 College Circle, Geneseo, NY 14454, USA. [email protected]. 2Earth Science and Engineering, Imperial College London, South Kensington Campus, London, SW7 2AZ, United Kingdom Introduction: The eastern end of Valles Marineris [6, 7], including all craters with diameters > 200 m in includes diverse terrain formed from extensional forces the count. and collapse due to groundwater release. Capri For the paleohydrology analysis, the topographic Chasma, Eos Chaos, Ganges Chasma, and Aurorae characteristics and dimensions of each channel were Chaos (Fig. 1) were all likely formed due to a measured using the HRSC DTM. Paleo-flow depths combination of these processes [1,2]. were determined based on the observation of trimlines Importantly, this region shows evidence that that mark the margins of individual bedrock terraces. significant volumes of overland water flow travelled These terraces were first identified by [4] and have through this integrated basin system [3,4,5]. been mapped here within every outlet channel that Furthermore, recent studies have suggested that liquid exits an upstream basin. The presence of multiple water was at least temporarily stable here [4]. The bedrock terraces and trimlines indicates that the topographic and temporal relationships between Eos channels were formed by progressively deeper incision Chaos and its associated outflow channels for example and also suggests that bankfull estimates of these demonstrate that the upstream chaotic terrains pre-date channels are gross over-estimates. -

Nüwa, a Self-Sustainable City State on Mars – Development Concept, Urban Design and Life Support
50th International Conference on Environmental Systems ICES-2021-225 12-15 July 2021 Nüwa, a self-sustainable city state on Mars – development concept, urban design and life support Gisela Detrell1 University of Stuttgart, Stuttgart, Germany Alfredo Muñoz2 ABIBOO Studio, New York, USA Miquel Banchs-Piqué3 University of Portsmouth, Portsmouth, UK Guillem Anglada4,5 Institut de Ciències de l'Espai/CSIC, Barcelona, Spain Institut d'Estudis Espacials de Catalunya (IEEC), Barcelona, Spain Philipp Hartlieb6 Montanuniversitaet Leoben, Leoben, Austria Miquel Sureda7 UPC-BarcelonaTECH, Barcelona, Spain Mars is one of the current targets for human space exploration. The first settlement will most likely include a small group of explorers, but with time, it is reasonable to assume that a city on Mars might grow and become a reality. Nüwa is a project of the Sustainable Off-world Network (SONet), a network of interdisciplinary and international professionals, dedicated to the development of sustainable human settlements beyond Earth. This project focuses on engineering and architecture, but also on sustainable growth planning of a society on the red planet. The design consists of five cities, with 200,000 inhabitants each. Different locations strategically selected ensure in-situ resource utilization. The city concept is based on a tunneling system on cliffs. The design of a big city in the harsh Mars environment poses several challenges and is a complex and broad task. Further research in all fields is required. This paper focuses on three aspects of the design: development concept, urban planning and Life Support. The city needs to provide a safe environment for the inhabitants, but also provide all required services and a practical and enjoyable place to live. -

Sulfur on Mars from the Atmosphere to the Core Heather B
Sulfur on Mars from the Atmosphere to the Core Heather B. Franz1, Penelope L. King2, and Fabrice Gaillard3 1NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA 2Research School of Earth Sciences, Australian National University, Canberra ACT 2601, Australia 3CNRS-Université d’Orléans, ISTO, la rue de la Ferollerie, 45071 Orléans, France Abstract Observations of the martian surface from orbiting spacecraft and in situ landers and rovers, as well as analyses of martian meteorites in terrestrial laboratories, have consistently indicated that Mars is a sulfur-rich planet. The global inventory of sulfur, from the atmosphere to the core, carries widespread implications of potential geophysical, geochemical, climatological, and astrobiological significance. For example, the sulfur content of the core carries implications for core density; the speciation of igneous sulfur minerals reflects the oxidation state of the magma from which they formed; sulfur-bearing gases may have exerted control on the temperatures at the surface of early Mars; and the widespread availability of sulfur on Mars would have provided an abundant source for energy and nutrients to fuel sulfur-metabolizing microbes, such as those that arose during the emergence of primitive life on Earth. Here we provide an overview of martian sulfur and its relevance to these areas of interest, including a discussion of analytical techniques and results acquired by space missions and meteorite analyses to date. We review current studies modeling the potential effects of sulfur-bearing gases on the past martian climate and possible constraints on atmospheric composition implied by sulfur isotopic data. We also explore the importance of sulfur to the search for extinct or extant life on Mars. -

USAFA Application
Campus Box 8208 College of Sciences 1125 Jordan Hall Department of Marine Earth & Atmospheric Sciences 2800 Faucette Drive [email protected] (704) 747-4189 Raleigh, NC 27695-8208 meas.ncsu.edu Curriculum Vitae Colonel (Ret) Julian Matthews Chesnutt Geology Ph.D. Candidate, Adjunct Professor, Lecturer and Teaching Assistant Education ● Completed all Geology Ph.D. coursework with a 4.01 GPA for a combined 3.872 Graduate work GPA ● Unconditionally passed both oral and written Geology Ph.D. qualification exams ● Graduate Certificate in Geospatial Information Science, North Carolina State University, Raleigh NC—2017 o Earned at 4.167 GPA in the GIS Graduate Certificate Program ● National Defense Fellow, Institute for the Study of Diplomacy, Georgetown University, Washington DC—2009 ● Master of Military Operational Art & Science, School of Advanced Air and Space Studies, Maxwell AFB AL—2004 ● Master of Operational Art, Air Command and Staff College, Distinguished Graduate, Maxwell AFB AL—2003 ● Master of Engineering in Materials Science, North Carolina State University, Raleigh NC—1996 ● Bachelor of Science in Space Physics, Distinguished Graduate, US Air Force Academy, Colorado Springs CO—1989 Teaching Accomplishments • Environmental Geology (GEL 230) Lecturer & Lab Adjunct Professor, Durham Technical Community College—2019 ● Planetary Geology (ERS 131, ERS 132) Course Developer, Lecturer & Lab Adjunct Professor, NC Wesleyan University—2018 ● Physical Geology (MEA 101, MEA 111) Lecturer, Lab Instructor & Teaching Assistant at NC State University—2016-2019 -

Evolution of Major Sedimentary Mounds on Mars: Build-Up Via Anticompensational Stacking Modulated by Climate Change
Evolution of major sedimentary mounds on Mars: build-up via anticompensational stacking modulated by climate change Edwin S. Kite1,*, Jonathan Sneed1, David P. Mayer1, Kevin W. Lewis2, Timothy I. Michaels3, Alicia Hore4, Scot C.R. Rafkin5. 1. University of Chicago. 2. Johns Hopkins University. 3. SETI Institute. 4. Brock University. 5. Southwest Research Institute. (*[email protected]) Abstract. We present a new database of >300 layer-orientations from sedimentary mounds on Mars. These layer orientations, together with draped landslides, and draping of rocks over differentially- eroded paleo-domes, indicate that for the stratigraphically-uppermost ~1 km, the mounds formed by the accretion of draping strata in a mound-shape. The layer-orientation data further suggest that layers lower down in the stratigraphy also formed by the accretion of draping strata in a mound-shape. The data are consistent with terrain-influenced wind erosion, but inconsistent with tilting by flexure, differential compaction over basement, or viscoelastic rebound. We use a simple landscape evolution model to show how the erosion and deposition of mound strata can be modulated by shifts in obliquity. The model is driven by multi-Gyr calculations of Mars’ chaotic obliquity and a parameterization of terrain-influenced wind erosion that is derived from mesoscale modeling. Our results suggest that mound-spanning unconformities with kilometers of relief emerge as the result of chaotic obliquity shifts. Our results support the interpretation that Mars’ rocks record intermittent liquid-water runoff during a 108-yr interval of sedimentary rock emplacement. 1. Introduction. Understanding how sediment accumulated is central to interpreting the Earth’s geologic records (Allen & Allen 2013, Miall 2010). -

Planetary Nomenclature: Overview and Update for 2020
51st Lunar and Planetary Science Conference (2020) 2237.pdf PLANETARY NOMENCLATURE: OVERVIEW AND UPDATE FOR 2020. T. A. Gaither1, K. Aksnes2, G. A. Burba3, G. J. Consolmagno5, R. M. C. Lopes6, P. Masson7, W. Sheehan8, G. V. Williams9, and C. Wood10, 1USGS Astrogeology Science Center, Arizona, USA, [email protected], 2ESA Science Directorate, ESTEC, Noordwijk, The Netherlands, 3Institute for Theoretical Astrophysics, Oslo, Norway, 4Vernadsky Institute, Moscow, Russia, 5Specola Vaticana, Vatican City State, 6Jet Propulsion Laboratory, California Institute of Technology, California, USA, 7Universite de Paris-Sud, Orsay, France, 8Lowell Observatory, Arizona, USA, 9 Minor Planet Center, Massachusetts, USA, 10Planetary Science Institute, Arizona, USA. Introduction: The task of naming planetary surface • Solar system nomenclature should be inter- features, rings, and natural satellites is managed by the national in its choice of names. International Astronomical Union’s (IAU) Working • Names having political, military, or religious Group for Planetary System Nomenclature (WGPSN). significance are not allowed. The volunteer members of the WGPSN and its task • Commemoration is not a goal in itself, but may be groups have worked since the early 1970s to provide a employed in special circumstances and is reserved for clear, unambiguous system of planetary nomenclature persons of high and enduring international standing. that represents cultures and countries from all regions of Persons being so honored must have been deceased for Earth. Since the 1980s, the USGS Astrogeology Science at least three years. Center has managed (for the IAU and with the financial Guidelines for Requesters: An official name may support of NASA) the ever-growing database of be requested for any unnamed morphological or planetary names and the Gazetteer of Planetary topographic feature that will be a primary focus of a Nomenclature website. -

Lobate Scarps and the Martian Crustal Dichotomy Thomas R
JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 104, NO. E8, PAGES 18,981–18,990, AUGUST 25, 1999 Lobate scarps and the Martian crustal dichotomy Thomas R. Watters Center for Earth and Planetary Studies, National Air and Space Museum Smithsonian Institution, Washington, D.C. Mark S. Robinson Department of Geological Sciences, Northwestern University, Evanston, Illinois Abstract. Landforms reflecting crustal shortening are found in the ancient highlands of the eastern hemisphere of Mars. These structures, referred to as lobate scarps, are interpreted to be thrust faults. Lobate scarps occur near and are oriented roughly parallel to the Martian crustal dichotomy, a major geologic and topographic boundary that divides the heavily cratered highlands from the relatively smooth, featureless northern lowlands. The long- and short-wavelength topography of lobate scarps in the northern Terra Cimmeria–Amenthes region have been analyzed using photoclinometry, Earth-based radar altimetry, and Mars Orbiter Laser Altimeter data. The measured relief of lobate scarps in this region ranges from ϳ110 to 1230 m, and they occur on gentle regional slopes that dip both toward and away from the dichotomy. Estimates of the horizontal shortening across the lobate scarps studied range from roughly 0.24 to 2.6 km (n ϭ 9), assuming fault plane dips of 25Њ. The displacement-length (D-L) relationships of thrust faults associated with the lobate scarps are consistent with those observed for terrestrial fault populations. The compressional strain in the heavily cratered highlands near the dichotomy, determined using the D-L data for the lobate scarps, is estimated to be ϳ0.17%. Topographic data indicate that the dichotomy in the northern Terra Cimmeria–Amenthes region has a distinct topographic signature. -

Echus Chasma and Kasei Valles, Mars: New Data and Geologic Interpretations
Lunar and Planetary Science XXXVIII (2007) 1407.pdf ECHUS CHASMA AND KASEI VALLES, MARS: NEW DATA AND GEOLOGIC INTERPRETATIONS. M. G. Chapman1, G. Neukum2, S. C. Werner3, S. van Gasselt2, A. Dumke2, W. Zuschneid2, and G. Michael2; 1 U.S. Geological Survey, Flagstaff, AZ, 86001, USA ([email protected]); 2Institute of Geosciences, Freie Uni- versitaet Berlin, 12249 Germany; 3Geological Survey of Norway (NGU), 7491 Trondheim, Norway. Introduction: Echus Chasma is a 175-km-wide, features of lavas in the area and as its trend is parallel 100-km-long open-ended depression at lat. 1°S, long. to ancient flood scour, the dorsum may be related to 80°W. Kasei Valles extends nearly 3000 km north the Tharsis floods (levee or medial ridge?). Images from Echus Chasma and then east at lat. 20°N, long indicate the ridge was flood scoured. [Scouring also 75° W. to debouch into Chryse Planitia. Previous appears to have plucked unit At4 northwest of Labeatis mapping indicated the chasma and valles system cut Mensa.] Uranius Dorsum bounds the northeast part of into Hesperian ridged plains material (unit Hpr) of the a large lava-covered MOLA topographic low, centered Lunae Planum and Tempe Terra plateaus, and that west of Kasei Valles (at lat. 18°N., long. 81° W.) that Tharsis lava units At4 and At5 of Amazonia age cover extends to long 84°W., which is about 420 km away large parts of the channel [1-4]. Across north Kasei, from the previous mapped boundary [8,9] of Kasei. the older unit At4 flows are sourced east from Tharsis. -

Sustained Fluvial Deposition Recorded in Mars’ Noachian Stratigraphic
ARTICLE https://doi.org/10.1038/s41467-020-15622-0 OPEN Sustained fluvial deposition recorded in Mars’ Noachian stratigraphic record ✉ Francesco Salese 1,2,6 , William J. McMahon1,6, Matthew R. Balme3, Veronique Ansan 4, Joel M. Davis5 & Maarten G. Kleinhans 1 Orbital observation has revealed a rich record of fluvial landforms on Mars, with much of this record dating 3.6–3.0 Ga. Despite widespread geomorphic evidence, few analyses of Mars’ 1234567890():,; alluvial sedimentary-stratigraphic record exist, with detailed studies of alluvium largely lim- ited to smaller sand-bodies amenable to study in-situ by rovers. These typically metre-scale outcrop dimensions have prevented interpretation of larger scale channel-morphology and long-term basin evolution, vital for understanding the past Martian climate. Here we give an interpretation of a large sedimentary succession at Izola mensa within the NW Hellas Basin rim. The succession comprises channel and barform packages which together demonstrate that river deposition was already well established >3.7 Ga. The deposits mirror terrestrial analogues subject to low-peak discharge variation, implying that river deposition at Izola was subject to sustained, potentially perennial, fluvial flow. Such conditions would require an environment capable of maintaining large volumes of water for extensive time-periods, necessitating a precipitation-driven hydrological cycle. 1 Faculty of Geosciences, Utrecht University, Princetonlaan 8a, , Utrecht 3584 CB, The Netherlands. 2 International Research School of Planetary Sciences, Università Gabriele D’Annunzio, Viale Pindaro 42, , Pescara 65127, Italy. 3 Planetary Environments Group, Open University, Walton Hall, Milton Keynes, UK. 4 LPG Nantes, UMR6112, CNRS-Université de Nantes, 2 rue de la Houssinère, BP 92208, 44322 Nantes Cedex 3, France.