DOCSLIB.ORG

MAA Sections | Mathematical Association of America

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
MAA Sections | Mathematical Association of America Annual Meeting of the Pacific Northwest Section of the MATHEMATICAL ASSOCIATION OF AMERICA Willamette University Salem, Oregon April 12–13, 2013 1 Annual Meeting of the Pacific Northwest Section of the Mathematical Association of America Sponsored & Hosted by Willamette University Mathematics Department College of Liberal Arts Salem, Oregon April 12–13, 2013 Friday, April 12 7:45 Packet pickup for Project NExT Ford 102 8:00 Project NExT Meeting Ford 102 2:30 3:00 Minicourse: Minicourse: Closer to Fair: Social Justice in Mathematics, Cryptology [2] Mathematics for Social Justice [1] Ford 201 Ford 204 5:30 Student Reception Project NExT Dinner (No Host) & Discussion & Packet Pickup 5:45 The Ram 7:00 Restaurant and Brewery Packet Pick-up1 515 12th Street Ford 2nd Floor Hearth Ford 2nd Floor Hearth 503.363.1904 8:00 Friday Evening Lecture: Liz McMahon Error Detection and Correction in the Card Game SETTM [3] Montag Center 9:15 Reception Montag Center 10:15 1Packet pickup will also be available in Ford 2nd Floor Hearth from 2:00-3:30 2 Saturday, April 13 7:45 Executive Committee Meeting 8:00 Ford 222 Ford Hall 9:15 Introduction and Welcome: Packet Pickup Stephen E. Thorsett, & Registration Willamette University President Ford 2nd Floor Hearth Invited Talk: Frank Farris Undercover Symmetry [4] Cone Chapel, Waller Hall 10:45 Contributed Talks Ford Hall 102, 201, 204, 222, 301, 302, 304 12:45 Lunch (provided) Cat Cavern, University Center 2nd Floor 1:15 Business Meeting 1:50 Cat Cavern, Dining Rooms 1 & 2 2:00 Invited Talk: David Kung Symphonic Equations: A Mathematical Exploration of Music [5] Cone Chapel 3:00 Waller Hall 3:15 Contributed Talks Ford Hall 102, 201, 204, 301, 302, 304 5:45 Social Hour University Center 2nd Floor 7:00 Banquet Dinner - Section Awards Cat Cavern, University Center 2nd Floor 8:30 Invited Lecture: Liz McMahon Mathematics in the Game of SETTM [6] Cone Chapel Waller Hall 3 Program of Contributed Papers The program of contributed papers appears on the following pages. In some cases, titles or other information are abbreviated for reasons of space; please see the full abstract for more information. A dagger (†) indicates which contributor(s) will present when multiple contributors are listed and fewer are presenting the work. An asterisk (∗) indicates the contributor is an undergraduate student. Double asterisks (∗∗) indicate the contributor is a graduate student. Session Organizers • Math Circles & Math Teachers’ Circles: Mathematical Problem Solving for Students and Teachers: David Scott, University of Puget Sound • Games : Mary Riegel and Jenny McNulty, University of Montana • Accommodations for Students with Low-Incidence Disabilities in College Mathematics : Paul Krouss, Washington State University, Vancouver • Junior Faculty Research: Hannah Callender, University of Portland • Undergraduate Research: Dominic Klyve, Central Washington University • General Contributed Papers: Chuck Dunn, Linfield College Please contact the session organizer with any questions about a session. Moderators: Please start each talk on time, but not early. Meeting participants often move between sessions and will want to be there when the talks are scheduled to begin. 4 Contributed Talks – Saturday Morning Interactive Session: Games Junior Faculty Accommodations Research Ford 222 Ford 201 Ford 204 10:45–11:00 Designer Board Games for A Somewhat Constructive Interactive Session the Interested Approach to the Mountain Mathematician [46] Pass Lemma and Its Variants [12] Paul Krouss, WSU Vancou- ver: Organizer Speakers: Josh Laison, WU James Bisgard, CWU 11:05–11:20 Accommodating Blind Turning off the Lights [30] Generating the Brauer Students in College Group of the Function Field Mathematics; An Amateur’s of a p-adic Curve [53] Guide [45] Paul Krouss, WSU Vancouver Gary Gordon, Lafayette College Kelly McKinnie, UMT 11:25–11:40 A Math Accommodation Introduction to Competitive Using Spatiotemporal Brain Success Story [49] Graph Coloring [24] Connectivity Matrices to Estimate Cortical Activity from EEG [32] Zach Lattin, Washington State School for the Blind Chuck Dunn, Linfield David Hammond, UO 11:45–12:00 Competitive Graph Coloring Methods for High- on Complete Multipartite Dimensional Multivariate Graphs [60] Repeated Measures Data under General Conditions [36] Nino Barrett, University of Rochester∗ Chuck Dunn, Linfield Jennifer Nordstrom, Linfield John Portin, Linfield †∗ Alexander Sistko, Bradley University∗ John Hossler, SPU 12:05–12:20 Modeling the Game “7 Undergraduate Speed Wonders” [29] Research, and the Sum-of-Divisors [41] Ben Gardiner, WU Dominic Klyve, CWU 12:25–12:40 FIRE and ICETM [63] Emergent Reducibility of Cubic Polynomials [61] Mary Riegel, UMT Jason Preszler, UPS 5 Contributed Talks – Saturday Morning Student Papers 1 Student Papers 2 Ford 301 Ford 302 10:45–11:00 To Reach a Sum on Dice Student Success in [18] Prerequisite-Linked Mathematics Courses [11] Karen Cole, WOU ∗ Peter Banwarth , OSU∗∗ 11:05–11:20 A Representation of SO(4,2) The Cost of Drunkenness for [39] the Game of Cops and Robbers [69] Tevian Dray, OSU ∗ Josh Kincaid, OSU†∗ Molly Stubblefield, WOU 11:25–11:40 Exploring Infinite Sequences Relations between Klein of Hitches [47] Knots and Torus Knots I [8] Enrique Alvarado, Hanna Landrus, PU∗ Gonzaga∗ 11:45–12:00 Analysis of the Hammer Relations between Klein Throw [48] Knots and Torus Knots II [62] Brandon Reeves, Jennifer Larson, WOU∗ Gonzaga∗ 12:05–12:20 Mathematical Illiteracy A Model: Pollution Decay Causes Financial Collapse: and Purification of Lake Incorrect Implementation of Onondaga [16] the Black-Scholes Model [50] Kaci Linton, PU∗ Lindsay Callahan, WOU∗ 12:25–12:40 Searching for Optimal Book Euclidean Tessellations and Embeddings for Families of Regular Polygons in the Graphs [52] Taxicab Plane [58] Lauren Joplin, PU∗ Maria Mai, PU∗ Thomas Pitts, OSU∗ 6 Contributed Talks – Saturday Morning Student Papers 3 General Papers 1 Ford 102 Ford 304 10:45–11:00 Dining Etiquette and Oral Reviews in Calculus: Combinatorics [43] Improving Student Understanding [34] Isaiyah Kovachy, WOU ∗ Allison Henrich, SU 11:05–11:20 Zero-Divisor Graphs of 2 × 2 ‘Hanging Ten’: Measuring Matrix Algebras [13] Big Wave Intensities [51] Meghan Blanchet, Nancy Livingston Potter, Gonzaga∗ CPTC 11:25–11:40 A Note on l-Permutations Orthogonal Cayley-Sudoku [73] Tables [77] Madelyn Twain, WOU∗ Mike Ward, WOU 11:45–12:00 Examining Tangle A Course in Spherical Compositions and Their Geometry for Implications to Tricolorability Undergraduates [78] [17] Marshall Whittlesey, Christopher Cericola, SU∗ CSUSM 12:05–12:20 Approximating Square Roots Who is Prepared for from the Integers to the Calculus 1? [79] Modulars [10] Jennifer AnDyke, WOU∗ Nicholas Willis, GFU 12:25–12:40 Euclidean Constructions and Both Teams Played Hard: the Geometry of Origami Methods for Ranking [80] Basketball Teams [31] Jonathan Woodruff, WOU∗ Chris Hallstrom, UP 7 Contributed Talks – Saturday Afternoon Games/Math Circles Student Papers 4 Student Papers 5 Ford 201 Ford 204 Ford 301 3:15–3:30 What Do Games Tell Us Dropping the Lowest Score: Stable and Instability: Affine About Graphs? [59] A Mathematical Analysis of a Drama of Transformations Common Grading Practice [70] [14] Erika Stutts∗and Michael Demitri Plessas, UMT Rosie Brown, WOU∗ Vandeberg∗, GFU 3:35–3:50 The Link Smoothing Game Dodgson’s Condensation Custom Locks: Counting the [37] Method for Calculating Combinations [71] Determinants [22] Micah Donor∗and Mitch Inga Johnson, WU Main∗, GFU Christopher Tasner, WOU∗ 3:55–4:10 Navajo Nation Math Circles Zero-Sum Games [26] Exotic Vector Spaces [66] Project [67] Sarah Gilmore∗and Josiah Tatiana Shubin, SJSU Jose Figueroa, WOU∗ Shoemaker∗, GFU 4:15-4:30 Notes from the Missoula The Prime Values of a Perfect Shuffling [27] Math Circle [54] Quadratic Polynomial [9] Kelly McKinnie, UMT Matt Anderson, WU∗ Emily Flora, WOU∗ 4:35-4:50 What is a Math Wrangle? The Spider and the Fly [76] Computer AI for the Game of [67] Go [25] Zihao Wang∗and Hailey Tatiana Shubin, SJSU Meekins∗, GFU Kyle Evitts∗†et al., Linfield 4:55-5:10 What Makes a Math Winning at Rock, Paper, Newcastle Disease in Wild Teachers’ Circle [64] Scissors [42] Parrots: Building a Mathematical Model [33] Tyler Koglin∗and Jake David Scott, UPS Larson∗, GFU Cassy Hanson, WOU∗ 8 Contributed Talks – Saturday Afternoon General Papers 2 Student Papers 6 Student Papers 7 Ford 302 Ford 304 Ford 102 3:15–3:30 Linear Algebra and Digital Mathematical Resilience in Application of Polya´ Signal Processing [7] Biological Systems [38] Enumeration Theorem to Non-Isomorphic Graphs [35] Mohamed Allali, Chapman University Eric Keller, UAS∗ Sky Hester, WWU ∗ 3:35–3:50 A Hybrid Statistical and How Art Can Become Iterative Congressional Point-Neuron Simulation Mathematical Proof? [75] Redistricting [40] Environment for Neuronal Simulation [15] Nicholas Cain, Allen Institute Debra Virden, WOU∗ Evan Kleiner, Whitman∗ 3:55–4:10 Teaching Calculus for Generalized Ramsey Ta-Yen Encryption [44] Transfer, Assessing Numbers for Near-Diagonal Conceptual Understanding Pan Graphs and Relatively [19] Prime Tadpole Graphs [56] Noelle Conforti Preszler, UW Jason Preszler, University of Puget Sound Timothy Perisho, SPU∗ Anna Kralovec, WOU∗ 4:15-4:30 What’s New in WeBWorK Cyclic Permutations of Claps The Combinatorial Structure [20] and Patterns [74] of PS-Ear Decomposable Graphs [57] Nima Imani, UW ∗ Lee Johnson, SU ∗ McKenzie Keeling-Garcia, SU ∗ Steven Klee, SU ∗ Robin Cruz, C of I Cydney Tyler, WOU Casey Pinckney, SU †∗ 4:35-4:50 Cubies
Load more

Recommended publications
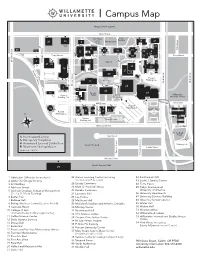
  • To Download a Map of the Willamette University Campus. Look for Building #29
    willamette university campus map Oregon State Capitol State Street Star Trees Star Trees 22 21 35 3 20 25 15 11 44 34 50 16 8 5 32 Ferry Street 51 41 42 Ferry Street Cottage Street 14 39 9 Quad 7 17 27 13 1033 47 6 10 30 18 19 29 46 43 Mission Street Permit Street Street Mill Race Parking Lot th th 23 12 14 P r Jackson in g Plaza l 24 e P 4 a 53 r k 38 w 37 45 a y Permit Hatfield Parking Lot 28 Fountain Mill Street Mill Street Permit Sparks Field 49 1 Parking Lot 48 Winter Street 40 36 12 52 Permit 2 Parking Lot 26 Permit Parking Lot Tennis Courts Bellevue Street Softball Field Parking Oak Street Lot Leslie Street Capitol Street University Street Mission Street 31 1 Admission Office (CLA) 21 Hallie Ford Museum of Art 40 Shepard House 2 Alpha Chi Omega Sorority 22 Gatke Hall 41 Sigma Chi Fraternity 3 Art Building 23 Goudy Commons 42 Sigma Alpha Epsilon Fraternity 4 Atkinson Graduate School of Management 24 Mark O. Hatfield Library 43 Smith Auditorium (Seeley G. Mudd Building) 25 Haseldorf Apartments 44 Smullin Hall 5 Baxter Hall 26 Kaneko Commons 45 Lestle J. Sparks Center 6 Belknap Hall 27 Lausanne Hall 46 Terra House 7 Beta Theta Pi Fraternity 28 Lee House 47 Theatre Playhouse 8 Bishop Wellness Center 29 Mary Stuart Rogers Music Center 48 Tokyo International 9 Campus Safety (Hudson Hall) University of America 10 College of Law 30 Matthews Hall 49 University Apartments (Truman Wesley Collins Legal Center) 31 McCulloch Stadium and Athletics Complex 50 Waller Hall* 11 Collins Science Center 32 Montag Center 51 Walton Hall 12 Delta Gamma Sorority 33 Office of International Education 52 Willamette International Studies House 13 Doney Hall and the Writing Center (WISH) 14 Doney North Offices* 34 Olin Science Center 53 York House 15 East House 35 Oregon Civic Justice Center * See reverse side for specific 16 Eaton Hall 36 Pi Beta Phi Sorority offices within the building.
    [Show full text]
  • Campus Map Front 6-24-14
    Campus Map Oregon State Capitol State Street Rose Garden 23 36 3 50 Star Trees North Lawn 22 24 34 26 th Street 3 10 12 44 1 54 35 51 15 8 65 33 Ferry Street 52 53 45 Ferry Street Church Street 4 Cottage Street 41 Quad 17 9 29 14 10 19 37 7 31 11 P 21 20 40 r 47 in 16 g 43 le P a r Permit Street k w Mill Race Parking Lot th th Street 2 4 a 25 1 1 y Jackson Winter Street Plaza 27 5 56 39 18 46 Permit Brown Field Hatfield Willamette Parking Lot 30 Fountain Heritage Center Sky Bridge Mill Street Mill Street Permit Parking Lot 49 1 Sparks Field 48 55 Permit 42 38 13 2 Parking Lot 28 Visitor Parking Lot Tennis Courts Bellevue Street Softball Field Handicapped Access Oak Street t Emergency Telephone t Automated External Defibrillator Salem Hospital Parking Lot Short-term Parking Meters Leslie Street Updated: 6/24/14 Capitol Stree University Stree Mission Street Bush’s Pasture Park 32 1 Admission Office (College of Liberal Arts) 20 Fine Arts East 41 Service Center (moving to the Visit Center [50] Winter Term) 21 Fine Arts West (including Campus Safety) 2 Alpha Chi Omega Sorority 22 Ford Hall 42 Shepard House 3 Art Building 23 Hallie Ford Museum of Art 43 Smith Auditorium 4 Atkinson Annex 24 Gatke Hall 44 Smullin Hall 5 Atkinson Graduate School of Management 25 Goudy Commons 45 Southwood Hall (Seeley G. Mudd Building) 26 Haseldorf Apartments 46 Lestle J.
    [Show full text]
  • Interpretation and Conclusions
    "LIKE NUGGETS FROM A GOLD MINEu SEARCHING FOR BRICKS AND THEIR MAKERS IN 'THE OREGON COUNTRY' B~f' Kmtm (1 COfwer~ ;\ th¢...i, ...uhmineJ Ilt SOIl(mla Slale UFU vcr,il y 11'1 partial fulfiUlT'Ietlt of the fCqlJln:mcntfi for the dcgr~ of MASTER OF ARTS tn Copyright 2011 by Kristin O. Converse ii AUTHORlZAnON FOR REPRODUCnON OF MASTER'S THESISIPROJECT 1pM' pernlt"j(m I~ n:pnll.lm.:til.m of Ihi$ rhais in ib endrel)" \Ii' !tbout runt\er uuthorilAtlOO fn.)m me. on the condiHt)Jllhat the per",)f1 Of a,eocy rl;!'(lucMing reproduction the "'OS$. and 1:Jf't)vi~ proper ackruJwkd,rnem nf auth.:If'l'htp. III “LIKE NUGGETS FROM A GOLD MINE” SEARCHING FOR BRICKS AND THEIR MAKERS IN „THE OREGON COUNTRY‟ Thesis by Kristin O. Converse ABSTRACT Purpose of the Study: The history of the Pacific Northwest has favored large, extractive and national industries such as the fur trade, mining, lumbering, fishing and farming over smaller pioneer enterprises. This multi-disciplinary study attempts to address that oversight by focusing on the early brickmakers in „the Oregon Country‟. Using a combination of archaeometry and historical research, this study attempts to make use of a humble and under- appreciated artifact – brick – to flesh out the forgotten details of the emergence of the brick industry, its role in the shifting local economy, as well as its producers and their economic strategies. Procedure: Instrumental Neutron Activation Analysis was performed on 89 red, common bricks archaeologically recovered from Fort Vancouver and 113 comparative samples in an attempt to „source‟ the brick.
    [Show full text]
  • Campus Map Front 7-24-17
    Campus Map Oregon State Capitol State Street Star Trees Rose Garden 20 33 3 North Lawn 19 21 31 th Street 3 48 11 41 1 52 32 49 14 22 65 8 30 Ferry Street 50 51 42 Ferry Street Church Street 4 Cottage Street 13 Quad 9 47 38 26 10 34 7 28 10 P 18 17 37 r 44 in 15 g 40 le P a r Permit Street k w Mill Race Parking Lot th th Street 2 4 a 23 1 1 y Jackson Winter Street Plaza 24 5 54 36 16 Brown 43 Permit Field Hatfield Willamette Parking Lot 27 Fountain Heritage Center Sky Bridge Mill Street Mill Street Permit Parking Lot 46 1 Sparks Field 45 53 Permit 39 35 12 2 Parking Lot 25 Visitor Parking Lot Tennis Courts Bellevue Street Softball Field Handicapped Access Oak Street t Emergency Telephone t Automated External Defibrillator Salem Hospital Parking Lot Short-term Parking Meters Leslie Street Updated: 7/24/17 Capitol Stree University Stree Mission Street Bush’s Pasture Park 29 1 Admission Office (undergraduate) 22 Global Learning Center (including 42 Southwood Hall 2 Alpha Chi Omega Sorority International Education) 43 Lestle J. Sparks Center 3 Art Building 23 Goudy Commons 44 Terra House 4 Atkinson Annex 24 Mark O. Hatfield Library 45 Tokyo International 5 Atkinson Graduate School of Management 25 Kaneko Commons University of America (Seeley G. Mudd Building) 26 Lausanne Hall 46 University Apartments 6 Baxter Hall 27 Lee House 47 University Services Building 7 Belknap Hall 28 Matthews Hall 48 University Services Annex 8 Bishop Wellness Center (Student Health) 29 McCulloch Stadium and Athletics Complex 49 Waller Hall 9 Cascadia House 30 Montag Center 50 Walton Hall 10 College of Law 31 Northwood Hall 51 Westwood Hall (Truman Wesley Collins Legal Center) 32 Olin Science Center 52 Willamette Academy 11 Collins Science Center 33 Oregon Civic Justice Center 53 Willamette International Studies House (WISH) 12 Delta Gamma Sorority 34 M.
    [Show full text]
  • Extra Credit Opportunity: Salem—Willamette University
    Extra Credit Opportunity: Salem—Willamette University Write a ½ to 1 page summary and reflection about this lecture. Turn in next class day: Tuesday March 11. Or if you stay in Salem for the evening lecture, you can turn it in on Thursday, March 13. Alternative Energy: Implications of Liquefied Natural Gas (LNG) Monday, Mar 10th 2008 4:00pm - 5:00pm Hatfield Room Willamette University See next page for directions to campus and map of campus Did you know that energy speculators are trying to construct a large Liquified Natural Gas (LNG) port in the Columbia River Estuary and build 220 miles of high pressure gas pipeline through the Willamette Valley and across the Cascade Mountains? Focus the Nation: Willamette hosts Olivia Schmidt to present an overview about the proposed LNG terminals and pipelines in Oregon, discuss their social and environmental impacts in the Willamette Valley and beyond, and explain the ways that members of the public can take action to protect the Oregon we love from the LNG threat. Please invite your friends and family to learn more about this important and timely issue. For More Information: Sponsored by Other Contact Natalie Sashkin, nsashkin, x503 548 3023 Submitted by nsashkin willamette university campus map ☎ Star 18 20 50 3 TreesStar Trees ☎ ☎ 22 ☎ 7 ☎ 32 12 46 16 40 ☎ 30 8 5 ☎ 37 29 38 Ferry Street ☎ 47 ☎ ☎ 15 Quad ☎ 35 9 ☎ 17 ☎ 10 24 14 43 6 27 42 11 ☎ 26 ☎ 39 ☎ ☎ Permit Parking Lot P 19 r Jackson i n Plaza 14th Street g ☎ ☎ l 21 e P 4 a 49 r k 34 w 33 41 a y ☎ Permit 25 Hatfield Parking Lot Fountain ☎ ☎ ☎ ☎ ☎ 45 ☎ ☎ 1 Permit Sparks Field 44 Permit 36 31 13 2 48 Parking Lot Parking Lot ☎ ☎ 23 Guest Parking Lot ☎ Softball Field ☎ Parking Oak Street Lot Leslie Street Capitol Street University Street Mission Street 28 1 Admission Office (CLA) 18 Gatke Hall 37 Sigma Chi Fraternity 2 Alpha Chi Omega Sorority 19 Goudy Commons 38 Sigma Alpha Epsilon Fraternity 3 Art Building 20 Hallie Ford Museum of Art 39 Smith Auditorium 4 Atkinson Graduate School of Management 21 Mark O.
    [Show full text]
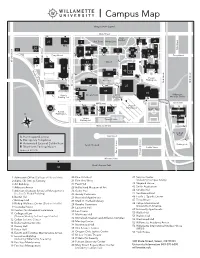
  • Campus Map Front 3-11-15
    Campus Map Oregon State Capitol State Street Rose Garden 23 36 3 Star Trees North Lawn 22 24 34 26 th Street 3 10 12 44 1 53 35 50 15 8 65 33 Ferry Street 51 52 45 Ferry Street Church Street 4 Cottage Street 41 Quad 17 9 29 14 10 19 37 7 31 11 P 21 20 40 r 47 in 16 g 43 le P a r Permit Street k w Mill Race Parking Lot th th Street 2 4 a 25 1 1 y Jackson Winter Street Plaza 27 5 55 39 18 46 Permit Brown Field Hatfield Willamette Parking Lot 30 Fountain Heritage Center Sky Bridge Mill Street Mill Street Permit Parking Lot 49 1 Sparks Field 48 54 Permit 42 38 13 2 Parking Lot 28 Visitor Parking Lot Tennis Courts Bellevue Street Softball Field Handicapped Access Oak Street t Emergency Telephone t Automated External Defibrillator Salem Hospital Parking Lot Short-term Parking Meters Leslie Street Updated: 3/11/15 Capitol Stree University Stree Mission Street Bush’s Pasture Park 32 1 Admission Office (College of Liberal Arts) 20 Fine Arts East 41 Service Center 2 Alpha Chi Omega Sorority 21 Fine Arts West (including Campus Safety) 3 Art Building 22 Ford Hall 42 Shepard House 4 Atkinson Annex 23 Hallie Ford Museum of Art 43 Smith Auditorium 5 Atkinson Graduate School of Management 24 Gatke Hall 44 Smullin Hall (Seeley G. Mudd Building) 25 Goudy Commons 45 Southwood Hall 6 Baxter Hall 26 Haseldorf Apartments 46 Lestle J. Sparks Center 7 Belknap Hall 27 Mark O.
    [Show full text]
  • Oregon Pioneer Wa-Wa: a Compilation of Addresses of Charles B. Moores Relating to Oregon Pioneer History
    OREGON PIONEER WA-WA A COMPILATION OF ADDRESSES OF CHARLES B. MOORES RELATING TO OREGON PIONEER HISTORY PREFACE The within compilation of addresses represents an accumulation of years. Being reluctant to destroy them we are moved for our own personalsatisfaction, to preserve theni in printed form.They contain much that is commonplace, and much that is purely personal and local in character.There is a great surplus of rhetoric. There is possibly an excess of eulogy. There is considerable repetition.There are probably inaccuracies. Thereisnothing, however, included in the compilation that does not have some bearing on Oregon Pioneer History, and this, at least, gives it sonic value.As but a limited nuniber of copies are to be printed, and these arc solely for gratuitous distribution among a few friends, and others, having some interest in the subjects treated, we send the volume adrift, just as it is, without apology and without elimination. Portland, Oregon, March 10, 1923. CHAS. B. MOOnJiS. ADDRESSES Page Chenieketa Lodge No. 1, I. 0. 0. F I Completion of Building of the First M. E. Church of Salem, Oregon 12 Printers' Picnic, Salem, Oregon, 1881 19 Dedication of the Odd Fellows' Temple in Salem, Ore.,190L26 Fiftieth Anniversary Celebration Chemeketa Lodge,I. 0. 0. F. No. 1, Salem, Oregon 34 I)onatjon Land LawFiftieth Anniversary Portland Daily Oregonian 44 Annual Reunion Pioneer Association, Yambill County, Oregon50 Unveiling Marble Tablet, Rev. Alvin F. Wailer 62 Thirty-second Annual Reunion, Oregon State Pioneer Asso- ciation, 1904 69 Laying Cornerstone Eaton Hall, Willarnette University,De- cember 16, 1908 87 Champoeg, May 1911 94 Dedication Jason Lee Memorial Church, Salem, June, 1912 100 Memorial Address, Champocg, Oregon, May 2nd, 1914 107 Oregon M.
    [Show full text]
  • Willamette Campus
    Hallie Ford Museum of Art 700 State Street (1 block west) Graduate School of Education Oregon State Capitol 240 Cottage Street SE (1 block west) Zena Forest, Zena Farm North (8 miles west of Salem on Highway 22, right on North Oak Grove Road) Downtown Salem College of Liberal Arts State Street CAMPUS MAP A Star Trees Ford Gatke C2 Admission Office B3 Matthews Hall Art C2 Alpha Chi Omega Sorority B3 Matthews Academic Center ΦΔΘ (ΑΧΩ) (Learning Center, Writing Center, Bishop Wellness A1 Art Building International Education) Collins Center B1 Atkinson Graduate School A3 Montag Center Olin Science Center of Management A1 Olin Science Center Waller Eaton Smullin Science A3 Phi Delta Theta Fraternity ( ) Center Baxter5 A3 Baxter Hall ΦΔΘ ΣΧ ΣΑΕ B3 Belknap Hall C1 Pi Beta Phi Sorority (ΠΒΦ) B3 Beta Theta Pi Fraternity B2-3 Playhouse and Theatre Walton Montag Center (ΒΘΠ) B2 Putnam University Center Residential A3 Bishop Wellness Center (Bistro, Bookstore, Career Matthews Services (Student Health) Services, Registrar, Financial Aid) Campus Academic ΒΘΠ Safety Quad Center B1 Campus Safety B2 Rogers Music Center (Hudson Concert Hall) Playhouse B1 College of Law A1 Collins Science Center C1 Shepard House Doney Matthews Lausanne C1 Delta Gamma Sorority (ΔΓ) A3 Sigma Chi Fraternity (ΣΧ) Rogers Belknap Terra B1 Doney Hall A3 Sigma Alpha Epsilon Fraternity (ΣΑΕ) Music House B2 Smith Auditorium Center B1 Doney North Offices East A2 Eaton Hall A2-3 Smullin Hall West College of Law Smith Fine Arts B3 Sparks Athletic Center Fine Arts Auditorium B2 Fine
    [Show full text]
  • To Access the David Duniway Papers Finding Aide
    Container List 1999.013 ~ Records ~ Duniway, David C. 07/19/2017 Container Folder Location Creator Date Title Description Subjects Box 01 1.01 1868-1980 Adolph-Gill Bldgs The materials in this folder relate to the buildings owned and occupied by J.K. Gill & Co. and by Sam Adolph. These two buildings are in the heart of the original business district of Salem. The Gill Building (1868) is west of the Adolph Block (1880), and they share a staircase. The Gill building was later referred to as the Paulus Building, as it was acquired by Christopher Paulus in 1885; both Robert and Fred Paulus were born upstairs in the building. The Adolph Building was erected by Sam Adolph following a fire that destroyed the wooden buildings on the site; the architect was J.S. Coulter. References to articles in the Daily American Unionist from April 23, 1868 through September 8, 1868 describe the four new brick buildings under construction on State and Commercial Streets. Thes buildings are the intended new homes for the businesses of J.K. Gill & Co., Charley Stewart, Durbin & Co., and Governor Wood's new dwelling. Progress is periodically described. Finally, the first ten days of September, 1868, the moves appear complete and advertisements indicate the items they will carry. Another article in the September 8, 1868 issue indicates that Story and Thompson are moving a house lately occupied by J.K. Gill and Co. to the eastern edge of the lot so that when it is time to construct additional brick buildings, there will be space.
    [Show full text]
  • WU Campus Map (Pdf)
    A B C D E Oregon State Capitol Zena Forest (8 miles northwest of Salem) Downtown Salem State Street Learning 1 Rose Commons Hallie Oregon Star Trees Garden Ford North Lawn Ford Gatke Civic Justice Art Museum Center University of Art Northwood Services Annex th Street 3 Collins 1 Olin Science Center Smullin Science Waller Eaton Center Global Baxter Learning Southwood Ferry Street Center Walton Ferry Street Cone Montag Service Center Center Chapel Cascadia Church Street Atkinson Cottage Street Campus Safety Westwood Bishop Wellness Annex Doney Quad Center University Willamette M. Lee Services Academy Pelton Matthews College Lausanne Theatre Terra of Law Rogers Belknap Facilities Music Management Center P Smith East r i n West Auditorium Fine Arts g 2 le Fine Arts P a Student/Faculty/Staff r k th Street w Parking Only th Street 4 a 2 1 Mill Stream 1 y Jackson Atkinson Graduate Winter Street Goudy Commons School of Plaza Hatfield Management Renjen Clock Library Center Tower York Putnam University Center Facilities (UC) Sparks Athletic Center Maintenance Hatfield Student/ Willamette Fountain Heritage Center Faculty/Staff Lee Brown Field Parking Only Sky Bridge Admission Office Mill Street Mill Street (Undergraduate) Student/Faculty/Staff Parking Only University Sparks Field Tokyo International Apartments W.I.S.H. Visitor University of America ΠΒΦ ΑΧΩ Parking 3 Student/Faculty/Staff Shepard Kaneko Commons Parking Only Overflow Tennis Courts McCulloch Stadium and athletics complex: Visitor Parking Ogdahl Field (football), John Lewis Field (baseball), Charles Bowles Track (3 blocks south, in Bush’s Pasture Park) Bellevue Street Salem Health Urgent Care B2 Facilities Management D2 Matthews Hall D2 Lestle J.
    [Show full text]
  • College of Law Student Handbook 2019-2020
    2019-2020 COLLEGE OF LAW STUDENT HANDBOOK A B C D E Oregon State Capitol Zena Forest (8 miles northwest of Salem) Downtown Salem State Street Equity & Empowerment Learning Center Rose Commons 1 Hallie Oregon Star Trees Garden Ford Ford Gatke Civic Justice Art North Lawn Museum Center University of Art Northwood Services Annex Bishop Wellness th Street 3 Collins Center 1 Olin Science Center Smullin Willamette Waller Eaton Academy Annex Science Center Global Baxter Learning Southwood Ferry Street Center Walton Ferry Street Cone Montag Chapel Center Church Street Cascadia Atkinson Cottage Street Westwood Annex Doney Quad University M. Lee Services Pelton Matthews College Lausanne Theatre Belknap Terra of Law Rogers Music Service Center Center P Smith East r i Campus Safety n West Auditorium Fine Arts g l Facilities Fine Arts 2 e P Management a r Student/Faculty/Staff k th Street w Parking Only th Street 4 2 a 1 Mill Race 1 y Atkinson Graduate Winter Street Goudy Commons Jackson School of Plaza Hatfield Management Clock Library Tower York Putnam University Center (UC) Facilities Sparks Athletic Center Maintenance Brown Field Hatfield Willamette Student/ Fountain Faculty/Staff Lee Heritage Center Parking Only Sky Bridge Mill Street Mill Street Student/Faculty/Staff Parking Only University Sparks Field Tokyo International Apartments Undergraduate W.I.S.H. Admission Office University of America ΠΒΦ ΔΓ ΑΧΩ willamette.edu/law 3 Student/Faculty/Staff Shepard Kaneko Commons Parking Only Visitor Tennis Courts McCulloch Stadium and athletics complex: Parking Lot Ogdahl Field (football), John Lewis Field (baseball), Charles Bowles Track 503-370-6380 Law Student Affairs (3 blocks south, in Bush’s Pasture Park) Bellevue Street University Information 503-370-6300 245 Winter Street SE, Salem, OR 97301 245 Winter Street B2 Facilities Maintenance B-C3 Lee House D2 Lestle J.
    [Show full text]
  • DRAFT Historical Willamette Documents for Consideration
    DRAFT Historical Willamette Documents for Consideration: CDJS Annual reports and history summary (2006+) During the fall semester of 2006-07, a group of students calling themselves the "Concerned Students for Social Justice" formed, organizing protests on campus and asking the Willamette community to take actions to reaffirm a commitment to values of diversity and social justice. In response to these students' concerns, then-President M. Lee Pelton established the Council on Diversity and Social Justice in November, 2006. Chaired by the university chaplain, Council membership broadly represents the faculty, students, and staff of the university. The charge of the Council, reaffirmed by President Stephen Thorsett, includes diversity of race, ethnicity, culture, gender, religion, national origin, disability, age, sexual orientation, and socio-economic status. Social justice shall be understood as both a process and a goal. "The goal of social justice education is full and equal participation of all groups in a society that is mutually shaped to meet their needs. Social justice includes a vision of society that is equitable and all members are physically and psychologically safe and secure." Since 2006, CDSJ has continued and meets on a regular basis. The Council is chaired by the University Chaplain. CDSJ regularly provides input to the President on social justice matters. CDJS also grants funds to support social justice oriented activities and recently provided feedback on diversity action plans from each Dean. Proposal for Center for Social Justice and Diversity: Concerned Students for Social Justice: 2008 ​ ​ A group of student leaders submitted an extensive report recommending the creation of a Center for Social Justice and Diversity that would serve students, staff and faculty at Willamette.
    [Show full text]