DOCSLIB.ORG

Calibration of the NPTC Range Verifier

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Calibration of the NPTC Range Verifier Calibration of the NPTC range verifier Bernard Gottschalk∗ Harvard Cyclotron Laboratory 44 Oxford St., Cambridge, MA 01238, USA January 16, 2001 Abstract The Range Verifier (RV) is a multi-layer Faraday Cup with relatively thick brass plates. The stopping peak of a monoenergetic proton beam is coarsely binned by the RV so that the main signal appears in only three or four channels. We search for the best way to evaluate this spectrum. Fitting the data with various functions—for instance a Gaussian—works reasonably well, but a straightforward two-step computation of the mean x0 is better and much faster. We study the integral and differential lin- earity of this method using runs at many beam energies, each with several different degrader combinations. We then compare RV measurements with interleaved measurements of the range d80 in a Scanditronix (SCX) water tank. The relation between d80 and x0 requires a small quadratic term because range in brass is not exactly proportional to range in water. The calibration function is x x 2 d =0.0618 + 40.3957 0 +0.9117 0 80 35 35 and agrees with theory. The water tank measurements also yield informa- tion about the difference between d80 and d90 and about the accuracy of the Range at Nozzle Entrance (RNE) set by the NPTC treatment control program. ∗This work was performed for Ion Beam Applications s.a. (IBA). 1 Contents 1 Introduction 3 1.1 The Range Verifier . 3 1.2ErrorinRVData........................... 4 1.3 The Mean Proton Range: r0, d80 and d90 ............. 5 1.4 Equivalent Thicknesses . 5 2 Analysis of the RV Spectrum 7 2.1 Converting to Charge, Merging, Correcting for Beam Steering . 7 2.2 Computing x0 ............................. 7 2.2.1 Fitting the Spectrum . 7 2.2.2 Obtaining x0 Directly.................... 8 3 Results 8 3.1Resolution............................... 9 3.2 RNE-based Runs: Integral and Differential Linearity . 9 3.3 SCX-based Runs: x0 v. Range in Water . 10 3.4 RV Calibration Curve . 10 3.5 d80, d90 andRNE........................... 11 4 Summary and Acknowledgement 11 2 1 Introduction Each proton nozzle of the Northeast Proton Therapy Center (NPTC) includes a Range Verifier (RV) built into one set of jaws of the the variable collimator. This report analyzes recent data taken with the X jaws open and the Y jaws closed (that is, intercepting the full beam) and with nominally monochromatic beams (no depth modulation). We mainly address three questions: • What is the best way to evaluate RV range spectra? • What are the integral linearity, differential linearity and resolution? • How well do RV ranges agree with ranges from Bragg peaks? The remainder of this Introduction, however, is devoted to a brief description of the RV and three related issues: the measurement error in RV data; the definition of mean range and the quantities r0, d80 and d90 and finally, the concept of ‘water equivalent’ and of equivalent thicknesses in general. 1.1 The Range Verifier The RV consists of a Multi-Layer Faraday Cup (MLFC) in each of the two opposing downstream (Y ) jaws of the 4-jaw adjustable collimator, which are ≈ 40 cm downstream of the second scatterer and just upstream of the second ionization chamber set. A MLFC is a stack of metal collecting plates (here 2 mm brass) separated from each other and from ground by thin insulating sheets (here 0.025 mm polyethylene, two thicknesses per gap). Each collector goes to a current integrator. The MLFC has two favorable properties that may not be immediately obvious. First, the ejection of electrons from insulators into collectors and vice versa has no net effect because each such electron remains ‘bound’ to the positive ion it left behind and therefore does not contribute to the measured current. Second, protons that stop in insulators attract a mirror charge into the nearest collector, and are therefore counted just as well as protons that stop in collectors. Therefore the MLFC counts only the incident charge and counts all of it, accurately measuring differential fluence v. depth. The distribution of charge in a MLFC after exposure to monoenergetic pro- tons consists (Fig.1) of a continuum and a sharp peak. The continuum comes from the charged decay products (mostly protons) of the inelastic nuclear inter- actions experienced by some of the incident protons. The peak comes from those protons that stop entirely by electromagnetic interactions. The total charge col- lected equals the beam current entering the device, integrated over time. The continuum can be exactly accounted for by appropriate Monte Carlo models of the nuclear interaction [1]. Note especially that Fig.1 does not look like a Bragg peak and is not a Bragg peak. It is a differential stopping curve, rather than a differential energy deposition curve. For that reason the measured mean proton range corresponds to the peak value rather than the distal 80% value, as will be discussed more fully below. For reasons of economy the present RV is a bit more complicated than a simple stack of collectors. Each of the two jaws has 29 brass plates, each roughly equivalent to 1.1 cm of water. To improve the overall range resolution, one of the jaws has an additional half-thickness plate which is passive (not connected to an integrator). Precise range calculations must also take into account the 2 mm aluminum cover plates, the insulating sheets between the brass plates, and the fact that the brass plates may not have exactly the nominal thickness. If we use the rule (Sec. 1.4) that the effective energy in a finely divided stopping 3 stack is 0.52 × the incident energy, we find that the RV is ≈ 0.4% polyethylene by stopping power. When taking data with monochromatic beams, some upstream scatterer should be used to broaden the beam at the RV so as to reduce the fraction grazing the edge of the plates. In the runs presented below we used at least 1 mm of lead (lollipop #4).1 The transverse proton distribution at the RV can be inferred from the ion chambers downstream of it. The vertical distribution is sharp because the Y jaws are closed, whereas the horizontal distribution reflects the width of the ribbon of beam coming through the small gap between the Y jaws (Fig. 9). Near the maximum energy the distribution at the RV has a FWHM of ≈7 cm for a 1 mm lead scatterer, which appears to be adequate to get a clean spectrum in the RV. 1.2 Error in RV Data Because raw RV numbers are usually referred to as ‘counts’ and because of the superficial resemblance between an RV spectrum and a pulse height or Monte Carlo spectrum, there is an erroneous tendency to think of the error of each RV datum as having something to do with the square root of the number. Actually the error is far smaller. Each RV channel represents a charge measurement, not a statistical sample. The error comes from the resolution of the measurement, ∆Q = 10 pC, and is constant, independent of the ‘counts’. This is illustrated by Fig. 2, where a portion of the spectrum is shown for seven runs taken back- to-back. Because the count interval varied a bit (no beam monitor), the spectra have been normalized to the same total charge. Even the funny-looking peak channel (≈ 260 ‘counts’) has an rms spread√ of only 0.6%. If this were a statistical sample the relative error would be 1/ 260 or about 6%! The expected order of magnitude of the error is easily found. A recycling integrator with its counter is equivalent to an analog-to-digital converter having charge resolution ∆Q. The measured charge Q0 always equals ∆Q times an integer e.g. 1.000 nC for 100 counts. Only the counter, not the residual charge, is reset at the beginning of a measurement. The true charge Q that came in during the measurement interval may be nearly ∆Q less than Q0 (if the residual charge was nearly ∆Q) or it may be nearly ∆Q more (if the residual charge was nearly 0). Therefore the measurement error Q − Q0 is uniformly distributed between −∆Q and +∆Q if we assume all values of residual charge are equally likely. The rms error is therefore√ the rms deviation of a square distribution of half-width ∆Q, namely ∆Q/ 3 ≈ 0.6∆Q. Of course it is frequently the case that not all values of residual charge are equally likely. The runs may be taken back-to-back as here, leading to correlations. The measured rms deviation for all active channels in Fig. 2 varies considerably but averages only 0.4∆Q. However, without belaboring the point further we may conclude that the error in any point is at most a fraction of a count. Therefore a hundred counts or so in the peak channel is generally enough for a good measurement. That corresponds to a nanoAmp for a few seconds if the RV intercepts most of the beam. Under those circumstance the overall error in the range determination probably depends more on the algorithm used to find the range than on the number of counts, as will be seen below. 1A ‘lollipop’, so called because of its shape, is one of six lead or three Lexan degraders that may be inserted into the beam just upstream of the range modulator. 4 1.3 The Mean Proton Range: r0, d80 and d90 The distal 80% point d80 and the distal 90% point d90 of the Bragg peak are both relevant to proton radiation therapy, leading to potential confusion and annoyance.
Load more

Recommended publications
  • Proposed Method for Measuring the LET of Radiotherapeutic Particle Beams Stephen D
    University of New Mexico UNM Digital Repository Physics & Astronomy ETDs Electronic Theses and Dissertations Fall 11-10-2017 Proposed Method for Measuring the LET of Radiotherapeutic Particle Beams Stephen D. Bello University of New Mexico - Main Campus Follow this and additional works at: https://digitalrepository.unm.edu/phyc_etds Part of the Astrophysics and Astronomy Commons, Health and Medical Physics Commons, Other Medical Sciences Commons, and the Other Physics Commons Recommended Citation Bello, Stephen D.. "Proposed Method for Measuring the LET of Radiotherapeutic Particle Beams." (2017). https://digitalrepository.unm.edu/phyc_etds/167 This Dissertation is brought to you for free and open access by the Electronic Theses and Dissertations at UNM Digital Repository. It has been accepted for inclusion in Physics & Astronomy ETDs by an authorized administrator of UNM Digital Repository. For more information, please contact [email protected]. Dedication To my father, who started my interest in physics, and my mother, who encouraged me to expand my mind. iii Acknowledgments I’d like to thank my advisor, Dr. Michael Holzscheiter, for his endless support, as well as putting up with my relentless grammatical errors concerning the focus of our research. And Dr. Shuang Luan for his feedback and criticism. iv Proposed Method for Measuring the LET of Radiotherapeutic Particle Beams by Stephen Donald Bello B.S., Physics & Astronomy, Ohio State University, 2012 M.S., Physics, University of New Mexico, 2017 Ph.D, Physics, University of New Mexico, 2017 Abstract The Bragg peak geometry of the depth dose distributions for hadrons allows for precise and e↵ective dose delivery to tumors while sparing neighboring healthy tis- sue.
    [Show full text]
  • Radiation Therapy
    Radiation Therapy Use of radiation to kill diseased cells. Cancer is the disease that is almost always treated when using radiation. • One person in three will develop some form of cancer in their lifetime. • One person in five will die from that cancer. • Cancer is the second leading cause of death but exceeds all other diseases in terms of years of working-life lost. Diagrammatic representation of a Image removed. slice through a large solid tumor. From Webster’s Medical Dictionary: Cancer – A malignant tumor of potentially unlimited growth that expands locally by invasion and sytemically by metastasis. Tumor – an abnormal mass of tissues that arises from cells of pre-existent tissue, and serves no useful purpose. Malignant – dangerous and likely to be fatal (as opposed to “benign,” which refers to a non-dangerous growth). 1 Unlimited Growth: • Cancer cells multiply in an unregulated manner independent of normal control mechanisms. • Formation of a solid mass in organs. • Multiplication of bone marrow stem cells gives rise to leukemia, a cancer of the blood. Image removed. Solid tumors: • Primary tumor may be present in the body for months or years before clinical symptoms develop. • Some tumors can be managed and the patient often cured provided there has been no significant invasion of vital organs. • Patients do not often die of primary tumors---brain tumors are the exception. Metastases: • The spread of tumor cells from one part of the body to another, usually by the blood or lymph systems. • Metastases are more usually the cause of death. • Metastases are especially common in the bone marrow, liver, lungs and brain.
    [Show full text]
  • Ionoacoustic Bragg Peak Localization for Charged Particle Cancer Therapy
    Ionoacoustic Bragg Peak Localization for Charged Particle Cancer Therapy Siavash Yousefi, December-9-2015 Jonathan Alava, 7 Roberts Proton Therapy Center in Philadelphia Cancer Treatment: Protons vs. X-ray Superior Dose Distribution Photon vs. Proton Dose Distribution http://www.wikiwand.com/en/Particle_therapy Knopf, Antje-Christin, and Antony Lomax. "In vivo proton range verification: a review." Physics in medicine and biology 58.15 (2013): R131. Proton and Carbon Therapy Facilities Carbon Therapy Facilities PROTON THERAPY FACILITIES External Beam LINAC External Beam LINAC Proton Therapy Facility : C Heidelberg Ion Therapy Center 60m x 70m Compact Design Uncertainties in Proton Therapy • Due to sharp dose fall-off at Bragg peak • Protons are more sensitive to uncertainties than photon • Damaging surrounding healthy tissue/not treating tumor Sources of uncertainties • Stochastic error (CT noise) • CT artifacts • CT resolution (partial volume effect) • Hounsfield unit (HU) conversion method Proton Range Verification Techniques Measurement technique › Direct › Indirect: range is implied from another signal Timing › Online: during treatment delivery › Offline: performed after completion of the treatment Direct Indirect Prompt gamma imaging (3D) Range probes PET imaging (3D) Online Proton radiography Ionoacoustic PET imaging (3D) Offline MRI (3D) PET Imaging for Range Verification • Protons and heavy ions cause nuclear fragmentation reactions • Generation of positron emitting isotopes (15O, 11C) • PET scan measures the distribution of activities • Clinically appealing; no additional dose to the patient PET Verification of Proton Therapy: Operational Modalities In-beam PET Offline PET In-room PET PET Verification Studies in Patient Clival chordoma receiving a posterior–anterior followed by a lateral field ~26 min (T1) and 16 min (T2) after completion.
    [Show full text]
  • Stereotactic Radiosurgery with Charged-Particle Beams: Technique and Clinical Experience
    Review Article Stereotactic radiosurgery with charged-particle beams: technique and clinical experience Richard P. Levy1, Reinhard W. M. Schulte2 1Advanced Beam Cancer Treatment Foundation, 887 Wildrose Circle, Lake Arrowhead, CA 92352-2356 USA; 2Department of Radiation Medicine, Loma Linda University Medical Center, Loma Linda, CA, 92354, USA Corresponding to: Richard Levy, MD, PhD. PO Box 2356, Lake Arrowhead, CA 92352-2356 USA. Email: [email protected]. Abstract: Stereotactic radiosurgery using charged-particle beams has been the subject of biomedical research and clinical development for almost 60 years. Energetic beams of charged particles of proton mass or greater (e.g., nuclei of hydrogen, helium or carbon atoms) manifest unique physical and radiobiological properties that offer advantages for neurosurgical application and for neuroscience research. These beams can be readily collimated to any desired cross-sectional size and shape. At higher kinetic energies, the beams can penetrate entirely through the patient in a similar fashion to high-energy photon beams but without exponential fall-off of dose. At lower kinetic energies, the beams exhibit increased dose-deposition (Bragg ionization peak) at a finite depth in tissue that is determined by the beam’s energy as it enters the patient. These properties enable highly precise, 3-dimensional placement of radiation doses to conform to uniquely shaped target volumes anywhere within the brain. Given the radiosurgical requirements for diagnostic image acquisition and fusion, precise target delineation and treatment planning, and millimeter- or even submillimeter-accurate dose delivery, reliable stereotactic fixation and immobilization techniques have been mandatory for intracranial charged particle radiosurgery. Non-invasive approaches initially used thermoplastic masks with coordinate registration made by reference to bony landmarks, a technique later supplemented by using vacuum-assisted dental fixation and implanted titanium fiducial markers for image guidance.
    [Show full text]
  • Dose Reporting in Ion Beam Therapy
    IAEA-TECDOC-1560 Dose Reporting in Ion Beam Therapy Proceedings of a meeting organized jointly by the International Atomic Energy Agency and the International Commission on Radiation Units and Measurements, Inc. and held in Ohio, United States of America, 18–20 March 2006 June 2007 IAEA-TECDOC-1560 Dose Reporting in Ion Beam Therapy Proceedings of a meeting organized jointly by the International Atomic Energy Agency and the International Commission on Radiation Units and Measurements, Inc. and held in Ohio, United States of America, 18–20 March 2006 June 2007 The originating Section of this publication in the IAEA was: Applied Radiation Biology and Radiotherapy Section International Atomic Energy Agency Wagramer Strasse 5 P.O. Box 100 A-1400 Vienna, Austria DOSE REPORTING IN ION BEAM THERAPY IAEA, VIENNA, 2007 IAEA-TECDOC-1560 ISBN 978–92–0–105807–2 ISSN 1011–4289 © IAEA, 2007 Printed by the IAEA in Austria June 2007 FOREWORD Following the pioneering work in Berkeley, USA, ion beam therapy for cancer treatment is at present offered in Chiba and Hyogo in Japan, and Darmstadt in Germany. Other facilities are coming close to completion or are at various stages of planning in Europe and Japan. In all these facilities, carbon ions have been selected as the ions of choice, at least in the first phase. Taking into account this fast development, the complicated technical and radiobiological research issues involved, and the hope it raises for some types of cancer patients, the IAEA and the International Commission on Radiation Units and measurements (ICRU) jointly sponsored a technical meeting held in Vienna, 23–24 June 2004.
    [Show full text]
  • Α-Particle Emitters in Radioimmunotherapy: New And
    INVITED COMMENTARY ␣-Particle Emitters in Radioimmunotherapy: New and Welcome Challenges to Medical Internal Dosimetry sulting in the release of the daughter as the cellular S value methodology to Over the past decade, there has a free element. include time-dependent partial contri- been progressively stronger interest in Two very different approaches can butions of the various daughter emis- the use of ␣-particle emitters for radio- be applied to the dosimetry of ␣-parti- sions in the serial decay chains of immunotherapy (1–6). With proper lo- cle emitters. One is microdosimetry, in 225Ac, 221At, 213Bi, and 223Ra. In their calization of the labeled antibody, the which the probabilistic nature of approach, a cutoff time (␶0) is selected high linear energy transfer of ␣-parti- ␣-particle emission and its trajectory before which free elemental daughter cles provides a correspondingly high through the cell and cell nucleus are radionuclides are considered to remain probability of mitotic cell kill when explicitly considered (1,8–10). In a in the same source configuration as compared with an equivalent number microdosimetric analysis, probability that assumed for the parent. At short of cellular traversals by lower linear density functions of specific energy are cutoff times, the daughter radionu- energy transfer ␤-particles. Conse- obtained (stochastic expressions of en- clides, which are released as free ele- quently, much developmental work ergy imparted per unit mass to small ments after the ␣-decay of the parent, has been initiated in the production, targets), as well as frequencies of zero- diffuse or migrate far from the site of chemistry, and preclinical trials of can- dose contribution.
    [Show full text]
  • Basic Physics of Proton Therapy
    University of Florida Proton Therapy Institute Basic Physics of Proton Therapy Roelf Slopema overview I. basic interactions . energy loss . scattering . nuclear interactions II. clinical beams . pdd . lateral penumbra interactions / energy loss Primarily protons lose energy in coulomb interactions with the outer-shell electrons of the target atoms. • excitation and ionization of atoms • loss per interaction small ‘continuously slowing down’ • range secondary e+ <1mm dose absorbed locally • no significant deflection protons by electrons interactions / energy loss Energ y loss is given b y Bethe-Bloch equ ation: + corrections Tmax max energy transfer to free electron Tmax max energy transfer to free electron • to first order: –dE/dx 1/speed2 2 2 • max electron energy: Tmax 4Tm4 T mec /m/ mpc T=200 MeV Tmax 0.4 MeV range 1.4mm ….but most electrons far lower energy in practice we use range-energy tables and measured depth dose curves. Equations from Review of particle physics, C. Amsler et al., Physics Letters B667, 1 (2008) stopping power water stopping power water p+ 200MeV Bragg peak Bragg peak Bragg peak William Bragg W.H. Bragg and R. Kleeman, On the ionization curves of radium, Philosophical Magazine S6 (1904), 726-738 stopping power Graph based on NIST data interactions / scattering PiPrimaril y protons scatter d ue to el asti c coulomb interactions with the target nuclei. • many, small angle deflections • full description Moliere, gaussian approx. Highland p proton momentum L target thickness v proton speed LR target radiation length . 0 1/pv 1/(2*T) T<<938MeV -050.5 . material dependence: 0 1/LR 2 2 1 g/cm of water (LR =36.1 g/cm ) 0=5mrad for T=200MeV 2 2 1 g/cm of lead (LR = 6.37 g/cm ) 0=14mrad for T=200MeV Highland neglects large-angle tails, but works well in many situations… Equation from Gottschalk (Passive beam spreading) radial spread in water Approximation: 0.02 x range Calculation using Highland’s equation.
    [Show full text]
  • Penetration of Proton Beams Through Water 1. Depth-Dose Distribution
    NISTIR 5226 Penetration of Proton Beams Through Water I. Depth-dose Distribution, Spectra and LET Distribution Martin J. Berger U.S. DEPARTMENT OF COMMERCE Technology Administration National Institute of Standards and Technology Physics Laboratory Ionizing Radiation Division Gaithersburg, MD 20899 Prepared for: National Cancer Institute Bethesda, MD 20892 100 .056 NIST #5226 1S95 NISTIR 5226 Penetration of Proton Beams Through Water I. Depth-dose Distribution, Spectra and LET Distribution Martin J. Berger DATE DUE Mia 2 2( O3 5 7"f0:^ \(p1X\ U.S. DEPARTMENT OF COMMERCE Technology Administration National Institute of Standards and Technology Physics Laboratory Ionizing Radiation Division Gaithersburg, MD 20899 Prepared for: National Cancer Institute Bethesda, MD 20892 July 1993 GAYLORD PRINTED IN U.S.A. U.S. DEPARTMENT OF COMMERCE Ronald H. Brown, Secretary NATIONAL INSTITLITE OF STANDARDS AND TECHNOLOGY Arati Prabhakar, Director Penetration of Proton Becuns Through Water I. Depth-dose Distributions, Spectra and LET Distributions Martin J. Berger* Physics Laboratory** National Institute of Standards and Technology Gaithersburg, MD 20899 The penetration of protons through a water phantom was calculated with the Monte Carlo program PTRAN, which takes into account energy-loss straggling, multiple scattering, and nonelastic nuclear interactions. Calculations were done for incident proton beams incident with energies between 250 MeV and 50 MeV. The information obtained includes depth- dose curves as well as energy spectra of primary protons at various depth Good agreement was found between calculated and measured relative depth- dose distributions, except at extreme depths. A systematic tabulation was made of various parameters that characterize the shape of the Bragg peak.
    [Show full text]
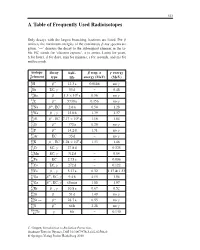
  • A Table of Frequently Used Radioisotopes
    323 A Table of Frequently Used Radioisotopes Only decays with the largest branching fractions are listed. For β emitters the maximum energies of the continuous β-ray spectra are given. ‘→’ denotes the decay to the subsequent element in the ta- ble. EC stands for ‘electron capture’, a (= annus, Latin) for years, h for hours, d for days, min for minutes, s for seconds, and ms for milliseconds. isotope decay half- β resp. α γ energy A Z element type life energy (MeV) (MeV) 3 β− . γ 1H 12 3a 0.0186 no 7 γ 4Be EC, 53 d – 0.48 10 β− . × 6 γ 4Be 1 5 10 a 0.56 no 14 β− γ 6C 5730 a 0.156 no 22 β+ . 11Na ,EC 2 6a 0.54 1.28 24 β− γ . 11Na , 15 0h 1.39 1.37 26 β+ . × 5 13Al ,EC 7 17 10 a 1.16 1.84 32 β− γ 14Si 172 a 0.20 no 32 β− . γ 15P 14 2d 1.71 no 37 γ 18Ar EC 35 d – no 40 β− . × 9 19K ,EC 1 28 10 a 1.33 1.46 51 γ . 24Cr EC, 27 8d – 0.325 54 γ 25Mn EC, 312 d – 0.84 55 . 26Fe EC 2 73 a – 0.006 57 γ 27Co EC, 272 d – 0.122 60 β− γ . 27Co , 5 27 a 0.32 1.17 & 1.33 66 β+ γ . 31Ga , EC, 9 4h 4.15 1.04 68 β− γ 31Ga , EC, 68 min 1.88 1.07 85 β− γ .
    [Show full text]
  • Proton Therapy
    Proton Beam Radiotherapy - The State of the Art1 Harald Paganetti and Thomas Bortfeld Massachusetts General Hospital, Boston, MA, USA 1. Introduction a - Physical Rationale Protons have different dosimetric characteristics than photons used in conventional radiation therapy. After a short build-up region, conventional radiation shows an exponentially decreasing energy deposition with increasing depth in tissue. In contrast, protons show an increasing energy deposition with penetration distance leading to a maximum (the “Bragg peak”) near the end of range of the proton beam (figure 1). 120 100 80 ] 60 Dose [% 40 20 0 0 50 100 150 200 250 300 depth [mm] Figure 1: Typical dose deposition as a function of depth for a proton beam. Protons moving through tissue slow down loosing energy in atomic or nuclear interaction events. This reduces the energy of the protons, which in turn causes increased interaction with orbiting electrons. Maximum interaction with electrons occurs at the end of range causing maximum energy release within the targeted area. This physical characteristic of protons causes an advantage of proton treatment over conventional radiation because the region of maximum energy deposition can be 1 To be published in: New Technologies in Radiation Oncology (Medical Radiology Series) (Eds.) W. Schlegel, T. Bortfeld and A.-L. Grosu Springer Verlag, Heidelberg, ISBN 3-540-00321-5, October 2005 Paganetti & Bortfeld: Proton Beam Radiotherapy positioned within the target for each beam direction. This creates a highly conformal high dose region, e.g., created by a spread-out Bragg peak (SOBP) (see section 3a), with the possibility of covering the tumor volume with high accuracy.
    [Show full text]
  • Proton and Heavy Particle Intracranial Radiosurgery
    biomedicines Review Proton and Heavy Particle Intracranial Radiosurgery Eric J. Lehrer 1, Arpan V. Prabhu 2 , Kunal K. Sindhu 1 , Stanislav Lazarev 1, Henry Ruiz-Garcia 3, Jennifer L. Peterson 3, Chris Beltran 3, Keith Furutani 3, David Schlesinger 4, Jason P. Sheehan 4 and Daniel M. Trifiletti 3,* 1 Department of Radiation Oncology, Icahn School of Medicine at Mount Sinai, New York, NY 10029, USA; [email protected] (E.J.L.); [email protected] (K.K.S.); [email protected] (S.L.) 2 Department of Radiation Oncology, UAMS Winthrop P. Rockefeller Cancer Institute University of Arkansas for Medical Sciences, Little Rock, AR 72205, USA; [email protected] 3 Department of Radiation Oncology, Mayo Clinic, Jacksonville, FL 32224, USA; [email protected] (H.R.-G.); [email protected] (J.L.P.); [email protected] (C.B.); [email protected] (K.F.) 4 Department of Neurological Surgery, University of Virginia, Charlottesville, VA 22903, USA; [email protected] (D.S.); [email protected] (J.P.S.) * Correspondence: Trifi[email protected]; Tel.: +1-904-953-1000 Abstract: Stereotactic radiosurgery (SRS) involves the delivery of a highly conformal ablative dose of radiation to both benign and malignant targets. This has traditionally been accomplished in a single fraction; however, fractionated approaches involving five or fewer treatments have been delivered for larger lesions, as well as lesions in close proximity to radiosensitive structures. The clinical utilization of SRS has overwhelmingly involved photon-based sources via dedicated radiosurgery ® ® platforms (e.g., Gamma Knife and Cyberknife ) or specialized linear accelerators.
    [Show full text]
  • Bragg Peak Flattening Filter for Dose Delivery Utilizing Energy Stacking Region (Fujitaka, Takayanagi, Fujimoto, Fujii, 1' G
    PHYSICS Bragg Peak Flattening Filter for Dose Delivery Utilizing Energy Stacking region (Fujitaka, Takayanagi, Fujimoto, Fujii, 1' G. Warrell Terunuma 3101 ; Weber, Kraft 2765). Abstract Previous ripple filters have either used multiple Proton beam radiotherapy is attractive for cancer treatment because of the unusually sharp Bragg simply consisted of single sheets of material wit peak exhibited by proton beams. However, many beam energies are needed to cover the entire thicknesses (Fujitaka, Takayanagi, Fujimoto, Fr volume of the tumor, increasing the sensitivity of the treatment to target motion. It is therefore Terunuma 3 JO I ; Weber, Kraft 2767). The goal ' desirable to have a flattening filter that necessitates fewer beam energies to cover the target by single-layer flattening filter, consisting of an ak spreading out the Bragg peak. A prototype aluminum grid flattening filter was designed, proton Bragg peak in a clinically useful way. Tl manufactured, and tested at the Indiana University Cyclotron Facility (IUCF). It has been found the Indiana University Cyclotron Facility (IUCI feasible to use such a filter to treat the patient with fewer beam energies. However, further work is necessary to generate a sufficiently uniform dose for clinical purposes. Materials and Methods Introduction Aluminum, an easily machined material with a 1 filter in order to minimize the lateral scattering' obert Wilson initially proposed proton radiotherapy for cancer treatment in his seminal for manufacturing the flattening filter had a thic 1946 paper, Radiological Use of Fast Protons (Wilson 487). Since then, twenty-six clinical first step in designing the prototype flattening fi R find the proper weighting factor, defined as the proton therapy facilities have been built worldwide, and nearly as many are planned to be built (Kraft 1083).
    [Show full text]