Liouville's Theorem on Integration in Terms of Elementary Functions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Elementary Functions: Towards Automatically Generated, Efficient
Elementary functions : towards automatically generated, efficient, and vectorizable implementations Hugues De Lassus Saint-Genies To cite this version: Hugues De Lassus Saint-Genies. Elementary functions : towards automatically generated, efficient, and vectorizable implementations. Other [cs.OH]. Université de Perpignan, 2018. English. NNT : 2018PERP0010. tel-01841424 HAL Id: tel-01841424 https://tel.archives-ouvertes.fr/tel-01841424 Submitted on 17 Jul 2018 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Délivré par l’Université de Perpignan Via Domitia Préparée au sein de l’école doctorale 305 – Énergie et Environnement Et de l’unité de recherche DALI – LIRMM – CNRS UMR 5506 Spécialité: Informatique Présentée par Hugues de Lassus Saint-Geniès [email protected] Elementary functions: towards automatically generated, efficient, and vectorizable implementations Version soumise aux rapporteurs. Jury composé de : M. Florent de Dinechin Pr. INSA Lyon Rapporteur Mme Fabienne Jézéquel MC, HDR UParis 2 Rapporteur M. Marc Daumas Pr. UPVD Examinateur M. Lionel Lacassagne Pr. UParis 6 Examinateur M. Daniel Menard Pr. INSA Rennes Examinateur M. Éric Petit Ph.D. Intel Examinateur M. David Defour MC, HDR UPVD Directeur M. Guillaume Revy MC UPVD Codirecteur À la mémoire de ma grand-mère Françoise Lapergue et de Jos Perrot, marin-pêcheur bigouden. -

What Is a Closed-Form Number? Timothy Y. Chow the American
What is a Closed-Form Number? Timothy Y. Chow The American Mathematical Monthly, Vol. 106, No. 5. (May, 1999), pp. 440-448. Stable URL: http://links.jstor.org/sici?sici=0002-9890%28199905%29106%3A5%3C440%3AWIACN%3E2.0.CO%3B2-6 The American Mathematical Monthly is currently published by Mathematical Association of America. Your use of the JSTOR archive indicates your acceptance of JSTOR's Terms and Conditions of Use, available at http://www.jstor.org/about/terms.html. JSTOR's Terms and Conditions of Use provides, in part, that unless you have obtained prior permission, you may not download an entire issue of a journal or multiple copies of articles, and you may use content in the JSTOR archive only for your personal, non-commercial use. Please contact the publisher regarding any further use of this work. Publisher contact information may be obtained at http://www.jstor.org/journals/maa.html. Each copy of any part of a JSTOR transmission must contain the same copyright notice that appears on the screen or printed page of such transmission. JSTOR is an independent not-for-profit organization dedicated to and preserving a digital archive of scholarly journals. For more information regarding JSTOR, please contact [email protected]. http://www.jstor.org Mon May 14 16:45:04 2007 What Is a Closed-Form Number? Timothy Y. Chow 1. INTRODUCTION. When I was a high-school student, I liked giving exact answers to numerical problems whenever possible. If the answer to a problem were 2/7 or n-6 or arctan 3 or el/" I would always leave it in that form instead of giving a decimal approximation. -

Elementary Functions and Their Inverses*
ELEMENTARYFUNCTIONS AND THEIR INVERSES* BY J. F. RITT The chief item of this paper is the determination of all elementary functions whose inverses are elementary. The elementary functions are understood here to be those which are obtained in a finite number of steps by performing algebraic operations and taking exponentials and logarithms. For instance, the function tan \cf — log,(l + Vz)] + [«*+ log arc sin*]1« is elementary. We prove that if F(z) and its inverse are both elementary, there exist n functions Vt(*)j <hiz), •', <Pniz), where each <piz) with an odd index is algebraic, and each (p(z) with an even index is either e? or log?, such that F(g) = <pn(pn-f-<Pn9i(z) each q>i(z)ii<ît) being substituted for z in ^>iiiz). That every F(z) of this type has an elementary inverse is obvious. It remains to develop a method for recognizing whether a given elementary function can be reduced to the above form for F(.z). How to test fairly simple functions will be evident from the details of our proofs. For the immediate present, we let the general question stand. The present paper is an addition to Liouville's work of almost a century ago on the classification of the elementary functions, on the possibility of effecting integrations in finite terms, and on the impossibility of solving certain differentia] equations, and certain transcendental equations, in finite terms.!" Free use is made here of the ingenious methods of Liouville. * Presented to the Society, October 25, 1924. -(•Journal de l'Ecole Polytechnique, vol. -
![Arxiv:1911.10319V2 [Math.CA] 29 Dec 2019 Roswl Egvni H Etscin.Atraiey Ecnuse Can We Alternatively, Sections](https://docslib.b-cdn.net/cover/9632/arxiv-1911-10319v2-math-ca-29-dec-2019-roswl-egvni-h-etscin-atraiey-ecnuse-can-we-alternatively-sections-1059632.webp)
Arxiv:1911.10319V2 [Math.CA] 29 Dec 2019 Roswl Egvni H Etscin.Atraiey Ecnuse Can We Alternatively, Sections
Elementary hypergeometric functions, Heun functions, and moments of MKZ operators Ana-Maria Acu1a, Ioan Rasab aLucian Blaga University of Sibiu, Department of Mathematics and Informatics, Str. Dr. I. Ratiu, No.5-7, RO-550012 Sibiu, Romania, e-mail: [email protected] bTechnical University of Cluj-Napoca, Faculty of Automation and Computer Science, Department of Mathematics, Str. Memorandumului nr. 28 Cluj-Napoca, Romania, e-mail: [email protected] Abstract We consider some hypergeometric functions and prove that they are elementary functions. Con- sequently, the second order moments of Meyer-K¨onig and Zeller type operators are elementary functions. The higher order moments of these operators are expressed in terms of elementary func- tions and polylogarithms. Other applications are concerned with the expansion of certain Heun functions in series or finite sums of elementary hypergeometric functions. Keywords: hypergeometric functions, elementary functions, Meyer-K¨onig and Zeller type operators, polylogarithms; Heun functions 2010 MSC: 33C05, 33C90, 33E30, 41A36 1. Introduction This paper is devoted to some families of elementary hypergeometric functions, with applica- tions to the moments of Meyer-K¨onig and Zeller type operators and to the expansion of certain Heun functions in series or finite sums of elementary hypergeometric functions. In [4], J.A.H. Alkemade proved that the second order moment of the Meyer-K¨onig and Zeller operators can be expressed as 2 2 x(1 − x) Mn(e2; x)= x + 2F1(1, 2; n + 2; x), x ∈ [0, 1). (1.1) arXiv:1911.10319v2 [math.CA] 29 Dec 2019 n +1 r Here er(t) := t , t ∈ [0, 1], r ≥ 0, and 2F1(a,b; c; x) denotes the hypergeometric function. -

The Mathematical-Function Computation Handbook Nelson H.F
The Mathematical-Function Computation Handbook Nelson H.F. Beebe The Mathematical-Function Computation Handbook Programming Using the MathCW Portable Software Library Nelson H.F. Beebe Department of Mathematics University of Utah Salt Lake City, UT USA ISBN 978-3-319-64109-6 ISBN 978-3-319-64110-2 (eBook) DOI 10.1007/978-3-319-64110-2 Library of Congress Control Number: 2017947446 © Springer International Publishing AG 2017 This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed. The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use. The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the publisher nor the authors or the editors give a warranty, express or implied, with respect to the material contained herein or for any errors or omissions that may have been made. The publisher remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. Printed on acid-free paper This Springer imprint is published by Springer Nature The registered company is Springer International Publishing AG The registered company address is: Gewerbestrasse 11, 6330 Cham, Switzerland Dedication This book and its software are dedicated to three Williams: Cody, Kahan, and Waite. -

INTEGRATION STRATEGIES 1. Introduction It Should Be Clear Now
INTEGRATION STRATEGIES 1. Introduction It should be clear now that it is a whole lot easier to differentiate a function than integrating one. Typically the formula used to determine the derivative of a function is apparent. With integration, the appropriate formula won't necessarily be obvious. So far we have reviewed each of the basic techniques of integration: with substitutions (ch. 5.5, 7.2, 7.3 ), integration by parts (ch. 7.1), and partial fractions (ch 7.4). More realistically, integrals will be given outside of the context of a textbook chapter and the challenge is to identify which formula(s) to use. We will review several integrals at random and suggest strategies for determining which formula to evaluate the integral. These strategies will only be helpful if one has a knowledge of basic integration formulas. Listed in the table below are an expanded list of the formulas for commonly used integrals. Many of these can be derived using basic principles it will be helpful to memorize these. In lieu of formulas 19 and 20 one could use partial fractions and trigonometric substitutions respectively. Figure 1. Table of Integration Formulas Constant of integra- tion have been omitted. 1 2 INTEGRATION STRATEGIES 2. Strategies If an integral does not fit into this basic list of integration formulas, try the following strategy: (1) Simplify the Integrand if Possible: Algebraic manipulation or trigono- metric identities can simplify the integrand and allow for integration in its new form. For example, p p p R x(1 + x)dx = R ( x + x)dx; R tan θ R sin θ 2 R R sec2 θ dθ = cos θ cos θdθ = sin θ cos θdθ = frac12 sin 2θdθ; R (sin x + cos x)2dx = R (sin2 x + 2 sin x cos x + cos2 x)dx = R (1 + 2 sin x cos x)dx; (2) Look for an Obvious Substitution: Try substitutions u = g(x) in the integrand for which the differential du = g0(x)dx also appears in the integran. -

Elementary Functions and Approximate Computing Jean-Michel Muller
Elementary Functions and Approximate Computing Jean-Michel Muller To cite this version: Jean-Michel Muller. Elementary Functions and Approximate Computing. Proceedings of the IEEE, Institute of Electrical and Electronics Engineers, 2020, 108 (12), pp.1558-2256. 10.1109/JPROC.2020.2991885. hal-02517784v2 HAL Id: hal-02517784 https://hal.archives-ouvertes.fr/hal-02517784v2 Submitted on 29 Apr 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. 1 Elementary Functions and Approximate Computing Jean-Michel Muller** Univ Lyon, CNRS, ENS de Lyon, Inria, Université Claude Bernard Lyon 1, LIP UMR 5668, F-69007 Lyon, France Abstract—We review some of the classical methods used for consequence of that nonlinearity is that a small input error quickly obtaining low-precision approximations to the elementary can sometimes imply a large output error. Hence a very careful functions. Then, for each of the three main classes of elementary error control is necessary, especially when approximations are function algorithms (shift-and-add algorithms, polynomial or rational approximations, table-based methods) and for the ad- cascaded: approximate computing cannot be quick and dirty y y log (x) ditional, specific to approximate computing, “bit-manipulation” computing. -

Antiderivatives Basic Integration Formulas Structural Type Formulas
Antiderivatives Definition 1 (Antiderivative). If F 0(x) = f(x) we call F an antideriv- ative of f. Definition 2 (Indefinite Integral). If F is an antiderivative of f, then R f(x) dx = F (x) + c is called the (general) Indefinite Integral of f, where c is an arbitrary constant. The indefinite integral of a function represents every possible antideriv- ative, since it has been shown that if two functions have the same de- rivative on an interval then they differ by a constant on that interval. Terminology: When we write R f(x) dx, f(x) is referred to as the in- tegrand. Basic Integration Formulas As with differentiation, there are two types of formulas, formulas for the integrals of specific functions and structural type formulas. Each formula for the derivative of a specific function corresponds to a formula for the derivative of an elementary function. The following table lists integration formulas side by side with the corresponding differentiation formulas. Z xn+1 d xn dx = if n 6= −1 (xn) = nxn−1 n + 1 dx Z d sin x dx = − cos x + c (cos x) = − sin x dx Z d cos x dx = sin x + c (sin x) = cos x dx Z d sec2 x dx = tan x + c (tan x) = sec2 x dx Z d ex dx = ex + c (ex) = ex dx Z 1 d 1 dx = ln x + c (ln x) = x dx x Z d k dx = kx + c (kx) = k dx Structural Type Formulas We may integrate term-by-term: R kf(x) dx = k R f(x) dx 1 2 R f(x) ± g(x) dx = R f(x) dx ± R g(x) dx In plain language, the integral of a constant times a function equals the constant times the derivative of the function and the derivative of a sum or difference is equal to the sum or difference of the derivatives. -
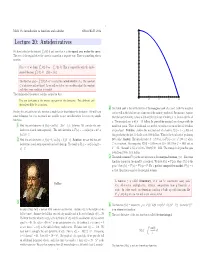
Lecture 20: Antiderivatives 15 X We Have Looked at the Integral 0 F(T) Dt and Seen That It Is the Signed Area Under the Curve
2 Math 1A: introduction to functions and calculus Oliver Knill, 2012 20 Lecture 20: Antiderivatives 15 x We have looked at the integral 0 f(t) dt and seen that it is the signed area under the curve. The area of the region below theR curve is counted in a negative way. There is something else to mention: 10 0 x For x< 0, we define x f(t) dt as 0 f(t) dt. This is compatible with the funda- b ′ R − R mental theorem a f (t) dt = f(b) f(a). R − x 5 The function g(x)= 0 f(t) dt+C is called the anti-derivative of g. The constant C is arbitrary and notR fixed. As we will see below, we can often adjust the constant such that some condition is satisfied. The fundamental theorem of calculus assured us that The anti derivative is the inverse operation of the derivative. Two different anti 0.5 1.0 1.5 2.0 derivatives differ by a constant. 4 The total cost is the antiderivative of the marginal cost of a good. Both the marginal Finding the anti-derivative of a function is much harder than finding the derivative. We will learn cost as well as the total cost are a function of the quantity produced. For instance, suppose some techniques but it is in general not possible to give anti derivatives for even very simple the total cost of making x shoes is 300 and the total cost of making x+4 shoes is 360 for all functions. -

Closed Forms: What They Are and Why We Care
CLOSED FORMS: WHAT THEY ARE AND WHY WE CARE JONATHAN M. BORWEIN AND RICHARD E. CRANDALL Abstract. The term \closed form" is one of those mathematical notions that is commonplace, yet virtually devoid of rigor. And, there is disagreement even on the intuitive side; for example, most everyone would say that π + log 2 is a closed form, but some of us would think that the Euler constant γ is not closed. Like others before us, we shall try to supply some missing rigor to the notion of closed forms and also to give examples from modern research where the question of closure looms both important and elusive. 1. Closed Forms: What They Are Mathematics abounds in terms which are in frequent use yet which are rarely made precise. Two such are rigorous proof and closed form (absent the technical use within differential algebra). If a rigorous proof is \that which `convinces' the appropriate audience" then a closed form is \that which looks `fundamental' to the requisite consumer." In both cases, this is a community-varying and epoch-dependent notion. What was a compelling proof in 1810 may well not be now; what is a fine closed form in 2010 may have been anathema a century ago. In the article we are intentionally informal as befits a topic that intrinsically has no one \right" answer. Let us begin by sampling the Web for various approaches to informal definitions of \closed form." 1.0.1. First approach to a definition of closed form. The first comes from MathWorld [55] and so may well be the first and last definition a student or other seeker-after-easy-truth finds. -

Elementary Functions Received: 03-01-2018 Accepted: 04-02-2018 Sweeti Devi
International Journal of Statistics and Applied Mathematics 2018; 3(2): 07-09 ISSN: 2456-1452 Maths 2018; 3(2): 07-09 © 2018 Stats & Maths Elementary functions www.mathsjournal.com Received: 03-01-2018 Accepted: 04-02-2018 Sweeti Devi Sweeti Devi Assistant Professor, Abstract Bhagat Phool Singh Mahila Elementary function is an introduction to the college mathematics. It aims to provide a working Vishwavidyalaya, Khanpur knowledge of basic functions (exponential, logarithmic and trignometric) fast and efficient Kalan, Haryana, India implementation of elementary function such as sin0, cos0, log0 are of ample importance in a large class of applications. The state of the art method for function evaluation involve either expensive calculations such as multiplication, large number of iteration or large looks up tables. Our proposed method evaluates trignometric, hyperbolic, exponential, logarithmic. Keywords: Power series, logarithmic function, exponential function, trigonometric function Introduction 푥 푥 푥 Elementary functions are 푒 , 푙표푛 , 푎 , sinx, cosx. We all familiar with these functions, but this acquaintances is based on a treatment which was essentially based on intuitive less rigorous geometrical considerations. We shall base the study of these functions on the set of real numbers as a complete ordered field, the nation of limit and convergence of series. As the definitions of function will be based on power series, we start with a brief study of power series. Power Series 2 ℎ 8 ℎ The series of the form 푎표 + 푎 푥 + 푎2 푥 +....... + 푎푛 푥 + …..... = ∑푛=0 푎푛 푥 Are called power series in x and the numbers are their co-efficient. Some simple examples of the power series are. -

Antiderivative and Indefinite Integral
Lecture 25 Antiderivative and Indefinite Integral Objectives ......................................... ...................... 2 Differentiationvsintegration........................... ........................ 3 Antiderivatives ..................................... ....................... 4 Theindefiniteintegral ................................ ....................... 5 Theintegralsign..................................... ...................... 6 Examplesofantiderivatives........................... ......................... 7 Functions and theirderivatives. .. .. .. .. .. .. .. .. .. .. .......................... 8 Functions and their antiderivatives. ........................... 9 Linearity of theanitiderivative. .. .. .. .. .. .. .. .. .. .. ......................... 10 Summary............................................. .................. 11 Comprehension checkpoint ............................. ...................... 12 1 Objectives The rest of our course is devoted to integration. We will discuss indefinite and definite integrals and elementary methods of integration. In this lecture, we define an antiderivative of a function and study its properties. We will define the indefinite integral of a function as its general antiderivative. 2 / 12 Differentiation vs integration Differentiation and integration are the two main operations on functions in calculus. They are opposite in many ways. Differentiation is easy to perform, but difficult to define. Differential calculus appeared relatively recently, about 350 years ago. The definition of derivative