Conclusion – Beyond Sensations Increasingly Divergent Points of View in Acoustics – Analytic and Holistic
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Science of String Instruments
The Science of String Instruments Thomas D. Rossing Editor The Science of String Instruments Editor Thomas D. Rossing Stanford University Center for Computer Research in Music and Acoustics (CCRMA) Stanford, CA 94302-8180, USA [email protected] ISBN 978-1-4419-7109-8 e-ISBN 978-1-4419-7110-4 DOI 10.1007/978-1-4419-7110-4 Springer New York Dordrecht Heidelberg London # Springer Science+Business Media, LLC 2010 All rights reserved. This work may not be translated or copied in whole or in part without the written permission of the publisher (Springer Science+Business Media, LLC, 233 Spring Street, New York, NY 10013, USA), except for brief excerpts in connection with reviews or scholarly analysis. Use in connection with any form of information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed is forbidden. The use in this publication of trade names, trademarks, service marks, and similar terms, even if they are not identified as such, is not to be taken as an expression of opinion as to whether or not they are subject to proprietary rights. Printed on acid-free paper Springer is part of Springer ScienceþBusiness Media (www.springer.com) Contents 1 Introduction............................................................... 1 Thomas D. Rossing 2 Plucked Strings ........................................................... 11 Thomas D. Rossing 3 Guitars and Lutes ........................................................ 19 Thomas D. Rossing and Graham Caldersmith 4 Portuguese Guitar ........................................................ 47 Octavio Inacio 5 Banjo ...................................................................... 59 James Rae 6 Mandolin Family Instruments........................................... 77 David J. Cohen and Thomas D. Rossing 7 Psalteries and Zithers .................................................... 99 Andres Peekna and Thomas D. -

Response Variation of Chladni Patterns on Vibrating Elastic Plate Under Electro-Mechanical Oscillation
Nigerian Journal of Technology (NIJOTECH) Vol. 38, No. 3, July 2019, pp. 540 – 548 Copyright© Faculty of Engineering, University of Nigeria, Nsukka, Print ISSN: 0331-8443, Electronic ISSN: 2467-8821 www.nijotech.com http://dx.doi.org/10.4314/njt.v38i3.1 RESPONSE VARIATION OF CHLADNI PATTERNS ON VIBRATING ELASTIC PLATE UNDER ELECTRO-MECHANICAL OSCILLATION A. E. Ikpe1,*, A. E. Ndon2 and E. M. Etuk3 1, DEPT OF MECHANICAL ENGINEERING, UNIVERSITY OF BENIN, P.M.B. 1154, BENIN, EDO STATE, NIGERIA 2, DEPT OF CIVIL ENGINEERING, AKWA IBOM STATE UNIVERSITY, MKPAT ENIN, AKWA IBOM STATE, NIGERIA 3, DEPT OF PRODUCTION ENGINEERING, UNIVERSITY OF BENIN, P.M.B. 1154, BENIN, EDO STATE, NIGERIA E-mail addresses: 1 [email protected], 2 [email protected], 3 [email protected] ABSTRACT Fine grain particles such as sugar, sand, salt etc. form Chladni patterns on the surface of a thin plate subjected to acoustic excitation. This principle has found its relevance in many scientific and engineering applications where the displacement or response of components under the influence of vibration is vital. This study presents an alternative method of determining the modal shapes on vibrating plate in addition to other existing methods like the experimental method by Ernst Chladni. Three (3) finite element solvers namely: CATIA 2017 version, ANSYS R15.0 2017 version and HYPERMESH 2016 version were employed in the modelling process of the 0.40 mm x 0.40 mm plate and simulation of corresponding mode shapes (Chladni patterns) as well as the modal frequencies using Finite Element Method (FEM). Result of modal frequency obtained from the experimental analysis agreed with the FEM simulated, with HYPERMESH generated results being the closest to the experimental values. -

Standing Waves and Sound
Standing Waves and Sound Waves are vibrations (jiggles) that move through a material Frequency: how often a piece of material in the wave moves back and forth. Waves can be longitudinal (back-and- forth motion) or transverse (up-and- down motion). When a wave is caught in between walls, it will bounce back and forth to create a standing wave, but only if its frequency is just right! Sound is a longitudinal wave that moves through air and other materials. In a sound wave the molecules jiggle back and forth, getting closer together and further apart. Work with a partner! Take turns being the “wall” (hold end steady) and the slinky mover. Making Waves with a Slinky 1. Each of you should hold one end of the slinky. Stand far enough apart that the slinky is stretched. 2. Try making a transverse wave pulse by having one partner move a slinky end up and down while the other holds their end fixed. What happens to the wave pulse when it reaches the fixed end of the slinky? Does it return upside down or the same way up? Try moving the end up and down faster: Does the wave pulse get narrower or wider? Does the wave pulse reach the other partner noticeably faster? 3. Without moving further apart, pull the slinky tighter, so it is more stretched (scrunch up some of the slinky in your hand). Make a transverse wave pulse again. Does the wave pulse reach the end faster or slower if the slinky is more stretched? 4. Try making a longitudinal wave pulse by folding some of the slinky into your hand and then letting go. -
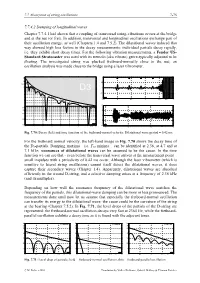
7.7.4.2 Damping of Longitudinal Waves Chapter 7.7.4.1 Had Shown That a Coupling of Transversal String-Vibrations Occurs at the Bridge and at the Nut (Or Fret)
7.7 Absorption of string oscillations 7-75 7.7.4.2 Damping of longitudinal waves Chapter 7.7.4.1 had shown that a coupling of transversal string-vibrations occurs at the bridge and at the nut (or fret). In addition, transversal and longitudinal oscillations exchange part of their oscillation energy, as well (Chapters 1.4 and 7.5.2). The dilatational waves induced that way showed high loss factors in the decay measurements: individual partials decay rapidly, i.e. they exhibit short decay times. For the following vibration measurements, a Fender US- Standard Stratocaster was used with its tremolo (aka vibrato) genre-typically adjusted to be floating. The investigated string was plucked fretboard-normally close to the nut; an oscillation analysis was made close to the bridge using a laser vibrometer. Fig. 7.70: Decay (left) and time function of the fretboard-normal velocity. Dilatational wave period = 0.42 ms. For the fretboard normal velocity, the left-hand image in Fig. 7.70 shows the decay time of the D3-partials. Damping maxima – i.e. T30 minima – can be identified at 2.36, at 4.7 and at 7.1 kHz; resonances of dilatational waves can be assumed to be the cause. In the time function we can see that - even before the transversal wave arrives at the measurement point – small impulses with a periodicity of 0.42 ms occur. Although the laser vibrometer (which is sensitive to lateral string oscillations) cannot itself detect the dilatational waves, it does capture their secondary waves (Chapter 1.4). Apparently, dilatational waves are absorbed efficiently in the wound D-string, and a selective damping arises at a frequency of 2.36 kHz (and its multiples). -

Giant Slinky: Quantitative Exhibit Activity
Name: _________________________________________________________________ Giant Slinky: Quantitative Exhibit Activity Materials: Tape Measure, Stopwatch, & Calculator. In this activity, we will explore wave properties using the Giant Slinky. Let’s start by describing the two types of waves: transverse and longitudinal. Transverse and Longitudinal Waves A transverse wave moves side-to-side orthogonal (at a right angle; perpendicular) to the direction the wave is moving. These waves can be created on the Slinky by shaking the end of it left and right. A longitudinal wave is a pressure wave alternating between high and low pressure. These waves can be created on the Slinky by gathering a few (about 5 or so) Slinky rings, compressing them with your hands and letting go. The area of high pressure is where the Slinky rings are bunched up and the area of low pressure is where the Slinky rings are spread apart. Transverse Waves Before we can do any math with our Slinky, we need to know a little more about its properties. Begin by measuring the length (L) of the Slinky (attachment disk to attachment disk). If your tape measure only measures in feet and inches, convert feet into meters using 1 ft = 0.3048 m. Length of Slinky: L = __________________m We must also know how long it takes a wave to travel the length of the Slinky so that we can calculate the speed of a wave. For now, we are going to investigate transverse waves, so make a single pulse by jerking the Slinky sharply to the left and right ONCE (very quickly) and then return the Slinky to the original center position. -

Orbital Shaped Standing Waves Using Chladni Plates
doi.org/10.26434/chemrxiv.10255838.v1 Orbital Shaped Standing Waves Using Chladni Plates Eric Janusson, Johanne Penafiel, Andrew Macdonald, Shaun MacLean, Irina Paci, J Scott McIndoe Submitted date: 05/11/2019 • Posted date: 13/11/2019 Licence: CC BY-NC-ND 4.0 Citation information: Janusson, Eric; Penafiel, Johanne; Macdonald, Andrew; MacLean, Shaun; Paci, Irina; McIndoe, J Scott (2019): Orbital Shaped Standing Waves Using Chladni Plates. ChemRxiv. Preprint. https://doi.org/10.26434/chemrxiv.10255838.v1 Chemistry students are often introduced to the concept of atomic orbitals with a representation of a one-dimensional standing wave. The classic example is the harmonic frequencies which produce standing waves on a guitar string; a concept which is easily replicated in class with a length of rope. From here, students are typically exposed to a more realistic three-dimensional model, which can often be difficult to visualize. Extrapolation from a two-dimensional model, such as the vibrational modes of a drumhead, can be used to convey the standing wave concept to students more easily. We have opted to use Chladni plates which may be tuned to give a two-dimensional standing wave which serves as a cross-sectional representation of atomic orbitals. The demonstration, intended for first year chemistry students, facilitates the examination of nodal and anti-nodal regions of a Chladni figure which students can then connect to the concept of quantum mechanical parameters and their relationship to atomic orbital shape. File list (4) Chladni manuscript_20191030.docx (3.47 MiB) view on ChemRxiv download file SUPPORTING INFORMATION Materials and Setup Phot.. -

Martinho, Claudia. 2019. Aural Architecture Practice: Creative Approaches for an Ecology of Affect
Martinho, Claudia. 2019. Aural Architecture Practice: Creative Approaches for an Ecology of Affect. Doctoral thesis, Goldsmiths, University of London [Thesis] https://research.gold.ac.uk/id/eprint/26374/ The version presented here may differ from the published, performed or presented work. Please go to the persistent GRO record above for more information. If you believe that any material held in the repository infringes copyright law, please contact the Repository Team at Goldsmiths, University of London via the following email address: [email protected]. The item will be removed from the repository while any claim is being investigated. For more information, please contact the GRO team: [email protected] !1 Aural Architecture Practice Creative Approaches for an Ecology of Affect Cláudia Martinho Goldsmiths, University of London PhD Music (Sonic Arts) 2018 !2 The work presented in this thesis has been carried out by myself, except as otherwise specified. December 15, 2017 !3 Acknowledgments Thanks to: my family, Mazatzin and Sitlali, for their support and understanding; my PhD thesis’ supervisors, Professor John Levack Drever and Dr. Iris Garrelfs, for their valuable input; and everyone who has inspired me and that took part in the co-creation of this thesis practical case studies. This research has been supported by the Foundation for Science and Technology fellowship. Funding has also been granted from the Department of Music and from the Graduate School at Goldsmiths University of London, the arts organisations Guimarães Capital of Culture 2012, Invisible Places and Lisboa Soa, to support the creation of the artworks presented in this research as practical case studies. -

Wave Goodbye to Sound Waves
www.cymascope.com Wave Goodbye to Sound Waves Wave Goodbye to Sound Waves John Stuart Reid Sound is a wave, right? If you share this commonly held belief it is probably because everything you have ever read or been told about sound, whether from high school, popular science books or university courses has said so. And yet, if our eyes could see sound, we would not see waves wiggling their way through the air. Instead, we would see something quite surprising, as you will soon learn. So how did the popular belief in ‘sound waves’ begin? The confusion may have begun with German musician and physicist Ernst Chladni (1756-1827), sometimes described as ‘the father of acoustics.’ Chladni was inspired by the earlier work of English scientist Robert Hooke (1635–1703), who made contributions to many fields including mathematics, optics, mechanics, architecture and astronomy. In 1680 Hooke devised an apparatus consisting of a glass plate covered with flour that he ‘played’ with a violin bow. He was fascinated by the resulting patterns. Around 1800 this phenomenon Ernst Chladni was further explored by Ernst Robert Hooke Chladni, who used a brass plate and sand. Brass is a highly resonant metal and the bell-like sounds he created resulted in the sand grains organizing themselves into complex geometric patterns. These archetypal patterns are now referred to as ‘Chladni Figures,’ although the originator of the invention was actually Hooke. Chladni demonstrated this seemingly magical phenomenon all over Europe and he even had an audience with Napoleon. The French leader was so impressed that he sponsored a competition with The French Academy of Sciences in order to acquire an explanation as to the mechanism behind the sand patterns. -

The Tuning Fork: an Amazing Acoustics Apparatus
FEATURED ARTICLE The Tuning Fork: An Amazing Acoustics Apparatus Daniel A. Russell It seems like such a simple device: a U-shaped piece of metal and Helmholtz resonators were two of the most impor- with a stem to hold it; a simple mechanical object that, when tant items of equipment in an acoustics laboratory. In 1834, struck lightly, produces a single-frequency pure tone. And Johann Scheibler, a silk manufacturer without a scientific yet, this simple appearance is deceptive because a tuning background, created a tonometer, a set of precisely tuned fork exhibits several complicated vibroacoustic phenomena. resonators (in this case tuning forks, although others used A tuning fork vibrates with several symmetrical and asym- Helmholtz resonators) used to determine the frequency of metrical flexural bending modes; it exhibits the nonlinear another sound, essentially a mechanical frequency ana- phenomenon of integer harmonics for large-amplitude lyzer. Scheibler’s tonometer consisted of 56 tuning forks, displacements; and the stem oscillates at the octave of the spanning the octave from A3 220 Hz to A4 440 Hz in steps fundamental frequency of the tines even though the tines of 4 Hz (Helmholtz, 1885, p. 441); he achieved this accu- have no octave component. A tuning fork radiates sound as racy by modifying each fork until it produced exactly 4 a linear quadrupole source, with a distinct transition from beats per second with the preceding fork in the set. At the a complicated near-field to a simpler far-field radiation pat- 1876 Philadelphia Centennial Exposition, Rudolph Koenig, tern. This transition from near field to far field can be seen the premier manufacturer of acoustics apparatus during in the directivity patterns, time-averaged vector intensity, the second half of the nineteenth century, displayed his and the phase relationship between pressure and particle Grand Tonometer with 692 precision tuning forks ranging velocity. -

Apparatus Named After Our Academic Ancestors, III
Digital Kenyon: Research, Scholarship, and Creative Exchange Faculty Publications Physics 2014 Apparatus Named After Our Academic Ancestors, III Tom Greenslade Kenyon College, [email protected] Follow this and additional works at: https://digital.kenyon.edu/physics_publications Part of the Physics Commons Recommended Citation “Apparatus Named After Our Academic Ancestors III”, The Physics Teacher, 52, 360-363 (2014) This Article is brought to you for free and open access by the Physics at Digital Kenyon: Research, Scholarship, and Creative Exchange. It has been accepted for inclusion in Faculty Publications by an authorized administrator of Digital Kenyon: Research, Scholarship, and Creative Exchange. For more information, please contact [email protected]. Apparatus Named After Our Academic Ancestors, III Thomas B. Greenslade Jr. Citation: The Physics Teacher 52, 360 (2014); doi: 10.1119/1.4893092 View online: http://dx.doi.org/10.1119/1.4893092 View Table of Contents: http://scitation.aip.org/content/aapt/journal/tpt/52/6?ver=pdfcov Published by the American Association of Physics Teachers Articles you may be interested in Crystal (Xal) radios for learning physics Phys. Teach. 53, 317 (2015); 10.1119/1.4917450 Apparatus Named After Our Academic Ancestors — II Phys. Teach. 49, 28 (2011); 10.1119/1.3527751 Apparatus Named After Our Academic Ancestors — I Phys. Teach. 48, 604 (2010); 10.1119/1.3517028 Physics Northwest: An Academic Alliance Phys. Teach. 45, 421 (2007); 10.1119/1.2783150 From Our Files Phys. Teach. 41, 123 (2003); 10.1119/1.1542054 This article is copyrighted as indicated in the article. Reuse of AAPT content is subject to the terms at: http://scitation.aip.org/termsconditions. -

Listening to String Sound: a Pedagogical Approach To
LISTENING TO STRING SOUND: A PEDAGOGICAL APPROACH TO EXPLORING THE COMPLEXITIES OF VIOLA TONE PRODUCTION by MARIA KINDT (Under the Direction of Maggie Snyder) ABSTRACT String tone acoustics is a topic that has been largely overlooked in pedagogical settings. This document aims to illuminate the benefits of a general knowledge of practical acoustic science to inform teaching and performance practice. With an emphasis on viola tone production, the document introduces aspects of current physical science and psychoacoustics, combined with established pedagogy to help students and teachers gain a richer and more comprehensive view into aspects of tone production. The document serves as a guide to demonstrate areas where knowledge of the practical science can improve on playing technique and listening skills. The document is divided into three main sections and is framed in a way that is useful for beginning, intermediate, and advanced string students. The first section introduces basic principles of sound, further delving into complex string tone and the mechanism of the violin and viola. The second section focuses on psychoacoustics and how it relates to the interpretation of string sound. The third section covers some of the pedagogical applications of the practical science in performance practice. A sampling of spectral analysis throughout the document demonstrates visually some of the relevant topics. Exercises for informing intonation practices utilizing combination tones are also included. INDEX WORDS: string tone acoustics, psychoacoustics, -

CHLADNI PATTERNS by Tom and Joseph Irvine
CHLADNI PATTERNS By Tom and Joseph Irvine September 18, 2000 Email: [email protected] ______________________________________________________________________ HISTORICAL BACKGROUND Ernst Chladni (1756-1827) was a German physicist who performed experimental studies of vibrating plates. Specifically, he spread fine sand over metal or glass plates. He then excited the fundamental natural frequency of the plate by stroking a violin bow across one of its edges. As a result, a standing wave formed in the plate. A standing wave has "anti-nodes" where the maximum displacement occurs. A standing wave also has "nodes" where no displacement occurs. For a vibrating plate, the nodes occur along "nodal lines." In Chladni's experiment, the sand grains responded to the excitation by migrating to the nodal lines of the plates. The grains thus traced the nodal line pattern. Sophie Germain (1776-1831) derived mathematical equations to describe Chladni's experiments. She published these equations in Memoir on the Vibrations of Elastic Plates. Jules Lissajous (1822-1880) performed further vibration research using Chladni's test methods. THEORY Elastic plates have numerous natural frequencies. The lowest natural frequency is called the fundamental natural frequency. The fundamental frequency is usually the dominant frequency. Each natural frequency has a corresponding "mode." The mode is defined in terms of its nodal line pattern. Each mode has a unique pattern. Points on opposite sides of a nodal line vibrate "180 degrees out-of-phase." Stroking a plate with a violin bow may excite several natural frequencies, thus complicating the experiment. Again, the response will usually be dominated by the fundamental mode. 1 The higher modes can be individually excited, to some extent, by stroking the plate at different edge locations.