Option Spread and Combination Trading
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Machine Learning Based Intraday Calibration of End of Day Implied Volatility Surfaces
DEGREE PROJECT IN MATHEMATICS, SECOND CYCLE, 30 CREDITS STOCKHOLM, SWEDEN 2020 Machine Learning Based Intraday Calibration of End of Day Implied Volatility Surfaces CHRISTOPHER HERRON ANDRÉ ZACHRISSON KTH ROYAL INSTITUTE OF TECHNOLOGY SCHOOL OF ENGINEERING SCIENCES Machine Learning Based Intraday Calibration of End of Day Implied Volatility Surfaces CHRISTOPHER HERRON ANDRÉ ZACHRISSON Degree Projects in Mathematical Statistics (30 ECTS credits) Master's Programme in Applied and Computational Mathematics (120 credits) KTH Royal Institute of Technology year 2020 Supervisor at Nasdaq Technology AB: Sebastian Lindberg Supervisor at KTH: Fredrik Viklund Examiner at KTH: Fredrik Viklund TRITA-SCI-GRU 2020:081 MAT-E 2020:044 Royal Institute of Technology School of Engineering Sciences KTH SCI SE-100 44 Stockholm, Sweden URL: www.kth.se/sci Abstract The implied volatility surface plays an important role for Front office and Risk Manage- ment functions at Nasdaq and other financial institutions which require mark-to-market of derivative books intraday in order to properly value their instruments and measure risk in trading activities. Based on the aforementioned business needs, being able to calibrate an end of day implied volatility surface based on new market information is a sought after trait. In this thesis a statistical learning approach is used to calibrate the implied volatility surface intraday. This is done by using OMXS30-2019 implied volatil- ity surface data in combination with market information from close to at the money options and feeding it into 3 Machine Learning models. The models, including Feed For- ward Neural Network, Recurrent Neural Network and Gaussian Process, were compared based on optimal input and data preprocessing steps. -

Tracking and Trading Volatility 155
ffirs.qxd 9/12/06 2:37 PM Page i The Index Trading Course Workbook www.rasabourse.com ffirs.qxd 9/12/06 2:37 PM Page ii Founded in 1807, John Wiley & Sons is the oldest independent publishing company in the United States. With offices in North America, Europe, Aus- tralia, and Asia, Wiley is globally committed to developing and marketing print and electronic products and services for our customers’ professional and personal knowledge and understanding. The Wiley Trading series features books by traders who have survived the market’s ever changing temperament and have prospered—some by reinventing systems, others by getting back to basics. Whether a novice trader, professional, or somewhere in-between, these books will provide the advice and strategies needed to prosper today and well into the future. For a list of available titles, visit our web site at www.WileyFinance.com. www.rasabourse.com ffirs.qxd 9/12/06 2:37 PM Page iii The Index Trading Course Workbook Step-by-Step Exercises and Tests to Help You Master The Index Trading Course GEORGE A. FONTANILLS TOM GENTILE John Wiley & Sons, Inc. www.rasabourse.com ffirs.qxd 9/12/06 2:37 PM Page iv Copyright © 2006 by George A. Fontanills, Tom Gentile, and Richard Cawood. All rights reserved. Published by John Wiley & Sons, Inc., Hoboken, New Jersey. Published simultaneously in Canada. No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning, or otherwise, except as permitted under Section 107 or 108 of the 1976 United States Copyright Act, without either the prior written permission of the Publisher, or authorization through payment of the appropriate per-copy fee to the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, (978) 750-8400, fax (978) 646-8600, or on the web at www.copyright.com. -

University of Illinois at Urbana-Champaign Department of Mathematics
University of Illinois at Urbana-Champaign Department of Mathematics ASRM 410 Investments and Financial Markets Fall 2018 Chapter 5 Option Greeks and Risk Management by Alfred Chong Learning Objectives: 5.1 Option Greeks: Black-Scholes valuation formula at time t, observed values, model inputs, option characteristics, option Greeks, partial derivatives, sensitivity, change infinitesimally, Delta, Gamma, theta, Vega, rho, Psi, option Greek of portfolio, absolute change, option elasticity, percentage change, option elasticity of portfolio. 5.2 Applications of Option Greeks: risk management via hedging, immunization, adverse market changes, delta-neutrality, delta-hedging, local, re-balance, from- time-to-time, holding profit, delta-hedging, first order, prudent, delta-gamma- hedging, gamma-neutrality, option value approximation, observed values change inevitably, Taylor series expansion, second order approximation, delta-gamma- theta approximation, delta approximation, delta-gamma approximation. Further Exercises: SOA Advanced Derivatives Samples Question 9. 1 5.1 Option Greeks 5.1.1 Consider a continuous-time setting t ≥ 0. Assume that the Black-Scholes framework holds as in 4.2.2{4.2.4. 5.1.2 The time-0 Black-Scholes European call and put option valuation formula in 4.2.9 and 4.2.10 can be generalized to those at time t: −δ(T −t) −r(T −t) C (t; S; δ; r; σ; K; T ) = Se N (d1) − Ke N (d2) P = Ft;T N (d1) − PVt;T (K) N (d2); −r(T −t) −δ(T −t) P (t; S; δ; r; σ; K; T ) = Ke N (−d2) − Se N (−d1) P = PVt;T (K) N (−d2) − Ft;T N (−d1) ; where d1 and d2 are given by S 1 2 ln K + r − δ + 2 σ (T − t) d1 = p ; σ T − t S 1 2 p ln K + r − δ − 2 σ (T − t) d2 = p = d1 − σ T − t: σ T − t 5.1.3 The option value V is a function of observed values, t and S, model inputs, δ, r, and σ, as well as option characteristics, K and T . -

Are Defensive Stocks Expensive? a Closer Look at Value Spreads
Are Defensive Stocks Expensive? A Closer Look at Value Spreads Antti Ilmanen, Ph.D. November 2015 Principal For several years, many investors have been concerned about the apparent rich valuation of Lars N. Nielsen defensive stocks. We analyze the prices of these Principal stocks using value spreads and find that they are not particularly expensive today. Swati Chandra, CFA Vice President Moreover, valuations may have limited efficacy in predicting strategy returns. This piece lends insight into possible reasons by focusing on the contemporaneous relation (i.e., how changes in value spreads are related to returns over the same period). We highlight a puzzling case where a defensive long/short strategy performed well during a recent two- year period when its value spread normalized from abnormally rich levels. For most asset classes, cheapening valuations coincide with poor performance. However, this relationship turns out to be weaker for long/short factor portfolios where several mechanisms can loosen the presumed strong link between value spread changes and strategy returns. Such wedges include changing fundamentals, evolving positions, carry and beta mismatches. Overall, investors should be cognizant of the tenuous link between value spreads and returns. We thank Gregor Andrade, Cliff Asness, Jordan Brooks, Andrea Frazzini, Jacques Friedman, Jeremy Getson, Ronen Israel, Sarah Jiang, David Kabiller, Michael Katz, AQR Capital Management, LLC Hoon Kim, John Liew, Thomas Maloney, Lasse Pedersen, Lukasz Pomorski, Scott Two Greenwich Plaza Richardson, Rodney Sullivan, Ashwin Thapar and David Zhang for helpful discussions Greenwich, CT 06830 and comments. p: +1.203.742.3600 f: +1.203.742.3100 w: aqr.com Are Defensive Stocks Expensive? A Closer Look at Value Spreads 1 Introduction puzzling result — buying a rich investment, seeing it cheapen, and yet making money — in Are defensive stocks expensive? Yes, mildly, more detail below. -

Evidence from SME Bond Markets
Temi di discussione (Working Papers) Asymmetric information in corporate lending: evidence from SME bond markets by Alessandra Iannamorelli, Stefano Nobili, Antonio Scalia and Luana Zaccaria September 2020 September Number 1292 Temi di discussione (Working Papers) Asymmetric information in corporate lending: evidence from SME bond markets by Alessandra Iannamorelli, Stefano Nobili, Antonio Scalia and Luana Zaccaria Number 1292 - September 2020 The papers published in the Temi di discussione series describe preliminary results and are made available to the public to encourage discussion and elicit comments. The views expressed in the articles are those of the authors and do not involve the responsibility of the Bank. Editorial Board: Federico Cingano, Marianna Riggi, Monica Andini, Audinga Baltrunaite, Marco Bottone, Davide Delle Monache, Sara Formai, Francesco Franceschi, Salvatore Lo Bello, Juho Taneli Makinen, Luca Metelli, Mario Pietrunti, Marco Savegnago. Editorial Assistants: Alessandra Giammarco, Roberto Marano. ISSN 1594-7939 (print) ISSN 2281-3950 (online) Printed by the Printing and Publishing Division of the Bank of Italy ASYMMETRIC INFORMATION IN CORPORATE LENDING: EVIDENCE FROM SME BOND MARKETS by Alessandra Iannamorelli†, Stefano Nobili†, Antonio Scalia† and Luana Zaccaria‡ Abstract Using a comprehensive dataset of Italian SMEs, we find that differences between private and public information on creditworthiness affect firms’ decisions to issue debt securities. Surprisingly, our evidence supports positive (rather than adverse) selection. Holding public information constant, firms with better private fundamentals are more likely to access bond markets. Additionally, credit conditions improve for issuers following the bond placement, compared with a matched sample of non-issuers. These results are consistent with a model where banks offer more flexibility than markets during financial distress and firms may use market lending to signal credit quality to outside stakeholders. -

307439 Ferdig Master Thesis
Master's Thesis Using Derivatives And Structured Products To Enhance Investment Performance In A Low-Yielding Environment - COPENHAGEN BUSINESS SCHOOL - MSc Finance And Investments Maria Gjelsvik Berg P˚al-AndreasIversen Supervisor: Søren Plesner Date Of Submission: 28.04.2017 Characters (Ink. Space): 189.349 Pages: 114 ABSTRACT This paper provides an investigation of retail investors' possibility to enhance their investment performance in a low-yielding environment by using derivatives. The current low-yielding financial market makes safe investments in traditional vehicles, such as money market funds and safe bonds, close to zero- or even negative-yielding. Some retail investors are therefore in need of alternative investment vehicles that can enhance their performance. By conducting Monte Carlo simulations and difference in mean testing, we test for enhancement in performance for investors using option strategies, relative to investors investing in the S&P 500 index. This paper contributes to previous papers by emphasizing the downside risk and asymmetry in return distributions to a larger extent. We find several option strategies to outperform the benchmark, implying that performance enhancement is achievable by trading derivatives. The result is however strongly dependent on the investors' ability to choose the right option strategy, both in terms of correctly anticipated market movements and the net premium received or paid to enter the strategy. 1 Contents Chapter 1 - Introduction4 Problem Statement................................6 Methodology...................................7 Limitations....................................7 Literature Review.................................8 Structure..................................... 12 Chapter 2 - Theory 14 Low-Yielding Environment............................ 14 How Are People Affected By A Low-Yield Environment?........ 16 Low-Yield Environment's Impact On The Stock Market........ -

Ice Crude Oil
ICE CRUDE OIL Intercontinental Exchange® (ICE®) became a center for global petroleum risk management and trading with its acquisition of the International Petroleum Exchange® (IPE®) in June 2001, which is today known as ICE Futures Europe®. IPE was established in 1980 in response to the immense volatility that resulted from the oil price shocks of the 1970s. As IPE’s short-term physical markets evolved and the need to hedge emerged, the exchange offered its first contract, Gas Oil futures. In June 1988, the exchange successfully launched the Brent Crude futures contract. Today, ICE’s FSA-regulated energy futures exchange conducts nearly half the world’s trade in crude oil futures. Along with the benchmark Brent crude oil, West Texas Intermediate (WTI) crude oil and gasoil futures contracts, ICE Futures Europe also offers a full range of futures and options contracts on emissions, U.K. natural gas, U.K power and coal. THE BRENT CRUDE MARKET Brent has served as a leading global benchmark for Atlantic Oseberg-Ekofisk family of North Sea crude oils, each of which Basin crude oils in general, and low-sulfur (“sweet”) crude has a separate delivery point. Many of the crude oils traded oils in particular, since the commercialization of the U.K. and as a basis to Brent actually are traded as a basis to Dated Norwegian sectors of the North Sea in the 1970s. These crude Brent, a cargo loading within the next 10-21 days (23 days on oils include most grades produced from Nigeria and Angola, a Friday). In a circular turn, the active cash swap market for as well as U.S. -

Yuichi Katsura
P&TcrvvCJ Efficient ValtmVmm-and Hedging of Structured Credit Products Yuichi Katsura A thesis submitted for the degree of Doctor of Philosophy of the University of London May 2005 Centre for Quantitative Finance Imperial College London nit~ýl. ABSTRACT Structured credit derivatives such as synthetic collateralized debt obligations (CDO) have been the principal growth engine in the fixed income market over the last few years. Val- uation and risk management of structured credit products by meads of Monte Carlo sim- ulations tend to suffer from numerical instability and heavy computational time. After a brief description of single name credit derivatives that underlie structured credit deriva- tives, the factor model is introduced as the portfolio credit derivatives pricing tool. This thesis then describes the rapid pricing and hedging of portfolio credit derivatives using the analytical approximation model and semi-analytical models under several specifications of factor models. When a full correlation structure is assumed or the pricing of exotic structure credit products with non-linear pay-offs is involved, the semi-analytical tractability is lost and we have to resort to the time-consuming Monte Carlo method. As a Monte Carlo variance reduction technique we extend the importance sampling method introduced to credit risk modelling by Joshi [2004] to the general n-factor problem. The large homogeneouspool model is also applied to the method of control variates as a new variance reduction tech- niques for pricing structured credit products. The combination of both methods is examined and it turns out to be the optimal choice. We also show how sensitivities of a CDO tranche can be computed efficiently by semi-analytical and Monte Carlo framework. -

RT Options Scanner Guide
RT Options Scanner Introduction Our RT Options Scanner allows you to search in real-time through all publicly traded US equities and indexes options (more than 170,000 options contracts total) for trading opportunities involving strategies like: - Naked or Covered Write Protective Purchase, etc. - Any complex multi-leg option strategy – to find the “missing leg” - Calendar Spreads Search is performed against our Options Database that is updated in real-time and driven by HyperFeed’s Ticker-Plant and our Implied Volatility Calculation Engine. We offer both 20-minute delayed and real-time modes. Unlike other search engines using real-time quotes data only our system takes advantage of individual contracts Implied Volatilities calculated in real-time using our high-performance Volatility Engine. The Scanner is universal, that is, it is not confined to any special type of option strategy. Rather, it allows determining the option you need in the following terms: – Cost – Moneyness – Expiry – Liquidity – Risk The Scanner offers Basic and Advanced Search Interfaces. Basic interface can be used to find options contracts satisfying, for example, such requirements: “I need expensive Calls for Covered Call Write Strategy. They should expire soon and be slightly out of the money. Do not care much as far as liquidity, but do not like to bear high risk.” This can be done in five seconds - set the search filters to: Cost -> Dear Moneyness -> OTM Expiry -> Short term Liquidity -> Any Risk -> Moderate and press the “Search” button. It is that easy. In fact, if your request is exactly as above, you can just press the “Search” button - these values are the default filtering criteria. -

Users/Robertjfrey/Documents/Work
AMS 511.01 - Foundations Class 11A Robert J. Frey Research Professor Stony Brook University, Applied Mathematics and Statistics [email protected] http://www.ams.sunysb.edu/~frey/ In this lecture we will cover the pricing and use of derivative securities, covering Chapters 10 and 12 in Luenberger’s text. April, 2007 1. The Binomial Option Pricing Model 1.1 – General Single Step Solution The geometric binomial model has many advantages. First, over a reasonable number of steps it represents a surprisingly realistic model of price dynamics. Second, the state price equations at each step can be expressed in a form indpendent of S(t) and those equations are simple enough to solve in closed form. 1+r D-1 u 1 1 + r D 1 + r D y y ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ = u fl u = 1+r D u-1 u 1+r-u 1 u 1 u yd yd ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ1+r D ÅÅÅÅÅÅÅÅ1 uêÅÅÅÅ-ÅÅÅÅu ÅÅ H L H ê L i y As we will see shortlyH weL Hwill solveL the general problemj by solving a zsequence of single step problems on the lattice. That K O K O K O K O j H L H ê L z sequence solutions can be efficientlyê computed because wej only have to zsolve for the state prices once. k { 1.2 – Valuing an Option with One Period to Expiration Let the current value of a stock be S(t) = 105 and let there be a call option with unknown price C(t) on the stock with a strike price of 100 that expires the next three month period. -
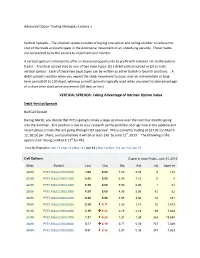
VERTICAL SPREADS: Taking Advantage of Intrinsic Option Value
Advanced Option Trading Strategies: Lecture 1 Vertical Spreads – The simplest spread consists of buying one option and selling another to reduce the cost of the trade and participate in the directional movement of an underlying security. These trades are considered to be the easiest to implement and monitor. A vertical spread is intended to offer an improved opportunity to profit with reduced risk to the options trader. A vertical spread may be one of two basic types: (1) a debit vertical spread or (2) a credit vertical spread. Each of these two basic types can be written as either bullish or bearish positions. A debit spread is written when you expect the stock movement to occur over an intermediate or long- term period [60 to 120 days], whereas a credit spread is typically used when you want to take advantage of a short term stock price movement [60 days or less]. VERTICAL SPREADS: Taking Advantage of Intrinsic Option Value Debit Vertical Spreads Bull Call Spread During March, you decide that PFE is going to make a large up move over the next four months going into the Summer. This position is due to your research on the portfolio of drugs now in the pipeline and recent phase 3 trials that are going through FDA approval. PFE is currently trading at $27.92 [on March 12, 2013] per share, and you believe it will be at least $30 by June 21st, 2013. The following is the option chain listing on March 12th for PFE. View By Expiration: Mar 13 | Apr 13 | May 13 | Jun 13 | Sep 13 | Dec 13 | Jan 14 | Jan 15 Call Options Expire at close Friday, -

A Glossary of Securities and Financial Terms
A Glossary of Securities and Financial Terms (English to Traditional Chinese) 9-times Restriction Rule 九倍限制規則 24-spread rule 24 個價位規則 1 A AAAC see Academic and Accreditation Advisory Committee【SFC】 ABS see asset-backed securities ACCA see Association of Chartered Certified Accountants, The ACG see Asia-Pacific Central Securities Depository Group ACIHK see ACI-The Financial Markets of Hong Kong ADB see Asian Development Bank ADR see American depositary receipt AFTA see ASEAN Free Trade Area AGM see annual general meeting AIB see Audit Investigation Board AIM see Alternative Investment Market【UK】 AIMR see Association for Investment Management and Research AMCHAM see American Chamber of Commerce AMEX see American Stock Exchange AMS see Automatic Order Matching and Execution System AMS/2 see Automatic Order Matching and Execution System / Second Generation AMS/3 see Automatic Order Matching and Execution System / Third Generation ANNA see Association of National Numbering Agencies AOI see All Ordinaries Index AOSEF see Asian and Oceanian Stock Exchanges Federation APEC see Asia Pacific Economic Cooperation API see Application Programming Interface APRC see Asia Pacific Regional Committee of IOSCO ARM see adjustable rate mortgage ASAC see Asian Securities' Analysts Council ASC see Accounting Society of China 2 ASEAN see Association of South-East Asian Nations ASIC see Australian Securities and Investments Commission AST system see automated screen trading system ASX see Australian Stock Exchange ATI see Account Transfer Instruction ABF Hong