Proof Without Words Insight Into a Math Mind: Prof
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Section 124- Unpaid and Unclaimed Dividend
Sr No First Name Middle Name Last Name Address Pincode Folio Amount 1 ASHOK KUMAR GOLCHHA 305 ASHOKA CHAMBERS ADARSHNAGAR HYDERABAD 500063 0000000000B9A0011390 36.00 2 ADAMALI ABDULLABHOY 20, SUKEAS LANE, 3RD FLOOR, KOLKATA 700001 0000000000B9A0050954 150.00 3 AMAR MANOHAR MOTIWALA DR MOTIWALA'S CLINIC, SUNDARAM BUILDING VIKRAM SARABHAI MARG, OPP POLYTECHNIC AHMEDABAD 380015 0000000000B9A0102113 12.00 4 AMRATLAL BHAGWANDAS GANDHI 14 GULABPARK NEAR BASANT CINEMA CHEMBUR 400074 0000000000B9A0102806 30.00 5 ARVIND KUMAR DESAI H NO 2-1-563/2 NALLAKUNTA HYDERABAD 500044 0000000000B9A0106500 30.00 6 BIBISHAB S PATHAN 1005 DENA TOWER OPP ADUJAN PATIYA SURAT 395009 0000000000B9B0007570 144.00 7 BEENA DAVE 703 KRISHNA APT NEXT TO POISAR DEPOT OPP OUR LADY REMEDY SCHOOL S V ROAD, KANDIVILI (W) MUMBAI 400067 0000000000B9B0009430 30.00 8 BABULAL S LADHANI 9 ABDUL REHMAN STREET 3RD FLOOR ROOM NO 62 YUSUF BUILDING MUMBAI 400003 0000000000B9B0100587 30.00 9 BHAGWANDAS Z BAPHNA MAIN ROAD DAHANU DIST THANA W RLY MAHARASHTRA 401601 0000000000B9B0102431 48.00 10 BHARAT MOHANLAL VADALIA MAHADEVIA ROAD MANAVADAR GUJARAT 362630 0000000000B9B0103101 60.00 11 BHARATBHAI R PATEL 45 KRISHNA PARK SOC JASODA NAGAR RD NR GAUR NO KUVO PO GIDC VATVA AHMEDABAD 382445 0000000000B9B0103233 48.00 12 BHARATI PRAKASH HINDUJA 505 A NEEL KANTH 98 MARINE DRIVE P O BOX NO 2397 MUMBAI 400002 0000000000B9B0103411 60.00 13 BHASKAR SUBRAMANY FLAT NO 7 3RD FLOOR 41 SEA LAND CO OP HSG SOCIETY OPP HOTEL PRESIDENT CUFFE PARADE MUMBAI 400005 0000000000B9B0103985 96.00 14 BHASKER CHAMPAKLAL -

Library Catalogue
Id Access No Title Author Category Publisher Year 1 9277 Jawaharlal Nehru. An autobiography J. Nehru Autobiography, Nehru Indraprastha Press 1988 historical, Indian history, reference, Indian 2 587 India from Curzon to Nehru and after Durga Das Rupa & Co. 1977 independence historical, Indian history, reference, Indian 3 605 India from Curzon to Nehru and after Durga Das Rupa & Co. 1977 independence 4 3633 Jawaharlal Nehru. Rebel and Stateman B. R. Nanda Biography, Nehru, Historical Oxford University Press 1995 5 4420 Jawaharlal Nehru. A Communicator and Democratic Leader A. K. Damodaran Biography, Nehru, Historical Radiant Publlishers 1997 Indira Gandhi, 6 711 The Spirit of India. Vol 2 Biography, Nehru, Historical, Gandhi Asia Publishing House 1975 Abhinandan Granth Ministry of Information and 8 454 Builders of Modern India. Gopal Krishna Gokhale T.R. Deogirikar Biography 1964 Broadcasting Ministry of Information and 9 455 Builders of Modern India. Rajendra Prasad Kali Kinkar Data Biography, Prasad 1970 Broadcasting Ministry of Information and 10 456 Builders of Modern India. P.S.Sivaswami Aiyer K. Chandrasekharan Biography, Sivaswami, Aiyer 1969 Broadcasting Ministry of Information and 11 950 Speeches of Presidente V.V. Giri. Vol 2 V.V. Giri poitical, Biography, V.V. Giri, speeches 1977 Broadcasting Ministry of Information and 12 951 Speeches of President Rajendra Prasad Vol. 1 Rajendra Prasad Political, Biography, Rajendra Prasad 1973 Broadcasting Eminent Parliamentarians Monograph Series. 01 - Dr. Ram Manohar 13 2671 Biography, Manohar Lohia Lok Sabha 1990 Lohia Eminent Parliamentarians Monograph Series. 02 - Dr. Lanka 14 2672 Biography, Lanka Sunbdaram Lok Sabha 1990 Sunbdaram Eminent Parliamentarians Monograph Series. 04 - Pandit Nilakantha 15 2674 Biography, Nilakantha Lok Sabha 1990 Das Eminent Parliamentarians Monograph Series. -

Dancing Into the Chthulucene: Sensuous Ecological Activism In
Dancing into the Chthulucene: Sensuous Ecological Activism in the 21st Century Dissertation Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Kelly Perl Klein Graduate Program in Dance Studies The Ohio State University 2019 Dissertation Dr. Harmony Bench, Advisor Dr. Ann Cooper Albright Dr. Hannah Kosstrin Dr. Mytheli Sreenivas Copyrighted by Kelly Perl Klein 2019 2 Abstract This dissertation centers sensuous movement-based performance and practice as particularly powerful modes of activism toward sustainability and multi-species justice in the early decades of the 21st century. Proposing a model of “sensuous ecological activism,” the author elucidates the sensual components of feminist philosopher and biologist Donna Haraway’s (2016) concept of the Chthulucene, articulating how sensuous movement performance and practice interpellate Chthonic subjectivities. The dissertation explores the possibilities and limits of performances of vulnerability, experiences of interconnection, practices of sensitization, and embodied practices of radical inclusion as forms of activism in the context of contemporary neoliberal capitalism and competitive individualism. Two theatrical dance works and two communities of practice from India and the US are considered in relationship to neoliberal shifts in global economic policy that began in the late 1970s. The author analyzes the dance work The Dammed (2013) by the Darpana Academy for Performing Arts in Ahmedabad, -

Vikram Sarabhai (12 August 1919 – 30 December 1971) Was One of the Greatest Scientists of India
Vikram Sarabhai (12 August 1919 – 30 December 1971) was one of the greatest scientists of India. He is considered as the Father of the Indian space program. Apart from being a scientist, he was a rare combination of an innovator, industrialist and visionary. He was instrumental in establishing the Physical Research Laboratory (PRL). He was also the Chairman of the Atomic Energy Commission. He along with other Ahmedabad-based industrialists played a major role in the creation of the Indian Institute of Management, Ahmedabad. He was a great institution builder and established or helped to establish a large number of institutions no less than 42 institutes in diverse fields such as Science, Industry, Management and Education. He also played an instrumental role in the establishment of the Indian Space Research Organization (ISRO). Where & when born Vikram Ambalal Sarabhai was born on August 12, 1919 at Ahmedabad, Gujarat to Ambalal and Sarla Devi. Brief life history of the person Vikram Sarabhai was born as one of eight children in an affluent family of progressive industrialists. He had his early education in a private school, “Retreat” run by his parents on Montessori lines. He grew up in a highly political atmosphere, being part of the elite that led India to independence and subsequently formed its first governments, personally meeting many leaders of the Congress Party such as Jawaharlal Nehru. Vikram’s mother Sarladevi was a social activist, feminist and promoter of Montessori schools in India and his sister was a political activist. His aunt Ansuyaken was a leader of the national labour movement. -

Vikram Sarabhai Loved a Few Cycling Stunts
I NDIAN Mathematics in Madras. He also helped secure a pension for Ramanujan’s wife Janaki who was languishing in poverty. N A TIONAL Such total dedication naturally brought its rewards in results and recognition. Vikram He was elected a Fellow of the Royal S Society of London in 1944, awarded CIENCE Sarabhai the National Science Medal of the United States in 1966, the Padma (1912 - 1971) A Vibhushan from the Government of CADEMY India in 1968 and to crown it all the Nobel Prize for Physics in 1983. INSA As a young boy Vikram Sarabhai loved a few cycling stunts. After his bicycle Sir Isaac Newton’s book Principia, written in 1687, is regarded as the most PLA gained sufficient momentum, he would cross his arms over his chest and place important book in the history of the physical sciences. But it is not easy his feet on the handlebars. If the road ahead was straight he would shut his reading. In 1730, Voltaire described the book as incomprehensible and TINUM JUBILEE eyes and let the bicycle carry him as far as it would go. All this while the terrified obscure. Chandra derived the important results of the Principia by modern servants chased him and begged him to stop. This daredevilry is a bit difficult, techniques. He conceded, however that Newton’s methods were to associate with his later scholarship – author of 80 scholarly papers on aesthetically better. cosmic rays! The seeds of this remarkable life were probably sown in early childhood and Chandra’s books and monographs have all become By: fostered by his unusual upbringing. -

Vikram Sarabhai Library - the Story of Restoration and Upgradation
Volume: 1 | Issue: 3 | February 2019 Tri-annual VIKRAM SARABHAI LIBRARY - THE STORY OF RESTORATION AND UPGRADATION SPECIAL FEATURE FELICITATION ALUMNI WRITE UMEED - 1,000km Prof. AK Jain - Sunsets in Our C1 yclothon| FEBRUARY 2019 50 Years at IIMA Sunset Years alumni.iima.ac.in CONTENTS 2 | FEBRUARY 2019 alumni.iima.ac.in CONTENTS CONTENTS 03 FROM THE EDITOR 05 COVER STORY Vikram Sarabhai Library - The Story of Restoration and Upgradation EDITOR 14 NEWLY JOINED MEMBERS OF IIMA Rakesh Basant BOARD OF GOVERNORS EDITORIAL ASSOCIATE 16 CAMPUS COVERAGE Aarohi Abhishikt Chauhan 28 SPECIAL FEATURE PUBLISHER Fifth edition of UMEED - 1,000km Victor Pereira Cyclothon HEAD- ALUMNI & 35 PROF ABHINANDAN JAIN - EXTERNAL PARTNERSHIPS 50 YEARS AT IIMA Anurag Choudhury 39 MAKING THE IIMA COMMUNITY MANAGER- ALUMNI PROUD RELATIONS S R Mohanty (PGP 1981) - Appointed as Victor Pereira the Chief Secretary of Madhya Pradesh Clerical Assistant Pramod Kunju (PGP 1999) - Lifetime Sreeja Pillai Achievement Award by ABAOC Web Administrator Dr. Pasumarti S. Subbarao (FDP 2008) - Dhyanesh Vyas OdishaInc Award Design & Layout Ms. Chandrika Tandon (PGP 1975) - The Dhruv Parmar Brave Ones Printing 42 WIMWIAN WRITERS Sahitya Mudranalaya Pvt. Ltd 100 Ideas to Improve Governance in India The WIMWIAN is a Balance tri-annual journal of the Indian Institute of Management, Security Analysis Portfolio Management Ahmedabad. Shillong Times Published and printed by Mr. 49 ALUMNI WRITE Victor Pereira, Indian Institute of Management, Vastrapur, Shashi Sharma - Nitty Gritty Ahmedabad - 380015 on behalf of the Indian Institute Self-Management in Times of Climate of Management, Vastrapur, Ahmedabad - 380015, printed Change!!! at Sahitya Mudranalaya Pvt. Ltd., Suresh Bhalla - Sunsets in our Sunset Years City Mill Compound, Kankaria Road, Ahmedabad - 380 022, Tharuvai Srinivasan - In Search of published from Indian Institute of Management, Vastrapur, Happiness Ahmedabad, Gujarat - 380015. -

Padma Vibhushan * * the Padma Vibhushan Is the Second-Highest Civilian Award of the Republic of India , Proceeded by Bharat Ratna and Followed by Padma Bhushan
TRY -- TRUE -- TRUST NUMBER ONE SITE FOR COMPETITIVE EXAM SELF LEARNING AT ANY TIME ANY WHERE * * Padma Vibhushan * * The Padma Vibhushan is the second-highest civilian award of the Republic of India , proceeded by Bharat Ratna and followed by Padma Bhushan . Instituted on 2 January 1954, the award is given for "exceptional and distinguished service", without distinction of race, occupation & position. Year Recipient Field State / Country Satyendra Nath Bose Literature & Education West Bengal Nandalal Bose Arts West Bengal Zakir Husain Public Affairs Andhra Pradesh 1954 Balasaheb Gangadhar Kher Public Affairs Maharashtra V. K. Krishna Menon Public Affairs Kerala Jigme Dorji Wangchuck Public Affairs Bhutan Dhondo Keshav Karve Literature & Education Maharashtra 1955 J. R. D. Tata Trade & Industry Maharashtra Fazal Ali Public Affairs Bihar 1956 Jankibai Bajaj Social Work Madhya Pradesh Chandulal Madhavlal Trivedi Public Affairs Madhya Pradesh Ghanshyam Das Birla Trade & Industry Rajashtan 1957 Sri Prakasa Public Affairs Andhra Pradesh M. C. Setalvad Public Affairs Maharashtra John Mathai Literature & Education Kerala 1959 Gaganvihari Lallubhai Mehta Social Work Maharashtra Radhabinod Pal Public Affairs West Bengal 1960 Naryana Raghvan Pillai Public Affairs Tamil Nadu H. V. R. Iyengar Civil Service Tamil Nadu 1962 Padmaja Naidu Public Affairs Andhra Pradesh Vijaya Lakshmi Pandit Civil Service Uttar Pradesh A. Lakshmanaswami Mudaliar Medicine Tamil Nadu 1963 Hari Vinayak Pataskar Public Affairs Maharashtra Suniti Kumar Chatterji Literature -
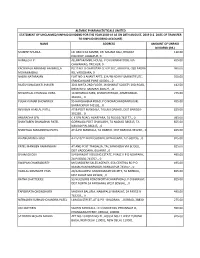
Name Address Amount of Unpaid Dividend (Rs.) Mukesh Shukla Lic Cbo‐3 Ka Samne, Dr
ALEMBIC PHARMACEUTICALS LIMITED STATEMENT OF UNCLAIMED/UNPAID DIVIDEND FOR THE YEAR 2018‐19 AS ON 28TH AUGUST, 2019 (I.E. DATE OF TRANSFER TO UNPAID DIVIDEND ACCOUNT) NAME ADDRESS AMOUNT OF UNPAID DIVIDEND (RS.) MUKESH SHUKLA LIC CBO‐3 KA SAMNE, DR. MAJAM GALI, BHAGAT 110.00 COLONEY, JABALPUR, 0 HAMEED A P . ALUMPARAMBIL HOUSE, P O KURANHIYOOR, VIA 495.00 CHAVAKKAD, TRICHUR, 0 KACHWALA ABBASALI HAJIMULLA PLOT NO. 8 CHAROTAR CO OP SOC, GROUP B, OLD PADRA 990.00 MOHMMADALI RD, VADODARA, 0 NALINI NATARAJAN FLAT NO‐1 ANANT APTS, 124/4B NEAR FILM INSTITUTE, 550.00 ERANDAWANE PUNE 410004, , 0 RAJESH BHAGWATI JHAVERI 30 B AMITA 2ND FLOOR, JAYBHARAT SOCIETY 3RD ROAD, 412.50 KHAR WEST MUMBAI 400521, , 0 SEVANTILAL CHUNILAL VORA 14 NIHARIKA PARK, KHANPUR ROAD, AHMEDABAD‐ 275.00 381001, , 0 PULAK KUMAR BHOWMICK 95 HARISHABHA ROAD, P O NONACHANDANPUKUR, 495.00 BARRACKPUR 743102, , 0 REVABEN HARILAL PATEL AT & POST MANDALA, TALUKA DABHOI, DIST BARODA‐ 825.00 391230, , 0 ANURADHA SEN C K SEN ROAD, AGARPARA, 24 PGS (N) 743177, , 0 495.00 SHANTABEN SHANABHAI PATEL GORWAGA POST CHAKLASHI, TA NADIAD 386315, TA 825.00 NADIAD PIN‐386315, , 0 SHANTILAL MAGANBHAI PATEL AT & PO MANDALA, TA DABHOI, DIST BARODA‐391230, , 0 825.00 B HANUMANTH RAO 4‐2‐510/11 BADI CHOWDI, HYDERABAD, A P‐500195, , 0 825.00 PATEL MANIBEN RAMANBHAI AT AND POST TANDALJA, TAL.SANKHEDA VIA BODELI, 825.00 DIST VADODARA, GUJARAT., 0 SIVAM GHOSH 5/4 BARASAT HOUSING ESTATE, PHASE‐II P O NOAPARA, 495.00 24‐PAGS(N) 743707, , 0 SWAPAN CHAKRABORTY M/S MODERN SALES AGENCY, 65A CENTRAL RD P O 495.00 -

Dr Vikram Sarabhai Memorial Lecture Prof K M Parammasivam
IEICentenaryPublication ACompilationof MemorialLectures presentedin NationalConventionsof AerospaceEngineers 35th IndianEngineeringCongress December18-20,2020 TheInstitutionofEngineers(India) 8GokhaleRoadKolkata700020 Backgroundof DrVikramSarabhaiMemorialLecture Dr Vikram Sarabhai was not only an imaginative and creative scientist but also a pioneering industrialist and astute planner. He made significant contributions in the field of cosmic ray physics and in the development of nuclear power and space programmes. He took up the nuclear programmes with a challenge and added fresh dimensions to the space research programmes in 1966 when he became the Chairman of the Atomic Energy Commission. Dr Sarabhai was born on August 12, 1919 at Ahmedabad in a rich industrialist family. His early education was in a private school and Gujarat College at Ahmedabad. He then went to Cambridge, England and from St John's College obtained his Tripos in 1939. He came back to India and started research work in the field of cosmic rays with Sir C V Raman at the Indian Institute of Science, Bangalore. In 1945, he went back to Cambridge to carry out further research on cosmic rays and there in 1947 obtained Ph D Degree. It was as early as 1942, Dr Sarabhai conceived the idea of starting the Physical Research Laboratory in Ahmedabad. Soon after his return from Cambridge in 1947, Sarabhai started looking for a place for this project. He got a few rooms at the M G Science Institute to start the laboratory and the laboratory was formally opened in April 1954. Dr Sarabhai made the Physical Research Laboratory virtually the cradle of the Indian Space Programme. Dr Sarabhai not only encouraged science but also devoted a good deal of time to industry. -

Contemporary Dance in India Today a Survey
CONTEMPORARY DANCE IN INDIA TODAY A SURVEY Annette Leday With the support of the Centre National de la Danse, Paris (Aide à la recherche et au patrimoine en danse) Translation from the French commissioned by India Foundation for the Arts and Association Keli-Paris 2019 Anita Ratnam (Chennai): "In India the word 'contemporary' applies to anyone who wants to move away from their guru or from the tradition they have learned, to experiment and explore." Mandeep Raikhy (Delhi): "We have rejected the term 'contemporary' and we are still looking for an alternative term." Vikram Iyengar (Kolkata): "I think the various layers of what constitutes "contemporary" in Indian dance have not yet been defined." CONTENTS PREFACE 1 1. INTRODUCTION 4 2. SOME HISTORICAL MARKERS 5 a) Mystifications 5 b) The pioneers of modern dance 7 3. SOME GEOGRAPHIC MARKERS 10 4. A TYPOLOGY OF CONTEMPORARY DANCE IN INDIA 13 a) The 'Neo-Classics' 13 b) Towards radicality 17 c) A suspended space 19 d) Shunning the classics 21 e) Between dance and theatre 22 f) The Bollywood phenomenon 23 g) Commercial contemporaries 25 5. THEMES 26 a) The nurturing techniques 27 b) The issue of Indian identity 28 c) Themes of yesterday and of today 29 d) Dance and politics 30 6. THE CREATIVE PROCESS 33 7. PRESS, CRITIQUE AND FORUMS 35 8. TEACHING AND TRANSMISSION 37 9. VENUES AND FUNDING 41 a) Places of performance 41 b) Festivals 43 c) Working places 45 d) Funding 47 e) Opportunities 48 10. INTERNATIONAL CONTACTS 49 11. PERSPECTIVES 54 12. CONCLUSION 56 PREFACE After a decade immersed in the Kathakali of Kerala, I engaged in a dynamic of contemporary choreography inspired by this great performing tradition. -

Technical Session: Schedule
Decennial Celebration 10 th Karnataka Science and Technology Academy (KSTA) Conference in association with REVA University, Yelahanka, Bengaluru Theme: Science and Technology for Future of Humanity Date: January 18 - 19, 2018 Venue: Kuvempu Auditorium, B’lore Day : Thursday and Friday Inaugural Function: 10.00 am – 11.30 am on January 18, 2018 (Thursday) Technical Session: Schedule DAY 1: January 18, 2018 (Thursday) | Venue: Auditorium Sl. Topic of Presentation Resource Experts Time No Padmabhushan Prof. P. Balaram Is it Necessary for the Society to 12.30 pm - 1 Former Director, IISc Understand Science? Molecular Biophysics Unit 01.15 pm Indian Institute of Science Bengaluru Lunch Break : 1. 15 pm – 2. 15 pm Padmashri Dr. S K Shiva Kumar Space Science & Technology: 02.15 pm - 2 Chairman, KSTA/ Dr. Vikram Sarabhai Future of Humanity Distinguished Professor/ 03.00 pm Former Director, ISAC, ISRO, Bengaluru Prof. Samir K Brahmachari Open Innovation, Big Data and J. C Bose National Fellow 03.00 pm – 3 Crowd Sourcing: The Next Former Director General, Council of Scientific 03.45 pm Frontier and Industrial Research Tea/Coffee Break 3. 45 pm – 4. 15 pm Dr. Y Narahari Professor Data Science Research: Current Game Theory Laboratory Computer Science 04.15 pm – 4 Trends and Future Directions and Automation 05.00 pm Indian Institute of Science Bengaluru Visit to Poster Presentations and Exhibition : 5.00 pm – 6.00 pm Cultural Program : 6.30 pm – 7.30 pm Dinner : 8.00 pm onwards DAY 2: January 19, 2018 (Friday) | Venue: Auditorium Sl. Lecture Topic Resource Expert Time No. Prof. S. Ayyappan Former Secretary to Govt. -

Prof. U.R. Rao Chairman, PRL Council (Former Chairman, ISRO & Secretary, DOS) Department of Space, Antariksh Bhavan New BEL Road, Bangalore – 560 094
INDIA’S SPACE PROGRAM (AN OVERVIEW) (Lecture–1) Prof. U.R. Rao Chairman, PRL Council (Former Chairman, ISRO & Secretary, DOS) Department of Space, Antariksh Bhavan New BEL Road, Bangalore – 560 094 (2006) Slide -1 INDIA DECIDES TO GO INTO SPACE • Background – Ground / Balloon Based Studies, Atmospheric Sciences, Cosmic Rays, Astrophysics • Thumba Equatorial Rocket Launching Station (TERLS) in 1962 Cooperation with NASA, USSR, CNES AND UK Rocket Experiments to Study Equatorial Aeronomy Meteorology and Astrophysics • Population (1.06 Billion), Per capita GDP (550$), Illiteracy (39%), Population Below PL (30%) India with 16% Population, 2% Land, 1.5% Forest, Consumes 2% Energy, has 1.5% Global GDP. India Opts Space Technology for Rapid Socio-Economic Development Slide - 2 INDIAN SPACE ENDEAVOUR There are some who question the relevance of space activities in a developing nation. To us, there is no ambiguity of purpose. We do not have the fantasy of competing with the economically advanced nations in the exploration of the Moon or the planets or manned space-flight. But we are convinced that if we are to play a meaningful role nationally, and in the comity of nations, we must be second to none in the applications of advanced technologies to the real problems of man and society IRS BUDGET Rs 3148 Cr/ annum LAUNCHER APPLICATIONS HUMAN RESOURCES LEADERSHIP EXPERTISE 16500 strong LARGE USER BASE INSAT INTERNATIONAL COOPERATION INDUSTRY VIKRAM A. SARABHAI SPACE ASSETS Remote sensing & SPACE COMMERCE Telecom satellite Constellations INFRASTRUCTURE End-to-end capability STATE OF THE ART TECHNOLOGY Slide - 3 HUMBLE BEGINNING • Establishment of Space Science Tech Center, Thumba-1965 Rocket Technology Development – Centaur – Rohini • Earth Station at Ahmedabad – 1968 / Space Applications Center 1972 Landsat Earth Station – Hyderabad – 1978 • Krishi Darshan (80 Village near Delhi) – Remote Sensing Aerial Expts.