1.3 the Limit of a Function the Aim of This Section Is to Develop the Concept of the Limit of a Function
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Calculus for the Life Sciences I Lecture Notes – Limits, Continuity, and the Derivative
Limits Continuity Derivative Calculus for the Life Sciences I Lecture Notes – Limits, Continuity, and the Derivative Joseph M. Mahaffy, [email protected] Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center San Diego State University San Diego, CA 92182-7720 http://www-rohan.sdsu.edu/∼jmahaffy Spring 2013 Lecture Notes – Limits, Continuity, and the Deriv Joseph M. Mahaffy, [email protected] — (1/24) Limits Continuity Derivative Outline 1 Limits Definition Examples of Limit 2 Continuity Examples of Continuity 3 Derivative Examples of a derivative Lecture Notes – Limits, Continuity, and the Deriv Joseph M. Mahaffy, [email protected] — (2/24) Limits Definition Continuity Examples of Limit Derivative Introduction Limits are central to Calculus Lecture Notes – Limits, Continuity, and the Deriv Joseph M. Mahaffy, [email protected] — (3/24) Limits Definition Continuity Examples of Limit Derivative Introduction Limits are central to Calculus Present definitions of limits, continuity, and derivative Lecture Notes – Limits, Continuity, and the Deriv Joseph M. Mahaffy, [email protected] — (3/24) Limits Definition Continuity Examples of Limit Derivative Introduction Limits are central to Calculus Present definitions of limits, continuity, and derivative Sketch the formal mathematics for these definitions Lecture Notes – Limits, Continuity, and the Deriv Joseph M. Mahaffy, [email protected] — (3/24) Limits Definition Continuity Examples of Limit Derivative Introduction Limits -

Hegel on Calculus
HISTORY OF PHILOSOPHY QUARTERLY Volume 34, Number 4, October 2017 HEGEL ON CALCULUS Ralph M. Kaufmann and Christopher Yeomans t is fair to say that Georg Wilhelm Friedrich Hegel’s philosophy of Imathematics and his interpretation of the calculus in particular have not been popular topics of conversation since the early part of the twenti- eth century. Changes in mathematics in the late nineteenth century, the new set-theoretical approach to understanding its foundations, and the rise of a sympathetic philosophical logic have all conspired to give prior philosophies of mathematics (including Hegel’s) the untimely appear- ance of naïveté. The common view was expressed by Bertrand Russell: The great [mathematicians] of the seventeenth and eighteenth cen- turies were so much impressed by the results of their new methods that they did not trouble to examine their foundations. Although their arguments were fallacious, a special Providence saw to it that their conclusions were more or less true. Hegel fastened upon the obscuri- ties in the foundations of mathematics, turned them into dialectical contradictions, and resolved them by nonsensical syntheses. .The resulting puzzles [of mathematics] were all cleared up during the nine- teenth century, not by heroic philosophical doctrines such as that of Kant or that of Hegel, but by patient attention to detail (1956, 368–69). Recently, however, interest in Hegel’s discussion of calculus has been awakened by an unlikely source: Gilles Deleuze. In particular, work by Simon Duffy and Henry Somers-Hall has demonstrated how close Deleuze and Hegel are in their treatment of the calculus as compared with most other philosophers of mathematics. -

Limits and Derivatives 2
57425_02_ch02_p089-099.qk 11/21/08 10:34 AM Page 89 FPO thomasmayerarchive.com Limits and Derivatives 2 In A Preview of Calculus (page 3) we saw how the idea of a limit underlies the various branches of calculus. Thus it is appropriate to begin our study of calculus by investigating limits and their properties. The special type of limit that is used to find tangents and velocities gives rise to the central idea in differential calcu- lus, the derivative. We see how derivatives can be interpreted as rates of change in various situations and learn how the derivative of a function gives information about the original function. 89 57425_02_ch02_p089-099.qk 11/21/08 10:35 AM Page 90 90 CHAPTER 2 LIMITS AND DERIVATIVES 2.1 The Tangent and Velocity Problems In this section we see how limits arise when we attempt to find the tangent to a curve or the velocity of an object. The Tangent Problem The word tangent is derived from the Latin word tangens, which means “touching.” Thus t a tangent to a curve is a line that touches the curve. In other words, a tangent line should have the same direction as the curve at the point of contact. How can this idea be made precise? For a circle we could simply follow Euclid and say that a tangent is a line that intersects the circle once and only once, as in Figure 1(a). For more complicated curves this defini- tion is inadequate. Figure l(b) shows two lines and tl passing through a point P on a curve (a) C. -

Limits of Functions
Chapter 2 Limits of Functions In this chapter, we define limits of functions and describe some of their properties. 2.1. Limits We begin with the ϵ-δ definition of the limit of a function. Definition 2.1. Let f : A ! R, where A ⊂ R, and suppose that c 2 R is an accumulation point of A. Then lim f(x) = L x!c if for every ϵ > 0 there exists a δ > 0 such that 0 < jx − cj < δ and x 2 A implies that jf(x) − Lj < ϵ. We also denote limits by the `arrow' notation f(x) ! L as x ! c, and often leave it to be implicitly understood that x 2 A is restricted to the domain of f. Note that we exclude x = c, so the function need not be defined at c for the limit as x ! c to exist. Also note that it follows directly from the definition that lim f(x) = L if and only if lim jf(x) − Lj = 0: x!c x!c Example 2.2. Let A = [0; 1) n f9g and define f : A ! R by x − 9 f(x) = p : x − 3 We claim that lim f(x) = 6: x!9 To prove this, let ϵ >p 0 be given. For x 2 A, we have from the difference of two squares that f(x) = x + 3, and p x − 9 1 jf(x) − 6j = x − 3 = p ≤ jx − 9j: x + 3 3 Thus, if δ = 3ϵ, then jx − 9j < δ and x 2 A implies that jf(x) − 6j < ϵ. -

MATH M25BH: Honors: Calculus with Analytic Geometry II 1
MATH M25BH: Honors: Calculus with Analytic Geometry II 1 MATH M25BH: HONORS: CALCULUS WITH ANALYTIC GEOMETRY II Originator brendan_purdy Co-Contributor(s) Name(s) Abramoff, Phillip (pabramoff) Butler, Renee (dbutler) Balas, Kevin (kbalas) Enriquez, Marcos (menriquez) College Moorpark College Attach Support Documentation (as needed) Honors M25BH.pdf MATH M25BH_state approval letter_CCC000621759.pdf Discipline (CB01A) MATH - Mathematics Course Number (CB01B) M25BH Course Title (CB02) Honors: Calculus with Analytic Geometry II Banner/Short Title Honors: Calc/Analy Geometry II Credit Type Credit Start Term Fall 2021 Catalog Course Description Reviews integration. Covers area, volume, arc length, surface area, centers of mass, physics applications, techniques of integration, improper integrals, sequences, series, Taylor’s Theorem, parametric equations, polar coordinates, and conic sections with translations. Honors work challenges students to be more analytical and creative through expanded assignments and enrichment opportunities. Additional Catalog Notes Course Credit Limitations: 1. Credit will not be awarded for both the honors and regular versions of a course. Credit will be awarded only for the first course completed with a grade of "C" or better or "P". Honors Program requires a letter grade. 2. MATH M16B and MATH M25B or MATH M25BH combined: maximum one course for transfer credit. Taxonomy of Programs (TOP) Code (CB03) 1701.00 - Mathematics, General Course Credit Status (CB04) D (Credit - Degree Applicable) Course Transfer Status (CB05) -

Mathematics for Economics Anthony Tay 7. Limits of a Function The
Mathematics for Economics Anthony Tay 7. Limits of a function The concept of a limit of a function is one of the most important in mathematics. Many key concepts are defined in terms of limits (e.g., derivatives and continuity). The primary objective of this section is to help you acquire a firm intuitive understanding of the concept. Roughly speaking, the limit concept is concerned with the behavior of a function f around a certain point (say a ) rather than with the value fa() of the function at that point. The question is: what happens to the value of fx() when x gets closer and closer to a (without ever reaching a )? ln x Example 7.1 Take the function fx()= . 5 x2 −1 4 This function is not defined at the point x =1, because = 3 the denominator at x 1 is zero. However, as x f(x) = ln(x) / (x2-1) 1 2 ‘tends’ to 1, the value of the function ‘tends’ to 2 . We 1 say that “the limit of the function fx() is 2 as x 1 approaches 1, or 0 0 0.5 1 1.5 2 lnx 1 lim = x→1 x2 −1 2 It is important to be clear: the limit of a function and the value of a function are two completely different concepts. In example 7.1, for instance, the value of fx() at x =1 does not even exist; the function is undefined there. However, the limit as x →1 does exist: the value of the function fx() does tend to 1 something (in this case: 2 ) as x gets closer and closer to 1. -
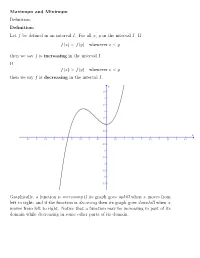
Maximum and Minimum Definition
Maximum and Minimum Definition: Definition: Let f be defined in an interval I. For all x, y in the interval I. If f(x) < f(y) whenever x < y then we say f is increasing in the interval I. If f(x) > f(y) whenever x < y then we say f is decreasing in the interval I. Graphically, a function is increasing if its graph goes uphill when x moves from left to right; and if the function is decresing then its graph goes downhill when x moves from left to right. Notice that a function may be increasing in part of its domain while decreasing in some other parts of its domain. For example, consider f(x) = x2. Notice that the graph of f goes downhill before x = 0 and it goes uphill after x = 0. So f(x) = x2 is decreasing on the interval (−∞; 0) and increasing on the interval (0; 1). Consider f(x) = sin x. π π 3π 5π 7π 9π f is increasing on the intervals (− 2 ; 2 ), ( 2 ; 2 ), ( 2 ; 2 )...etc, while it is de- π 3π 5π 7π 9π 11π creasing on the intervals ( 2 ; 2 ), ( 2 ; 2 ), ( 2 ; 2 )...etc. In general, f = sin x is (2n+1)π (2n+3)π increasing on any interval of the form ( 2 ; 2 ), where n is an odd integer. (2m+1)π (2m+3)π f(x) = sin x is decreasing on any interval of the form ( 2 ; 2 ), where m is an even integer. What about a constant function? Is a constant function an increasing function or decreasing function? Well, it is like asking when you walking on a flat road, as you going uphill or downhill? From our definition, a constant function is neither increasing nor decreasing. -

CHAPTER 2: Limits and Continuity
CHAPTER 2: Limits and Continuity 2.1: An Introduction to Limits 2.2: Properties of Limits 2.3: Limits and Infinity I: Horizontal Asymptotes (HAs) 2.4: Limits and Infinity II: Vertical Asymptotes (VAs) 2.5: The Indeterminate Forms 0/0 and / 2.6: The Squeeze (Sandwich) Theorem 2.7: Precise Definitions of Limits 2.8: Continuity • The conventional approach to calculus is founded on limits. • In this chapter, we will develop the concept of a limit by example. • Properties of limits will be established along the way. • We will use limits to analyze asymptotic behaviors of functions and their graphs. • Limits will be formally defined near the end of the chapter. • Continuity of a function (at a point and on an interval) will be defined using limits. (Section 2.1: An Introduction to Limits) 2.1.1 SECTION 2.1: AN INTRODUCTION TO LIMITS LEARNING OBJECTIVES • Understand the concept of (and notation for) a limit of a rational function at a point in its domain, and understand that “limits are local.” • Evaluate such limits. • Distinguish between one-sided (left-hand and right-hand) limits and two-sided limits and what it means for such limits to exist. • Use numerical / tabular methods to guess at limit values. • Distinguish between limit values and function values at a point. • Understand the use of neighborhoods and punctured neighborhoods in the evaluation of one-sided and two-sided limits. • Evaluate some limits involving piecewise-defined functions. PART A: THE LIMIT OF A FUNCTION AT A POINT Our study of calculus begins with an understanding of the expression lim fx(), x a where a is a real number (in short, a ) and f is a function. -

The Definite Integral
Table of Contents Preface . 1 Chapter 1: Functions and Graphs . 7 1.1 Review of Functions . 8 1.2 Basic Classes of Functions . 36 1.3 Trigonometric Functions . 62 1.4 Inverse Functions . 78 1.5 Exponential and Logarithmic Functions . 96 Chapter 2: Limits . 123 2.1 A Preview of Calculus . 124 2.2 The Limit of a Function . 135 2.3 The Limit Laws . 160 2.4 Continuity . 179 2.5 The Precise Definition of a Limit . 194 Chapter 3: Derivatives . 213 3.1 Defining the Derivative . 214 3.2 The Derivative as a Function . 232 3.3 Differentiation Rules . 247 3.4 Derivatives as Rates of Change . 266 3.5 Derivatives of Trigonometric Functions . 277 3.6 The Chain Rule . 287 3.7 Derivatives of Inverse Functions . 299 3.8 Implicit Differentiation . 309 3.9 Derivatives of Exponential and Logarithmic Functions . 319 Chapter 4: Applications of Derivatives . 341 4.1 Related Rates . 342 4.2 Linear Approximations and Differentials . 354 4.3 Maxima and Minima . 366 4.4 The Mean Value Theorem . 379 4.5 Derivatives and the Shape of a Graph . 390 4.6 Limits at Infinity and Asymptotes . 407 4.7 Applied Optimization Problems . 439 4.8 L’Hôpital’s Rule . 454 4.9 Newton’s Method . 472 4.10 Antiderivatives . 485 Chapter 5: Integration . 507 5.1 Approximating Areas . 508 5.2 The Definite Integral . 529 5.3 The Fundamental Theorem of Calculus . 549 5.4 Integration Formulas and the Net Change Theorem . 566 5.5 Substitution . 584 5.6 Integrals Involving Exponential and Logarithmic Functions . -

3.2 Limits and Continuity of Functions of Two Or More Variables. 3.2.1 Elementary Notions of Limits We Wish to Extend the Notion of Limits Studied in Calculus I
216 CHAPTER 3. FUNCTIONS OF SEVERAL VARIABLES 3.2 Limits and Continuity of Functions of Two or More Variables. 3.2.1 Elementary Notions of Limits We wish to extend the notion of limits studied in Calculus I. Recall that when we write lim f (x) = L, we mean that f can be made as close as we want to x a L, by taking! x close enough to a but not equal to a. In this process, f has to be defined near a, but not necessarily at a. The information we are trying to derive is the behavior of f (x) as x gets closer to a. When we extend this notion to functions of two variables (or more), we will see that there are many similarities. We will discuss these similarities. However, there is also a main difference. The domain of functions of two variables is a subset of R2, in other words it is a set of pairs. A point in R2 is of the form (x, y). So, the equivalent of x a will be (x, y) (a, b). For functions of three variables, the equivalent of!x a will be (x, y,! z) (a, b, c), and so on. This has a very important consequence,! one which makes! computing limits for functions of several variables more diffi cult. While x could only approach a from two directions, from the left or from the right, (x, y) can approach (a, b) from infinitely many directions. In fact, it does not even have to approach (a, b) along a straight path as shown in figure 3.7. -

Calculus Preliminary Exam January 2017
Calculus Preliminary Exam JanuaryJanuary 2017 2016 Duration: 240 minutes Instructions: Answer all questions. The total number of points is 130. 1. (9 pts) Limits: (a) Give an example of a limit of a function that you think is best evaluated by plugging the limit point into this function. Evaluate this limit. (b) Give an example of a limit of a function that you think is best evaluated using L’Hospital’s rule (where algebraic simplifications are not sufficient). Evaluate this limit. (c) Give an example of a limit of a function that you think is best evaluated using L’Hospital’s rule for a different indeterminate form as in (b). Evaluate this limit. 2. (8 pts) Give an example of a use of the fundamental theorem of Calculus to calculate (a) a derivative (b) an integral. 3. (5 pts) Give a word problem such that an equation containing the derivative of a quantity may be obtained from the word description. Clearly indicate the notation you use. 4. (9 pts: 5,4) A line in the xy-plane is given by the equation mx + b y =0. − (a) Derive a formula for the Euclidean distance between a point (x0,y0) and the line (de- note it d(m, b, x0,y0) ). (b) Give an equation describing the curve made of all the points that are located at an equal distance between the line mx + b y =0and the point (x ,y ). − 0 0 For my curiosity (no points), do you know what is the curve obtained above? d(xn) n 1 5. -

Primitive Functions
Lecture 1 (20.2.2019) (translated and slightly adapted from lecture notes by Martin Klazar) (Warning: not a substitute for attending the lectures, probably contains typos. Let me know if you spot any!) Primitive functions Definition 1 (Primitive function). If I ⊆ R is a non-empty open interval and F; f : I ! R are functions satisfying F 0 = f on I, we call F a primitive function of f on I. First, some motivation | the relation of primitive functions with planar figures. For a nonnegative and continuous function f :[a; b] ! R we consider a planar figure 2 U(a; b; f) = f(x; y) 2 R j a ≤ x ≤ b & 0 ≤ y ≤ f(x)g : Its area, whatever it is, is denoted by Z b f := area(U(a; b; f)) : a This is the area of part of the plane defined by the axis x, graph of the function f and the vertical lines y = a and y = b. Two basic relationships between the area and the derivative are as follows. Consider the function F of x defined R x as the area U(a; x; f), i.e., F (x) = a f. The first fundamental theorem of calculus says that for every c 2 [a; b] we have F 0(c) = f(c) | the derivative of a function whose argument x is the upper limit of the U(a; x; f) and the value is its area is equal to the original function f. Thus, R x the function F (x) = a f is a primitive function of f.