Batch Verification of Eddsa Signatures
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

A Public-Key Cryptosystem Based on Discrete Logarithm Problem Over Finite Fields 퐅퐩퐧
IOSR Journal of Mathematics (IOSR-JM) e-ISSN: 2278-5728, p-ISSN: 2319-765X. Volume 11, Issue 1 Ver. III (Jan - Feb. 2015), PP 01-03 www.iosrjournals.org A Public-Key Cryptosystem Based On Discrete Logarithm Problem over Finite Fields 퐅퐩퐧 Saju M I1, Lilly P L2 1Assistant Professor, Department of Mathematics, St. Thomas’ College, Thrissur, India 2Associate professor, Department of Mathematics, St. Joseph’s College, Irinjalakuda, India Abstract: One of the classical problems in mathematics is the Discrete Logarithm Problem (DLP).The difficulty and complexity for solving DLP is used in most of the cryptosystems. In this paper we design a public key system based on the ring of polynomials over the field 퐹푝 is developed. The security of the system is based on the difficulty of finding discrete logarithms over the function field 퐹푝푛 with suitable prime p and sufficiently large n. The presented system has all features of ordinary public key cryptosystem. Keywords: Discrete logarithm problem, Function Field, Polynomials over finite fields, Primitive polynomial, Public key cryptosystem. I. Introduction For the construction of a public key cryptosystem, we need a finite extension field Fpn overFp. In our paper [1] we design a public key cryptosystem based on discrete logarithm problem over the field F2. Here, for increasing the complexity and difficulty for solving DLP, we made a proper additional modification in the system. A cryptosystem for message transmission means a map from units of ordinary text called plaintext message units to units of coded text called cipher text message units. The face of cryptography was radically altered when Diffie and Hellman invented an entirely new type of cryptography, called public key [Diffie and Hellman 1976][2]. -
2.3 Diffie–Hellman Key Exchange
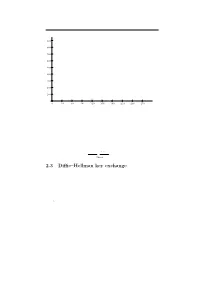
2.3. Di±e{Hellman key exchange 65 q q q q q q 6 q qq q q q q q q 900 q q q q q q q qq q q q q q q q q q q q q q q q q 800 q q q qq q q q q q q q q q qq q q q q q q q q q q q 700 q q q q q q q q q q q q q q q q q q q q q q q q q q qq q 600 q q q q q q q q q q q q qq q q q q q q q q q q q q q q q q q qq q q q q q q q q 500 q qq q q q q q qq q q q q q qqq q q q q q q q q q q q q q qq q q q 400 q q q q q q q q q q q q q q q q q q q q q q q q q 300 q q q q q q q q q q q q q q q q q q qqqq qqq q q q q q q q q q q q 200 q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q q qq q q qq q q 100 q q q q q q q q q q q q q q q q q q q q q q q q q 0 q - 0 30 60 90 120 150 180 210 240 270 Figure 2.2: Powers 627i mod 941 for i = 1; 2; 3;::: any group and use the group law instead of multiplication. -

Post-Quantum Cryptography
Post-quantum cryptography Daniel J. Bernstein & Tanja Lange University of Illinois at Chicago; Ruhr University Bochum & Technische Universiteit Eindhoven 12 September 2020 I Motivation #1: Communication channels are spying on our data. I Motivation #2: Communication channels are modifying our data. I Literal meaning of cryptography: \secret writing". I Achieves various security goals by secretly transforming messages. I Confidentiality: Eve cannot infer information about the content I Integrity: Eve cannot modify the message without this being noticed I Authenticity: Bob is convinced that the message originated from Alice Cryptography with symmetric keys AES-128. AES-192. AES-256. AES-GCM. ChaCha20. HMAC-SHA-256. Poly1305. SHA-2. SHA-3. Salsa20. Cryptography with public keys BN-254. Curve25519. DH. DSA. ECDH. ECDSA. EdDSA. NIST P-256. NIST P-384. NIST P-521. RSA encrypt. RSA sign. secp256k1. Cryptography / Sender Receiver \Alice" \Bob" Tsai Ing-Wen picture credit: By =q府, Attribution, Wikimedia. Donald Trump picture credit: By Shealah Craighead - White House, Public Domain, Wikimedia. Daniel J. Bernstein & Tanja Lange Post-quantum cryptography2 Cryptography with symmetric keys AES-128. AES-192. AES-256. AES-GCM. ChaCha20. HMAC-SHA-256. Poly1305. SHA-2. SHA-3. Salsa20. I Literal meaning of cryptography: \secret writing". Cryptography with public keys Achieves various security goals by secretly transforming messages. BN-254I . Curve25519. DH. DSA. ECDH. ECDSA. EdDSA. NIST P-256. NIST P-384. Confidentiality: Eve cannot infer information about the content NISTI P-521. RSA encrypt. RSA sign. secp256k1. I Integrity: Eve cannot modify the message without this being noticed I Authenticity: Bob is convinced that the message originated from Alice Cryptography / Sender Untrustworthy network Receiver \Alice" \Eve" \Bob" I Motivation #1: Communication channels are spying on our data. -

Making NTRU As Secure As Worst-Case Problems Over Ideal Lattices
Making NTRU as Secure as Worst-Case Problems over Ideal Lattices Damien Stehlé1 and Ron Steinfeld2 1 CNRS, Laboratoire LIP (U. Lyon, CNRS, ENS Lyon, INRIA, UCBL), 46 Allée d’Italie, 69364 Lyon Cedex 07, France. [email protected] – http://perso.ens-lyon.fr/damien.stehle 2 Centre for Advanced Computing - Algorithms and Cryptography, Department of Computing, Macquarie University, NSW 2109, Australia [email protected] – http://web.science.mq.edu.au/~rons Abstract. NTRUEncrypt, proposed in 1996 by Hoffstein, Pipher and Sil- verman, is the fastest known lattice-based encryption scheme. Its mod- erate key-sizes, excellent asymptotic performance and conjectured resis- tance to quantum computers could make it a desirable alternative to fac- torisation and discrete-log based encryption schemes. However, since its introduction, doubts have regularly arisen on its security. In the present work, we show how to modify NTRUEncrypt to make it provably secure in the standard model, under the assumed quantum hardness of standard worst-case lattice problems, restricted to a family of lattices related to some cyclotomic fields. Our main contribution is to show that if the se- cret key polynomials are selected by rejection from discrete Gaussians, then the public key, which is their ratio, is statistically indistinguishable from uniform over its domain. The security then follows from the already proven hardness of the R-LWE problem. Keywords. Lattice-based cryptography, NTRU, provable security. 1 Introduction NTRUEncrypt, devised by Hoffstein, Pipher and Silverman, was first presented at the Crypto’96 rump session [14]. Although its description relies on arithmetic n over the polynomial ring Zq[x]=(x − 1) for n prime and q a small integer, it was quickly observed that breaking it could be expressed as a problem over Euclidean lattices [6]. -

The Discrete Log Problem and Elliptic Curve Cryptography
THE DISCRETE LOG PROBLEM AND ELLIPTIC CURVE CRYPTOGRAPHY NOLAN WINKLER Abstract. In this paper, discrete log-based public-key cryptography is ex- plored. Specifically, we first examine the Discrete Log Problem over a general cyclic group and algorithms that attempt to solve it. This leads us to an in- vestigation of the security of cryptosystems based over certain specific cyclic × groups: Fp, Fp , and the cyclic subgroup generated by a point on an elliptic curve; we ultimately see the highest security comes from using E(Fp) as our group. This necessitates an introduction of elliptic curves, which is provided. Finally, we conclude with cryptographic implementation considerations. Contents 1. Introduction 2 2. Public-Key Systems Over a Cyclic Group G 3 2.1. ElGamal Messaging 3 2.2. Diffie-Hellman Key Exchanges 4 3. Security & Hardness of the Discrete Log Problem 4 4. Algorithms for Solving the Discrete Log Problem 6 4.1. General Cyclic Groups 6 × 4.2. The cyclic group Fp 9 4.3. Subgroup Generated by a Point on an Elliptic Curve 10 5. Elliptic Curves: A Better Group for Cryptography 11 5.1. Basic Theory and Group Law 11 5.2. Finding the Order 12 6. Ensuring Security 15 6.1. Special Cases and Notes 15 7. Further Reading 15 8. Acknowledgments 15 References 16 1 2 NOLAN WINKLER 1. Introduction In this paper, basic knowledge of number theory and abstract algebra is assumed. Additionally, rather than beginning from classical symmetric systems of cryptog- raphy, such as the famous Caesar or Vigni`ere ciphers, we assume a familiarity with these systems and why they have largely become obsolete on their own. -

Secure Authentication Protocol for Internet of Things Achraf Fayad
Secure authentication protocol for Internet of Things Achraf Fayad To cite this version: Achraf Fayad. Secure authentication protocol for Internet of Things. Networking and Internet Archi- tecture [cs.NI]. Institut Polytechnique de Paris, 2020. English. NNT : 2020IPPAT051. tel-03135607 HAL Id: tel-03135607 https://tel.archives-ouvertes.fr/tel-03135607 Submitted on 9 Feb 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Protocole d’authentification securis´ e´ pour les objets connectes´ These` de doctorat de l’Institut Polytechnique de Paris prepar´ ee´ a` Tel´ ecom´ Paris Ecole´ doctorale n◦626 Ecole´ doctorale de l’Institut Polytechnique de Paris (EDIPP) Specialit´ e´ de doctorat : Reseaux,´ informations et communications NNT : 2020IPPAT051 These` present´ ee´ et soutenue a` Palaiseau, le 14 decembre´ 2020, par ACHRAF FAYAD Composition du Jury : Ken CHEN Professeur, Universite´ Paris 13 Nord President´ Pascal LORENZ Professeur, Universite´ de Haute-Alsace (UHA) Rapporteur Ahmed MEHAOUA Professeur, Universite´ Paris Descartes Rapporteur Lyes KHOUKHI Professeur, Ecole´ Nationale Superieure´ d’Ingenieurs´ de Examinateur Caen-ENSICAEN Ahmad FADLALLAH Associate Professor, University of Sciences and Arts in Lebanon Examinateur (USAL) Rida KHATOUN Maˆıtre de conferences,´ Tel´ ecom´ Paris Directeur de these` Ahmed SERHROUCHNI Professeur, Tel´ ecom´ Paris Co-directeur de these` Badis HAMMI Associate Professor, Ecole´ pour l’informatique et les techniques Invite´ avancees´ (EPITA) 626 Acknowledgments First, I would like to thank my thesis supervisor Dr. -

Alternative Elliptic Curve Representations
Alternative Elliptic Curve Representations draft-struik-lwig-curve-representations-00 René Struik Struik Security Consultancy E-mail: [email protected] IETF 101draft-struik – London,-lwig-curve- representationsUK, March-002018 1 Outline 1. The ECC Algorithm Zoo – NIST curve P-256, ECDSA – Curve25519 – Ed25519 2. Implementation Detail 3. How to Reuse Code 4. How to Reuse Existing Standards 5. Conclusions draft-struik-lwig-curve-representations-00 2 ECC Algorithm Zoo (1) NIST curves: Curve model: Weierstrass curve Curve equation: y2 = x3 + ax + b (mod p) Base point: G=(Gx, Gy) Scalar multiplication: addition formulae using, e.g., mixed Jacobian coordinates Point representation: both coordinates of point P=(X, Y) (affine coordinates) 0x04 || X || Y in most-significant-bit/octet first order Examples: NIST P-256 (ANSI X9.62, NIST SP 800-56a, SECG, etc.); Brainpool256r1 (RFC 5639) ECDSA: Signature: R || s in most-significant-bit/octet first order Signing equation: e = s k + d r (mod n), where e=Hash(m) Example: ECDSA, w/ P-256 and SHA-256 (FIPS 186-4, ANSI X9.62, etc.) Note: message m pre-hashed draft-struik-lwig-curve-representations-00 3 ECC Algorithm Zoo (2) CFRG curves: Curve model: Montgomery curve Curve equation: By2 = x3 + Ax2 + x (mod p) Base point: G=(Gx, Gy) Scalar multiplication: Montgomery ladder, using projective coordinates [X: :Z] Point representation: x-coordinate of point P=(X, Y) (x-coordinate-only) X in least-significant-octet, most-significant-bit first order Examples: Curve25519, Curve448 (RFC 7748) DH Key agreement: -

Sieve Algorithms for the Discrete Logarithm in Medium Characteristic Finite Fields Laurent Grémy
Sieve algorithms for the discrete logarithm in medium characteristic finite fields Laurent Grémy To cite this version: Laurent Grémy. Sieve algorithms for the discrete logarithm in medium characteristic finite fields. Cryptography and Security [cs.CR]. Université de Lorraine, 2017. English. NNT : 2017LORR0141. tel-01647623 HAL Id: tel-01647623 https://tel.archives-ouvertes.fr/tel-01647623 Submitted on 24 Nov 2017 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. AVERTISSEMENT Ce document est le fruit d'un long travail approuvé par le jury de soutenance et mis à disposition de l'ensemble de la communauté universitaire élargie. Il est soumis à la propriété intellectuelle de l'auteur. Ceci implique une obligation de citation et de référencement lors de l’utilisation de ce document. D'autre part, toute contrefaçon, plagiat, reproduction illicite encourt une poursuite pénale. Contact : [email protected] LIENS Code de la Propriété Intellectuelle. articles L 122. 4 Code de la Propriété Intellectuelle. articles L 335.2- L 335.10 http://www.cfcopies.com/V2/leg/leg_droi.php -

Security Analysis of the Signal Protocol Student: Bc
ASSIGNMENT OF MASTER’S THESIS Title: Security Analysis of the Signal Protocol Student: Bc. Jan Rubín Supervisor: Ing. Josef Kokeš Study Programme: Informatics Study Branch: Computer Security Department: Department of Computer Systems Validity: Until the end of summer semester 2018/19 Instructions 1) Research the current instant messaging protocols, describe their properties, with a particular focus on security. 2) Describe the Signal protocol in detail, its usage, structure, and functionality. 3) Select parts of the protocol with a potential for security vulnerabilities. 4) Analyze these parts, particularly the adherence of their code to their documentation. 5) Discuss your findings. Formulate recommendations for the users. References Will be provided by the supervisor. prof. Ing. Róbert Lórencz, CSc. doc. RNDr. Ing. Marcel Jiřina, Ph.D. Head of Department Dean Prague January 27, 2018 Czech Technical University in Prague Faculty of Information Technology Department of Computer Systems Master’s thesis Security Analysis of the Signal Protocol Bc. Jan Rub´ın Supervisor: Ing. Josef Kokeˇs 1st May 2018 Acknowledgements First and foremost, I would like to express my sincere gratitude to my thesis supervisor, Ing. Josef Kokeˇs,for his guidance, engagement, extensive know- ledge, and willingness to meet at our countless consultations. I would also like to thank my brother, Tom´aˇsRub´ın,for proofreading my thesis. I cannot express enough gratitude towards my parents, Lenka and Jaroslav Rub´ınovi, who supported me both morally and financially through my whole studies. Last but not least, this thesis would not be possible without Anna who re- lentlessly supported me when I needed it most. Declaration I hereby declare that the presented thesis is my own work and that I have cited all sources of information in accordance with the Guideline for adhering to ethical principles when elaborating an academic final thesis. -

Multi-Party Encrypted Messaging Protocol Design Document, Release 0.3-2-Ge104946
Multi-Party Encrypted Messaging Protocol design document Release 0.3-2-ge104946 Mega Limited, Auckland, New Zealand Guy Kloss <[email protected]> arXiv:1606.04593v1 [cs.CR] 14 Jun 2016 11 January 2016 CONTENTS 1 Strongvelope Multi-Party Encrypted Messaging Protocol 2 1.1 Intent.......................................... ....... 2 1.2 SecurityProperties.............................. ............ 2 1.3 ScopeandLimitations ............................. ........... 3 1.4 Assumptions ..................................... ........ 3 1.5 Messages........................................ ....... 3 1.6 Terminology ..................................... ........ 4 2 Cryptographic Primitives 5 2.1 KeyPairforAuthentication . ............. 5 2.2 KeyAgreement.................................... ........ 5 2.3 (Sender)KeyEncryption. ............ 5 2.4 MessageAuthentication . ............ 6 2.5 MessageEncryption ............................... .......... 6 3 Message Encryption 7 3.1 SenderKeyExchange ............................... ......... 7 3.2 ContentEncryption............................... ........... 8 4 Protocol Encoding 9 4.1 TLVTypes ........................................ ...... 9 4.2 MessageSignatures ............................... .......... 10 4.3 MessageTypes.................................... ........ 10 4.4 KeyedMessages ................................... ........ 10 4.5 FollowupMessages ................................ ......... 10 4.6 AlterParticipantMessages. .............. 11 4.7 LegacySenderKeyEncryption . ............ 11 4.8 SenderKeystoInclude... -

Practical Fault Attack Against the Ed25519 and Eddsa Signature Schemes
Practical fault attack against the Ed25519 and EdDSA signature schemes Yolan Romailler, Sylvain Pelissier Kudelski Security Cheseaux-sur-Lausanne, Switzerland fyolan.romailler,[email protected] main advantages is that its scalar multiplication can be Abstract—The Edwards-curve Digital Signature Algorithm implemented without secret dependent branch and lookup, (EdDSA) was proposed to perform fast public-key digital avoiding the risk of side-channel leakage. More recently, a signatures as a replacement for the Elliptic Curve Digital Signature Algorithm (ECDSA). Its key advantages for em- new digital signature algorithm, namely Ed25519 [6], was bedded devices are higher performance and straightforward, proposed based on the curve edwards25519, i.e., the Edward secure implementations. Indeed, neither branch nor lookup twist of Curve25519. This algorithm was then generalized operations depending on the secret values are performed to other curves and called EdDSA [7]. Due to its various during a signature. These properties thwart many side-channel advantages [7], EdDSA was quickly implemented in many attacks. Nevertheless, we demonstrate here that a single-fault attack against EdDSA can recover enough private key material products and libraries, such as OpenSSH [8]. It was also to forge valid signatures for any message. We demonstrate a recently formally defined in RFC 8032 [9]. practical application of this attack against an implementation The authors of EdDSA did not make any claims about its on Arduino Nano. To the authors’ best knowledge this is the security against fault attacks. However, its resistance to fault first practical fault attack against EdDSA or Ed25519. attacks is discussed in [10]–[12] and taken into account by Keywords-EdDSA; Ed25519; fault attack; digital signature Perrin in [13]. -

(Not) to Design and Implement Post-Quantum Cryptography
SoK: How (not) to Design and Implement Post-Quantum Cryptography James Howe1 , Thomas Prest1 , and Daniel Apon2 1 PQShield, Oxford, UK. {james.howe,thomas.prest}@pqshield.com 2 National Institute of Standards and Technology, USA. [email protected] Abstract Post-quantum cryptography has known a Cambrian explo- sion in the last decade. What started as a very theoretical and mathe- matical area has now evolved into a sprawling research ˝eld, complete with side-channel resistant embedded implementations, large scale de- ployment tests and standardization e˙orts. This study systematizes the current state of knowledge on post-quantum cryptography. Compared to existing studies, we adopt a transversal point of view and center our study around three areas: (i) paradigms, (ii) implementation, (iii) deployment. Our point of view allows to cast almost all classical and post-quantum schemes into just a few paradigms. We highlight trends, common methodologies, and pitfalls to look for and recurrent challenges. 1 Introduction Since Shor's discovery of polynomial-time quantum algorithms for the factoring and discrete logarithm problems, researchers have looked at ways to manage the potential advent of large-scale quantum computers, a prospect which has become much more tangible of late. The proposed solutions are cryptographic schemes based on problems assumed to be resistant to quantum computers, such as those related to lattices or hash functions. Post-quantum cryptography (PQC) is an umbrella term that encompasses the design, implementation, and integration of these schemes. This document is a Systematization of Knowledge (SoK) on this diverse and progressive topic. We have made two editorial choices.