DOCSLIB.ORG

15Th International Ceramics Congress Forum on New Materials

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
15Th International Ceramics Congress Forum on New Materials Abstract Deadline - May 4, 2020 Montecatini Terme - Italy - September 21-29/2020 15th International Ceramics Congress September 21-25/2020 CelebratingYEARS 1970-2020 9th Forum on New Materials September 26-29/2020 www.cimtec-congress.org CIMTEC Invitation to Attend! CIMTEC 2020 - 15th International Conference on Modern Materials and Technologies - will be held in Montecatini Terme, Italy, September 21 to 29, 2020. It will feature the 15th International Ceramics Congress (September 21-25) and the 9th Forum on New Materials (September 26-29), each of them including a number of international Symposia and Conferences. As a major longstanding event for the international materials community in 2020 celebrating its 50th Birthday, CIMTEC will gather together a large and qualified audience of materials scientists, physicists, chemists and of experts of a wide range of the most demanding application engineering areas of modern materials, from the molecular and nanoscales to large complex integrated systems. The Chair, Co-Chairs and CIMTEC 2020 Committees Members invite you to foster the progress in the field by contributing with your expertise to what promises to be a very comprehensive and exciting event, and to enjoy the immense unique artistic heritage and wonderful landscape of Tuscany. Pietro Vincenzini General Chair CIMTEC Conferences National Research Council, Italy Co-Chairs CIMTEC 2020 Mrityunjay Singh Ohio Aerospace Institute, USA World Academy of Ceramics Takashi Goto Tohoku University, Japan International Ceramic Federation Robert P.H. Chang Northwestern University, USA International Union of Materials Research Societies CIMTEC 2020 Montecatini Terme, September 21-29, 2020 15th International Ceramics Congress 9th Forum on New Materials September 21-25, 2020 September 26-29, 2020 Symposium CA - Advances in Processing Science and 2 Symposium FA - 3D Printing and Beyond: State-of-the-art 23 Manufacturing of High Performance Ceramics and Composites and New Paradigms for Additive Manufacturing Technologies Focused Session CA-9 - Bio-inspired and Bio-enabled 3 Processing Symposium FB - Materials Issues in Flexible and 24 Stretchable Electronics for Device Reliability and Performance Focused Session CA-10 - Functionally Graded Materials 3 Focused Session CA-11 - SHS Ceramics 4 Symposium FC - Research Advances on Micro/Nano 25 Systems and their Applications Focused Session CA-12 - Ceramic Joining: From Macro- to 4 Nano-length Scales Symposium FD - Recent Advances in Multiferroic and 25 Special Session CA-13 - Big Data Enhanced Technology for 5 Magnetoelectric Materials and Applications Ceramic Advancements Symposium FE - Functional Nanomaterials for New 26 Symposium CB - Quantification of Microstructures using 6 Generation Solid State Chemical Sensors Data Analysis and Machine Learning Methods Symposium FF - Electromagnetic Metamaterials and 27 Symposium CC - Modelling, Simulation and Testing of 7 Metasurfaces: Recent Research Achievements and New Mechanical and Thermomechanical Properties of Bulk Paradigms Ceramics, Coatings and Composites Symposium FG - Advances in Inorganic Luminescent Symposium CD - High and Ultra High Temperature 7 Materials and Applications 28 Ceramics and Composites for Extreme Environments FH - 4th International Conference 29 Symposium CE - Progress in Nano-laminated Ternary 8 Emerging Materials, Technologies and Applications for Carbides, Nitrides and Borides (MAX/MAB) Phases and Non-volatile Memory Devices Derivatives Thereof (MXenes) Symposium FI - Graphene and Other Emerging 2D-layered 30 Symposium CF - Advances in Functional Materials for Energy 9 Nanomaterials: Synthesis, Properties and Potential Harvesting, Storage and Solar Fuels Applications Symposium CG - Ceramic Thin Films and Coatings for 10 Symposium FJ - Advanced Photocatalytic Materials for 30 Protective, Tribological and Multifunctional Applications Energy and Chemistry in Transition and for Environmental Applications Symposium CH - Porous Ceramics for Environmental 11 Symposium FK - Stimuli Responsive and Multifunctional 32 Protection, Energy-related Technologies and Advanced Polymers: Progress in Materials and Applications Industrial Cycles Symposium FL - State-of-the-art Research and Applications 32 Symposium CI - Progress in Electroceramics Research 12 of Shape Memory Alloys Symposium CJ - Materials Demands Towards Next 13 Symposium FM - Smart and Interactive Textiles - From 33 Generation Electrochemical Energy Storage Systems Nano-engineered Textile Fibres to Integrated Wearable Symposium CK - Solid Oxide Fuel Cells: Materials and 14 Systems Technology Challenges Symposium FN - Embodying Intelligence in Structures and 34 Symposium CL - Inorganic Materials Systems for Advanced 15 Integrated Systems Photonics Symposium FO - Biological, Biohybrid and Bioinspired 36 Symposium CM - Development and Application of Functional 16 Materials: From Electronics and Photonics to Medicine Transparent Conducting and Semiconducting Oxides FP - 13th International Conference 37 Symposium CN - Geopolymers, Inorganic Polymers and 17 Medical Applications of Advanced Biomaterials and Sustainable Materials Nano-biotechnology Symposium CO - Science and Technology for Silicate 18 Focused Session FP-6 - Next Generation Implantable Neural 38 Ceramics Interfaces: New Developments in Materials and Technology Symposium CP - Refractory Materials Challenges to Meet 18 Focused Session FP-7 - Progress in Wireless Body Sensor 38 Current and Future Industry Needs Networks for Healthcare Applications CQ - 9th International Conference 20 Focused Session FP-8 - Progress in 3D Bioprinting of Soft 39 Advanced Inorganic Fibre Composites for Structural and Tissues and Organs Thermal Management Applications th CR - 9 International Conference 21 Information to Authors & Participants 40 Science and Engineering of Novel Superconductors 15th International Ceramics Congress September 21-25, 2020 CA-3 Polymer-derived ceramics Symposium CA (novel preceramic polymers systems, conversion mechanisms, innovative processing for precursor-derived Advances in ceramics, composites, hybrid materials, fibres, coatings, foams; structural and functional characterization, modelling Processing Science of materials, processes and functions) CA-4 Microwave processing and Manufacturing (microwave-material interactions, temperature control during processing, non-contact temperature sensing, microwave assisted synthesis, melting, coating, joining, of High Performance theory and modelling of processes, hybrid processes, scale- Ceramics and up, structural and functional characterization of materials) CA-5 Novel sintering approaches - Spark Plasma, Flash Sintering, Cold Sintering, Laser Sintering Composites (mechanisms and control of SPS, FS and CS, modelling and simulation of electrical field and flash-activated densification, This symposium will highlight recent progress in the hybrid techniques, sintering dynamics, pressure and solvent processing science and manufacturing of advanced effects, phase constitution and crystallization, materials ceramics and composites. Covered are the conventional properties…) powder processing routes, and emerging unconventional or novel techniques capable of embodying ceramic materials with unique properties not possible or difficult to be achieved with traditional methods; approaches that may International Advisory Board also conceive simplified and/or environmentally benign and energy saving “green” processing cycles. Interest Co-Chairs: is for dense and porous bulk materials, (nano)particle Rajendra K. BORDIA, Clemson University, USA reinforced/functionalized composites, thick and thin films, Gary L. MESSING, Penn State University, USA (Convener) laminated and graded structures, hybrid and hierarchical Ralf RIEDEL, Technical University Darmstadt, Germany nanostructures. Rational improvements of the conventional Masahiro YOSHIMURA, National Cheng Kung University, Taiwan methods of powder synthesis, processing and sintering; mechanisms and kinetics involved by novel fabrication Members: techniques; new directions and challenges for the design at Hiroya ABE, Osaka University, Japan Umberto ANSELMI-TAMBURINI, University of Pavia, Italy atomic/molecular scale of complex high performing, micro-, Florence BABONNEAU, Chimie de la Matière Condensée, Paris, meso- and macro-structures with optimized properties for France desired performance; developments in theory, simulations Francis CAMBIER, INS-BCRC, Mons, Belgium and testing will be focus areas of interest for this symposium. Thierry CHARTIER, University of Limoges, France Mari-Ann EINARSRUD, Norwegian University of Science & Session Topics Technology, Norway Begona FERRARI, CSIC, Instituto de Ceramica y Vidrio, Spain CA-1 Advances in conventional powder processing routes Shinobu FUJIHARA, Keio University, Japan - Powder synthesis and characterization(solid state, solution Gregory K.L. GOH, Institute of Matls Research and Eng., A*STAR, Singapore processes, sol-gel, hydrothermal, combustion synthesis, Olivia GRAEVE, University of California, San Diego, USA mechanosynthesis , laser/microwave/plasma assisted Thomas GRAULE, EMPA, Switzerland synthesis…; structure, chemistry, morphology, state of Olivier GUILLON, Forschungszentrum Jülich GmbH, Germany aggregation, packing, flowability, sinterability, …) Masashi HASEGAWA, Nagoya University, Japan - Colloidal processing (surface chemistry, rheology, Shmuel HAYUN, Ben-Gurion University of the Negev, Israel agglomerate softening/removal, new surfactant/ Yoshihiro HIRATA, Kagoshima
Load more

Recommended publications
  • Palmarès 2009 Des Classes Préparatoires Scientifiques
    IV- classes préparatoires BCPST (Biologie, chimie, physique, sciences de la terre) Inscrits Admissibles (1) Admis (1) Intégrés (2) Redoublants (3) Admis en L3 (4) Autres (5) A BIO 67 56 (84%) 39 21 23 3 1 A ENV 54 31 (57%) 15 15 A PC bio 22 15 (68%) 0 Archi Bio 44 35(79,5%) 6 4 G2E 34 19 (54%) 3 1 1) à au moins, un concours 2) total des étudiants inscrits en école à la rentrée 2009 3) dont 12 étudiants admis en Ecole et ayant choisi de redoubler 4) étudiants admis à l’université, en troisième année de licence. 5) étudiants admis à l’université, en deuxième année de licence, ou réorientation (médecine par exemple) ou école intégrée non connue. Intégrés admis PALMARÈS 2009 Banque A Bio, Ecoles des groupes ENSA et ENITA (920 places en 2009) AgroParisTech (Cursus agronome) Paris-Grignon 4 5 AgroParisTech (CA) AgroParisTech (cursus forestier) Nancy (fonctionnaire) 1 1 AgroParisTech (CF) DES CLASSES PRÉPARATOIRES AgroParisTech (cursus forestier) Nancy (civil) 1 AgroParisTech (CF) AgroParisTech (Industries Agricoles et Alimentaires) Massy 3 AgroParisTech (IAA) Etablissement National d’Enseignement Supérieur agronomique de Montpellier 1 Montpelier Sup Agro SCIENTIFIQUES Agrocampus Rennes (cursus agronome) 1 5 Agrocampus Rennes Agrocampus Ouest (cursus horticole et paysage) Angers 1 Agrocampus Angers ENESAD - Agrosup Dijon (Civil) 4 3 ENESAD Dijon ENSBANA - Agrosup Dijon 1 1 ENSBANA Etablissement National d’Enseignement Supérieur agronomique de Toulouse 2 3 ENSAT Toulouse Ecole Nationale Supérieure d’Agronomie et des Industries Alimen- taires de Nancy 2 5 ENSAIA Nancy MP*, MP, PC*, PC, PSI*, BCPST Ecole Nationale d’Ingénieurs des Techniques des Industries Agri- coles et Alimentaires de Nantes 3 1 ENITIAA Nantes Ecole Nationale d’Ingénieurs des Travaux Agricoles 2 2 ENITAB Bordeaux 2 2 ENITAC Clermont-F.
    [Show full text]
  • Mines De Douai
    Les classes préparatoires aux grandes écoles du lycée Jean Bart s’inscrivent dans la philosophie de l’établissement en permettant à de nombreux étudiants du littoral de trouver un enseignement supérieur de qualité sans avoir à s’exiler vers les « grandes » prépas régionales ou parisiennes. Bienveillance et proximité peuvent alors rimer avec exigence et ambition. Le pôle « prépas » se caractérise par son humanisme d’excellence : les années concours, encadrées par des équipes enseignantes impliquées et vigilantes, peuvent être des années de réussite épanouie, bien loin des clichés du prétendu « bagne de la prépa ». Entre 2008 à 2014, on peut souligner tant le grand nombre d’étudiants ayant intégré que la qualité des écoles obtenues : NORMALE SUP (2), CENTRALE (17), MINES (30), CCP (89) dont ENSIMAG (4), E3A et autres (154) dont ARTS ET METIERS (3) et ESTP (10). Palmarès des résultats 2008 Palmarès des résultats 2009 Concours sup : Concours sup : MANIEZ C. (Lycée Angellier, Dunkerque) intègre ENSTIM Douai VANDECRUX B. (Lycée Saint Adrien, Villeneuve d’Ascq) admis à ENSTIM BUXMAN J. (Lycée Mariette, Boulogne) intègre EN Marine Marchande Le Havre Douai POLET A. (Lycée Louis Blaringhem, Béthunes) intègre ISAT Nevers. VANDEWOESTYNE T. (Lycée Angellier, Dunkerque) admis à ENSTIM Douai CAULIER J. (Lycée Angellier) intègre INSA Strasbourg Architecture. Concours ENS-Polythechnique : ROGEZ B. (Lycée Saint Pierre, Calais) intègre ENS Cachan. Concours Centrale-Supélec / Banques associées : DEFURNE M. (Lycée Jean Bart, Dunkerque) intègre CENTRALE Paris Concours Centrale-Supélec / Banques associées : QUIRET S. (Lycée Jean Bart, Dunkerque) admis à CENTRALE Lyon. LEGAY F. (Lycée de l’Europe, Dunkerque) intègre CENTRALE Lille ABOULJAMAL I.
    [Show full text]
  • Undergraduate Handbook
    Undergraduate Handbook Fall 2018 Introduction This handbook provides a summary of information taken from various University of Rochester publications. Also, it includes program-specific details that are of importance to Optics students. This manual contains information regarding changes to the Optics curriculum and should be read carefully and in its entirety. Policies and procedures that apply to the entire university student body take precedence over the policies and procedures contained in this handbook. This handbook is updated to reflect the curriculum changes that are effective as of Fall 2018. Students will follow the curriculum that was in effect at the time when the major or minor was declared. Requirements for Admission to The Institute of Optics Students normally apply for admission to The Institute of Optics during the second semester of their sophomore year. The entrance criteria for the B.S. Degree in Optics and the B.S. degree in Optical Engineering are the same. To be formally admitted tothe major, students will need to satisfy ALL of the following requirements. Students must: 1. Have an overall grade point average (GPA) of at least 2.0 (C) and not be on probation. 2. Have an average GPA of at least 2.0 (C) in PHY 121(P)/122(P)/123 or PHY 141/142/143 (or in comparable courses taken elsewhere). PHY 113 is an acceptable substitute for PHY121. 3. Have an average GPA of at least 2.0 (C) in MTH 161/162/164 or MTH 141/142/143/164 (or in comparable courses taken elsewhere). 4. Have an average GPA of at least 2.0 (C) for all sophomore-level Optics core courses (OPT 241, OPT 201, OPT 261, OPT 202, and OPT 287), with NO grade below a C- for any course and no more than ONE grade of C- in any of these five courses.
    [Show full text]
  • Thesis Finale ENSAIT 24 Aug 2017
    N° d’ordre: 42389 UNIVERSITÉ LILLE 1. SCIENCES ET TECHNOLOGIES École Doctorale Sciences Pour l'Ingénieur Université Lille Nord-de-France ECO-DESIGNED FUNCTIONALIZATION OF POLYESTER FABRIC Doctoral dissertation by Tove AGNHAGE in the partial fulfillment of Erasmus Mundus Joint Doctorate program: Sustainable Management and Design for Textiles Jointly organized by University Lille 1, France, University of Borås, Sweden, and Soochow University, China Presented the 20th of September 2017 at École Nationale Supérieure des Arts et Industries Textiles (ENSAIT) Heikki MATTILA University of Borås Examiner Guido SONNEMANN University of Bordeaux Examiner Isabelle VROMAN University of Reims Examiner Lieva VAN LANGENHOVE Ghent University Examiner Myriam VANNESTE CENTEXBEL, Ghent Examiner Jinping GUAN Soochow University Invited Nemeshwaree BEHARY ENSAIT, Roubaix Invited Anne PERWUELZ ENSAIT, Roubaix Co-director Vincent NIERSTRASZ University of Borås Co-director Guoqiang CHEN Soochow University Co-director Copyright © Tove Agnhage ENSAIT, GEMTEX 2 allée Louise et Victor Champier FR-590 56 Roubaix, France Textile Materials Technology University of Borås SE-501 90 Borås, Sweden College of Textile and Clothing Engineering Soochow University 199 Renai Road CN-215123 Suzhou, China ISBN 978-91-88-269-54-6 (pdf) ABSTRACT There is an increased awareness of the textile dyeing and finishing sector’s high impact on the environment due to high water consumption, polluted wastewater, and inefficient use of energy. To reduce environmental impacts, researchers propose the use of dyes from natural sources. The purpose of using these is to impart new attributes to textiles without compromising on environmental sustainability. The attributes given to the textile can be color and/or other characteristics.
    [Show full text]
  • Mapa De Les Universitats Amb Què Tenim Acord Bilateral Signat, Relacionats Amb Estudis De Grau
    Mapa de les universitats amb què tenim acord bilateral signat, relacionats amb estudis de grau. Aalborg Universitet Aarhus University AGH University of Science and Technology Alytaus kolegija ATEI of Thessaloniki Beijing Institute of Technology BME Brno University of Technology Campus Universitario Dr. Octavio Méndez Pereira Chandigarh University Cologne University of Applied Sciences Cracow University of Technology Cranfield University Çukurova University DCU - Dublin City University E.n.s.m.a. Ecole Centrale de Nantes E.C.N Ecole des mines d'Alès École supérieure d'ingénieurs en électronique et électrotechnique ENSAIT EPF Ecole d'Ingénieurs Escuela Central de Marsella Escuela Superior Politécnica del Litoral (ESPOL) ESEO ESIGELEC Fachhochschule Kärnten Fachhochschule Salzburg Fontys University of Professional Education Gaziantep Universitesi Gdansk University of Technology Gdynia Maritime University Gebze Institute of Technology Ghent University Glyndwr University Hochschule Aalen Hochschule für Angewandte Wissenschaften Hamburg Hochschule Reutlingen Hochschule Rheinmain Hogeschool Utrecht I.U.T. A de Lille I Ingolstadt University of Applied Sciences INSA Lyon Institut National des Sciences Appliquées de Rennes Institut National Polytechnique de Toulouse Institut polytechnique de Grenoble Instituto Tecnológico de Santo Domingo İstanbul Kültür Üniversitesi Istanbul Technical University Istia - School Engineers L'université D'angers ITECH KaHo Sint Lieven - Technologiecampus Gent Kahramanmaras Sutcu Imam University Karel de Grote Hogeschool
    [Show full text]
  • ABIES Journal January 2021
    ABIES Journal January 2021 Table of contents Edito: Tips and tricks from PhD students p.2 The word of a doctoral candidate (Florian) p.2 Challenge “creation d’entreprise” p.4 Next trainings and events (in English) p.5 Prochaines formations (en français) p.6 Job offers p.6 1 TIPS AND TRICKS FROM PHD STUDENTS Notion: a productivity support tool As a PhD student, chances are that you use several applications/tools that help you capture, sort, and organize your ideas (Todoist? Evernote? Word? PDF? ...). The use of these different tools can lead to a disordered accumulation of documents, scattered in multiple places. The information is fragmented and difficult to find. It is in this context that Notion.so can help you. What is it? Simply, it's a PC and mobile application that can change the way you organize yourself by gathering the tools you need in one place. To take notes during meetings, make to-do lists, create spreadsheets, manage your planning and projects (personal and professional) ... All this is possible on Notion.so. Discover this application by visiting: www.notion.so The Pomodoro method Have you ever tried to do several things at once, writing an email while listening to a conversation on the phone for example? If so, have you been fully present, focused, and efficient on these various tasks? It is a safe bet that the answer is no. In order to avoid this scattering, the Pomodoro method can be a good solution. This method of time and goals management proposes to divide one's work into small tasks and to use a timer to perform a specific task during a given time interval, and then to take a short break.
    [Show full text]
  • Schedule of Olympic Fencing Competitions 1896
    Schedule of Olympic Fencing Competitions Event Days Competitors Nations 1896 - Athens Master's Foil 7 April 2 2 Venue: Zappeion Men's Foil Individual 7 April 8 2 Venue: Zappeion Men's Sabre Individual 9 April 5 3 Venue: Zappeion 1900 - Paris Men's Foil Individual 14-19, 21 May 54 9 Venue: La Grande Salle des Fêtes de l'Exposition/Galerie des Machines Master's Foil 22-25, 27-29 May 60 7 Venue: La Grande Salle des Fêtes de l'Exposition/Galerie des Machines Master's Epee 11-14 June 41 4 Venue: La Terrasse du Jeu de Paume aux Tuileries Men's Epee Individual 1-2, 5-7, 9-10, 13-14 June 103 12 Venue: La Terrasse du Jeu de Paume aux Tuileries Master's/Amateur's Epee 15 June 8 2 Venue: La Terrasse du Jeu de Paume aux Tuileries Men's Sabre Individual 19-20, 22,25 June 23 7 Venue: La Grande Salle des Fêtes de l'Exposition/Galerie des Machines Master's Sabre 23, 25-27 June 27 7 Venue: La Grande Salle des Fêtes de l'Exposition/Galerie des Machines 1904 - St. Louis Men's Epee Individual 7 September 5 3 Venue: Physical Culture Gymnasium next to Francis Field Sunday, May 06, 2012 Olympic Fencing Database Page 1 of 17 Schedule of Olympic Fencing Competitions Event Days Competitors Nations Men's Foil Individual 7 September 9 3 Venue: Physical Culture Gymnasium next to Francis Field Men's Foil Team 8 September 6 2 Venue: Physical Culture Gymnasium next to Francis Field Men's Sabre Individual 8 September 5 2 Venue: Physical Culture Gymnasium next to Francis Field Single Sticks 8 September 3 1 Venue: Physical Culture Gymnasium next to Francis Field 1906 -
    [Show full text]
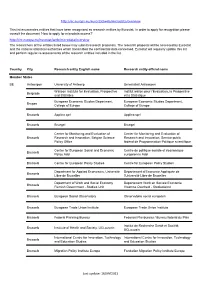
  • Eurostat: Recognized Research Entity
    http://ec.europa.eu/eurostat/web/microdata/overview This list enumerates entities that have been recognised as research entities by Eurostat. In order to apply for recognition please consult the document 'How to apply for microdata access?' http://ec.europa.eu/eurostat/web/microdata/overview The researchers of the entities listed below may submit research proposals. The research proposal will be assessed by Eurostat and the national statistical authorities which transmitted the confidential data concerned. Eurostat will regularly update this list and perform regular re-assessments of the research entities included in the list. Country City Research entity English name Research entity official name Member States BE Antwerpen University of Antwerp Universiteit Antwerpen Walloon Institute for Evaluation, Prospective Institut wallon pour l'Evaluation, la Prospective Belgrade and Statistics et la Statistique European Economic Studies Department, European Economic Studies Department, Bruges College of Europe College of Europe Brussels Applica sprl Applica sprl Brussels Bruegel Bruegel Center for Monitoring and Evaluation of Center for Monitoring and Evaluation of Brussels Research and Innovation, Belgian Science Research and Innovation, Service public Policy Office fédéral de Programmation Politique scientifique Centre for European Social and Economic Centre de politique sociale et économique Brussels Policy Asbl européenne Asbl Brussels Centre for European Policy Studies Centre for European Policy Studies Department for Applied Economics,
    [Show full text]
  • ICN 2020 Committee
    ICN 2020 Committee ICN Steering Committee Pascal Lorenz, University of Haute Alsace, France Yenumula B. Reddy, Grambling State University, USA Eric Renault, Institut Mines-Télécom - Télécom SudParis, France Sherali Zeadally, University of Kentucky, USA ICN Industry/Research Advisory Committee Marc Cheboldaeff, Deloitte Consulting GmbH, Germany Megumi Shibuya, The University of Electro-Communications, Japan Arslan Brömme, Vattenfall GmbH, Berlin, Germany Cristian Anghel, Politehnica University of Bucharest, Romania / Pentalog, France ICN 2020 Technical Program Committee Khelil Abdelmajid, Landshut University of Applied Sciences, Germany Alireza Abdollahpouri, University of Kurdistan, Sanandaj, Iran Abdelmuttlib Ibrahim Abdalla Ahmed, University of Malaya, Malaysia Ahmedin Mohammed Ahmed, FDRE Ministry of Innovation and Technology (MInT), Ethiopia Francisco Airton Silva, Federal University of Piauí, Brazil Sami Marzook Alesawi, King Abdulaziz University | Faculty of Computing and Information Technology at Rabigh, Saudi Arabia Madyan Alsenwi, Kyung Hee University - Global Campus, South Korea Reem Alshahrani, Kent State University, USA Cristian Anghel, Politehnica University of Bucharest, Romania / Pentalog, France Imran Shafique Ansari, University of Glasgow, Scotland, UK Suayb S. Arslan, MEF University, Turkey Mohammed A. Aseeri, King Abdulaziz City of Science and Technology (KACST), Kingdom of Saudi Arabia Michael Atighetchi, BBN Technologies, USA Jocelyn Aubert, Luxembourg Institute of Science and Technology (LIST), Luxembourg Marco Aurélio
    [Show full text]
  • ENSTA Paristech – UPM/ETSIT Presentation of Double- Moving Forward Degree
    ENSTA ParisTech – UPM/ETSIT Presentation of Double- Moving Forward Degree Titre présentation History 1741 Origins Founded by Henry-Louis Duhamel du Monceau, , originally: the School of Henry-Louis Duhamel Construction Engineers of Royal Vessels du Monceau (1700-1782) . General The school became Presentation The National School of Maritime Engineering FIELDS OF EXPERTISE - Mechanical Engineering and Transportation History - Energy Origins of ENSTA - Complex Systems Engineering Merger with 3 other « Grandes Ecoles » 1970 General Ecole Nationale Supérieure de Techniques Avancées Presentation Extension of the spectrum of specialities L'École Nationale L'École Nationale L'École des Ingénieurs Supérieure des Poudres, Supérieure de Hydrographes fondée en 1775. l'Armement, de la Marine, fondée en 1936, fondée en 1814. ENSTA École Nationale Supérieure de Techniques Avancées 32 boulevard Victor, Paris 15ème. Logo in 1970 History ENSTA ParisTech was born 1991 General Founding member of « ParisTech » Presentation ParisTech : 10 « Grandes Ecoles » (Graduate School of Engineering) AgroParis Tech Chimie ParisTech Institut d'Optique Graduate School 2006 École des Ponts ParisTech Mines ParisTech ESPCI ParisTech ENSTA becomes ENSTA ParisTech ENSAE ParisTech Télécom ParisTech ENSTA ParisTech Arts et Métiers ParisTech History ENSTA ParisTech in the Université Paris-Saclay 2012 General Presentation Arrival on Paris-Saclay campus On Ecole polytechnique campus Ici un texte en complément de la page. Un chiffre, une info clé… Partnerships and networks Et encore
    [Show full text]
  • Ultra-Short Multivariate Public Key Signatures – with Public Keys of Degree 2 –
    Ultra-Short Multivariate Public Key Signatures { with Public Keys of Degree 2 { Jacques Patarin1, Gilles Macario-Rat2, Maxime Bros3, and Eliane Koussa1 1 Versailles Laboratory of Mathematics, UVSQ, CNRS, University of Paris-Saclay [email protected], [email protected] 2 Orange, Orange Gardens, 46 avenue de la R´epublique,F-92320 Ch^atillon,France [email protected] 3 University of Limoges, CNRS, XLIM, UMR 7252, F-87000 Limoges, France [email protected] Abstract. In this paper, we study and construct multivariate schemes with \ultra-short" signatures. We focus on the classic case where the public key is a set of multivariate polynomials of degree 2. To design ultra-short signature schemes, we consider that signing a mes- sage and verifying a signature could require up to 1 minute of computa- tion on a modern personal computer. Shorter time could be considered but at the cost of a few additional bits in the signatures, more generally, a trade-off may be found between computation time and signature size, depending on the applications one is targeting. Despite the fact that a time of 1 minute is far bigger than the time re- quired by general purpose multivariate-based signature schemes, such as Rainbow, GeMMS, and Quartz, it enables us to reach ultra-short signa- ture lengths; for instance, around 70 bit-long signatures for a security of 80 bits. In a first part, we describe generic and specific attacks against multivari- ate public key signature schemes and use them to derive the minimal parameters that an ultra-short signature scheme could have.
    [Show full text]
  • Film Film Film Film
    Annette Michelson’s contribution to art and film criticism over the last three decades has been un- paralleled. This volume honors Michelson’s unique C AMERA OBSCURA, CAMERA LUCIDA ALLEN AND TURVEY [EDS.] LUCIDA CAMERA OBSCURA, AMERA legacy with original essays by some of the many film FILM FILM scholars influenced by her work. Some continue her efforts to develop historical and theoretical frame- CULTURE CULTURE works for understanding modernist art, while others IN TRANSITION IN TRANSITION practice her form of interdisciplinary scholarship in relation to avant-garde and modernist film. The intro- duction investigates and evaluates Michelson’s work itself. All in some way pay homage to her extraordi- nary contribution and demonstrate its continued cen- trality to the field of art and film criticism. Richard Allen is Associ- ate Professor of Cinema Studies at New York Uni- versity. Malcolm Turvey teaches Film History at Sarah Lawrence College. They recently collaborated in editing Wittgenstein, Theory and the Arts (Lon- don: Routledge, 2001). CAMERA OBSCURA CAMERA LUCIDA ISBN 90-5356-494-2 Essays in Honor of Annette Michelson EDITED BY RICHARD ALLEN 9 789053 564943 MALCOLM TURVEY Amsterdam University Press Amsterdam University Press WWW.AUP.NL Camera Obscura, Camera Lucida Camera Obscura, Camera Lucida: Essays in Honor of Annette Michelson Edited by Richard Allen and Malcolm Turvey Amsterdam University Press Front cover illustration: 2001: A Space Odyssey. Courtesy of Photofest Cover design: Kok Korpershoek, Amsterdam Lay-out: japes, Amsterdam isbn 90 5356 494 2 (paperback) nur 652 © Amsterdam University Press, Amsterdam, 2003 All rights reserved. Without limiting the rights under copyright reserved above, no part of this book may be reproduced, stored in or introduced into a retrieval system, or transmitted, in any form or by any means (electronic, me- chanical, photocopying, recording or otherwise) without the written permis- sion of both the copyright owner and the author of the book.
    [Show full text]