DOCSLIB.ORG

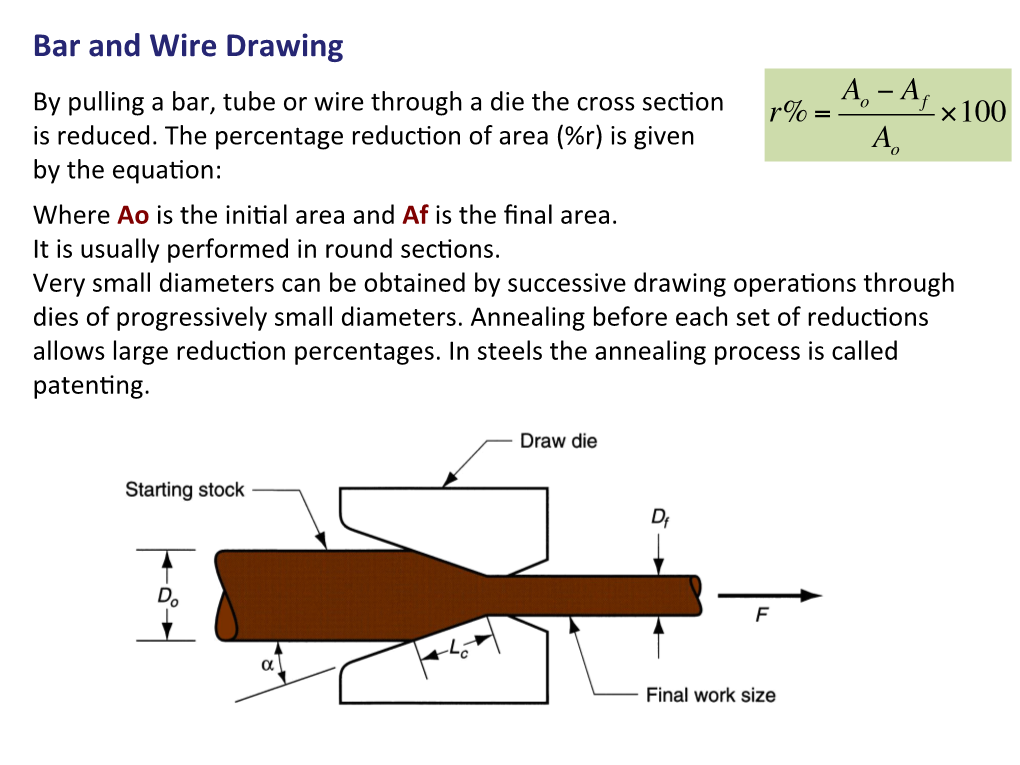
Wire Drawing a − a by Pulling a Bar, Tube Or Wire Through a Die the Cross SecOn R% = O F ×100 Is Reduced

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Wire Drawing a − a by Pulling a Bar, Tube Or Wire Through a Die the Cross Sec�On R% = O F ×100 Is Reduced Bar and Wire Drawing A − A By pulling a bar, tube or wire through a die the cross sec6on r% = o f ×100 is reduced. The percentage reduc6on of area (%r) is given Ao by the equaon: Where Ao is the ini6al area and Af is the final area. It is usually performed in round sec6ons. Very small diameters can be obtained by successive drawing operaons through dies of progressively small diameters. Annealing before each set of reduc6ons allows large reduc6on percentages. In steels the annealing process is called paten6ng. When drawing hard materials, the working face of the die is made of tungsten carbide (WC) by powder metallurgy. For very fine diameters a diamond impregnated die is preferred. In a mul6ple die configuraon, the pulling force through the die is provided by each of the drums (capstan drums). Mechanics of Wire Drawing and Extrusion Direct extrusion with the diametral area reduced from Ao to Af. Then the ideal work is given by: " % ε f A " 1 % w = σ δε σ = Kε n ε = ε = ln$ o ' = ln = ε ideal ∫ 0 f axial $ ' $ ' homogeneous # Af & #1− r & n+1 ε f n Kε w = Kε δε = h if n = 0 ⇒ w = Yε i ∫ 0 n +1 h FΔl Where Wi is the external work, Pe is the applied Wi = FΔl ⇒ wi = = Pe extrusion pressure and σd is the applied drawing AoΔl stress . In reality: Kε n+1 P = σ ≥ h e d n +1 Taking into consideraon fric6on (work due to inhomogeneous deformaon, then wtotal = wideal + w friction Slab Analysis for Wire Drawing and Extrusion Equilibrium Expanding and eliminang higher orders π 2 π 2 π Dδx π Dδx (σ x +δσ x ) (D +δD) −σ x D + p sinα + µp cosα = 0 4 4 cosα cosα π 2 2 π 2 (σ x +δσ x ) D + 2DδD +δD −σ x D + pπ Dδx tanα + µpπ Dδx = 0 4 ( ) 4 π 2 2σ DδD + D δσ + pπ Dδx tanα + µpπ Dδx = 0 4 ( x x ) 2σ xδD + Dδσ x + 4pδx tanα + 4µpδx = 0 D δ δD tanα = 2 ⇒ δx = δx 2tanα δD 2σ δD + Dδσ + 2pδD + 2µp = 0 x x tanα # µ & 2σ xδD + Dδσ x + 2p%1+ (δD = 0 $ tanα ' Using Maximum Shear Stress (Tresca Criterium) σ + p = σ = 2τ δD δ p x flow flow = ' ! $* δσ x = −δ p D 2µ )4τ flow + p# &, " µ % ( " tanα %+ 4τ flowδD − 2pδD + 2p$1+ 'δD = Dδ p # tanα & δD δσ = x ( + D ! 2µ $ ! 2µ $ δD " 2µ % σ − 2τ 2 + *4τ flow + p$ '- = δ p x # & flow # & D ) # tanα &, " tanα % " tanα % Do δD σ xo δσ = x ∫ D ∫ f D σ xf " 2µ % " 2µ % σ $ '− 2τ $2 + ' x # tanα & flow # tanα & " µ % " µ % " µ % 1+ ) 2$ ', 2$ ' $ ' " % # tanα & " % # tanα & σ xf # tanα &+ Df . σ xo Df = +1−$ ' .+ $ ' 2τ flow " µ % # Do & 2τ flow # Do & $ ' *+ -. # tanα & σxo is the back stress (tension) In wire drawing, the usual condi6ons are σxf is the pulling stress (tension) σxo=0 and 2τflow=Y so the equaon becomes: ! µ $ ( # &+ " tanα % ! tanα $ ! Af $ Y 1 *1 - σ xf = σ drawing = # + &* −# & - " µ % " Ao % )* ,- In extrusion, the usual condi6ons are σxf=0 , σxo is negave and 2τflow=Y so the equaon becomes: " µ % ( $ ' + " % " %# tanα & tanα * Ao - (−σ xo ) = pextrusion = Y $1+ '*$ ' −1- # µ & # Af & )* ,- Maximum ReducCon of Area – Wire Drawing n For failure drawn stress = material flow (yield) stress. σ drawing = Kε Typical values of α=6degrees and µ=0.1 Kε n Material with a strain hardening constant K=760MPa and 2τ = σ = Y = strain hardening exponent n=0.19 flow flow n +1 ! µ $ ( # &+ " tanα % n σ drawing ! tanα $* ! Af $ - Kε = 1+ 1− = # &* # & - n Y " µ % " Ao % Kε )* ,- n +1 ! 0.1 $ ( # &+ " tan6 % ! tan6 $* ! Af $ - Ao − Af 0.19 +1= #1+ &*1−# & - ⇒ = RA = 0.58 " 0.1 % " Ao % Ao )* ,- The maximum reduc6on of area must be solved for each µ, α and back tension Taking into consideraon fric6on and redundant work (work due to inhomogeneous deformaon, then wtotal = wideal + w friction + wredundant ! µ $ . ( # &+ 2 " tanα % 0! tanα $ ! Af $ 4 2 !1− r $0 Y 1 *1 - σ drawing = /# + &* −# & -+ α # &3 0" µ % " Ao % 3 3 " r %0 1 )* ,- 4 ! µ $ ! A $ Y 1 ln# o & σ d = Φ # + & # & AXer simplificaons " α % " Af % ! D $ Φ =1+ 0.12# average & L n " contact % Kε 2τ flow = σ flow = Y = Strain Hardening – Cold below RecrystallizaCon temperature n +1 Take the average flow stress (Tresca) – due to shape effect m 2τ flow = σ flow = Y = Cε Strain Rate Effect – Hot above Recrystallizaon Temperature For a round part (the average strain rate ε, vo is the velocity at 6v D2 ⋅ tanα # A & o o ln% o ( the ini6al area and A is the area ε = 3 3 % ( Do − Df $ Af ' 6V For poor lubricaon the expression of the true strain rate is ε = 0 ln R D0 Considering only the ideal work and the expression for Energy per Unit Volume n+1 n ! $ Kεh Kεh Ao Pe = σ d = = εh = Yεh = Y ln# & n +1 n +1 " Af % Considering only the ideal work, then, the expression for the force required for drawing and the expression for the Fd = σ d Af power required are: Pd = Fdv f = σ d Af v f ! $ Drawing Limit (Ideal): Ao Pe = σ d = Y ln# & Max − Stress = Y " Af % For a Perfectly PlasCc Material. The ideal maximum reduc6on per pass is ! $ ! $ Ao Ao 63% σ d = Y = Y ln# & ⇒ ln# & =1 " Af % " Af % ! $ Ao Ao − Af # & = e ⇒ = 0.63 " Af % Ao For a Strain Hardening Material. The ! $ n+1 ideal maximum reduc6on per pass Ao Kεh σ d = Y ln# & = depends on the strain hardening " Af % n +1 coefficient. Example for n=0.19 then n+1 n n Kε the maximum reduc6on per pass is Max.Stress = Kε ⇒ Kε = h 69.5% n +1 A − A ε = n +1 ⇒ o f =1− e−(n+1) Ao Example A round rod of annealed 302 stainless steel is being drawn from a diameter of 10mm to 8mm at a speed of 0.5m/s. Assume that the fric6onal and redundant work together cons6tute 40% of the ideal work of deformaon. (a) Calculate the power required in this operaon, and (b) the die pressure at the exit of the die. Data: strain hardening exponent = 0.3 ; strain hardening coefficient = 1300MPa !10 $2 ε1 = ln# & = 0.446 Calculate the true strain " 8 % Kε n Calculate the average flow stress Y = = 785 MPa n +1 !10 $2 Calculate the drawing stress σ d = Y ln# & = 785MPa × 0.446 = 350MPa " 8 % "π 2 % "π 2 % Fd = σ d ×$ Df ' = 350MPa ×$ 0.008 ' =17598N Calculate the drawing force # 4 & # 4 & Calculate the power P = Fd × v =17598N × 0.5m / s = 8799W The actual power will be 40% higher, i.e. 12.319kW P 12319W Calculate the actual force F = = = 24637N d v 0.5m / s Fd Calculate the actual stress σ d = = 490MPa Af n 0.30 Calculate the flow stress of the material Yf = Kε1 = (1300)(0.446) =1020MPa Calculate the die pressure p = Yf −σ d =1020 − 490 = 530MPa Example Wire of ini6al diameter = 0.125 in. is drawn through two dies each providing a 0.20 area reduc6on. The metal has a strength coefficient = 40,000 lb/in.2 and a strain hardening exponent =0.15. The dies have an entrance angle of 12o, and the es6mated coefficient of fric6on is 0.10. The motors driving the capstans can each deliver 1.50 HP at 90% efficiency. Determine the maximum possible speed of the wire as it exits the second die. 2 2 DO − Df Diameters aer the first and second r = 2 = 0.2 ⇒ Df 1 = 0.112 ⇒ Df 2 = 0.1 pass DO ! $ DO ! 0.125 $ ! 0.1118$ ε = 2ln# & = 2ln# & = 2ln# & = 0.2232 " Df % " 0.1118% " 0.10 % ! 1 $ n 40000 0.15 First Die Y = # &Kε = ×(0.2232) = 27775.8psi "1.15% 1.15 40000 0.15 Y = ×(0.2232 + 0.2232) = 30819psi Second Die 1.15 ! $ ! µ $ # 0.1 & #1+ & = #1+ & =1.477 π " α % # 12 × & " 180 % First Die "" 0.125+ 0.1118%% $$ '' " Daverage % # 2 & Φ =1+ 0.12$ ' =1+ 0.12$ ' =1.33 # Lcontact & $" 0.125− 0.1118%' $$ '' ## 2 ×sin12 && " % " µ % Ao σ d = ΦY $1+ 'ln$ ' =1.33× 27775.8×1.477× 0.2232 # α & # Af & σ d =12182.5psi π 2 Force = σ d × Af =12182.5× (0.1118) =119.6lb 4 Power =1.5HP = 825 ft − lb / s 825 ft − lb − s*0.9 Power = Force× velocity ⇒ v = = 6.2084 ft / s 119.6lb 2 2 ! Df $ ! 0.1118$ ventry = # & vexit = # & 6.2084 = 4.966 ft / s " DO % " 0.125 % Second Die "" 0.1118+ 0.10 %% $$ '' " Daverage % # 2 & Φ =1+ 0.12$ ' =1+ 0.12$ ' =1.35 # Lcontact & $" 0.1118− 0.10 %' $$ '' ## 2 ×sin12 && " % " µ % Ao σ d = ΦY $1+ 'ln$ ' =1.35×30819 ×1.477× 0.2232 # α & # Af & σ d =13720psi π 2 Force = σ d × Af =13720 × (0.10) =107.75lb 4 Power =1.5HP = 825 ft − lb / s 825 ft − lb − s*0.9 Power = Force× velocity ⇒ v = = 6.89 ft / s 107.75lb 2 2 ! Df $ ! 0.10 $ ventry = # & vexit = # & 6.89 = 5.51ft / s " DO % " 0.1118% Then, between the first and second die a wire storage drum is necessary. Calculate the power required for the second die if they exit speed aer the first die matches the entry speed of the second die. ! $2 2 DO ! 0.1118$ vexit = # & ventry = # & 6.2084 = 7.76 ft / s " Df % " 0.10 % Power =119.6lb × 7.76 ft / s = 928.1lb − ft / s Power90% =1.875HP Residual Stresses in Drawing Extrusion The metal is forced (squeeze) to flow through a die opening by compression forces to produce the desired shape.
Load more

Recommended publications
  • Influences of Different Die Bearing Geometries on the Wire-Drawing Process
    metals Article Influences of Different Die Bearing Geometries on the Wire-Drawing Process Gustavo Aristides Santana Martinez 1,*, Eduardo Ferro dos Santos 1 , Leonardo Kyo Kabayama 2 , Erick Siqueira Guidi 3 and Fernando de Azevedo Silva 3 1 Engineering School of Lorena, University of São Paulo-USP, Lorena 12602-810, Brazil; [email protected] 2 Institute of Mechanical Engineering, Federal University of Itajubá-UNIFEI, Itajubá 37500-903, Brazil; [email protected] 3 Guaratinguetá School of Engineering, Campus de Guaratinguetá,São Paulo State University-UNESP, 12516-410 Guaratinguetá, Brazil; [email protected] (E.S.G.); [email protected] (F.d.A.S.) * Correspondence: [email protected]; Tel.: +55-12-3159-5337 Received: 2 September 2019; Accepted: 8 October 2019; Published: 10 October 2019 Abstract: Metalworking is an essential process for the manufacture of machinery and equipment components. The design of the die geometry is an essential aspect of metalworking, and directly affects the resultant product’s quality and cost. As a matter of fact, a comprehensive understanding of the die bearing geometry plays a vital role in the die design process. For the specific case of wire drawing, however, few efforts have been dedicated to the study of the geometry of the bearing zone. In this regard, the present paper involves an attempt to investigate the effects of different geometries of the die bearing. For different forms of reduction as well as bearing zones, measurements are carried out for the wire-drawing process. Subsequently, by extracting the friction coefficients from the electrolytic tough pitch copper wire in cold-drawn essays, the numerical simulations are also implemented.
    [Show full text]
  • Friction and Stress Evaluation of Copper Wire Drawing Under Different Lubrication Conditions1
    ISSN 1516-392X FRICTION AND STRESS EVALUATION OF COPPER WIRE DRAWING UNDER DIFFERENT LUBRICATION CONDITIONS1 Antonio de Pádua Lima Filho2 Igor Ribeiro Ferreira3 Felipe Biava Cataneo4 Tiago Filipe Soares da Cunha5 André Mantovani6 Abstract ASTM C10100 W annealed copper wires with an initial diameter of 4.3 mm were drawn to a final diameter of 1.3 mm using a mineral oil lubricant of 0.06 Pa.s viscosity under hydrostatic pressures of approximately 35 MPa. Ten wire drawing dies (of 3.6 mm, 3.2 mm, 2.9 mm, 2.6 mm, 2.3 mm, 2.1 mm, 1.9 mm, 1.7 mm, 1.5 mm and 1.3 mm in diameter) were used to produce a total cross-sectional reduction of approximately 225%. Wire drawing forces under oil hydrostatic pressure with a graphite lubricant were compared to wire drawing forces without any lubricant. A measuring system was used to record the wire drawing forces over time and to study the frictional behaviour of the drawn wires. A wire drawing machine with a speed of 8 mm/s was used to verify the coefficient of friction fore wires drawn at low strain rates. Lubrication regimes were analysed for oil under hydrostatic pressure. The quasi-hydrodynamic regime ranged from 2.3 mm to 3.6 mm for the wire drawing die. An analytical model for calculating the wire drawing force/stress was developed to obtain the distribution of friction coefficients at each reduction of wire diameter. By controlling friction forces, it is possible to save energy and materials, as well as to determine the die replacement frequency.
    [Show full text]
  • Metal Extrusion and Drawing Processes and Equipment
    Hail University College of Engineering Department of Mechanical Engineering Metal Extrusion and Drawing Processes and Equipment Ch 15 Metal Extrusion and Drawing Extrusion and drawing involve, respectively, pushing or pulling a material through a die basically for the purpose of reducing or changing its cross-sectional area. Extrusion and drawing have numerous applications in the manufacture of continuous as well as discrete products from a wide variety of metals and alloys. In extrusion, a cylindrical billet is forced through a die in a manner similar to squeezing toothpaste from a tube or extruding Play-Doh ,in various cross sections in a toy press. Metal Extrusion Typical products made by extrusion are railings for sliding doors, window frames, tubing having various cross sections, aluminum ladder frames, and numerous structural and architectural shapes. Extrusions can be cut into desired lengths, which then become discrete parts, such as brackets, gears, and coat hangers Commonly extruded materials are aluminum, copper, steel, magnesium, and lead; other metals Depending on the ductility of the material, extrusion is carried out at room or elevated temperatures. Extrusion at room temperature often is combined with forging operations, in which case it generally is known as cold Extrusions and examples of products made by extrusion sectioning off extrusions Drawing In drawing, the cross section of solid rod, wire, or tubing is reduced or changed in shape by pulling it through a die. Drawn rods are used for shafts, spindles, and small pistons and as the raw material for fasteners (such as rivets, bolts, and screws). In addition to round rods, various profiles can be drawn.
    [Show full text]
  • Development Structural of a Wire Drawing and Extrusion Bench
    Modern Environmental Science and Engineering (ISSN 2333-2581) June 2018, Volume 4, No. 6, pp. 508-515 Doi: 10.15341/mese(2333-2581)/06.04.2018/003 Academic Star Publishing Company, 2018 www.academicstar.us Development Structural of A Wire Drawing and Extrusion Bench Gilmar Cordeiro da Silva, Ana Caroline de Souza Couto, Daniel de Castro Maciel, Alysson Lucas Vieira, Ernane Vinicius Silva, and Norberto Martins Pontifical University Catholic of Minas Gerais (PUC-MG), Brazil Abstract: The present work aim consist to design and construction of a drawing wire and extrusion bench able to perform the metal forming process by drawing and extrusion. The design of the structure as well as detailing of mechanical components were designed with the use of SOLIDWORS software and the simulation of structural strain (FEA - Finite Element Analysis) with the aid of ABAQUS/Standard software. Key words: wire drawing, extrusion, SOLIDWORKS, ABAQUS/Standard, finite element analysis any complex engineering problem can be reached by 1. Introduction subdividing the structure/component into smaller more Extrusion is the process by which a block of metal is manageable (finite) elements. The Finite Element reduced in cross-section by forcing it to flow through a Model (FEM) is analyzed with an inherently greater die orifice under high pressure. It is accepted practice precision than would otherwise be possible using to classify extrusion operation according to the conventional analyses, since the actual shape, load and direction relationships between the material flow and constraints, as well as material property combinations the punch movement. The basic extrusion operations can be specified with much greater accuracy.
    [Show full text]
  • High Carbon Wire Drawing
    High Carbon Wire Drawing Chemetall offers a fully integrated, innovative, and Increase your productivity optimized portfolio of products for cold forming. Our wire solutions arise from our comprehensive understanding of Extend die life. the challenges faced by wire producers. Faster start-up. Increase speed. We supply highly efficient and customized processes for Decrease temperatures. dip and in-line wire manufacturing. In addition, as part of Lower sludge. our dedication to our customers and to sustainability, we Reduce energy. offer advanced and original green options to reduce costs and environmental footprint. High Carbon Wire Drawing Discover our high-performance products and processes for dip and strand line processing for high carbon wire. The portfolio includes efficient cleaning and phosphate removal products, pickling inhibitors, activators, neutralizing agents, and phosphate-free pretreatment. Many state-of-the-art technologies, with and without nickel, for all types of wire manufacturing — from low-carbon to high-carbon iron and steel wire — are available. Energy-saving low temperature processes, high-performance zinc/calcium processes, and sludge-free electrolytic applications offer efficient, cost-effective, and environmentally responsible manufacturing, and benefit the downstream value chain. Learn about Gardo®, our full line of comprehensive solutions to improve productivity and quality. Activators Polymer Lubricants Salt Carriers Gardolene® V — Highly effective Gardomer® L — Gardolube ® SC — Lubricant activating rinse prior to the High performance lubricants to carriers to facilitate the cold forming application of zinc-phosphate. facilitate enhanced lubrication. of bare and phosphated iron and No heavy metal or mineral oil. steel wire, and stainless steel. Conversion Coatings Reactive Soaps Gardobond ® Z — Includes nickel-free zinc phosphate Gardolube ® L — A reactive soap conversion coatings designed used over zinc phosphate coatings.
    [Show full text]
  • Swaging and Wire Drawing
    Manufacturing Processes - 1 Prof. Inderdeep Singh Department of Mechanical & Industrial Engineering Indian Institute of Technology, Roorkee Module - 01 Lecture - 06 Swaging & Wire Drawing Very good morning to all of you, today we are going to start another important aspect of manufacturing technology, that is swaging and wire drawing. Before we start our discussion on swaging and wire drawing. We will have a brief overview of what we have discussed till date. We have had a series of lectures on manufacturing processes. We started our discussion with powder metallurgy. We had 3 lectures on powder metallurgy, after that we started our discussion on metal working or metal forming processes. In metal forming, we have had till now two lectures. In first lecture we discussed regarding the basic fundamental of metal working, in which we discussed plastic deformation, what is plastic deformation? How does plastic deformation takes place in metals? Then we discussed the various different types of metal working processes, just a brief overview. Later on we went on to discuss the relative advantages and disadvantages of hot warm and cold working processes. Then in the subsequent lecture, we started our discussion on various metal working operations. The first process that we discussed was forging. We saw that what are the various operations in forging? Like upset forging, precision forging, impression die forging, open die hammer forging, and auto forging. We saw what are the basic principles of these operations? And how where, and for what materials these operations can be applied? So, today we will discuss regarding the principle of swaging, the operation of swaging, and the operation of wire drawing.
    [Show full text]
  • Extrusion and Drawing
    Extrusion and Drawing IME 240/340 Extrusion • A billet, usually round, is forced through a die to create solid or hollow cross-sectional workpieces with elongated grain structures (preferred orientation) • Common analogy – squeezing toothpaste • A semi-continuous or batch process • At room temperature or elevated • Typical products: • Door & window frames • Tubing • Railings • Brackets • Metals, plastics, and coaxial (i.e. copper clad with silver) Figure 15.2 Extrusions, and examples of products made by sectioning off extrusions. Source: Kaiser Aluminum. indirect hydrostatic lateral Extrusion Processes Direct Extrusion Extrusion Parameters • Parameters include die angle (a), extrusion speed, billet temperature, and lubrication • Extrusion ratio, R = Ao/Af (typical values of 10 to 100) • Circumscribing Diameter (CCD) (for Aluminum 6 mm to 1 m, for steel up to 0.15 m A • Shape factor = Perimeter/CCD F A k ln o o • Extrusion constant, k Af • Typical lengths < 7.5 m Extrusion Die Design Figure 15.10 Poor and good examples of cross-sections to be extruded. Note the importance of eliminating sharp corners and of keeping section thicknesses uniform. Source: J. G. Bralla (ed.); Handbook of Product Design for Manufacturing. New York: McGraw-Hill Publishing Company, 1986. Used with permission. Hot Extrusion • For metals and alloys that do not have sufficient ductility at room temperature • Reduces forces • Increases die wear • Preheated billet will develop an abrasive oxide film that affects the material flow pattern, unless it is heated
    [Show full text]
  • Metal Forming Process
    METAL FORMING PROCESS Unit 1:Introduction and concepts Manufacturing Processes can be classified as i) Casting ii) Welding iii) Machining iv)Mechanical working v) Powder Metallurgy vi)Plastic Technology etc., In Mechanical working Process the raw material is converted to a given shape by the application of external force. The metal is subjected to stress.It is a process of changing the shape and size of the material under the influence of external force or stress.Plastic Deformation occurs. Classification of Metal Working Processes 1. General classification i. Rolling ii. Forging iii. Extrusion iv. Wire Drawing v. Sheet Metal Forming 2. Based on Temperature of Working i. Hot Working ii. Cold Working iii. Warm Working 3. Based on the applied stress i. Direct Compressive Stress ii. Indirect Compressive Stress iii. Tensile Stress iv. Bending Stress v. Shear Stress Classification of Metal Working based on temperature. Hot working: It is defined as the mechanical working of metal at an elevated (higher) temperature above a particular temperature. This temperature is referred to RCT(Re Crystallization Temperature). Cold Working: It is defined as the mechanical working of metal below RCT. Warm Working: It is defined as the mechanical working of metal at a temperature between that of Hot working and Cold Working. Ingot is the starting raw metal for all metal working process. Molten metal from the furnace is taken and poured into metallic moulds and allowed to cool or solidify. The cooled solid metal mass is then taken out of the mould. This solid metal is referred to as Ingot.This Ingot is later on converted to other forms by mechanical working.
    [Show full text]
  • Metal Forming Processes
    Metal Forming Processes Dr. Sunil Jha Introduction z Practically all metals, which are not used in cast form are reduced to some standard shapes for subsequent processing. Manufacturing companies producing metals supply metals in form of ingots which are obtained by casting liquid metal into a square cross section. Slab (500-1800 mm wide and 50-300 mm thick) Billets (40 to 150 sq mm) Blooms (150 to 400 sq mm) 1 Introduction Sometimes continuous casting methods are also used to cast the liquid metal into slabs, billets or blooms. These shapes are further processed through hot rolling, forging or extrusion, to produce materials in standard form such as plates, sheets, rods, tubes and structural sections. Sequence of operations for obtaining different shapes 2 Different Shapes Primary Metal Forming Processes z Rolling z Forging z Extrusion z Tube and wire drawing z and Deep drawing z Although Punching and Blanking operations are not metal forming processes however these will be covered due to similarity with deep drawing process. 3 Rolling Change in Grain Structure in Rolling 4 Rolling – Salient features z Rolling is the most extensively used metal forming process and its share is roughly 90% z The material to be rolled is drawn by means of friction into the two revolving roll gap z The compressive forces applied by the rolls reduce the thickness of the material or changes its cross sectional area z The geometry of the product depend on the contour of the roll gap Rolling – Salient features z Roll materials are cast iron, cast steel and forged steel because of high strength and wear resistance requirements z Hot rolls are generally rough so that they can bite the work, and cold rolls are ground and polished for good finish 5 Roll passes to get a 12 mm rod from 100 x 100 mm billet Roll configurations in rolling mills z Two-high and three-high mills are generally used for initial and intermediate passes during hot rolling, while four-high and cluster mills are used for final passes.
    [Show full text]
  • Extrusion, Wire Drawing, Tube Drawing and Making
    Extrusion, Wire Drawing, Tube Drawing and Making Extrusion is a process in which the metal is subjected to plastic flow by enclosing the metal in a closed chamber in which the only opening provided is through a die. The material is usually treated so that it can undergo plastic deformation at a sufficiently rapid rate and may be squeezed out of the hole in the die. In the process the metal assumes the opening provided in the die and comes out as a long strip with the same cross-section as the die-opening. Incidentally, the metal strip produced will have a longitudinal grain flow. The process of extrusion is most commonly used for the manufacture of solid and hollow sections of nonferrous metals and alloys. e.g. aluminum, aluminum-magnesium alloys, magnesium and its alloys, copper, brass and bronze etc. However, some steel products are also made by extrusion. The stock or the material to be extruded is in the shape of cast ingots or billets. Extrusion maybe done hot or cold. The cross-sections of extruded products vary widely. Some of these sections are shown in Fig. Some advantages of extrusion process are described below: (i) The complexity and range of parts which can be produced by extrusion process is very large. Dies are relative simple and easy to make. (ii) The extrusion process is complete in one pass only. This is not so in case of rolling, amount of reduction in extrusion is very large indeed. Extrusion process can be easily automated. (iii)Large diameter, hollow products, thin walled tubes etc.
    [Show full text]
  • 2. Technology Metal Forming
    2. Technology Metal Forming Technology: Metal Forming • Metal forming includes a large group of manufacturing processes in which plastic deformation is used to change the shape of metal work pieces • Plastic deformation: a permanent change of shape, i.e., the stress in materials is larger than its yield strength • Usually a die is needed to force deformed metal into the shape of the die Metal Forming • Metal with low yield strength and high ductility is in favor of metal forming • One difference between plastic forming and metal forming is Plastic: solids are heated up to be polymer melt Metal: solid state remains in the whole process 4 groups of forming techniques: • Rolling, • Forging & extrussion, • Wire drawing, • Deep drawing. Bars shaping vs. Sheets shaping Rolling Flat (plates) rolling Cross rolling slant rolling (for tubes production) Forging & extrussion Macroetched structure of a hot forged hook (a) Relative forgability for different metals and alloys. This information can be directly used for open die forgings. (b) Ease of die filling as a function of relative forability and flow stress/forging pressure – applicable to closed die forging Wire drawing In and conventional wire drawing process, the diameter of a rod or wire is reduced by pulling it through a conical die Illustration of some drawing operations: (a) conventional wire drawing with circular cross-section; (b) wire drawing with rectangular cross-section, using so-called ‘Turk’s’ head; (c) drawing using a floating mandrel. Sheet metal forming Equi-biaxial streching using a clamped sheet and a hemispherical punch (left) and a schematic of an industrial strech-forming operation (right).
    [Show full text]
  • New Tribo-Systems for Cold Forming of Steel, Stainless Steel and Aluminium Alloys
    Downloaded from orbit.dtu.dk on: Sep 26, 2021 New Tribo-systems for Cold Forming of Steel, Stainless Steel and Aluminium Alloys Bay, Niels Published in: Proceedings of 46th International Cold Forging Group (ICFG) Plenary Meeting Publication date: 2013 Document Version Publisher's PDF, also known as Version of record Link back to DTU Orbit Citation (APA): Bay, N. (2013). New Tribo-systems for Cold Forming of Steel, Stainless Steel and Aluminium Alloys. In Proceedings of 46th International Cold Forging Group (ICFG) Plenary Meeting [7-04] International Cold Forging Group. General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. Users may download and print one copy of any publication from the public portal for the purpose of private study or research. You may not further distribute the material or use it for any profit-making activity or commercial gain You may freely distribute the URL identifying the publication in the public portal If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. 46th ICFG Plenary Meeting Proceedings International Cold Forging Group New Tribo-systems for Cold Forming of Steel, Stainless Steel and Aluminium Alloys 1 N. Bay 1 Department of Mechanical Engineering, Technical University of Denmark, Denmark Abstract: Globalisation of industrial production and increasing demands for environmentally benign solutions has forced cold forging industry to search for new, economically optimized tribo-systems, which are less harmful to the working as well as the global environment.
    [Show full text]