2 Model Description
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

INP-10 (Catalogue of Indian Charts, Encs & Publications)
INP - 10 ROGR D A Y P H H I L C A O N F O F I I C T A E N INDIAN I N DIA Nautical Publications CATALOGUE OF INDIAN PAPER CHARTS ELECTRONIC NAVIGATIONAL CHARTS AND PUBLICATIONS Published by National Hydrographic Office, Dehradun Edition - 2021 INP 10 ROGR D A Y P H H I L C A O N F O F I I C T A E N I N DIA CATALOGUE OF PAPER CHARTS, ELECTRONICS NAVIGATIONAL CHARTS AND PUBLICATIONS NATIONAL HYDROGRAPHIC OFFICE DEHRADUN INDIA Jan 2021 CONTENTS INDEX PAGE Indian Ocean (Small Scale Charts) 1-2 Pakistan and West Coast of India (Sir Creek to Diu Head) 3-4 West Coast of India (Diu Head to Betul) 5-6 West Coast of India (Betul to Quilon and Lakshadweep) 7-8 South Coast of India and Sri Lanka 9-10 East Coast of India 11-12 Andaman and Nicobar Islands 13-14 Maldives, Mauritius and Seychelles Groups 15-16 Kenya, Tanzania and Mozambique 17-18 Myanmar, Thailand, Malaysia and Malacca Strait 19-20 Folios of IN Charts & Prices of Indian Hydrographic Charts and 21-22 Publications INDIAN OCEAN (SMALL SCALE CHARTS) Chart No. INT No. Chart Title Scale 1: Date of ENC Publication/ Released New Edition 21 Muscat to Mumbai 1 500000 1 5-A pr-201 8 Yes 22 752 Mumbai to Cape Comorin 1 500000 3 1 - J u l - 2 0 1 9 Yes 31 756 Bay of Bengal - Northern Portion (Krishnapatnam 1 500000 1 5-A pr-201 7 No to Bassein River) 32 754 Kochi (Cochin) to Visakhapatnam 1 500000 3 1 - J u l - 2 0 1 9 Yes 33 755 Bay of Bengal - Southern Portion 1 500000 31 -M ay-201 6 Yes 41 757 Andaman Sea 1 500000 1 5-D ec-201 0 Yes 7070 70 Indian Ocean Southern Part 10000000 1 5-M ar-201 9 No -

Indian Notices to Mariners
INDIAN NOTICES TO MARINERS EDITION NO. 05 DATED 01 MAR 2021 (CONTAINS NOTICES 070 TO 086) REACH US 24 x 7 [email protected] +91-135-2748373 [email protected] National Hydrographic Office Commander (H) 107-A, Rajpur Road Maritime Safety Information Services Dehradun – 248001 +91- 135 - 2746290-117 INDIA www.hydrobharat.gov.in CONTENTS Section No. Title I List of Charts Affected II Permanent Notices III Temporary and Preliminary Notices IV Marine Information V NAVAREA VIII Warnings inforce VI Corrections to Sailing Directions VII Corrections to List of Lights VIII Corrections to List of Radio Signals IX Reporting of Navigational Dangers ST TH (PUBLISHED ON NHO WEBSITE ON 1 & 16 OF EVERY MONTH) FEEDBACK: [email protected] INSIST ON INDIAN CHARTS AND PUBLICATIONS Original, Authentic and Up-to-Date © Govt. of India Copyright No permission is required to make copies of these Notices. However, such copies are not to be commercially sold. II MARINER’S OBLIGATION AND A CHART MAKER’S PLEA Observing changes at sea proactively and reporting them promptly to the concerned charting agency, is an obligation that all mariners owe to the entire maritime community towards SOLAS. Mariners are requested to notify the Chief Hydrographer to the Government of India at the above mentioned address/fax number/ E mail address immediately on discovering new or suspected dangers to navigation, changes/ defects pertaining to navigational aids, and shortcomings in Indian charts/ publications. The Hydrographic Note [Form IH – 102] is a convenient form to notify such changes. Specimen form is attached at Section IX with this notice. -

Indian Notices to Mariners
INDIAN NOTICES TO MARINERS EDITION NO. 08 DATED 16 APR 2020 (CONTAINS NOTICES 118 TO 124) REACH US 24 x 7 [email protected] +91-135-2748373 [email protected] National Hydrographic Office Commander (H) 107-A, Rajpur Road Maritime Safety Information Services Dehradun – 248001 +91- 135 - 2746290-117 INDIA www.hydrobharat.gov.in CONTENTS Section No. Title I List of Charts Affected II Permanent Notices III Temporary and Preliminary Notices IV Marine Information V NAVAREA VIII Warnings inforce VI Corrections to Sailing Directions VII Corrections to List of Lights VIII Corrections to List of Radio Signals IX Reporting of Navigational Dangers ST TH (PUBLISHED ON NHO WEBSITE ON 1 & 16 OF EVERY MONTH) FEEDBACK: [email protected] INSIST ON INDIAN CHARTS AND PUBLICATIONS Original, Authentic and Up-to-Date © Govt. of India Copyright No permission is required to make copies of these Notices. However, such copies are not to be commercially sold. II MARINER’S OBLIGATION AND A CHART MAKER’S PLEA Observing changes at sea proactively and reporting them promptly to the concerned charting agency, is an obligation that all mariners owe to the entire maritime community towards SOLAS. Mariners are requested to notify the Chief Hydrographer to the Government of India at the above mentioned address/fax number/ E mail address immediately on discovering new or suspected dangers to navigation, changes/ defects pertaining to navigational aids, and shortcomings in Indian charts/ publications. The Hydrographic Note [Form IH – 102] is a convenient form to notify such changes. Specimen form is attached at Section IX with this notice. -
Storage of Solar Power for Micro Grids in the Islands of Andaman
Storage of Solar power for Micro Grids in the Islands of Andaman & Nicobar, as well as Lakshadweep JOINT ELECTRICITY REGULATORY COMMISSION For the State of Goa and Union Territories These are Renewable Energy deficient areas (poor Capacity Utilization Factor & Low Solar Insolation). Further, these areas mostly being Coastal /Islands are tourist attraction and are having land constraint for Ground Mounted Solar Installation. Details of various areas under the jurisdiction of this Commission are: Sl. Location Latitude Longitude Remarks 1. Andaman & Nicobar 11.68° N 92.77° E Islands, Not Connected to National Grid, 1000 Kms from Mainland, Tourists place. The Power is Generated by Diesel and is thus very expensive. 2. Lakashadweep 10° 00' N 73.00° E Islands, Not Connected to National Grid, 300 Kms. from Mainland Tourists place. The Power is Generated by Diesel and is thus very expensive. Other Territories under the Jurisdiction of the Commission 3. Goa 15.4989° N 73.8278° E Coastal, Tourists Place 4. Chandigarh 30.75° N 76.78° E Non Coastal, Small Area, Pollution free area 5. Dadra & Nagar Haveli 20.27° N 73.02° E Highly Industrialized 95% Power Consumption by Industry, Highest Per Capita Power Consumption in India because of Industry 6.a Daman 20° 25' N 72°.53° E Coastal, High concentration of Industry 6.b Diu 20° 42' N 71.01° E Tourists Place, Coastal 7.a Puducherry- Puducherry 11.93° N 79.83° E Tourists, Coastal 7.b Karaikal- Puducherry 10° 55' N 79. 52° E Tourists, Coastal 7.c Mahe- Puducherry 11.7011° N 75.5367° E Tourists, Coastal 7.d Yanam- Puducherry 16.7333° N 82.25° E Tourists, Coastal The Joint Electricity Regulatory Commission (JERC) is pushing for Solar Roof Tops in all the seven territories. -
![05/21] ADMIRALTY Charts Affected by the Publication List](https://docslib.b-cdn.net/cover/5533/05-21-admiralty-charts-affected-by-the-publication-list-3135533.webp)
05/21] ADMIRALTY Charts Affected by the Publication List
I [05/21] ADMIRALTY Charts affected by the Publication List ADMIRALTY Charts ADMIRALTY Charts International Charts 177 8224 INT 1166 183 8248 INT 1354 410 8249 INT 1642 906 5124 (1) INT 1643 919 5124 (2) INT 5508 937 5124 (3) INT 13600 966 5124 (4) 1911 5124 (5) ADMIRALTY Publications 1951 5124 (6) 2026 5124 (7) NP 33 2172 5124 (8) e-NP 33 2292 5124 (9) NP 83 2738 5124 (10) NP 131 3490 5124 (11) NP 286(6) 8122 5124 (12) 8187 CP 1 8188 DE 1671 8189 DE 26 8200 IN 272 8201 IN 273 8202 SC 5623 UPDATE ON THE EFFECTS OF COVID-19 ON THE DELIVERY OF NAUTICAL PUBLICATIONS As a result of ongoing effects of COVID-19 on distribution infrastructure around the world, for safety reasons, we took the decision a few months ago to delay the publication of any non-essential ADMIRALTY Nautical Publications until further notice. We started to ease the restrictions on the dispatch of some of our paper publications for July 2020. We are continuing this effort and following some positive feedback on successful receipts of publications, we are now in a position to confirm the publications schedule for the rest of the year. As previously, we will continue to closely monitor our distribution network capacities. We reserve ourselves the right to amend this publications schedule accordingly should significant dispatch issues start arising again. WMO SURVEY The World Meteorological Organization is conducting a survey regarding the World-Wide Meteorological Information and Warning Service available at: WWW.JCOMM.INFO/MMMS Your participation is GREATLY appreciated and VALUED. -

Pseudanthias Marcia, a Marine Ornamental Fish
Pseudanthias marcia, a marine ornamental fish see page 7 Breakthrough in seed production of orange spotted grouper 3 Research Highlights 7 Training Programmes 14 Swachhta Pakhwada 17 Director speaks Awards 18 New Publications 18 Recreation Club 19 Visitors 19 Exhibitions 20 Warm greetings to all. Official Language Implementation 20 KVK (Ernakulam) News 21 rossing the last Programme Participations 22 quarter of 2016, it is Human Resources Development 24 C Contents Personnel 26 encouraging to note that several milestones have been Published by Dr. A. Gopalakrishnan crossed successfully and we Director are moving closer towards ICAR-Central Marine Fisheries Research Institute Post Box No. 1603, Ernakulam North P.O. the targets set in our Kochi - 682 018, Kerala, India Telephone: 0484-2394867 research activities. The Fax: 91-484-2394909 breakthrough in seed E-mail: [email protected] Website: www.cmfri.org.in production of orange Editor grouper, an important food fish, the successful captive broodstock Dr. U. Ganga development and larval rearing of a marine ornamental serranid are Editorial Committee critical first steps in building robust technologies for their culture in Dr. Rekha J. Nair controlled conditions in the future. Several training programmes Dr. R. Jeyabaskaran Shri. Subal Kumar Roul relevant to the needs of the stakeholders have also been organised Dr. N. S. Jeena and this can be further enhanced to reach the concerned Smt. P. Geetha Dr. K. A. Sajeela stakeholders. As we move into a New Year 2017 let the vision of a Shri. Aju K. Raju clean, healthy and vibrant marine fisheries sector in the country guide Assisted by and motivate our activities. -

Indian Notices to Mariners
INDIAN NOTICES TO MARINERS EDITION NO. 03 DATED 01 FEB 2021 (CONTAINS NOTICES 052 TO 059) REACH US 24 x 7 [email protected] +91-135-2748373 [email protected] National Hydrographic Office Commander (H) 107-A, Rajpur Road Maritime Safety Information Services Dehradun – 248001 +91- 135 - 2746290-117 INDIA www.hydrobharat.gov.in CONTENTS Section No. Title I List of Charts Affected II Permanent Notices III Temporary and Preliminary Notices IV Marine Information V NAVAREA VIII Warnings inforce VI Corrections to Sailing Directions VII Corrections to List of Lights VIII Corrections to List of Radio Signals IX Reporting of Navigational Dangers ST TH (PUBLISHED ON NHO WEBSITE ON 1 & 16 OF EVERY MONTH) FEEDBACK: [email protected] INSIST ON INDIAN CHARTS AND PUBLICATIONS Original, Authentic and Up-to-Date © Govt. of India Copyright No permission is required to make copies of these Notices. However, such copies are not to be commercially sold. II MARINER’S OBLIGATION AND A CHART MAKER’S PLEA Observing changes at sea proactively and reporting them promptly to the concerned charting agency, is an obligation that all mariners owe to the entire maritime community towards SOLAS. Mariners are requested to notify the Chief Hydrographer to the Government of India at the above mentioned address/fax number/ E mail address immediately on discovering new or suspected dangers to navigation, changes/ defects pertaining to navigational aids, and shortcomings in Indian charts/ publications. The Hydrographic Note [Form IH – 102] is a convenient form to notify such changes. Specimen form is attached at Section IX with this notice. -

This Is Practice Test on Indian Geography Time Allowed Is 9.30 to 11 Hrs
This is Practice Test on Indian Geography Time allowed is 9.30 to 11 hrs. Correct answers 75 x 2 = 150 marks. Each incorrect answer carries a negative marking of o. 33%, which means for every wrong answer 0.66 marks will be deducted ˜ ˜ ˜ 1. Match the following Hydro Power Projects State i) Birla Sui a) Himachal ii) Dhauliganga b) Uttrakhand iii) Indira Sagar c) Madhya Pradesh iv) Loktak d) Manipur a) i-d, ii-b, iii-c, iv-a b) i-b, ii-c, iii-a, iv-d c) i-a, ii-b, iii-c, iv-d d)None 2. Match the following Hydro Power Project River i) Loktak a) Sutlej ii) Omkareshwar b) Chenab iii) Baglihar c) Narmada iv) Nathpa Jhakri d) Loktak Lake a) i-d, ii-c, iii-b, iv-a b) i-c, ii-d, iii-b, iv-a c) i-d, ii-c, iii-b, iv-a d)None 3. Consider the following, which of these are correct? i) The largest power station in India is in Tarapur Maharashtra ii) The largest reactor is Dhruva at the Babha Atomic Resarch Center. iii) Currently India is using two types of Power reactors, Pressurized Heavy Water Reactor and the Boiling Water Reactor. a) i and ii b) ii and iii c) i and iii d) All of the above 4. Consider the following 1. Aravallis 2. Vindhayas 3. Thar Desert 4. Satpuras Which of the following extend over the state of Gujarat? (a) 1 and 4 Only (b) 1, 2 and 4 only (c) 2, 3 and 4 only (d) All of the above 5. -
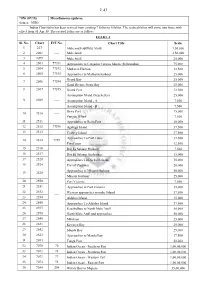
*076 (07/18) Miscellaneous Updates. Source: NHO. Indian Chart Folio Has Been Revised from Existing 7 Folios to 6 Folios
2. 43 *076 (07/18) Miscellaneous updates. Source: NHO. Indian Chart folio has been revised from existing 7 folios to 6 folios. The revised folios will come into force with effect from 01 Apr 18. The revised folios are as follow: FOLIO -1 Sl. No. Chart INT No. Chart Title Scale 1 227 Male and Fadiffolu Atolls 1,50,000 2 2061 ---- Male Atoll 1,50,000 3 2099 Male Atoll 25,000 4 2503 77391 Approaches to Cargados Carajos Shoals (St Brandon) 75,000 5 2504 77392 Mathurin Harbour 12,500 6 2505 77393 Approaches to Mathurin harbour 25,000 Grand Bay 25,000 7 2506 77394 Gand Riviere Noire Bay 25,000 8 2507 77395 Grand Port 12,500 Assumption Island (Seychelles) 25,000 9 2509 ---- Assumption Island - A 7,500 Assumption Island - B 7,500 Beira Port 15,000 10 2510 ---- Pungoe Wharf 7,500 11 2511 Approaches to Beira Port 20,000 12 2512 77396 Agalega Island 37,500 13 2513 Coetivy Island 37,500 Approaches To Port Louis 37,500 14 2514 7739 Port Louis 12,500 15 2516 Dar Es Salaam Harbour 7,500 16 2517 Dar Es Salaam Anchorage 15,000 17 2520 Approaches To Dar Es Salaam 30,000 18 2524 Port of Zanzibar 20,000 Approaches to Mkoani Harbour 50,000 19 2528 Mkoani Harbour 25,000 20 2550 Port Victoria 7,500 21 2551 Approaches to Port Victoria 35,000 22 2552 Western approaches to mahe Island 37,500 ---- 23 2554 Aldabra Island 15,000 24 2555 Approaches To Aldabra Island 37,500 25 2597 Kaashidhoo to North Male Atoll 50,000 26 2598 North Male Atoll and approaches 50,000 27 2640 Mkokoni 25,000 28 2641 Kiwaiyu Bay 25,000 29 2642 Manda Bay 25,000 30 2643 Approaches to Manda Bay 37,500 31 2693 Tanga Port 50,000 32 7070 70 Indian Ocean - Southern Part 1,00,00,000 33 7071 71 Indian Ocean - Northern Part 1,00,00,000 34 7072 72 Indian Ocean - Western Part 1,00,00,000 35 7073 73 Indian Ocean - Eastern Part 1,00,00,000 36 7204 204 Walvis Bay to Maputo 35,00,000 2. -

Indian Notices to Mariners
INDIAN NOTICES TO MARINERS EDITION NO. 05 DATED 01 MAR 2020 (CONTAINS NOTICES 078 TO 094) REACH US 24 x 7 [email protected] +91-135-2748373 [email protected] National Hydrographic Office Commander (H) 107-A, Rajpur Road Maritime Safety Information Services Dehradun – 248001 +91- 135 - 2746290-117 INDIA www.hydrobharat.gov.in CONTENTS Section No. Title I List of Charts Affected II Permanent Notices III Temporary and Preliminary Notices IV Marine Information V NAVAREA VIII Warnings inforce VI Corrections to Sailing Directions VII Corrections to List of Lights VIII Corrections to List of Radio Signals IX Reporting of Navigational Dangers ST TH (PUBLISHED ON NHO WEBSITE ON 1 & 16 OF EVERY MONTH) FEEDBACK: [email protected] INSIST ON INDIAN CHARTS AND PUBLICATIONS Original, Authentic and Up-to-Date © Govt. of India Copyright No permission is required to make copies of these Notices. However, such copies are not to be commercially sold. II MARINER’S OBLIGATION AND A CHART MAKER’S PLEA Observing changes at sea proactively and reporting them promptly to the concerned charting agency, is an obligation that all mariners owe to the entire maritime community towards SOLAS. Mariners are requested to notify the Chief Hydrographer to the Government of India at the above mentioned address/fax number/ E mail address immediately on discovering new or suspected dangers to navigation, changes/ defects pertaining to navigational aids, and shortcomings in Indian charts/ publications. The Hydrographic Note [Form IH – 102] is a convenient form to notify such changes. Specimen form is attached at Section IX with this notice. -

Status of Fisheries of Lakshadweep
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by CMFRI Digital Repository ISSN 0254-380 X MARINE FISHERIES INFORMATION SERVICE No. 187 January, February, March, 2006 TECHNICAL AND EXTENSION SERIES CENTRAL MARINE FISHERIES RESEARCH INSTITUTE COCHIN, INDIA (INDIAN COUNCIL OF AGRICULTURAL RESEARCH) Mar. Fish. Infor. Serv., T&E Ser., No. 187, 2006 1 1158 Status of fisheries of Lakshadweep The Union Territory of Lakshadweep (08 Except Androth, all the islands have 00'N and 12 30'N latitudes and 71 00'E and lagoon, some of which are fast getting 74 00'E longitudes), consisting of eleven filled up by calcareous sand. Bitra has inhabited and 25 uninhabited islands, is perhaps the most magnificent lagoon. scattered in the Arabian Sea at about 200- Minicoy has a large and deep lagoon with 400 km from the Malabar Coast. Coconut a boat channel on the northern side giving and fish form the mainstay of the economy safe access and anchorage to vessels of of the islanders. The islands became a about 3 m draught. Union Territory of India in 1956 and it was The outer edges of atolls drop precipitously named Lakshadweep in 1973. Since then to the ocean floor. Mostly on the eastern there has been rapid progress especially in side the atolls overhang the precipitous the fields of agriculture, fisheries, shelf. The eastern side is generally more education, health etc. Next in importance sheltered from wind and current. The to agriculture, the fisheries sector plays an islands, ranging in area from 1 ha to nearly important role in the economy of the 440 ha are little specks in the Indian Ocean. -

Marine Oct-Dec-Eng
ISSN 0254-380 X MARINE FISHERIES INFORMATION SERVICE No. 187 January, February, March, 2006 TECHNICAL AND EXTENSION SERIES CENTRAL MARINE FISHERIES RESEARCH INSTITUTE COCHIN, INDIA (INDIAN COUNCIL OF AGRICULTURAL RESEARCH) The Marine Fisheries Information Service : Technical and Extension Series envisages dissemination of information on marine fishery resources based on research results to the planners, industry and fish farmers, and transfer of technology from laboratory to field. Abbreviation - Mar. Fish. Infor. Serv., T & E Ser., No. 187, January, February, March, 2006 CONTENTS Article No. Article Title Pages 1158 Status of fisheries of Lakshadweep ............................................................................................ 1 1159 Impact of coastal bottom trawling on target and non- target resources along the south west coast of India ........................................................................................................................................ 7 1160 Report on the first occurrence of Bathynomus giganteus, a deep sea isopod from the west coast of India ...................................................................................................................................... 13 1161 Trends in the landings of Sepia aculeata and Sepia prashadi at Mumbai, Maharashtra. ........ 15 1162 On the first record of a rare marine ornamental fish from the Gulf of Mannar ...................... 17 1163 A note on the landing of a slender sunfish near Rameswaram ................................................