DOCSLIB.ORG

Transformations General Transformations Affine

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Transformations General Transformations Affine Transformations General Transformations Objectives A transformation maps points to other points and/or vectors to other vectors • Introduce standard transformations - Rotation v=T(u) -Translation -Scaling - Shear • Derive homogeneous coordinate Q=T(P) transformation matrices • Learn to build arbitrary transformation matrices from simple transformations Angel: Interactive Computer Graphics 4E © Addison-Wesley 2005 1 Angel: Interactive Computer Graphics 4E © Addison-Wesley 2005 2 Affine Transformations Pipeline Implementation • Line preserving • Characteristic of many physically T (from application program) important transformations frame - Rigid body transformations: rotation, translation u T(u) buffer - Scaling, shear transformation rasterizer v T(v) T(v) • Importance in graphics is that we need T(v) only transform endpoints of line segments v T(u) and let implementation draw line segment u T(u) between the transformed endpoints vertices vertices pixels Angel: Interactive Computer Graphics 4E © Addison-Wesley 2005 3 Angel: Interactive Computer Graphics 4E © Addison-Wesley 2005 4 1 Notation Translation We will be working with both coordinate-free • Move (translate, displace) a point to a representations of transformations and new location representations within a particular frame P’ P,Q, R: points in an affine space u, v, w: vectors in an affine space d α, β, γ: scalars P p, q, r: representations of points -array of 4 scalars in homogeneous coordinates • Displacement determined by a vector d u, v, w: representations of points - Three degrees of freedom -array of 4 scalars in homogeneous coordinates -P’=P+d Angel: Interactive Computer Graphics 4E © Addison-Wesley 2005 5 Angel: Interactive Computer Graphics 4E © Addison-Wesley 2005 6 Translation Using How many ways? Representations Although we can move a point to a new location Using the homogeneous coordinate in infinite ways, when we move many points representation in some frame there is usually only one way p=[ x y z 1]T p’=[x’ y’ z’ 1]T d=[dx dy dz 0]T Hence p’ = p + d or x’=x+dx note that this expression is in y’=y+d four dimensions and expresses y point = vector + point object translation: every point displaced z’=z+d by same vector z Angel: Interactive Computer Graphics 4E © Addison-Wesley 2005 7 Angel: Interactive Computer Graphics 4E © Addison-Wesley 2005 8 2 Translation Matrix Rotation (2D) We can also express translation using a Consider rotation about the origin by θ degrees 4 x 4 matrix T in homogeneous coordinates - radius stays the same, angle increases by θ p’=Tp where x’ = r cos (φ + θ) ⎡1 0 0 d ⎤ x y’ = r sin (φ + θ) ⎢0 1 0 d ⎥ ⎢ y ⎥ T = T(dx, dy, dz) = ⎢0 0 1 dz ⎥ x’= x cos θ – y sin θ ⎢ ⎥ y’ = x sin θ + y cos θ ⎣0 0 0 1 ⎦ This form is better for implementation because all affine transformations can be expressed this way and x = r cos φ multiple transformations can be concatenated together y = r sin φ Angel: Interactive Computer Graphics 4E © Addison-Wesley 2005 9 Angel: Interactive Computer Graphics 4E © Addison-Wesley 2005 10 Rotation about the z axis Rotation Matrix • Rotation about z axis in three dimensions leaves all points with the same z - Equivalent to rotation in two dimensions in ⎡cos θ − sin θ 0 0⎤ planes of constant z ⎢ ⎥ R = R (θ) = sin θ cos θ 0 0 x’=x cos θ –y sin θ z ⎢ ⎥ y’ = x sin θ + y cos θ ⎢ 0 0 1 0⎥ z’ =z ⎢ ⎥ ⎣ 0 0 0 1⎦ - or in homogeneous coordinates p’=Rz(θ)p Angel: Interactive Computer Graphics 4E © Addison-Wesley 2005 11 Angel: Interactive Computer Graphics 4E © Addison-Wesley 2005 12 3 Rotation about x and y axes Scaling • Same argument as for rotation about z axis Expand or contract along each axis (fixed point of origin) - For rotation about x axis, x is unchanged x’=sxx - For rotation about y axis, y is unchanged y’=syx ⎡1 0 0 0⎤ z’=szx ⎢0 cos θ - sin θ 0⎥ ⎢ ⎥ p’=Sp R = Rx(θ) = ⎢0 sin θ cos θ 0⎥ ⎢ ⎥ ⎣0 0 0 1⎦ ⎡sx 0 0 0⎤ ⎢ ⎥ ⎡ cos θ 0 sin θ 0⎤ 0 sy 0 0 S = S(sx, sy, sz) = ⎢ ⎥ ⎢ 0 1 0 0⎥ R = R (θ) = ⎢ ⎥ ⎢ 0 0 sz 0⎥ y ⎢ ⎥ ⎢- sin θ 0 cos θ 0⎥ 0 0 0 1 ⎢ ⎥ ⎣ ⎦ ⎣ 0 0 0 1⎦ Angel: Interactive Computer Graphics 4E © Addison-Wesley 2005 13 Angel: Interactive Computer Graphics 4E © Addison-Wesley 2005 14 Reflection Inverses Corresponds to negative scale factors • Although we could compute inverse matrices by general formulas, we can use simple geometric observations s = -1 s = 1 original -1 x y - Translation: T (dx, dy, dz) = T(-dx, -dy, -dz) - Rotation: R -1(θ) = R(-θ) • Holds for any rotation matrix • Note that since cos(-θ) = cos(θ) and sin(-θ)=-sin(θ) R -1(θ) = R T(θ) sx = -1 sy = -1 sx = 1 sy = -1 -1 - Scaling: S (sx, sy, sz) = S(1/sx, 1/sy, 1/sz) Angel: Interactive Computer Graphics 4E © Addison-Wesley 2005 15 Angel: Interactive Computer Graphics 4E © Addison-Wesley 2005 16 4 Concatenation Order of Transformations • We can form arbitrary affine transformation • Note that matrix on the right is the first matrices by multiplying together rotation, applied translation, and scaling matrices • Mathematically, the following are • Because the same transformation is applied to equivalent many vertices, the cost of forming a matrix p’ = ABCp = A(B(Cp)) M=ABCD is not significant compared to the cost of computing Mp for many vertices p • Note many references use column matrices to represent points. In terms of • The difficult part is how to form a desired transformation from the specifications in the column matrices application p’T = pTCTBTAT Angel: Interactive Computer Graphics 4E © Addison-Wesley 2005 17 Angel: Interactive Computer Graphics 4E © Addison-Wesley 2005 18 General Rotation About Rotation About a Fixed the Origin Point other than the Origin Move fixed point to origin A rotation by θ about an arbitrary axis can be decomposed into the concatenation Rotate of rotations about the x, y, and z axes Move fixed point back M = T(pf) R(θ) T(-pf) R(θ) = Rz(θz) Ry(θy) Rx(θx) y θ v θx θy θz are called the Euler angles Note that rotations do not commute x We can use rotations in another order but with different angles z Angel: Interactive Computer Graphics 4E © Addison-Wesley 2005 19 Angel: Interactive Computer Graphics 4E © Addison-Wesley 2005 20 5 Instancing Shear • In modeling, we often start with a simple • Helpful to add one more basic transformation object centered at the origin, oriented with • Equivalent to pulling faces in opposite directions the axis, and at a standard size • We apply an instance transformation to its vertices to Scale Orient Locate Angel: Interactive Computer Graphics 4E © Addison-Wesley 2005 21 Angel: Interactive Computer Graphics 4E © Addison-Wesley 2005 22 Shear Matrix Consider simple shear along x axis x’ = x + y cot θ y’ = y z’ = z ⎡1 cot θ 0 0⎤ ⎢0 1 0 0⎥ H(θ) = ⎢ ⎥ ⎢0 0 1 0⎥ -1 ⎢ ⎥ H (θ) = H(-θ) ⎣0 0 0 1⎦ Angel: Interactive Computer Graphics 4E © Addison-Wesley 2005 23 6.
Load more

Recommended publications
  • Systems Analysis of Stochastic and Population Balance Models for Chemically Reacting Systems
    Systems Analysis of Stochastic and Population Balance Models for Chemically Reacting Systems by Eric Lynn Haseltine A dissertation submitted in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY (Chemical Engineering) at the UNIVERSITY OF WISCONSIN–MADISON 2005 c Copyright by Eric Lynn Haseltine 2005 All Rights Reserved i To Lori and Grace, for their love and support ii Systems Analysis of Stochastic and Population Balance Models for Chemically Reacting Systems Eric Lynn Haseltine Under the supervision of Professor James B. Rawlings At the University of Wisconsin–Madison Chemical reaction models present one method of analyzing complex reaction pathways. Most models of chemical reaction networks employ a traditional, deterministic setting. The short- comings of this traditional framework, namely difficulty in accounting for population het- erogeneity and discrete numbers of reactants, motivate the need for more flexible modeling frameworks such as stochastic and cell population balance models. How to efficiently use models to perform systems-level tasks such as parameter estimation and feedback controller design is important in all frameworks. Consequently, this thesis focuses on three main areas: 1. improving the methods used to simulate and perform systems-level tasks using stochas- tic models, 2. formulating and applying cell population balance models to better account for experi- mental data, and 3. applying moving-horizon estimation to improve state estimates for nonlinear reaction systems. For stochastic models, we have derived and implemented techniques that improve simulation efficiency and perform systems-level tasks using these simulations. For discrete stochastic models, these systems-level tasks rely on approximate, biased sensitivities, whereas continuous models (i.e.
    [Show full text]
  • Opengl Transformations
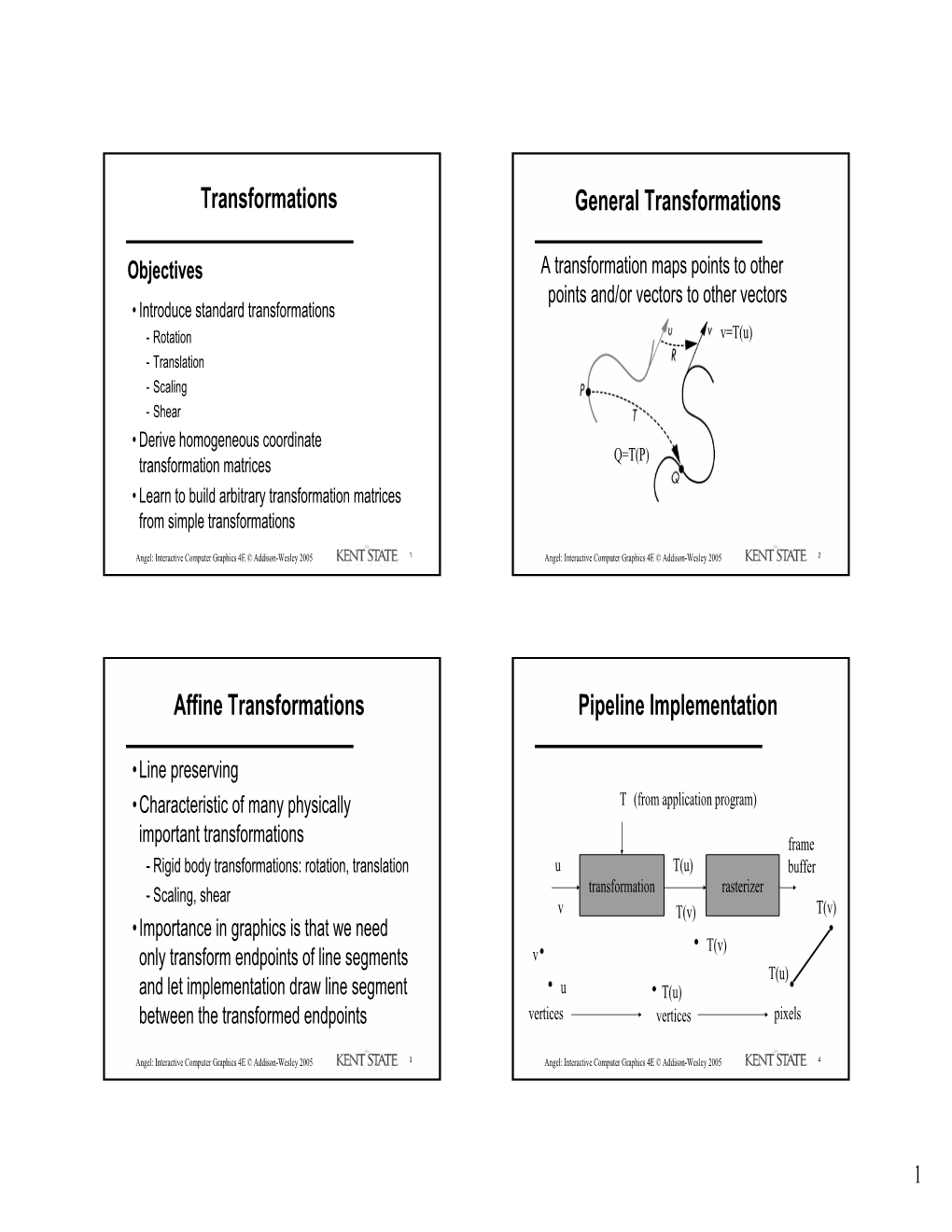
    Transformations CS 537 Interactive Computer Graphics Prof. David E. Breen Department of Computer Science E. Angel and D. Shreiner: Interactive Computer Graphics 6E © Addison-Wesley 2012 1 Objectives • Introduce standard transformations - Rotation - Translation - Scaling - Shear • Derive homogeneous coordinate transformation matrices • Learn to build arbitrary transformation matrices from simple transformations E. Angel and D. Shreiner: Interactive Computer Graphics 6E © Addison-Wesley 2012 2 General Transformations A transformation maps points to other points and/or vectors to other vectors v=T(u) Q=T(P) E. Angel and D. Shreiner: Interactive Computer Graphics 6E © Addison-Wesley 2012 3 Affine Transformations • Line preserving • Characteristic of many physically important transformations - Rigid body transformations: rotation, translation - Scaling, shear • Importance in graphics is that we need only transform endpoints of line segments and let implementation draw line segment between the transformed endpoints E. Angel and D. Shreiner: Interactive Computer Graphics 6E © Addison-Wesley 2012 4 Pipeline Implementation T (from application program) frame u T(u) buffer transformation rasterizer v T(v) T(v) v T(v) T(u) u T(u) vertices vertices pixels E. Angel and D. Shreiner: Interactive Computer Graphics 6E © Addison-Wesley 2012 5 Notation We will be working with both coordinate-free representations of transformations and representations within a particular frame P,Q, R: points in an affine space u, v, w: vectors in an affine space α, β, γ: scalars p, q, r: representations of points -array of 4 scalars in homogeneous coordinates u, v, w: representations of vectors -array of 4 scalars in homogeneous coordinates E. Angel and D. Shreiner: Interactive Computer Graphics 6E © Addison-Wesley 2012 6 Translation • Move (translate, displace) a point to a new location P’ d P • Displacement determined by a vector d - Three degrees of freedom - P’= P+d E.
    [Show full text]
  • Affine Transforms and Matrix Algebra
    Chapter 5 Matrix Algebra and Affine Transformations 5.1 The need for multiple coordinate frames So far we have been dealing with cameras, lights and geometry in our scene by specifying everything with respect to a common origin and coordinate system. This turns out to be very limiting. For example, for animation we will want to be able to move the camera and models and render a sequence of images as time advances to create an illusion of motion. We may wish to build models separately and then combine them together to make a scene. We may wish to define one object relative to another { for example we may want to place a hand at the end of an arm. In order to provide this flexibility we need a good mechanism to provide for multiple coordinate systems and for easy transformation between them. We will call these coordinate systems, which we use to represent a scene, coordinate frames. Figure 5.1 shows an example of what we mean. A cylinder has been built in its own modeling coordinate frame and then rotated and translated into the entire scene's coordinate frame. The set of operations providing for all transformations such as these, are known as the affine transforms. The affines include translations and all linear transformations, like scale, rotate, and shear. 29 30CHAPTER 5. MATRIX ALGEBRA AND AFFINE TRANSFORMATIONS m o Cylinder in model Cylinder in world frame O. The coordinates M. cylinder has been rotated and translated. Figure 5.1: Object in model and world coordinate frames. 5.2 Affine transformations Let us first examine the affine transforms in 2D space, where it is easy to illustrate them with diagrams, then later we will look at the affines in 3D.
    [Show full text]
  • Part IA — Vectors and Matrices
    Part IA | Vectors and Matrices Based on lectures by N. Peake Notes taken by Dexter Chua Michaelmas 2014 These notes are not endorsed by the lecturers, and I have modified them (often significantly) after lectures. They are nowhere near accurate representations of what was actually lectured, and in particular, all errors are almost surely mine. Complex numbers Review of complex numbers, including complex conjugate, inverse, modulus, argument and Argand diagram. Informal treatment of complex logarithm, n-th roots and complex powers. de Moivre's theorem. [2] Vectors 3 Review of elementary algebra of vectors in R , including scalar product. Brief discussion n n of vectors in R and C ; scalar product and the Cauchy-Schwarz inequality. Concepts of linear span, linear independence, subspaces, basis and dimension. Suffix notation: including summation convention, δij and "ijk. Vector product and triple product: definition and geometrical interpretation. Solution of linear vector equations. Applications of vectors to geometry, including equations of lines, planes and spheres. [5] Matrices Elementary algebra of 3 × 3 matrices, including determinants. Extension to n × n complex matrices. Trace, determinant, non-singular matrices and inverses. Matrices as linear transformations; examples of geometrical actions including rotations, reflections, dilations, shears; kernel and image. [4] Simultaneous linear equations: matrix formulation; existence and uniqueness of solu- tions, geometric interpretation; Gaussian elimination. [3] Symmetric, anti-symmetric, orthogonal, hermitian and unitary matrices. Decomposition of a general matrix into isotropic, symmetric trace-free and antisymmetric parts. [1] Eigenvalues and Eigenvectors Eigenvalues and eigenvectors; geometric significance. [2] Proof that eigenvalues of hermitian matrix are real, and that distinct eigenvalues give an orthogonal basis of eigenvectors.
    [Show full text]
  • Characteristic Polynomials of P-Adic Matrices
    Characteristic polynomials of p-adic matrices Xavier Caruso David Roe Tristan Vaccon Université Rennes 1 University of Pittsburg Université de Limoges [email protected] [email protected] [email protected] ABSTRACT and O˜(n2+ω/2) operations. Second, while the lack of divi- N We analyze the precision of the characteristic polynomial sion implies that the result is accurate modulo p as long as Z χ(A) of an n × n p-adic matrix A using differential pre- M ∈ Mn( p), they still do not yield the optimal precision. cision methods developed previously. When A is integral A faster approach over a field is to compute the Frobe- N nius normal form of M, which is achievable in running time with precision O(p ), we give a criterion (checkable in time ω O˜(nω)) for χ(A) to have precision exactly O(pN ). We also O˜(n ) [15]. However, the fact that it uses division fre- give a O˜(n3) algorithm for determining the optimal preci- quently leads to catastrophic losses of precision. In many sion when the criterion is not satisfied, and give examples examples, no precision remains at the end of the calcula- when the precision is larger than O(pN ). tion. Instead, we separate the computation of the precision CCS Concepts of χM from the computation of an approximation to χM . Given some precision on M, we use [3, Lem. 3.4] to find the •Computing methodologies → Algebraic algorithms; best possible precision for χM . The analysis of this preci- Keywords sion is the subject of much of this paper.
    [Show full text]
  • Equivalence of Matrices
    Equivalence of Matrices Math 542 May 16, 2001 1 Introduction The first thing taught in Math 340 is Gaussian Elimination, i.e. the process of transforming a matrix to reduced row echelon form by elementary row operations. Because this process has the effect of multiplying the matrix by an invertible matrix it has produces a new matrix for which the solution space of the corresponding linear system is unchanged. This is made precise by Theorem 2.4 below. The theory of Gaussian elimination has the following features: 1. There is an equivalence relation which respects the essential properties of some class of problems. Here the equivalence relation is called row equivalence by most authors; we call it left equivalence. 2. The equivalence classes of this relation are the orbits of a group action. In the case of left equivalence the group is the general linear group acting by left multiplication. 3. There is a characterization of the equivalence relation in terms of some invariant (or invariants) associated to a matrix. In the case of left equivalence the characterization is provided by Theorem 2.4 which says that two matrices of the same size are left equivalent if and only if they have the same null space. 4. There is a normal form and a theorem which says that each matrix is equivalent to a unique matrix in normal form. In the case of left equivalence the normal form is reduced row echelon form (not explained in this paper). 1 Our aim in this paper is to give other examples of equivalence relations which fit this pattern.
    [Show full text]
  • A Fast Algorithm for General Raster Rotation
    - 77 - A FAST ALGORITHM FOR GENERAL RASTER ROTATION Ala" W. Paeth Computer Graphics Laboratory, Department of Computer Science University of Waterloo, Waterloo, Ontario, Canada N2L 3G1 Tel: (519) 888-4534, E-Mail: A WPaeth%[email protected] ABSTRACT INTRODUCI10N The rotation of a digitized raster by an arbitrary angle We derive a high-speed raster rotation algorithm is an essential function for many raster manipulation based on the decomposition of a 2-D rotation matrix systems. We derive and implement a particularly fast into the product of three shear matrices. Raster algorithm which rotates (with scaling invariance) rasters shearing is done on a scan-line basis, and is particularly arbitrarily; skewing and translation of the raster is also efficient. A useful shearing approximation is averaging made possible by the implementation. This operation is adjacent pixels, where the blending ratios remain conceptually simple, and is a good candidate for constant for each scan-line. Taken together, our inclusion in digital paint or other interactive systems, technique rotates (with anti-aliasing) rasters faster than where near real-time performance is required. previous methods. The general derivation of rotation also sheds light on two common techniques: small angle RESUME rotation using a two-pass algorithm, and three-pass 9O-degree rotation. We also provide a comparative La rotation d'un "raster" d'un angle arbitraire est une analysis of Catmull and Smith's method [Catm80n and foilction essentielle de plusieurs logiciels de a discussion of implementation strategies on frame manipulation de "raster". Nous avons implemente un buffer hardware. algorithme rapide de rotation de "raster" conservant l'echelle de I'image.
    [Show full text]
  • Practical Linear Algebra: a Geometry Toolbox Fourth Edition Chapter 5: 2 2 Linear Systems ×
    Practical Linear Algebra: A Geometry Toolbox Fourth Edition Chapter 5: 2 2 Linear Systems × Gerald Farin & Dianne Hansford A K Peters/CRC Press www.farinhansford.com/books/pla c 2021 Farin & Hansford Practical Linear Algebra 1 / 50 Outline 1 Introduction to 2 2 Linear Systems × 2 Skew Target Boxes Revisited 3 The Matrix Form 4 A Direct Approach: Cramer’s Rule 5 Gauss Elimination 6 Pivoting 7 Unsolvable Systems 8 Underdetermined Systems 9 Homogeneous Systems 10 Kernel 11 Undoing Maps: Inverse Matrices 12 Defining a Map 13 Change of Basis 14 Application: Intersecting Lines 15 WYSK Farin & Hansford Practical Linear Algebra 2 / 50 Introduction to 2 2 Linear Systems × Two families of lines are shown Intersections of corresponding line pairs marked For each intersection: solve a 2 × 2 linear system Farin & Hansford Practical Linear Algebra 3 / 50 Skew Target Boxes Revisited Geometry of a 2 2 system × a1 and a2 define a skew target box Given b with respect to the [e1, e2]-system: What are the components of b with respect to the [a1, a2]-system? 2 4 4 a = , a = , b = 1 1 2 6 4 2 1 4 4 1 + = × 1 2 × 6 4 Farin & Hansford Practical Linear Algebra 4 / 50 Skew Target Boxes Revisited Two equations in the two unknowns u1 and u2 2u1 + 4u2 = 4 u1 + 6u2 = 4 Solution: u1 = 1 and u2 = 1/2 This chapter dedicated to solving these equations Farin & Hansford Practical Linear Algebra 5 / 50 The Matrix Form Two equations a1,1u1 + a1,2u2 = b1 a2,1u1 + a2,2u2 = b2 Also called a linear system a a u b 1,1 1,2 1 = 1 a2,1 a2,2u2 b2 Au = b u called the solution of linear
    [Show full text]
  • 1. Which of the Following Could Relate to Determinants? A) Invertibility of A
    1. Which of the following could relate to determinants? a) invertibility of a 2 × 2 matrix b) determinant 1 (or -1) coding matrix with integer entries will ensure we don’t pick up fractions in the decoding matrix c) both of the above http://www.mathplane.com/gate_dwebcomics/math_comics_archive_spring_2017 Dr. Sarah i-clickers in 1.8, 1.9, 2.7 2. Which of the following matrices does not have an inverse? 1 2 a) 3 4 2 2 b) 4 4 0 4 c) 2 0 d) more than one do not have inverses e) all have inverses Cayley’s [1855] introductory paper in matrix theory introduces... the ideas of inverse matrix and of matrix multiplication, or “compounding” as Cayley called it [Richard Feldmann] Dr. Sarah i-clickers in 1.8, 1.9, 2.7 1 0 3. Which of the following are true about the matrix A = k 1 a) determinant of A is 1 b) A is a vertical shear matrix c) When we multiply AB2×n then we have applied 0 r2 = kr1 + r2 to B, because A is the elementary matrix representing that row operation d) more than one of the above e) all of the above Google Scholar search of elementary matrix Dr. Sarah i-clickers in 1.8, 1.9, 2.7 4. By hand, use Laplace expansion as directed 25 2 0 0 −23 60 1 4 3 2 7 6 7 60 0 2 6 3 7 6 7 40 0 3 4 1 5 0 0 0 0 2 Step 1: First expand down the first column to take advantage of the 0s.
    [Show full text]
  • Memory, Penrose Limits and the Geometry of Gravitational
    Published for SISSA by Springer Received: November 26, 2018 Accepted: December 12, 2018 Published: December 21, 2018 Memory, Penrose limits and the geometry of JHEP12(2018)133 gravitational shockwaves and gyratons Graham M. Shore Department of Physics, College of Science, Swansea University, Swansea, SA2 8PP, U.K. E-mail: [email protected] Abstract: The geometric description of gravitational memory for strong gravitational waves is developed, with particular focus on shockwaves and their spinning analogues, gyratons. Memory, which may be of position or velocity-encoded type, characterises the residual separation of neighbouring `detector' geodesics following the passage of a gravi- tational wave burst, and retains information on the nature of the wave source. Here, it is shown how memory is encoded in the Penrose limit of the original gravitational wave spacetime and a new `timelike Penrose limit' is introduced to complement the original plane wave limit appropriate to null congruences. A detailed analysis of memory is presented for timelike and null geodesic congruences in impulsive and extended gravitational shockwaves of Aichelburg-Sexl type, and for gyratons. Potential applications to gravitational wave astronomy and to quantum gravity, especially infra-red structure and ultra-high energy scattering, are briefly mentioned. Keywords: Classical Theories of Gravity, Models of Quantum Gravity ArXiv ePrint: 1811.08827 Open Access, c The Authors. https://doi.org/10.1007/JHEP12(2018)133 Article funded by SCOAP3. Contents 1 Introduction2
    [Show full text]
  • MTH 211 Notes: Matrix Factorizations
    MTH 211 Notes: Matrix Factorizations 1 Introduction When you have things that can be multiplied, it is often useful to think about ways that they can be factored into simpler parts. You've definitely seen stuff like this before! • Any integer n ≥ 2 can be factored into a product of prime numbers. • Factorization of polynomials can be useful in solving polynomial equations. We can multiply matrices, so if we are given a matrix A, we could ask whether it is possible to factor A into simpler parts. Of course, this is question is vague | what do we mean by \simpler parts"? Well, as we'll see later, this ambiguity is good. Different types of \simpler parts" will lead to different ways of factoring matrices, useful in different situations. As we go through the semester, we'll learn about a few different ways to factor matrices. In these notes, we'll learn about a way to factor matrices that is useful in the context that we've been studying, that of solving matrix equations A~x = ~b. In fact, there's a sense in which we've already been doing this factorization without knowing it! 2 Elementary matrices Let's start by introducing three types of matrices that might be considered \simple". The simplest matrix is an identity matrix, but that's too simple. The elementary matrices are, in a sense, minimally more complex than identity matrices; they are matrices that you can get by performing a single row operation on an identity matrix. Because there are three kinds of row operations, there are three kinds of elementary matrices: 1.
    [Show full text]
  • Using Works of Visual Art to Teach Matrix Transformations
    Using Works of Visual Art to Teach Matrix Transformations James Luke Akridge*, Rachel Bowman*, Peter Hamburger, Bruce Kessler Department of Mathematics Western Kentucky University 1906 College Heights Blvd. Bowling Green, KY 42101 E-mail: [email protected], [email protected], [email protected], [email protected] * Undergraduate students. Abstract 2 The authors present a modern technique for teaching matrix transformations on R that incorporates works of visual art and computer programming. Two of the authors were undergraduate students in Dr. Hamburger’s linear algebra class, where this technique was implemented as a special project for the students. The two students generated the im- ages seen in this paper, and the movies that can be found on the accompanying webpage www.wku.edu/˜bruce.kessler/. 1 Introduction As we struggle to increase the number of students succeeding in the science, technology, engineering, and mathematics disciplines, we must keep two things in mind. • We must find ways to motivate a larger audience as to the importance and relevance of these disciplines. • We can not be tied to the old ways of teaching these disciplines to interested students if we intend to keep them interested. As an example of how we can improve the way that we present topics, consider the way that matrix multiplication is typically presented. Matrix multiplication has a number of applications that can attract students, but as we move to a more abstract understanding, we sometimes lose the student’s interest. In general, multiplying an n-vector by a m × n-matrix (that is, a matrix with m rows and n columns) generates n m an m-vector, so it can be interpreted as a transformation from R to R .
    [Show full text]