Comparing Econometric Analyses with Machine Learning Approaches: a Study on Singapore Private Property Market
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

NSS Bird Group Report-Oct 2015
NSS Bird Group Report-Oct 2015 October normally marks the peak passerine migration period for Singapore. Unfortunately it was also the peak time for peatland forest fires in Indonesia resulting in prolonged haze in the region. This is not a rant about our own inconvenience, but before we proceed further, spare a thought for the lost habitat for these migrants that have flown thousands of kilometres to find their wintering ground destroyed. The globally threatened Brown-chested Jungle Flycatcher at Bidadari on 3 October The list of migrants that came to our shore this month is a long one. Among the notable ones are the ever popular Black-backed Kingfisher that landed at Bidadari on 6 October. Bidadari, which is widely considered as the best place in Singapore to see migrant forest birds also played host to numerous Brown-chested Jungle Flycatchers. This globally threatened species made its first appearance on 3 October and a few seemed to have made it their wintering ground. The Siberian Blue Robin, another attractive species that occupy the same bushes and ground as the jungle flycatchers also made its first appearance on 5 October. 1 Ferruginous Flycatcher at Bidadari Other notable sightings at Bidadari include the Asian Paradise Flyacatchers that made their first appearance on 2 October, the attractive Ferruginous Flycatcher on 28 October. The short range migrant from Malaysia, the Malaysian Hawk-Cuckoo made an appearance at Bidadari on 15 October. It’s cousin the similar looking Hodgson’s Hawk-Cuckoo came from further north and consequently made its first appearance on 18 October. -

Routemap SCSM 2018, 9 DECEMBER 2018
KPE EXIT TO KPE NICOLL HIGHWAY CLOSED NICOLL HIGHWAY (1.00AM TO 7.30AM) Geylang Rd Sims Ave (TO CITY USE SIMS AVE EXIT) Guillemard Rd FROM 1.00AM TO 7.30AM Guillemard Rd Geylang Rd Sims Way Way CBD (1.00AM TO 10.30AM) Kallang Rd Kallang Airport Mountbatten Rd Nicoll Highway Kallang Rd Old Airport Rd Stadium Dr WEST COAST (12.00AM TO 12.00PM) Crawford St KPE M Stadium Blvd o North Bridge Rd u n tb a t Merdeka Bridge te Victoria St n Mountbatten Rd R d North Bridge Rd Jln Sultan EAST COAST (1.00AM TO 12.00PM) Ophir Rd Beach Rd National Stadium Marina Parade Rd Java Rd Nicoll Highway P Mountbatten Rd Mountbatten Rd ECP Amber Rd MARINA CENTRE (12.00AM TO 2.00PM) Rochor Rd Republic Ave Fort Rd EAST COAST PARK Victoria St P CARPARK C1 East Coast Park Service Rd Beach Rd Ophir Rd North Bridge Rd Nicoll Highway Meyer Rd East Coast Park Service Rd SUNDAY, 09 DECEMBER 2018 Tanjung Rhu View Tanjung Rhu Rd Killney Rd Meyer Rd Tanjung Rhu Rd Fort Rd Rochor Rd R Rhu Cross Middle Rd e p ECP River Valley Rd Victoria St u b River Valley Rd l P i c B l Tanjung Rhu Flyover (Toll Rd) ECP (Toll Road) v P ECP d East Coast Park Service Rd Bras Basah Rd East Coast Park Service Rd Rafes Hotel Beach Rd ECP Ophir Rd (E t CP Airpor Chijmes ) T hangi owards C TRAFFIC FACILITATION TO South Beach Tower City MARINA BAY GOLF COURSE Stamford Rd ards River Valley Rd River Valley Cl ow ) T Suntec City P Temasek Ave Temasek C (E Temasek Blvd Hill St Raffles Blvd Millenia Walk Marina Bay Golf Course Alexandra Rd AYE (Toll Road) P St. -

Marina-Bay-Residences-Brochure.Pdf
CONTENTS: • Fact Sheet • Location Map • Reasons to Buy • Future Marina Bay Developments • Floor Plans – Typical Apartments • Floor Plans – Penthouses • Payment Schemes & Payment Schedules • Competitors’ Comparison Table • Specifications • Singapore Property Investment Guide (For Local and Foreign Purchasers) For Internal Circulation Only 20 November 2006 MARINA BAY RESIDENCES - FACT SHEET 1 Developer : BFC Development Pte Ltd (A Joint Venture of Cheung Kong (Holdings), Hongkong Land and Keppel Land) 2 Location : Marina Bay 3 Offical Address : 2 Marina Way (To be confirmed) 4 Project Description : 1 Block of 55 Storey residential condominium with facilities 5 Site Area : 5253.6 sm 6 Nearby Amenities : Walking distance to CBD - Raffles Place, Gardens by The Bay, Singapore Flyer, Bayfront Bridge, Marina Barrage, Marina Bay Sands Integrated Resort, Business Financial Centre 7 Tenure : 99 years (wef 14 July 2005) 8 Plot Ratio : 10.469 9 No. of Units : Type Description No. of Units Approx. Floor Area (sm)/ (sf) A 1 bedroom 126 66 - 70 (sm)/ 710 - 753 (sf) B 2 bedroom 174 91 - 114 (sm)/ 980 - 1227 (sf) C 3 bedroom 80 151 - 185 (sm)/ 1625 - 1991 (sf) D 4 bedroom 38 220 - 221 (sm)/ 2368 - 2379 (sf) Duplex Penthouses with E 4 335 - 412 (sm)/ 3606 - 4435 (sf) roof terraces Single Level P 5 416 - 434 (sm)/ 4478 - 4672 (sf) Penthouses Super Penthouse with P roof terraces & private 1 1023 (sm)/ 11011 (sf) pool Total Units: 428 units 10 : Finished Floor to Ceiling Height Description Typical Apartment Penthouses Duplexes Living 3.0m 3.0 - 3.5m 3.0 - 3.5m Dining 3.0m 3.0 - 3.5m 3.0 - 3.5m Kitchen 2.40m 2.4 - 2.7m 2.7 - 3.0m Bedrooms 2.7m - 3.0m 2.7m - 3.2m 3.0m - 4.2m Bathrooms 2.4m 2.4 - 3.0m 2.7 - 3.7m 11 Total Carpark Lots : 343 lots 12 Estimated Maintenance Charges : No. -

An Inspired Vision
AN INSPIRED VISION Be part of a diverse group of individuals in this up-and-coming LOCALE, where opportunity awaits. Enjoy the commute between this trendsetting neighbourhood and the city with its network of enhanced CONNECTIVITY. Create your own SPACE where definitive style meets comfort in a home you can call your own. Bijou. A Far East SOHO development. DISCOVER THE BIJOU APPROACH TO LIFE Shot on location LIFELONG Freehold at Pasir Panjang INTEGRATED With retail and F&B at ground floor and basement LIMITED Just 120 units in this low-rise 5-storey development CONNECTED Directly opposite Pasir Panjang MRT Station and minutes’ drive to Mapletree Business City, Sentosa and CBD DISCOVER THE POTENTIAL OF WHAT’S TO COME Bijou is located at the fringe of the future Greater Southern Waterfront, which extends from Pasir Panjang to Marina East and is set to be developed in 5-10 years' time. Under the URA Draft Master Plan 2019, the area is envisaged to be a gateway to live, work and play with 1,000 ha of land for future development. Bijou is set to benefit from the transformation of this major gateway and is well-connected to public transport nodes and amenities. Shot on location The Straits Times | Friday, March 8, 2019 sure that every town is well-devel- oped, with good amenities and con- Gateways and long-term plans for a green Singapore venient access to transport nodes and job centres near home, he said. Plans to While these efforts do not “auto- matically equalise property values”, the Government can “temper some of the excesses in the market”. -

Reference Projects for ROCKINSUL in Singapore
Reference Projects for ROCKINSUL in Singapore 1C Sakra Ave ( Evonik @ Jurong Island ) Apple HQ At Ang Mo Kio Hub - GALILEO Project Asia Square Tower @ Marina Bay ASME Technology Auditorium @ SP (Gate 8) Beatty Secondary School @ No.1 Toa Payoh North Bendemeer Primary School Boon Lay Community Centre Bukit Panjang N5C13 Canberra & Yio Chu Kang Primary School Centra Place @ 1 Hougang St.1 Changi Prison Complex Chinatown Point Dazhong Primary School @ Bukit Batok DBS Showflat Downtown Line Project East Spring Primary School@ Tampines GLYNOEBROURNE Hamilton Scotts @ Orchard Road ITE Central Ang Mo Kio Lengkok Mariam 2 Light Industrial @ Lavendar St Marina Bay Financial Centre Tower 3 (MBFC Tower 3) Miri Malaysia Project MOM Building @ Bendemeer Road Mural Camp Upgrading Nanyang Poly Technic Nissim Hill Condo No.151 bencoleen st ( NAFA CAMPUS 3 4th STOREY ) NTU Hall of Residence NUS Block MD6 www.rockwoolindia.com Reference Projects for ROCKINSUL in Singapore One North @ 3 Fusiono Polis Link Pacnet Project , Paya Lebar River Safari Mandai Zoo Roche - Tuas Bay Link SAF Armour Centre Samsung GMR Energy Project - Jurong Island Scanning Station @ Brani Terminal Ave Scare Hotel @ Chin Swee Road Schenker Schenker Building @ Changi School at Woodlands Crescent Seacare Hotel @ Chin Swee Road Seletar Hanger Project Sengkang Primary School Sg Poly ( Blk ) 1 @ Dover Road Singapore American School Singapore Polytechnic Block 1 SIP Denki Project Space @ Kovan SUTD Campus @ Changi Tampines Substation Tan Tock Seng Hospital Tannery @ Choa Chu Kang Road Temp Holding Building @ NTU The Heeren The Signature Building @ Changi Business Park TUAS DEPOT C1685 Tuas Mega Shipyard Tuas Naval Base Tuas South Boulevard Mega Yard Store Tuas West C1685 UPS Hotel @ Upper Pickering Street (Park Royal Hotel) Westgate @ Jurong East Yio Chu Kang Primary School Yishun Polyclinic Yishun Ring Road (Lup G98) Blk 326 www.rockwoolindia.com Reference Projects for ROCKINSUL in Singapore 1 Marina Boulevard (NTUC Centre) 211 Temp Sports Facility @ Sin Ming ave 25 International Business Park. -

3.SG Unhabitat Ilugp Integrated Master Planning and Development
INTEGRATED MASTER PLANNING & DEVELOPMENT SG UNHabitat iLUGP Speaker Michael Koh Fellow, Centre for Liveable Cities Singapore Liveability Framework Outcomes of Liveability 1. High Quality of Life 2. Competitive Economy 3. Sustainable Environment Singapore Liveability Framework Principles of Integrated Master Planning and Development 1. Think long term 2. “Fight productively” 3. Build in flexibility 4. Execute effectively 5. Innovate systematically Outline Principles of Integrated Master Planning and Development 01 Concept Plan 02 Master Plan 03 Integrated Transport Planning 04 Urban Design Controls 05 Conservation Concept Plan 01 Concept Plan 02 Master Plan 03 Integrated Transport Planning 04 Urban Design Controls 05 Conservation Planning and Development Framework CONCEPT PLAN Maps out strategic vision over the next 40-50 years MASTER PLAN Guides development over the next 10-15 years LAND SALES & DEVELOPMENT DEVELOPMENT COORDINATION CONTROL Concept Plan Review Process Identify long term land requirements (including Phase 1 planning assumptions, standards and projections) and key planning policies for all land use types Formulate and design structure plans and Phase 2 development strategies Phase 3 Traffic modelling, plan evaluation and refinement Phase 4 Monitoring and update of concept plan Concept Planning Framework & Strategic Planning Components POPULATION PROJECTIONS 8 CRITICAL AREAS Integrator: URA INDUSTRY [MTI/JTC] COMMERCE DEVELOPMENT LAND SUPPLY [EDB] INFRASTRUCTURE [PUB] CONSTRAINTS ENVIRONMENT [NEA] RECREATION [NPARKS] HOUSING -

(Section 9 (2)) BOUNDARIES of ALTERED POLLING DISTRICTS
FRIDAY, SEPTEMBER 24, 2004 1 First published in the Government Gazette, Electronic Edition, on 24th September 2004 at 11.00 am. No. 2349 — PARLIAMENTARY ELECTIONS ACT (CHAPTER 218) (Section 9 (2)) BOUNDARIES OF ALTERED POLLING DISTRICTS Take notice that the subdivision of every electoral division into polling districts has been altered and the new polling districts and distinguishing letters thereof are as follows: ELECTORAL DIVISION OF ALJUNIED Name and POLLING DISTRICT Distinguishing Distinguishing Letters of Letters and Boundaries Electoral Division Numbers ALJUNIED AJ01 The area bounded by Hougang Avenue AJ 10, Sungei Pinang, Sungei Serangoon, Tampines Expressway, Tampines Road, Sungei Serangoon, imaginary boundary across the former bed of Sungei Serangoon (common boundary of AJ01 and HOUGANG), Upper Serangoon Road, Hougang Central, Hougang Avenue 10, imaginary boundary between Block Nos. 460, 408, 407, 467, 468 and Block Nos. 410, 409, 404, 406, 405, 402, 401 (common boundary of AJ01 and AJ02) and Hougang Avenue 8. AJ02 The area bounded by Hougang Avenue 10, Hougang Avenue 8 and imaginary boundary as described in AJ01 (common boundary of AJ02 and AJ01). AJ03 The area bounded by Hougang Avenue 8, Hougang Avenue 10 and Hougang Avenue 6. AJ04 The area bounded by Hougang Avenue 8, Hougang Avenue 6, Hougang Avenue 10 and imaginary boundary between Block Nos. 522, 525, 526, 527, 530, 531 and Block Nos. 521, 523, 524, 520, Montfort Junior School (common boundary of AJ04 and AJ05). 2 REPUBLIC OF SINGAPORE GOVERNMENT GAZETTE ELECTORAL DIVISION OF ALJUNIED — continued Name and POLLING DISTRICT Distinguishing Distinguishing Letters of Letters and Boundaries Electoral Division Numbers ALJUNIED AJ05 The area bounded by Hougang Avenue AJ 8, imaginary boundary as described in AJ04 (common boundary of AJ05 and AJ04), Hougang Avenue 10, Hougang Avenue 4 and imaginary boundary between Block Nos. -

Annual Report 2018/2019
ANNUAL REPORT 2018/2019 SINGAPORE’S NATIONAL WATER AGENCY 1 Contents Mission and Vision .......................................................................................................................... 4 Organisation Structure ................................................................................................................... 6 Board of Directors ........................................................................................................................... 7 Key Highlights and Achievements ........................................................... 8 Strengthening Water Supply ....................................................................................................... 10 Reclaiming Used Water ................................................................................................................ 10 Taming Stormwater ...................................................................................................................... 11 PUB, Singapore’s National Water Agency Annual Report for the year ended 31 March 2019 Managing Water Demand and Costs........................................................................................... 12 Building Capabilities ..................................................................................................................... 14 In the opinion of the directors, Encouraging Community Ownership .......................................................................................... 20 the annual report of the PUB, Singapore’s -

Mark Goh's Speech
SINGAPORESINGAPORE’’’’SS WATERFRONT REJUVENATION EFFORTS A Presentation by Mr Mark Goh, Head (Marina Bay Development Agency), Urban Redevelopment Authority, Singapore delivered to the Harbour Business Forum Luncheon in Hong Kong on 28 Mar 2007 IntroIntroductionduction 1 Much like Hong Kong, Singapore as an island city has been blessed with a long coastline and waterbodies right in the heart of the city centre. Within and near the City Centre, we have the Singapore River, Kallang Basin and Marina Bay. Today, I would like to share our experience of developing these waterfront areas and the strategies we took to help us transform these urban waterfront areas. Singapore River 2 Let me start with the Singapore River. The 3km long Singapore River is located in the City Centre. The sheltered banks of the river made it an excellent place for trading and warehousing activities since Singapore’s colonial days. Merchants were quick to build offices, godowns and jetties to facilitate these activities along the riverbanks. 3 By the 1860s, three quarters of all shipping businesses in Singapore was done here. By the 1970s, as business proliferated, so did the pollution. Both the river banks and water became polluted by the myriad activities and squatters along the river. In fact, the river was like an open sewer. 4 The task to clean up Singapore River was an enormous one, and involved many government agencies. To start off, all the boats were moved out to Pasir Panjang as container shipping had replaced this earlier mode of transporting goods from the ships to the godowns. Tonnes of garbage were dredged from the river. -
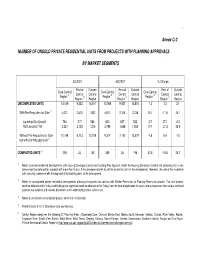
Annex C-2 NUMBER of UNSOLD PRIVATE RESIDENTIAL UNITS
1 Annex C-2 NUMBER OF UNSOLD PRIVATE RESIDENTIAL UNITS FROM PROJECTS WITH PLANNING APPROVALS BY MARKET SEGMENTS 3Q/2007 4Q/2007 % Change Rest of Outside Rest of Outside Rest of Outside Core Central Core Central Core Central Central Central Central Central Central Central Region 4/ Region 4/ Region 4/ Region 5/ Region Region 5/ Region Region 5/ Region UNCOMPLETED UNITS 14,169 9,333 14,511 13,988 9,457 14,815 -1.3 1.3 2.1 With Pre-Requisites for Sale 1/ 4,021 2,620 1,802 4,611 2,315 2,236 14.7 -11.6 24.1 Launched But Unsold 794 517 586 823 657 583 3.7 27.1 -0.5 Not Launched Yet 3,227 2,103 1,216 3,788 1,658 1,653 17.4 -21.2 35.9 Without Pre-Requisites for Sale 10,148 6,713 12,709 9,377 7,142 12,579 -7.6 6.4 -1.0 but with planning approvals 2/ COMPLETED UNITS 3/ 293 43 150 389 35 190 32.8 -18.6 26.7 1/ Refers to private residential developments with Housing Developer Licence and Building Plan Approval. Under the Housing Developer (Control and Licensing) Act, a sale licence must be obtained for a project with more than 4 units, if the developer intends to sell the residential units in the development. However, the sale of the residential units can only commence with the approval of the building plans of the development. 2/ Refers to uncompleted private residential developments without pre-requisites for sale but with Written Permission or Planning Permission granted. -

Land Use Planning in Singapore
Examples from Singapore Hwang Yu-Ning URBAN OUR MISSION REDEVELOPMENT AUTHORITY To make Singapore a great city to live, work and play in 1 Outline . Context of planning in Singapore . Public Housing programme . one north . [if there’s time] Singapore River, Tanjong Rhu, Marina Bay, Southern Ridges . Lee Kuan Yew World City Prize 2 South Korea China India Vietnam Philippines 2 SINGAPORE 710 km Indonesia 5 million population Singapore Has Limited Land • One of the most densely populated cities in the world • Smaller than other cities Land Area: 710 km2 • No hinterland, unlike other cities Population: 5 mil City centre 4 Competing Land Needs Housing Port Airport Commerce Parks Industry Water treatment & storage5 Constraints on our Developments Port Airport Power Station Water treatment plant Industry 6 Safeguard Sufficient Land for Good Quality of Life 7 Sustainable Development in Singapore Economic growth Culture and Heritage Cohesive Community Pro-Business Environmental Environment Responsibility Key Objective Balancing economic growth and development to achieve Sustained Economic Growth – Resource Efficiency and Security & High Quality Living Environment – Clean, Green, Healthy, Pleasant Environment Overview Resource Pollution Transport Greening/ Management Control Management Biodiversity Land Use Planning Resource Management: Water ENSURING A DIVERSIFIED, ADEQUATE AND SUSTAINABLE SUPPLY OF WATER Four National Taps CLOSING THE WATER LOOP From sourcing, collection, purification and supply of drinking water, to treatment of used water and turning it into NEWater, drainage of storm water Rain Sea NEWater Direct Non- Potable Use The Deep Tunnel Sewerage System a wastewater conveyance, treatment and disposal system will replace the existing sewage treatment works and 139 pumping stations located at various parts of Singapore Deep Tunnel Sewerage System CHANGI WRP Resource Management: Waste Waste Management System All waste: 54% recycled, 43% incinerated, 3% landfill Semakau – Not just an offshore landfill. -

Ours to Run. It's
M ou nt Nicoll Hwy ba tte Stadium Dr n Rd F1 Pit Building Crawford St Stadium Blvd Nicoll Highway National Stadium Merdeka Bridge SPORTS HUB South Beach Beach Rd 2 1 KM (Former NCO Club) AS Nicoll Hwy ve A Hill St lic ub Mountbatten Rd ep R Stadium Cr Marine Parade Rd Ophir Rd 40 ECP Beach Road KM Amber Rd 1KM KPE Rochor Rd North Bridge Rd 21 ECP Service Rd AS 15 e AS v A c Fort Rd i l War Memorial Park Middle Rd b 3KM u Tanjong Rhu View p e R Tanjong Rhu Rd Meyer Rd EAST COAST Marathon Tanjong Rhu Rd B2 CAR PARK Victoria St R ECP h 28 27 Nicoll Hwy KM u KM St. Andrew’s Road C Beach Rd r o 14 s 29 s Tanjong Rhu Flyover KM AS Bras Basah Rd ECP 42.195km Route Suntec City 26KM Raffles Hotel 17 ECP AS StamfordChijmes Rd FOUNTAIN OF WEALTH St. Andrew’s Cathedral 32KM MCE South Beach 41 Suntec Convention Centre KM Rhu Cross d v l B Legend 4KM s 39 e KM l Raffles Blvd f f a R 16 30 AS KM National Gallery War Memorial Park Pan Pacific s MARINA BAY e EAST COAST PARK r GOF COURSE St. Andrew’s Cathedral Millenia Walk a e Marina Mandarin h S n START 25 i M 13 KM e AS v BY THE BAY EAST a A Marina Square m r i s n a e a j l Merlion Park f St Andrew’s Rd National Gallery f GARDENS E n Mandarin Oriental a a R s 2 e AS t The Ritz-Carlton D Parliament Pl B MARINA BAY r Connaught Dr MARINA EAST 42KM Raffles Ave THE PADANG 33KM Marina East Dr Esplanade 31KM Fullerton Hotel FINISH Singapore Flyer THE FLOAT @ MARINA BAY Esplanade Dr One Fullerton Bayfront Ave South Canal Rd Fullerton Hotel Merlion Park ArtScience Museum Sheares Ave 5KM 38 24 Collyer Quay KM