Research 1..9
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Max-Planck-Institut Für Chemische Energiekonversion
MAX-PLANCK-INSTITUT FÜR CHEMISCHE ENERGIEKONVERSION MPI für Chemische Energiekonversion • PF 10 13 65 • D-45413 Mülheim a. d. Ruhr Christin Ernst M.A. Forschungskommunikation [email protected] Tel.: +49-208-306-3681 Fax: +49-208-306-3956 8. August 2019 How Nature splits water and powers the planet An international research team including the Max Planck Institute for Chemical Energy Conversion (MPI CEC) in Germany and The Australian National University (ANU) has published new results on how nature performs biological water splitting, a process that underpins all life on the planet. The results can be valuable for the production of CO2 free ‘solar fuels’. The splitting of two water molecules into oxygen using sunlight is the first step of photosynthesis, a process performed by plants and cyanobacteria. The overall reaction operates much the same way as a roof-top solar panel, harvesting light energy from the sun. But instead of generating electricity, the energy is used to produce chemical compounds like carbohydrates, the food animals and humans consume. It has also created the oxygen rich atmosphere of our planet, and the protective ozone layer, which shields the surface from harmful UV radiation. The study, led by Dr. Nick Cox, a former group leader of MPI CEC in the Department of Prof. Wolfgang Lubitz, now at ANU Research School of Chemistry, focused on the photosynthetic enzyme which performs biological water splitting, Photosystem II. Buried within this large protein complex is a cofactor consisting of four manganese and one calcium metal ions. It is this cofactor that performs the water splitting reaction, binding the two waters in close proximity to allow them to join together to form a single oxygen molecule. -
![[Nife] Hydrogenase: Functional Spectroscopy of the Active Site Maria-Eirini Pandelia, Hideaki Ogata, and Wolfgang Lubitz*[A]](https://docslib.b-cdn.net/cover/3428/nife-hydrogenase-functional-spectroscopy-of-the-active-site-maria-eirini-pandelia-hideaki-ogata-and-wolfgang-lubitz-a-803428.webp)
[Nife] Hydrogenase: Functional Spectroscopy of the Active Site Maria-Eirini Pandelia, Hideaki Ogata, and Wolfgang Lubitz*[A]
DOI: 10.1002/cphc.200900950 Intermediates in the Catalytic Cycle of [NiFe] Hydrogenase: Functional Spectroscopy of the Active Site Maria-Eirini Pandelia, Hideaki Ogata, and Wolfgang Lubitz*[a] The [NiFe] hydrogenase from the anaerobic sulphate reducing monoxide or molecular oxygen and the light-sensitivity of the bacterium Desulfovibrio vulgaris Miyazaki F is an excellent hydrogenase. The methods employed include magnetic reso- model for constructing a mechanism for the function of the nance and vibrational (FTIR) techniques combined with electro- so-called ‘oxygen-sensitive’ hydrogenases. The present review chemistry that deliver information about details of the geo- focuses on spectroscopic investigations of the active site inter- metrical and electronic structure of the intermediates and their mediates playing a role in the activation/deactivation and cata- redox behaviour. Based on these data a mechanistic scheme is lytic cycle of this enzyme as well as in the inhibition by carbon developed. 1. Introduction to [NiFe] Hydrogenases Hydrogen conversion by the enzyme hydrogenase has become a field of intensive research in recent years due to a continu- ously increasing interest into attaining hydrogen-based energy sources.[1–3] Hydrogenases[4] are involved in the metabolic ma- chinery of a wide variety of microorganisms by catalysing the reversible heterolytic splitting of dihydrogen according to the elementary reaction (1):[5] À þ þ À H2 Ð H þ H Ð 2H þ 2e ð1Þ The production and engineering of hydrogenases is pivotal Figure 1. The active site and the iron-sulphur clusters of the [NiFe] hydroge- for the design of biocatalysts that are focused either on biohy- nase from D. -

Joshua Telser Curriculum Vitae
JOSHUA TELSER CURRICULUM VITAE Department of Biological, Physical, and Health Sciences voice: 1 312 341 3687 Roosevelt University fax: 1 312 341 4358 430 S. Michigan Ave. E-mail: [email protected] Chicago, IL 60605-1394 USA Website: http://blogs.roosevelt.edu/jtelser/ EDUCATION: Northwestern University, Evanston, IL; USPHS/NIH Postdoctoral Fellow, September 1984 – September 1986. Postdoctoral advisor: Prof. Brian M. Hoffman. University of Florida, Gainesville, FL; Ph.D. in Inorganic Chemistry, December 1984. University of Illinois, Urbana, IL; graduate student in Inorganic Chemistry, 1980 – 1983. Thesis advisor: Prof. Russell S. Drago (deceased). Cornell University, Ithaca, NY; A.B. in Chemistry (with distinction), May 1980. WORK EXPERIENCE: 9/95 – present: Associate Professor of Chemistry, Roosevelt University, Chicago/Schaumburg, IL; Chemistry Program Coordinator, 1998 – 2000. Assistant Chair, Department of Biological, Chemical and Physical Sciences, 2005 – 2012; 2016 – 2018; Assistant Chair, Department of Biological, Physical, and Health Sciences, 2018 – present. 9/90 – 9/95: Assistant Professor of Chemistry. Taught General Chemistry I and II (CHEM 201, 202), Organic Chemistry Survey (CHEM 210), Inorganic Chemistry (CHEM 341/441), Organometallic Chemistry (CHEM 319/419), Bioinorganic Chemistry (BCHM/CHEM 344/444), and Analytical, Organic, Inorganic, and Physical Chemistry Laboratory courses (CHEM 203, 210, 347, 325), Chemistry Seminar (CHEM 393/493). Research in paramagnetic resonance and magnetic properties of inorganic and biological systems. 9/89 – 9/90: Research Associate, Department of Biochemistry, University of Chicago, Chicago, IL. Research on enzyme catalysis using nitroxide spin-labeled substrates and vanadyl-nucleotide complexes. 4/88 – 9/89: Research Investigator, Contrast Media Department, Squibb Institute for Medical Research, New Brunswick, NJ. -

Substrate Water Binding to the Oxygen-Evolving Complex in Photosystem II
Substrate water binding to the oxygen-evolving complex in photosystem II Håkan Nilsson Department of Chemistry Umeå University Umeå 2014 © Håkan Nilsson, 2014 This work is protected by the Swedish Copyright Legislation (Act 1960:729) ISBN: 978-91-7459-802-5 Cover:Sunset through leaf, Umeå river 2013-09-21 Digital version available at http://umu.diva-portal.org/ Printed by: Print & Media, Umeå University Umeå, Sweden 2014 Till Ylva, Alma & Elvira “Tron kan försätta berg men tvivlet kan sätta tillbaks dem igen” Tage Danielsson Eftertanke, Tankar från roten (1974) Table of Contents Table of Contents i List of papers ii Abstract iii Abbreviations v Introduction 1 The origin of Earth 1 The origin of life and oxygenic photosynthesis 1 Journey into a leaf 2 Light absorbtion and charge separation 5 Electon transfer by redox active cofactors 7 Kok’s S-state model of photosynthetic water oxidation 9 Proteins and oxygen evolution 10 The oxygen evolving complex 11 Tyrosine Z and D 13 Effect of cofactor replacement 13 Substrate water binding 14 Materials and Methods 16 Substrate water exchange 18 18 Determination of H2 O-injection rate 22 Flash-induced oxygen oscillation pattern 24 Oxygen evolution at elevated pressure 24 Results and discussion 26 Are both substrate molecules bound in the S2 state? (Paper I) 27 Is W1 a substrate water? (Paper II) 30 Is Ca a substrate binding site? (Paper III) 31 Possible mechanism of O-O bond formation 33 What is the driving force for the S4 → S0 transition? (Paper IV) 34 The oxygen water isotope exchange (OWIE) (Paper IV) 34 O2 overpressure (Paper IV) 35 Acknowledgements 38 References 40 i List of papers I. -
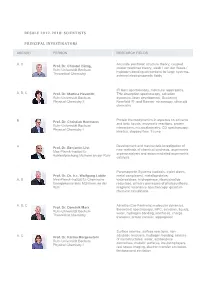
Resolv 2012-2018: Scientists Principal Investigators
RESOLV 2012-2018: SCIENTISTS PRINCIPAL INVESTIGATORS AREA(S) PERSON RESEARCH FIELDS A, C Accurate electronic structure theory, coupled Prof. Dr. Christof Hättig cluster response theory, weak / van der Waals / Ruhr-Universität Bochum hydrogen-bonding interactions for large systems, Theoretical Chemistry external electromagnetic fields IR laser spectroscopy, molecular aggregates, A, B, C Prof. Dr. Martina Havenith THz absorption spectroscopy, solvation Ruhr-Universität Bochum dynamics, laser development, Scattering Physical Chemistry II Nearfield IR- and Raman- microscopy, ultracold chemistry Protein thermodynamics in aqueous co-solvents B Prof. Dr. Christian Herrmann and ionic liquids, enzymatic reactions, protein Ruhr-Universität Bochum interactions, microcalorimetry, CD spectroscopy; Physical Chemistry I kinetics, stopped flow, T-jump Development and mechanistic investigation of A Prof. Dr. Benjamin List new methods of chemical synthesis, asymmetric Max-Planck-Institut für organocatalysis and anion mediated asymmetric Kohlenforschung Mülheim an der Ruhr catalysis Paramagnetic Systems (radicals, triplet states, Prof. Dr. Dr. h.c. Wolfgang Lubitz metal complexes), metalloproteins: A, B Max-Planck-Institut für Chemische wateroxidase, hydrogenase, ribonucleotide Energiekonversion Mühlheim an der reductase; primary processes of photosynthesis; Ruhr magnetic resonance spectroscopy; quantum chemical calculations A, B, C Ab initio (Car-Parrinello) molecular dynamics, Prof. Dr. Dominik Marx theoretical spectroscopy, HPC, solvation, liquids, Ruhr-Universität -

Programme 70Th Lindau Nobel Laureate Meeting 27 June - 2 July 2021
70 Programme 70th Lindau Nobel Laureate Meeting 27 June - 2 July 2021 Sessions Speakers Access Background Scientific sessions, Nobel Laureates, Clear guidance Everything else social functions, young scientists, to all viewing there is to know partner events, invited experts, and participation for a successful networking breaks moderators options meeting 2 Welcome Two months ago, everything was well on course to celebrate And yet: this interdisciplinary our 70th anniversary with you, in Lindau. anniversary meeting will feature But with the safety and health of all our participants being the most rich and versatile programme ever. of paramount importance, we were left with only one choice: It will provide plenty of opportunity to educate, inspire, go online. connect – and to celebrate! Join us. 4 PARTICIPATING LAUREATES 4 PARTICIPATING LAUREATES 5 Henry A. Joachim Donna George P. Hartmut Michael M. Adam Hiroshi Kissinger Frank Strickland Smith Michel Rosbash Riess Amano Jeffrey A. Peter Richard R. James P. Randy W. Brian K. Barry C. Dean Agre Schrock Allison Schekman Kobilka Barish John L. Harvey J. Robert H. J. Michael Martin J. Hall Alter Grubbs Kosterlitz Evans F. Duncan David J. Ben L. Edmond H. Carlo Brian P. Kailash Elizabeth Haldane Gross Feringa Fischer Rubbia Schmidt Satyarthi Blackburn Robert B. Reinhard Aaron Walter Barry J. Harald Takaaki Laughlin Genzel Ciechanover Gilbert Marshall zur Hausen Kajita Christiane Serge Steven Françoise Didier Martin Nüsslein- Haroche Chu Barré-Sinoussi Queloz Chalfie Volhard Anthony J. Gregg L. Robert J. Saul Klaus William G. Leggett Semenza Lefkowitz Perlmutter von Klitzing Kaelin Jr. Stefan W. Thomas C. Emmanuelle Kurt Ada Konstantin S. -

“Metalloproteins at the Crossroads of Design & Nature”
Virtual Symposium “Metalloproteins at the crossroads of design & nature” 27 January 2021 Keynote Lecture Prof. Hannah Shafaat Ohio State University Emergent Complexity: Reconstructing primordial energy conversion processes in model metalloproteins Abstract: Nature has evolved diverse systems to carry out energy conversion reactions. Metalloenzymes such as hydrogenase, carbon monoxide dehydrogenase, acetyl coenzyme A synthase, and methyl coenzyme M reductase use earth- abundant transition metals such as nickel and iron to generate and oxidize small-molecule fuels such as hydrogen, carbon monoxide, acetate, thioesters, and methane. These reactions are highly valuable to understand and harness in the context of the impending global energy and climate crisis. However, the native enzymes require complex multimetallic cofactors, are costly to isolate, highly sensitive to external conditions, and generally poorly suited for large- scale application. We are applying metalloprotein engineering approaches in order to better understand the mechanisms of the native enzymes and develop robust functional models with potential for implementation in anthropogenic energy conversion. Robust metalloprotein scaffolds such as rubredoxin, ferredoxin, and azurin and have been converted into model systems that mimic the structure and function of complex nickel metalloenzymes. By introducing non-native metals and redesigning the primary and secondary coordination spheres, we have installed novel activity into these simple electron transfer proteins, including -

PUBLIKATIONSLISTE W. Lubitz, K.P. Dinse, K. Möbius and R. Biehl
PUBLIKATIONSLISTE Wolfgang Lubitz 1. W. Lubitz, K.P. Dinse, K. Möbius and R. Biehl Fluorine and Proton ENDOR of Aromatic Radicals in Solution Chem. Phys. 8, 371-383 (1975) 2. R. Biehl, W. Lubitz, K. Möbius and M. Plato Observation of Deuterium Quadrupole Splittings of Aromatic Free Radicals in Liquid Crystals by ENDOR and TRIPLE Resonance J. Chem. Phys. 66, 2074-2078 (1977) 3. R. Biehl, K. Hinrichs, H. Kurreck, W. Lubitz, U. Mennenga and K. Roth ESR, NMR and ENDOR Studies of Partially Deuterated Phenyl Substituted Anthracenes. π-σ Delocalization J. Am. Chem. Soc. 99, 4278-4286 (1977) 4. W. Lubitz, R. Biehl and K. Möbius Sodium and Proton ENDOR and TRIPLE-Resonance Experiments on Biphenyl and Fluorenone Ion Pairs in Solution J. Magn. Reson. 27, 411-417 (1977) 5. R. Biehl, Ch. Hass, H. Kurreck, W. Lubitz and S. Oestreich ESR and ENDOR Studies of Partially Deuterated and Chlorinated Phenalenyls Tetrahedron 34, 419-424 (1978) 6. B. Kirste, H. Kurreck, W. Lubitz and K. Schubert 13C ENDOR Studies of Organic Doublet and Triplet State Molecules J. Am. Chem. Soc. 100, 2292-2299 (1978) 7. H.-J. Fey, W. Lubitz, H. Zimmermann, M. Plato, K. Möbius and R. Biehl 13C- and Proton-ENDOR Studies of 13C-labelled Organic Radicals Z. Naturforsch. 33a, 514-522 (1978) 8. W. Lubitz, W. Broser, B. Kirste, H. Kurreck and K. Schubert 13C- and 1H-ENDOR Studies of a Phenoxyl Type Radical Z. Naturforsch. 33a, 1072-1076 (1978) 9. H. J. Fey, H. Kurreck and W. Lubitz ENDOR Studies of [6] Helicene Anion Radical Tetrahedron 35, 905-907 (1979) - 2 - 10. -

Press Release
Press Release Mülheim, Saclay 15.08.2014 Solar fuels as generated by nature Thanks to new insights into the details of photosynthetic water splitting, the prospects for the development of clean fuels based on water and sunlight are improving Summary: Society’s energy supply problems could be solved in the future using a model adopted from nature. During photosynthesis, plants, algae and some species of bacteria produce sugars and other energy-rich substances (i.e. fuels) using solar energy. A team headed by researchers from the Max Planck Institute for Chemical Energy Conversion in Mülheim an der Ruhr is currently developing experimental methods to ascertain how this process occur in nature. The scientists are investigating a particularly important cofactor involved in photosysthesis, a manganese-calcium complex, which uses solar energy to split water into molecular oxygen. They have determined the exact structure of this complex at a crucial stage in this chemical reaction. This has led to a detailed suggestion as to how molecular oxygen, O2, is formed at this metal complex. Through these new insights into photosynthesis, the scientists have provided a blueprint for synthetic systems that could store sunlight energy in chemical energy carriers. For over three billion years, nature has been using sunlight as its primary energy source in photosynthesis. In the course of this process, plants, algae and cyanobacteria (blue-green algae) use sunlight to split water and produce energy- rich chemical compounds from carbon dioxide (CO2). The end product is carbohydrates which, in nature, act as solar fuels in the living cell. Although the basic reactions involved in photosynthesis has been known for a long time, researchers from the Max Planck Institute for Chemical Energy Conversion in Mülheim an der Ruhr and the Commissariat à l'Énergie Atomique (CEA) in Saclay, France, have now succeeded in explaining The structure of the manganese cluster as important details of the light-induced water it is found in nature and prior to O-O bond splitting process. -

Light-Induced Water Splitting and Hydrogen Production in Nature
Light-Induced Water Splitting and Hydrogen Production in Nature: Basis for the Design of Bioinspired Molecular Catalysts Wolfgang Lubitz Max-Planck-Institut für Chemische Energiekonversion, Stiftstr. 34-36, 45470 Mülheim an der Ruhr, [email protected] Storage of the sun’s energy in „solar fuels“ like molecular hydrogen or related molecules using water as a basic material is a research topic of great importance for our society. A promising start point for the development of synthetic sun light-driven water splitting catalyst, is to use Nature’s approach for inspiration that is realized by the tetranuclear manganese cluster in photosystem (PS) II of oxygenic photosynthesis.1 Many bacteria and green algae also contain enzymes that enable hydrogen evolution from excess protons, the hydrogenases.2 In recent years high resolution X-ray crystallographic structures of PS II4 and different hydrogenases2,3 have been obtained and additional spectroscopic and electrochemical experiments have very significantly increased our knowledge about the structure and function of the native enzymes leading to a mechanistic understanding of the underlying processes. This knowledge will help to advance the field of artificial photosynthesis, aiming at synthesizing new catalyst for large scale water splitting, hydrogen production or energy storage in other chemical compounds, processes that are of key importance for a sustainable energy future. In this lecture the native metalloenzymes wateroxidase and hydrogenase are presented and their working mechanisms are discussed. Prospects of native biological and artificial chemical systems to solve the energy problems will also be addressed. References (1) Cox, N.; Pantazis, D. A.; Neese, F.; Lubitz, W. -

Annual Report 2017
67th Lindau Nobel Laureate Meeting 6th Lindau Meeting on Economic Sciences Annual Report 2017 The Lindau Nobel Laureate Meetings Contents »67 th Lindau Nobel Laureate Meeting (Chemistry) »6th Lindau Meeting on Economic Sciences Over the last 67 years, more than 450 Nobel Laureates have come 67th Lindau Nobel Laureate Meeting (Chemistry) Science as an Insurance Policy Against the Risks of Climate Change 10 The Interdependence of Research and Policymaking 82 to Lindau to meet the next generation of leading scientists. 25–30 June 2017 Keynote by Nobel Laureate Steven Chu Keynote by ECB President Mario Draghi The laureates shape the scientific programme with their topical #LiNo17 preferences. In various session types, they teach and discuss Opening Ceremony 14 Opening Ceremony 86 scientific and societal issues and provide invaluable feedback Scientific Chairpersons to the participating young scientists. – Astrid Gräslund, Professor of Biophysics, Department of New Friends Across Borders 16 An Inspiring Hothouse of Intergenerational 88 Biochemistry and Biophysics, Stockholm University, Sweden By Scientific Chairpersons Astrid Gräslund and Wolfgang Lubitz and Cross-Cultural Exchange Outstanding scientists and economists up to the age of 35 are – Wolfgang Lubitz, Director, Max Planck Institute By Scientific Chairpersons Torsten Persson and Klaus Schmidt invited to take part in the Lindau Meetings. The participants for Chemical Energy Conversion, Germany Nobel Laureates 18 include undergraduates, PhD students as well as post-doctoral Laureates 90 researchers. In order to participate in a meeting, they have to Nominating Institutions 22 pass a multi-step application and selection process. 6th Lindau Meeting on Economic Sciences Nominating Institutions 93 22–26 August 2017 Young Scientists 23 #LiNoEcon Young Economists 103 Scientific Chairpersons SCIENTIFIC PROGRAMME – Martin F. -

New X-Ray Spectroscopy Explores Hydrogen-Generating Catalyst
New X-ray spectroscopy explores hydrogen- generating catalyst 22 November 2017, by Andy Fell in the future hydrogen economy, either by a direct use or by a synthetic complex which has a similar reaction center," said Professor Stephen P. Cramer in the UC Davis Department of Chemistry and coauthor on the paper along with graduate students Cindy C. Pham (co-first author) and Nakul Mishra and project scientist Hongxin Wang in the same department. The researchers used a technique called nuclear resonant vibrational spectroscopy (NRVS) to follow the vibrational structures and analysis activity at the iron atoms in the enzyme. NRVS requires special equipment, and is currently only available at four sites in the world: the SPring-8 synchrotron in Using a newly developed technique and one of the Hyogo, Japan, where this study was carried out; world's most advanced X-ray sources, researchers from the Advanced Photon Source at Argonne National Japan, Germany and the US are studying enzymes that Laboratory, Illinois; the European Synchrotron can produce hydrogen gas. Understanding these Radiation Facility in Grenoble, France; and Petra-III reactions could be important in developing a clean-fuel in Hamburg, Germany. economy powered by hydrogen. Credit: Cramer Lab, UC Davis Using a newly developed technique, researchers from Japan, Germany and the U.S. have identified a key step in production of hydrogen gas by a bacterial enzyme. Understanding these reactions could be important in developing a clean-fuel economy powered by hydrogen. The team studied hydrogenases - enzymes that catalyze production of hydrogen from two widely distributed organisms: Chlamydomonas reinhardtii, a single-cell algae and Desulfovibrio desulfuricans, a bacterium.