DOCSLIB.ORG

Proceedings of the Spring Meeting of the Society of Naval

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Proceedings of the Spring Meeting of the Society of Naval I Cr%-ot-2,%4-o © ETDE-/of- m?- - ?1731593 - cmiem im-mm-mm- mm) i-i mmt>o©^nus-ita gg%-sm mi-f# #...... (T) .................................................................................................jus 3s#-sm ...... (n/ 1- 3 JS7X^ HtjJfJKKS-o* < Sj&ffcc i % .....................................................................................................j&# £$•■ 21 1- 4 Numerical Study on the Aerodynamic Characteristics of a Three-Dimensional Power-Augmented Ram Wing in Ground Effect .................................. VEB fitfr- 31 l- 5 bKimowmi's * 3 >.....................A# • sb mm- 41 ................................... t&iR ##-mo mm-#* m^-w ##- (49 .................................................................................................mm m~ b m#- 59 1- 8 *EEB#©m©Sfitf-i«rE■?v> T-:£ft##1£©I?S-...........................Stg ##- 1- 9 Model Experiments of Ship Capsize in Astern Seas —Second Report — .....................3# mm • @£ #&-#A Z • J. P. Panjaitan • #*B g&A- iS5 #&-# ft-JSP SB-SB ##•■ 77 1-10 Non-Linear Periodic Motions of a Ship Running in Following and Quartering Seas ......................................................................................tSB Sf$ Dracos Vassalos- 89 i-ii i6z6=pcj3it-B Ro-Ro @=m©L .......................................5B w~-mm m- /nh a# • mm##...... 103 1-12 T y TV- h V y 7y #gS^M6So¥E@SiOU-ffl ..........................................................................................................................—S#?£ 119 1- 13 .................................*iB g-m-m# IEE-S1 SU • JH# E# • SB 3f93....... 125 ................................................................................................ MW S- • M/ll m#.......139 2- 1 3 # __ ..................¥Uj #fit-J» BS.......(S) 2-2 Sfr • ## des) 2- 3 mxm&mm < __ ..................................................................................#-me ze-* ......................(m) 2- 4 Prediction of Wave Drift Damping by a Higher Order BEM ...........................................................................Bin Teng • M • MM mk....... 183 2-5 b TFlyingFishJ ©%%#% __ ..................................................... /j\em z- w ss- urn m-m& mx.....(193 ) 2- 6 Water Entry Simulation of Free-Fall Lifeboat (2 nd Report : Effects of Acceleration on the Occupants) —Z# # * M. R. H. Khondoker • #_k #fT 205 OISmBUnON OF nre DOCUMENT IS UM.IMITH) (& DISCLAIMER Portions of this document may be illegible in electronic image products. Images are produced from the best available original document 1 1-1 ©SEiLlf ie* it Ba e ie* & e m %* IE* F 32: m** Numerical Simulation for Submerged Body Fitted with Hydrofoil by Boundary Element Method by Satoshi Masuda, Member, Yoshikazu Kasahara, Member Isao Ashidate, Member Summary Recently many kinds of high speed boats have been developed. The hydrofoil type is one of them. On considering the hydrofoil type, one important problem is interaction, for example, interaction between the main hull and the hydrofoil, the hydrofoil and the free surface etc. Here we consider the interaction between the free surface and a submerged lifting body by numerical simulation. The submerged lifting body is composed of a submerged body and a hydrofoil adapted to it. The numerical method is the Boundary Element Method (BEM) that was originally developed at Hiroshima Univer­ sity by Mori and Qi., We have modified the original method and have applied it to this case. We measured the lifting force and the pressure distribution on the hydrofoil in the NKK Tsu' Ship Model Basin, and confirmed that BEM is an effective method for the interaction problem between the free surface and a submerged lifting body. By using this BEM, we considered the depth effect of the lifting force of the submerged lifting body, the optimum location of the adapted hydrofoil and the optimum submerged body shape, <Dr£kW.i\y^OM&X%> -d So ¥E5n i. m 9 h k A-SiS MMt 9 y X—(TSL, Techno Super Liner) gro ?fir;btiTV>S „ (TSt-F265SD &0/J'M©t>0*^n o k < KSo*Vi-CViSo C©j:5 ± 3 S C k3 -ti: SifoS©b © kt, # ^•k.-ti:f^S!C^vxr^@k»S©»t, Sakffc **5^3© 2UT* 3 < ftSOEfb, # A&#©@af#R j: a. qeTK, MptfS k LT%*#©g3^ 85 m T 40 kt kUtiXIstCo f CT Fig. 12 © Type A -cum a aa*m©#2 \Z7xt J: 5 -kcb 0, * =F»K j: ? -C±U Sm©iB5iB<bmS>5 o$9 #*#©##i:S#*©#Ze%f$KJ:!)» #±3tirs„ %*#©#%!&#*&©#%ka ttiSiScpr S § ,,2,3,5) ayo-txMb @n-s,) * fc*KlS < fSffl 3 nx * NKKx.>*J-7 V v^a„_4-pEffl\*nmmmko =>-k «, ** NKK F S*rfSISfSKiSfCx3-ti:)i b ©T* a1,2,3>o C©##a- F %G15 ¥fig8¥5H 15, 16 E 2 H*31»Bgggl*a #179# $ya6SE^E*@Ki?nr, *4>g?28®±©E#tf-$i# dt- W(f) (8 ) itf, SJfHffl, SSSillLTltmSS k 3n 9n ©JtE&ESfrv^, 5tkiK, : ,_ H@|*> 6 %&**S©%HE j: 3S**? j: tir* t£^E± .M=iM.| e**» (9) dn dn L=o ©EAEW^O^SfilSUfco ko=g/Uo 2. ^ES>£©5tit-fb mrnmm ..._, zomvmvmM* ; H-SJSfOli*? Fig. 1©±5 K$»5„ ETmtSk GO) A#BkiBSL, $ S&SUSStfr Kutta ©#{$: > ;/ -Wi/ k T 3 k, SIBSSSB Laplace ©SStST-^S r'^re+—^rE-=const. ' (11) it3o '( -- 1 Cp TE+—Cp TE- (12) (1) i*s?B eo ^tb, %#gmmk u ^ y z ifrlRlB 3 ^©±^E5- S(l)Sr Green ggESS^TSSSr k i SfflH y^Ek^^JC-oviTBEF'Ci-^Srfflvi-C, 5$ c^=iH"7<&-i^("7)<fe (2) (6), (7)&#Wt. ga*EBRk«iadff k»3.CCT; Bm#@%SEb%^ES&L,y , ES©E8£f SS^TS^kST© J: -5 E»30 3/\ . 2/,+i.j+3Aj—6/,-i.j+/,-_2.j ^©Ak##m±©mEA©m#&#^.i * * « s, dx/t.'} ' 6/lx (13) #±©^[6]#%#^^ Hl/%, c B@EAK#f 3(&#A df\ _ fi.i+i —fi.j-i SB±.^('2)S, TENT teSfflv>T 1 ^©UtifSc-tbSS ,dy)u~ 2Ay........................... (14) (M-Y'JM-V ^ ° - ‘i ■ ’ i r : ' m'-fi, \dt ),-.j +\dt ),.j 2 faDri- 2-#-SE,=0 - P=1,2, -, W (3) (15) 0=1 0=1 aw , At 2 Kutta B5$(ll) %%^b©^{4=k L-C#m s^!Lt^ ■ ' ■ <-» V, ^(12) C33,ViTB#%1^?> Wake®©ASS D”-fLT4;(-4y* v - ,/.f :v(5),: SH-f 3 C kr##^(4=S#JSg#,3 3 kW#3o L* L-H^K Wake.ESS-fbS-STESU-SSfra © BM c©k@©%#&#BMT©i3caseins.f.&g m-#±mm-e&3. ^ 3 -r wake ®©mm Assm afnfn%m, g*s®-c©j&ss, mwnass*L, (/(/) Bum f E*B3&*#©#mmss*f. c, be *{SiScS^U T£+, T£- B*Em##-e©±m kT ES5v?"<, , . @A$E&*: , V, :z=? ■ ' - ' (6) f=I-«‘>f~if-f f ^ <" END Fig. 2 Flow of calculation sswfstae x o <p%mgfn 3 MOtotfr 'si'+n'*WE1r 3 £k c <t •? T, ZQ& E*-fe>-9 —SSffi±KS»a*,-HTffl*fToteo C©E, 0&#lBLA. E*4z y-9" —A?S@±Kj3Vi-tESK%e>^j;-5 CjbQX LA. 3-bm#E@»aA,A#, m@&#BLA. Fig. 3 <^TE+~ !t+a‘f>TE+ (16) KEft-fe y-9* —©EiHE^'fo iSScoviTtt-y- —tKS; 4>TE-K n_a<l>T£- (17) $ASAtej:y:£t*©rHI K-?WTG3#%#&mW%. Table 1 E#b#k^»©* a tt, 5$ (12) KOV»t Newton ©REl£&fflv>T8i$T3 ZttfTBZo BLfcOSWMH*©*) k5«3), (4), (5)*6fcA 4. # # Matrix T#< .Fig. 2 El+JJCsftft 0 ©atKotAt, a*#g Zwto %*##KK o t> Tsgg? £ an, n-tffimmzmtfr'pmofrtu mm*m e^.m-#^{4=(±Fk =0.713T, #KED©»'v*3-e-t±tSf njlSP k LT#Ef 3X h^y b mUELAo *###B Fig. 12 © Type A k^3. *EE©SE'C,'kt 55%©feE£k L, ffl&t* 3° kT3. &A# tbLA. %sm©#%$cik«, %*#©mmmm t/0 k^*#©s 3. H^Sfc«tz>'#tHEE 5 Lpp S-fflUTfroA. 4.i :&^mm # S*#j3 <k K, MTeSSEOViTlffi&fToA (1) *4»RBm±<DEA (2) *m±©a##i iifLA. $A%R*@#KA. (3) 3 #|Rj©;£ij£# Fig. 4 EzKE^SSi k § 2§*ft©&*SI@: E J: m%mkLT, g+mta-c&3*Em#@%*#t* Table 1 Conditions of experiments and calculations <pm<D&(D2WM&m'fc, mt^?&3a*#©g@ Measured B.E.H aLpp=3.953m, S^WStt0.22m-C$,3„ $A*fR Submerged body Hydrofoil Submerged body Hydrofoil 6.#%}$-COEttB=1.674m, SSSgflSE#f 3 + Hvdrofoil + Hydrofoil d/Loo=0.06 O o o o Xt--Mt 1/21.5 k»3.C©k@A9#ka**6L< d/Lop=0.08 O O O o d/Lpp=0.10 o O o o Xh?y bKj:?-C##@il?W3. d/Lop=0.13 o o o o d/Loo=0.20 o o EBI±©EABtE K ttEE 6 mm, SfSSffil.O kg/cm 2 © d/Loo=0.25 o o Hydrofoil o Sensor position Submerged body Fig. 3 Position of pressure measuring sensors A wmx&g&xsk mm# mesured by load cell (Hydrofoil) mesured by pressure measuring sensor (Hydrofoil) r cal by B.BM / '(Submerged body + Hydrofoil) cal by B£M ___ (Hydrofoil) —■ " __.—' caL bv B£M ^ (Submerged body + Hydrofoil) mesured, by , load cell ; [Submerged body -s + Hydrofoil) mesured by pressure measuring sensor (Submerged body + Hydrofoi) Fig. 4 Cl for each submergence depth thifflwa-vr,Fig. 5 if fcSiSEi,5 EMitKioT**/; #@±©E/7E/F^^f. Fig.6 Ea*^m##©#e© m^©#A& 0 k LT Span;Wd©±®kT®© 8K#©-?-?#, vr*»f£„ ©s§tE± stf^nas^u mmo ©v-^ bthcihi r#*7c-fk $ o , k mnm.b%mm&M?z>b, \iC&EzM###@*#EStttoEttS; < *5KifS±®©E#**;*:§ < *o, cxm^m^vx^-s®^^5„ vi-5, SatoKttth$?iakEASi5)-EJ: 5g*iiJ: <-$$( T@-CttZ§:*^K©^E J;SEAWstittdxS t>„ ## k R# @ %*#E O V^TE A^A©^ &fr ^ w. ztumnm15%mmsm±©aa©*&#*.; % k, *^m#m©^m±®©EA^#^-1s„ _ Fig. 5 ©±5 EH-mSSkSWgm&WBL T&gt £1t e,fL3. 6akA,s@%mm©m@©#m6m-gk%&. t©a S1 ©ti&kiS^SSa* 0.08 ©i§£-Ctt, ttjo ± %- nfca>e.**E^S®EAIhifflE«:»SERIES 35%ggW>LTt^B kA%^S. o*0&*i$E*VJx _ fc. EE^S®Sf>i,. a%d#R%BSE#L-C S <»5kg6g@-CJ:9*#£z&£#9, f©®fCi #© Ag#m k ir) 9 ®a^ g, ^ f 3 C k &#© 6 vx ■oX^M(omtJ*mT-t^c ttz, ^*8#@&!k#k 3.
Load more

Recommended publications
  • Evaluation of Ultimate Ship Hull Strength R
    ,sc., nC,$ THE SOCIETYOF NAVALARCHITECTSAND MARINE ENGINEERS . OneWorldTrade Center,Suit. 1369, NewYork, N.Y. 10048 # “+ ~ PaPer,tobe PresentedatExtremeLoad,Res$mseSymDosium 8 : Arl,mton,VA,October1>20,1981 ;$ 01! # “o, & o*H,.S,** Evaluation of Ultimate Ship Hull Strength R. S. Dow, R. C. Hugill, J, D. Clark and C. S. Smith, Admiralty Marine Technology Establishment, Glasgow, Scotland ABSTRACT plastic strength of ships’ hulls (1 to 6)* and a method of estimating hull strength has been The problem of evaluating the U1timate proposed (4) which takes account of local buck- longitudinal strength of a ship’s hull is dis- ling failure and [email protected]~f10@ cussed. In addition to behaviour under quasi- carrying capacity in elements of the hull cross- static loads, the whipping response of a section. The purpose of the present paper is ship’s hull to impulsive loads, eg bow- to examine the accuracy of this approach by slamming and underwater explosions, is con- correlation of analysis with collapse tests on sidered. A method of analysis is described, various longitudinally stiffened steel box- based on approximate characterization of the girders and to consider extension of the strength of elements of hul1 cross-sections analysis method to deal with the case of under tensile and compressive loads associated dynamic loading, in particular whipping of the with hull-girder bending togetherwith local hull girder caused by bow-slamming or under- lateral-pressureeffects. The influence of water explosions which, as shown by recent imperfections (initial deformations and theoretical studies and seakeeping trials, may residual stresses) is accounted for. The cause severe midship bending moments.
    [Show full text]
  • Ultimate Strength
    16 th INTERNATIONAL SHIP AND OFFSHORE STRUCTURES CONGRESS 20-25 AUGUST 2006 SOUTHAMPTON, UK VOLUME 1 COMMITTEE III.1 ULTIMATE STRENGTH COMMITTEE MANDATE Concern for ductile behaviour of ships and offshore structures and their structural components under ultimate conditions. Attention shall be given to the influence of fabrication imperfections and in-service damage and degradation on reserve strength. Uncertainties in strength models for design shall be highlightened COMMITTEE MEMBERS Chairman: T Yao E Brunner S R Cho Y S Choo J Czujko S F Estefen J M Gordo P E Hess H Naar Y Pu P Rigo Z Q Wan KEYWORDS Ultimate strength, buckling strength, yielding strength, nonlinear analysis, steel structures, aluminium structures, composite structures, ship structures, offshore structures, initial imperfections, in-service degradation, uncertainties, reliability, static/quasi-static loads 369 ISSC Committee III.1: Ultimate Strength 371 CONTENTS 1. INTRODUCTION ....................................................................................................373 2. FUNDAMENTALS..................................................................................................375 3. EMPIRICAL AND ANALYTICAL METHODS....................................................378 3.1 Unstiffened and Stiffened Plates..................................................................378 3.2 Tubular Members and Joints........................................................................381 3.3 Shells ............................................................................................................382
    [Show full text]
  • Husker Sports Network 2007 Nebraska Stations Huskers on Radio Ainsworth, KBRB-AM
    College Football’s Winningest Program Since 1970 HUSKER SPORTS NETWORK 2007 Nebraska Stations Huskers on Radio Ainsworth, KBRB-AM .......................................... 1400 The Husker Sports Network came under new ownership in the fall of 2006, as Host Communications acquired Alliance, KCOW-AM ............................................ 1400 the former Pinnacle Sports Network. Aurora, KRGY-FM................................................. 97.3 A well-known entity throughout college athletic marketing circles, Host Communications Inc. has marketing Beatrice, KWBE-AM ............................................ 1450 agreements with seven universities as well as the Southeastern Conference and NCAA Football. The Lexington, Broken Bow, KCNI-AM/KBBN-FM ............... 1280/98.3 Ky.-based company also manages five associations, more than 30 web sites and has a publishing division that Chadron, KCSR-AM .............................................. 610 produces 700 publications annually, including all NCAA championship game-day programs. 1 0 Columbus, KJSK-AM ............................................. 900 HOST is a subsidiary of Triple Crown Media, Inc. TCMI owns and operates six daily newspapers with a total Falls City, KTNC-AM/KLZA-FM ................. 1230/101.3 daily circulation of about 120,000. TCMI is a public company traded on NASDAQ and based in Lexington, Ky. Fremont, KHUB-AM/KFMT-FM .................. 1340/105.5 The Husker Sports Network will continue the strong tradition of broadcasting excellence established by the Grand Island, KRGI-AM ....................................... 1430 Pinnacle Sports Network, which had produced and marketed live broadcasts of University of Nebraska football, Hastings, KLIQ-FM ............................................... 94.5 men’s and women’s basketball, volleyball, baseball and softball games for the past 11 years. Pinnacle was first Hastings, KHAS-AM ............................................ 1230 awarded the rights on Feb. 9, 1996, and the University renewed the contract on Aug.
    [Show full text]
  • Ultimate and Residual Strength Assessment of Ship Structures
    CHALMERS UNIVERSITY OF TECHNOLOGY Gothenburg, Sweden www.chalmers.se LICENTIATE THESIS ARTJOMS KUZNECOVS U ltimate and Residual Strength Assessment of Ship Structures Ultimate and Residual Strength Assessment of Ship Structures ARTJOMS KUZNECOVS DEPARTMENT OF MECHANICS AND MARITIME SCIENCES CHALMERS UNIVERSITY OF TECHNOLOGY 2 020 Gothenburg, Sweden 2020 www.chalmers.se THESIS FOR THE DEGREE OF LICENTIATE OF ENGINEERING Ultimate and Residual Strength Assessment of Ship Structures ARTJOMS KUZNECOVS Department of Mechanics and Maritime Sciences CHALMERS UNIVERSITY OF TECHNOLOGY Gothenburg, Sweden 2020 Ultimate and Residual Strength Assessment of Ship Structures ARTJOMS KUZNECOVS © ARTJOMS KUZNECOVS, 2020 Report No 2020:07 Chalmers University of Technology Department of Mechanics and Maritime Sciences Division of Marine Technology SE-412 96, Gothenburg Sweden Telephone: + 46 (0)31-772 1000 Printed by Chalmers Reproservice Gothenburg, Sweden 2020 Ultimate and Residual Strength Assessment of Ship Structures ARTJOMS KUZNECOVS Chalmers University of Technology Department of Mechanics and Maritime Sciences Division of Marine Technology Abstract The prevention of ship structural failures and reduction of accident consequences contribute to increased safety at sea and reduced environmental impact. A need for reliable and efficient ship designs facilitates knowledge accumulation and the development of tools for the assessment of hull structural responses to acting loads. Important in this regard, ship design criteria are the ultimate and residual strengths of a hull that determine whether a ship may be safely operated in intact and accidentally damaged conditions. Thus, an accurate and reliable procedure for estimating a ship’s strength accounting for all actual foreseeable scenarios and reasonably practicable conditions is necessary. The main objective of this thesis is to develop a new precise and time-efficient methodology for the assessment of the ultimate and residual strength under vertical and biaxial loading conditions.
    [Show full text]
  • Analysis of Ultimate Capacity of the Structural Elements of Single Hull VLCC Subject to Corrosion
    Analysis of ultimate capacity of the structural elements of single hull VLCC subject to corrosion Rachid DAMI Master Thesis Presented in partial fulfillment of the requirements for the double degree: “Advanced Master in Naval Architecture” conferred by University of Liege "Master of Sciences in Applied Mechanics, specialization in Hydrodynamics, Energetic and Propulsion” conferred by Ecole Centrale de Nantes developed at West Pomeranian University of Technology, Szczecin in the framework of the “EMSHIP” Erasmus Mundus Master Course in “Integrated Advanced Ship Design” Ref. 159652-1-2009-1-BE-ERA MUNDUS-EMMC Supervisor: Dr.Maciej Taczala, West Pomeranian University of Technology, Szczecin Reviewer: Dr.Eng. Patrick Kaeding, University Rostock Szczecin, February 2012 Analysis of ultimate capacity of the structural elements of single hull VLCC subject to corrosion 3 ABSTRACT During the last few decades, the emphasis in structural design has been moving from the allowable stress design to the limit state design, because the latter approach has many more advantages. A limit state is formally defined as a condition for which a particular structural member or an entire structure fails to perform the function that it has been designed for. In order to ensure critical for economy and safe design of a ship’s hull, it is necessary to accurately evaluate the capacity of the hull girder considering extreme loads. The objective of this project is to perform the strength analysis for tank structures, according to the Det Norske Veritas (DNV) Rules and Regulations; following the IACS Common Structural Rules (CSR). The general plan and methodology of the project are presented in the report (dissertation).
    [Show full text]
  • Exploring the Atom's Anti-World! White's Radio, Log 4 Am -Fm- Stations World -Wide Snort -Wave Listings
    EXPLORING THE ATOM'S ANTI-WORLD! WHITE'S RADIO, LOG 4 AM -FM- STATIONS WORLD -WIDE SNORT -WAVE LISTINGS WASHINGTON TO MOSCOW WORLD WEATHER LINK! Command Receive Power Supply Transistor TRF Amplifier Stage TEST REPORTS: H. H. Scott LK -60 80 -watt Stereo Amplifier Kit Lafayette HB -600 CB /Business Band $10 AEROBAND Solid -State Tranceiver CONVERTER 4 TUNE YOUR "RANSISTOR RADIO TO AIRCRAFT, CONTROL TLWERS! www.americanradiohistory.com PACE KEEP WITH SPACE AGE! SEE MANNED MOON SHOTS, SPACE FLIGHTS, CLOSE -UP! ANAZINC SCIENCE BUYS . for FUN, STUDY or PROFIT See the Stars, Moon. Planets Close Up! SOLVE PROBLEMS! TELL FORTUNES! PLAY GAMES! 3" ASTRONOMICAL REFLECTING TELESCOPE NEW WORKING MODEL DIGITAL COMPUTER i Photographers) Adapt your camera to this Scope for ex- ACTUAL MINIATURE VERSION cellent Telephoto shots and fascinating photos of moon! OF GIANT ELECTRONIC BRAINS Fascinating new see -through model compute 60 TO 180 POWER! Famous actually solves problems, teaches computer Mt. Palomar Typel An Unusual Buyl fundamentals. Adds, subtracts, multiplies. See the Rings of Saturn, the fascinating planet shifts, complements, carries, memorizes, counts. Mars, huge craters on the Moon, phases of Venus. compares, sequences. Attractively colored, rigid Equat rial Mount with lock both axes. Alum- plastic parts easily assembled. 12" x 31/2 x inized overcoated 43/4 ". Incl. step -by -step assembly 3" diameter high -speed 32 -page instruction book diagrams. ma o raro Telescope equipped with a 60X (binary covering operation, computer language eyepiece and a mounted Barlow Lens. Optical system), programming, problems and 15 experiments. Finder Telescope included. Hardwood, portable Stock No. 70,683 -HP $5.98 Postpaid tripod.
    [Show full text]
  • Nebraska(4-5, 2-4) Vs. #15 Wisconsin (7-2, 4-2
    NEBRASKA 2019 FOOTBALL GAME NOTES NEBRASKA (4-5, 2-4) VS. #15 WISCONSIN (7-2, 4-2) SATURDAY, NOV. 16, 2019 • 11 A.M. CT • LINCOLN, NEB. MEMORIAL STADIUM • CAPACITY: 85,458 • SURFACE: FIELDTURF Nebraska begins the home stretch of its 2019 season on Saturday when the Huskers take on Wisconsin NEBRASKA at Memorial Stadium in a Big Ten West clash. The game is set to kick off shortly after 11 a.m. and will be televised by BTN. The game can be heard on the Husker Sports Network from Learfield-IMG. • 2019 Record: 4-5, 2-4 • Last Game: Purdue (L, 31-27) Nebraska will enter the contest with a 4-5 record and a 2-4 mark in Big Ten Conference play. The Huskers • Streak: Lost 3 have three remaining games, with Big Ten West matchups against Wisconsin and Iowa sandwiched • AP Rank: Not Ranked around a trip to Maryland. Nebraska enters the home stretch needing two victories in its final three • Coaches Rank: Not Ranked games to reach bowl eligibility. • Head Coach: Scott Frost Nebraska Record: The Huskers are coming off a bye which was preceeded by a 31-27 loss at Purdue on Nov. 2. NU took a • 8-13 (2nd year) Career Record: lead in the final five minutes in West Lafayette, but Purdue scored a late touchdown to pull out the victory. • 27-20 (4th year) • Record vs. Wisconsin: 0-1 Wisconsin comes into the game with a 7-2 overall record, and a 4-2 mark in the Big Ten Conference. The Badgers are in second place in the conferene's West Division and remain in contention for a trip to the the Big Ten Championship Game in Indianapolis.
    [Show full text]
  • An Analysis of the Study of Mechanical Properties and Microstructural Relationship of HSLA Steels Used in Ship Hulls
    World Maritime University The Maritime Commons: Digital Repository of the World Maritime University World Maritime University Dissertations Dissertations 2007 An analysis of the study of mechanical properties and microstructural relationship of HSLA steels used in ship hulls Htay Aung World Maritime University Follow this and additional works at: https://commons.wmu.se/all_dissertations Digital Par t of the Mechanical Engineering Commons Commons Network Recommended Citation Logo Aung, Htay, "An analysis of the study of mechanical properties and microstructural relationship of HSLA steels used in ship hulls" (2007). World Maritime University Dissertations. 190. https://commons.wmu.se/all_dissertations/190 This Dissertation is brought to you courtesy of Maritime Commons. Open Access items may be downloaded for non-commercial, fair use academic purposes. No items may be hosted on another server or web site without express written permission from the World Maritime University. For more information, please contact [email protected]. WORLD MARITIME UNIVERSITY Malmö, Sweden AN ANALYSIS OF THE STUDY OF MECHANICAL PROPERTIES AND MICROSTRUCTURAL RELATIONSHIP OF HSLA STEELS USED IN SHIP HULLS By HTAY AUNG The Union of Myanmar A dissertation submitted to the World Maritime University in partial Fulfilment of the requirements for the award of the degree of MASTER OF SCIENCE In MARITIME AFFAIRS (MARITIME EDUCATION AND TRAINING) 2007 © Copyright HTAY AUNG, 2007. DECLARATION I certify that all the material in this dissertation that is not my own work has been identified, and that no material is included for which a degree has previously been conferred on me. The contents of this dissertation reflect my own personal views, and are not necessarily endorsed by the University.
    [Show full text]
  • A Simplified Approach to Estimate the Ultimate Longitudinal Strength of Ship Hull
    130 Journal of Marine Science and Technology, Vol. 11, No. 3, pp. 130-148 (2003) A SIMPLIFIED APPROACH TO ESTIMATE THE ULTIMATE LONGITUDINAL STRENGTH OF SHIP HULL Hsin-Chuan Kuo* and Jiang-Ren Chang** Key words: simplified approach, ultimate longitudinal strength, hull girder, “collapse” have been identified as responses to an ex- stiffened panel. cessive hull girder bending moment. These may take place, presumably, with but a single application of load so that the possibility of their occurring must be weighted ABSTRACT against the extreme or worst likely load value. In additions, because aging ships may have suffered dam- In this paper, the calculation of the ultimate longitudinal strength ages due to hull corrosion and fatigue, their structural of the ship hull is revisited. A simplified approach dealing with the longitudinal ultimate strength of ship hull has been developed and an resistance may weaken and further collapse under ap- effective numerical program is implemented based on the individual plied loads even smaller than designed loads. components of ship structures. It is, then, possible to find the ultimate The conventional longitudinal strength calcula- strength of the whole ship structure by evaluating those individual tion for a ship mainly concerns the elastic response of components. Comparisons of numerical results from the proposed hull girder due to an assumed wave load and then, the approach and published literatures are conducted for further validation. Since relative errors of calculations of the current approach to the elastic section modulus of hull girder, which is taken as literature with respect to the experimental data are within 3%, it is the primary surveying index of the longitudinal bending shown that the proposed approach can be adopted for the estimation strength, can be achieved by using the linear bending of the ultimate bending strength of ship hull in sagging or hogging theory.
    [Show full text]
  • Ultimate Longitudinal Strength of Composite Ship Hulls
    Curved and Layer. Struct. 2017; 4:158–166 Research Article Open Access Xiangming Zhang*, Lingkai Huang, Libao Zhu, Yuhang Tang, and Anwen Wang Ultimate Longitudinal Strength of Composite Ship Hulls DOI 10.1515/cls-2017-0012 posite materials. There are now all-composite naval ships Received Dec 15, 2016; accepted Mar 12, 2017 in service. Longitudinal bending moment carried by ship hull Abstract: A simple analytical model to estimate the lon- girder increasing with the increasing length of composite gitudinal strength of ship hulls in composite materials ship hulls, the ship safety related to longitudinal ultimate under buckling, material failure and ultimate collapse is strength becomes more important at design. According to presented in this paper. Ship hulls are regarded as as- traditional ship design rules, the longitudinal strength of semblies of stiffened panels which idealized as group of the ship hull built of steel with length exceeding 60 m plate-stiffener combinations. Ultimate strain of the plate- must be assessed. The stiffness of composite materials is stiffener combination is predicted under buckling or ma- generally low. Longitudinal deformation of ship hulls in terial failure with composite beam-column theory. The ef- composite materials is usually larger than that built of fects of initial imperfection of ship hull and eccentricity of steel. Recent years, with the rapid development trend and load are included. Corresponding longitudinal strengths momentum of construction of large-scale and super large of ship hull are derived in a straightforward method. A composite ship hulls, the length of ship hulls in composite longitudinally framed ship hull made of symmetrically materials are increasing so that the study of longitudinal stacked unidirectional plies under sagging is analyzed.
    [Show full text]
  • ULTIMATE STRENGTH of HULL GIRDER for PASSENGER SHIPS Doctoral Dissertation
    TKK Dissertations 22 Espoo 2006 ULTIMATE STRENGTH OF HULL GIRDER FOR PASSENGER SHIPS Doctoral Dissertation Hendrik Naar Helsinki University of Technology Department of Mechanical Engineering Ship Laboratory TKK Dissertations 22 Espoo 2006 ULTIMATE STRENGTH OF HULL GIRDER FOR PASSENGER SHIPS Doctoral Dissertation Hendrik Naar Dissertation for the degree of Doctor of Science in Technology to be presented with due permission of the Department of Mechanical Engineering for public examination and debate in Auditorium 216 at Helsinki University of Technology (Espoo, Finland) on the 10th of March, 2006, at 12 noon. Helsinki University of Technology Department of Mechanical Engineering Ship Laboratory Teknillinen korkeakoulu Konetekniikan osasto Laivalaboratorio Distribution: Helsinki University of Technology Department of Mechanical Engineering Ship Laboratory P.O. Box 5300 (Tietotie 1) FI - 02015 TKK FINLAND URL: http://www.tkk.fi/Units/Ship/ Tel. +358-(0)9-4511 Fax +358-(0)9-451 4173 E-mail: [email protected] © 2006 Hendrik Naar ISBN 951-22-8028-0 ISBN 951-22-8029-9 (PDF) ISSN 1795-2239 ISSN 1795-4584 (PDF) URL: http://lib.tkk.fi/Diss/2006/isbn9512280299/ TKK-DISS-2101 Picaset Oy Helsinki 2006 AB HELSINKI UNIVERSITY OF TECHNOLOGY ABSTRACT OF DOCTORAL DISSERTATION P. O. BOX 1000, FI-02015 TKK http://www.tkk.fi Author Hendrik Naar Name of the dissertation Ultimate Strength of Hull Girder for Passenger Ships Date of manuscript 12.09.2005 Date of the dissertation 10.03.2006 Monograph Article dissertation (summary + original articles) Department Department of Mechanical Engineering Laboratory Ship Laboratory Field of research Strength of materials Opponent(s) Preben Terndrup Pedersen, Ivo Senjanović Supervisor Petri Varsta (Instructor) Petri Varsta Abstract The ultimate strength of the hull girder for large passenger ships with numerous decks and openings was investigated.
    [Show full text]
  • Draft Copy « License Modernization «
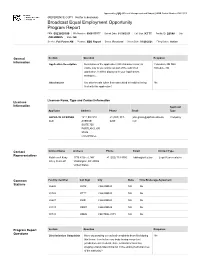
    Approved by OMB (Office of Management and Budget) | OMB Control Number 3060-0113 (REFERENCE COPY - Not for submission) Broadcast Equal Employment Opportunity Program Report FRN: 0023600190 File Number: 0000133377 Submit Date: 01/28/2021 Call Sign: KTTT Facility ID: 28148 City: COLUMBUS State: NE Service: Full Power AM Purpose: EEO Report Status: Received Status Date: 01/28/2021 Filing Status: Active General Section Question Response Information Application Description Description of the application (255 characters max.) is Columbus, NE SEU visible only to you and is not part of the submitted Schedule 396 application. It will be displayed in your Applications workspace. Attachments Are attachments (other than associated schedules) being No filed with this application? Licensee Name, Type and Contact Information Licensee Information Applicant Applicant Address Phone Email Type ALPHA 3E LICENSEE 1211 SW 5TH +1 (503) 517- john.grossi@alphamediausa. Company LLC AVENUE 6200 com SUITE 750 PORTLAND, OR 97204 United States Contact Contact Name Address Phone Email Contact Type Representatives Kathleen A Kirby 1776 K Street, NW +1 (202) 719-3360 [email protected] Legal Representative Wiley Rein LLP Washington, DC 20006 United States Common Facility Identifier Call Sign City State Time Brokerage Agreement Stations 26628 KJSK COLUMBUS NE No 28148 KTTT COLUMBUS NE No 26627 KLIR COLUMBUS NE No 28149 KKOT COLUMBUS NE No 50733 KZEN CENTRAL CITY NE No Program Report Section Question Response Questions Discrimination Complaints Have any pending or resolved
    [Show full text]