MUSIC and COMBINATIONS1 Tom JOHNSON2
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

A Comparative Analysis of the Six Duets for Violin and Viola by Michael Haydn and Wolfgang Amadeus Mozart
A COMPARATIVE ANALYSIS OF THE SIX DUETS FOR VIOLIN AND VIOLA BY MICHAEL HAYDN AND WOLFGANG AMADEUS MOZART by Euna Na Submitted to the faculty of the Jacobs School of Music in partial fulfillment of the requirements for the degree, Doctor of Music Indiana University May 2021 Accepted by the faculty of the Indiana University Jacobs School of Music, in partial fulfillment of the requirements for the degree Doctor of Music Doctoral Committee ______________________________________ Frank Samarotto, Research Director ______________________________________ Mark Kaplan, Chair ______________________________________ Emilio Colón ______________________________________ Kevork Mardirossian April 30, 2021 ii I dedicate this dissertation to the memory of my mentor Professor Ik-Hwan Bae, a devoted musician and educator. iii Table of Contents Table of Contents ............................................................................................................................ iv List of Examples .............................................................................................................................. v List of Tables .................................................................................................................................. vii Introduction ...................................................................................................................................... 1 Chapter 1: The Unaccompanied Instrumental Duet... ................................................................... 3 A General Overview -

Composed for Six-Hands Piano Alti El Piyano Için Bestelenen
The Turkish Online Journal of Design, Art and Communication - TOJDAC ISSN: 2146-5193, April 2018 Volume 8 Issue 2, p. 340-363 THE FORM ANALYSIS OF “SKY” COMPOSED FOR SIX-HANDS PIANO Şirin AKBULUT DEMİRCİ Assoc. Prof. Education Faculty, Music Education Faculty. Uludag University, Turkey https://orcid.org/0000-0001-8904-4920 [email protected] Berkant GENÇKAL Assoc. Prof. State Conservatory, School for Music and Drama. Anadolu University, Turkey https://orcid.org/0000-0001-5792-2100 [email protected] ABSTRACT The piano, which is a solo instrument that takes part in educational process, can take role not only in instrumental education but also in chamber music education as well with the 6-hands pieces for three players that perform same composition on a single instrument. According to the international 6-hands piano literature, although the works of Alfred Schnittke's Hommage, Carl Czerny's Op.17 and 741, Paul Robinson's Pensees and Montmartre and many more are included, the Turkish piano literature has been found to have a limited number of compositions. The aim of the work is to contribute to the field by presenting musical analysis about the place and the importance of the educational use of the works composed for 6-hands which are extremely rare in the Turkish piano literature. As an example, the piece named Sky composed by Hasan Barış Gemici is considered. Analysis is supported by comparative methods in form, structuralism, rhythm, theoretical applications and performance; it also gives information about basic playing techniques. It is thought that this study carries importance in contributing to the limited number of Turkish 6-hands piano literature and researchers who will conduct research in this regard, in terms of creating resources for performers and composers who will interpret the literature. -

Download Program Notes
Notes on the Program By James M. Keller, Program Annotator, The Leni and Peter May Chair Piano Quintet in F minor, Op. 34 Johannes Brahms ohannes Brahms was 29 years old in 1862, seated at the other piano. Ironically, critics Jwhen he embarked on this seminal mas- now complained that the work lacked the terpiece of the chamber-music repertoire, sort of warmth that string instruments would though the work would not reach its final have provided — the opposite of Joachim’s form as his Piano Quintet until two years objection. Unlike the original string-quintet later. He was no beginner in chamber music version, which Brahms burned, the piano when he began this project. He had already duet was published — and is still performed written dozens of ensemble works before and appreciated — as his Op. 34bis. he dared to publish one, his B-major Piano By this time, however, Brahms must have Trio (Op. 8) of 1853–54. Among those early, grown convinced of the musical merits of his unpublished chamber pieces were 20-odd material and, with some coaxing from his string quartets, all of which he consigned friend Clara Schumann, he gave the piece to destruction prior to finally publishing his one more try, incorporating the most idiom- three mature works in that classic genre in atic aspects of both versions. The resulting the 1870s. In truth, he did get some use out Piano Quintet, the composer’s only essay of those early quartets — to paper the walls in that genre (and no wonder, after all that and ceilings of his apartment. -
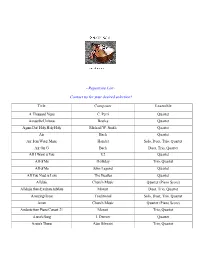
Repertoire List~
~Repertoire List~ Contact us for your desired selection! Title Composer Ensemble A Thousand Years C. Perri Quartet Across the Universe Beatles Quartet Agnus Dei/Holy Holy Holy Michael W. Smith Quartet Air Bach Quartet Air from Water Music Handel Solo, Duet, Trio, Quartet Air On G Bach Duet, Trio, Quartet All I Want is You U2 Quartet All of Me Holliday Trio, Quartet All of Me John Legend Quartet All You Need is Love The Beatles Quartet Alleluia Church Music Quartet (Piano Score) Allelujia from Exultate Jubilate Mozart Duet, Trio, Quartet Amazing Grace Traditional Solo, Duet, Trio, Quartet Amen Church Music Quartet (Piano Score) Andante from Piano Concert 21 Mozart Trio, Quartet Annie’s Song J. Denver Quartet Annie’s Theme Alan Silvestri Trio, Quartet Apollo 13 Horner Quartet Appalachia Waltz O’Connor Trio, Quartet Arioso Bach Solo, Duet, Trio, Quartet Arrival of the Queen of Sheba Handel Trio, Quartet Ashokan Farewell Jay Ungar Quartet (Piano Score) At Last Harry Warren Quartet Ave Maria Bach-Gounod Solo, Duet, Trio, Quartet Ave Maria (A flat) Schubert Quartet (Piano Score) Ave Maria (B flat) Schubert Quartet Ave Verum Corpus Mozart Solo, Duet, Trio, Quartet (plus Piano Score) Barcarolle from Tales of Hoffman Offenbach Quartet Be Thou My Vision Traditional Duet, Trio, Quartet Beauty and the Beast Ashman Quartet Bei Mennern from The Magic Flute Mozart Quartet Best Day of My life American Authors Quartet Bist du bei mer Bach Trio, Quartet Bittersweet Symphony M. Jagger Quartet Blessed are They Church Music Quartet Blessed are Those Who Love You Haugen Quartet (Piano Score) Blue Moon Rodgers Quartet Born Free Barry Quartet Bourree Bach Solo, Duet, Trio, Quartet Bourree Handel Solo, Duet, Trio, Quartet Brandenburg Concerto No. -

Memorandum LIBRARY of CONGRESS
UNITED STATES GOVERNMENT Memorandum LIBRARY OF CONGRESS 5JSC/LC/12 TO: Joint Steering Committee for Development of RDA DATE: February 6, 2008 FROM: Barbara B. Tillett, LC Representative SUBJECT: Proposed revision of RDA chap. 6, Additional instructions for musical works and expressions The Library of Congress is submitting rule revision proposals for the RDA December 2007 draft chapter 6 instructions for musical works and expressions. Goals of proposals 1. To maintain the additional instructions for music intact (although LC recommends integrating them with the general instructions after the first release of RDA). 2. To fill in gaps in the AACR2 rules carried over into RDA by a. Incorporating selected AACR2 rule revisions; b. Adding instructions that clarify, make explicit, or expand some principles and instructions carried over from AACR2; c. Proposing new instructions. 3. To simplify some unnecessarily complex instructions. 4. To arrange certain subsections in the six major instructions in a more logical way, based wherever possible on principles that group together types of resources having common characteristics. 5. To revise the instructions for medium of performance to provide for all media found in resources and to do that using vocabulary that adheres as closely as possible to the principle of representation: incorporating words the composer or resource uses. 6. To revise or eliminate instructions LC finds unworkable based on past experience with AACR2 (e.g., the instructions for key (6.22) in section M of this document). 7. In the interest of simplification, to eliminate vexing terms catalogers have spent inordinate amounts of time interpreting when using AACR2 (e.g., “type of composition” as a formal term when all it need be is a useful phrase; “score order”). -

Music 130-205 Piano Ensemble
Music 130-205: Chamber Music Workshop Piano (Piano Ensemble) Syllabus – Spring 2013 Director: Pamela Cordle My Office: CAB-1038 Telephone: (910) 392-2721 Email: [email protected] Class Time: Tuesdays and Thursdays, 5:00-6:15 pm Class Location: CAB-1019 (piano lab) Class meets initially in the digital piano lab. We move into practice rooms as needed. Our Goal: We will explore, study, prepare, and successfully perform piano literature composed for one piano-four hands (duet), one piano-six hands (trio), two pianos-four hands (duo), and two pianos-eight hands (quartet). This course is designed to improve piano sight-reading skills, enhance musicianship, improve interpretive skills, and review good performance practice for piano music. The culmination of the semester is a performance in Beckwith Recital Hall on Sunday, April 14, 2013 at 7:30. Attendance policy: Attendance is required! Be on time at the beginning of each rehearsal and stay until the end. The success of the ensemble depends on quality practice time and efficient, effective rehearsal techniques by all members. Except in emergencies, absences will not be excused. Exceptions may be made in the case of contagious or extended illness, but only if you have notified me in advance of the absence. If you have to miss and wish to be excused, use the phone number listed above. Please leave a voice message explaining the reason for your absence. If you share music, deliver the score for your partner before rehearsal. If you have to miss class, you are responsible for asking for and practicing assignments you may have missed. -

Evaluationof a Method for Separating Digitized Duet Signals*
PAPERS i Evaluationof a Method for Separating Digitized Duet Signals* ROBERT C. MAHER Department of Electrical Engineering, University of Nebraska-Lincoln, Lincoln, NE 68588-0511, USA A new digital signal-processing method is presented for separating two monophonic musical voices in a digital recording of a duet. The problem involves time-variant spectral analysis, duet frequency tracking, and composite signal separation. Analysis is performed using a quasi-harmonic sinusoidal representation based on short-time Fourier transform techniques. The performance of this approach is evaluated using real and artificial test signals. Applications include background noise reduction in live recordings, signal restoration, musicology, musique concrete, and digital editing, splicing, or other manipulations. 0 INTRODUCTION criteria may be identified. If two interfering signals occupy nonoverlapping frequency bands, for example, Separation of superimposed signals is a problem of the separation problem can be solved by using fre- interest in audio engineering. For example, it would quency-selective filters. In other cases the competing often be useful to identify and remove undesired in- signals may be described in a statistical sense, allowing terference (such as audience or traffic noise) present separation using correlation or a nonlinear detection during a live recording. Other examples include sep- method. However, most superimposed signals, such aration and replacement of errors in a recorded musical as two musical instruments playing simultaneously, do performance, separation of two simultaneous talkers not allow for such elementary decomposition methods, in a single communications channel, or even adjustment and other strategies applicable for signal separation of the level imbalance occurring when one musician must be discovered. -

The Critical Reception of Beethoven's Compositions by His German Contem- Poraries, V
The Critical Reception of Beethoven’s Compositions by His German Contemporaries, Op. 92 to Op. 100 Translated and edited by Robin Wallace © 2020 by Robin Wallace All rights reserved. ISBN 978-1-7348948-1-3 Center for Beethoven Research Boston University Contents Foreword 7 Op. 92. Symphony no. 7 in A Major 92.1 “Review.” 9 Allgemeine musikalische Zeitung 18 (27 November 1816): col. 817–22. 92.2 “Review” 20 Allgemeine musikalische Zeitung mit besonderer Rücksicht auf den österreichischen Kaiserstaat 1 (23 and 30 January 1817): 25–27, 37–40. 92.3 “News. Leipzig. Weekly Concerts in the Gewandhaussaal.” 26 Allgemeine musikalische Zeitung 19 (28 February 1817): col. 163. 92.4 “Fragment from Rosaliens Briefen an Serena, 27 Edited by Friedrich Mosengeil.” Allgemeine musikalische Zeitung 19 (26 March 1817): col. 217–22. 92.5 “This Year’s Concerts by the Philharmonic Society in London.” 31 Allgemeine musikalische Zeitung 24 (19 June 1822): col. 409. 92.6 “News. Strassburg.” 32 Allgemeine musikalische Zeitung 24 (28 August 1822): col. 570. 3 contents 92.7 “Aachen, 28 Feb.” 33 Stadt Aachener Zeitung (2 March 1823). 92.8 K. Br[eidenstein?]. 34 “The Lower Rhine Music Festival in Elberfeld, 1823.” Beiblatt der Kölnischen Zeitung 19 (1 June 1823). 92.9 C. Fr. Ebers 37 “Reflections.” Caecilia 2 (1825): 271–72. 92.10 “News. Cassel, 10 December 1827.” 39 Allgemeine Musikzeitung zur Beförderung der theoretischen und praktischen Tonkunst für Musiker und für Freunde der Musik überhaupt 1 (9 January 1828): 21–22. Op. 93. Symphony no. 8 in F Major 93.1 A. W. 41 “On Beethoven’s Newest Symphony.” Leipziger Kunstblatt für gebildete Kunstfreunde 1 (14 February 1818): 280. -

Piano Syllabus
Piano Syllabus Grade exams: Piano, Piano Accompanying Certificate exams: Piano Solo, Piano Duet, Piano Six Hands 2012–2014 Trinity College London 89 Albert Embankment London SE1 7TP UK T +44 (0)20 7820 6100 F +44 (0)20 7820 6161 E [email protected] www.trinitycollege.co.uk Charity number 1014792 Patron HRH The Duke of Kent KG Chief Executive Sarah Kemp Copyright © 2011 Trinity College London Published by Trinity College London Third impression, November 2012 Contents Introduction ................................................................................................................................... 3 Range of qualifications ......................................................................................................... 4 Grade exams — Piano, Piano Accompanying Structure ............................................................................................................................................. 5 Duration, Marking ............................................................................................................................ 6 Pieces ................................................................................................................................................... 7 Own Composition .............................................................................................................................8 Technical Work ................................................................................................................................ 9 Supporting Tests: -

Small Groups – Duets, Trios and Ensembles
SMALL GROUPS – DUETS, TRIOS AND ENSEMBLES PIANO DUET CLASSES - ONE PIANO FOUR HANDS max. 10 mins. Competitors may enter only one duet class, and they must enter at their grade level or higher. The competitor at the higher level will determine the level of eligibility. CLASS 08101 – 7 YRS & UNDER $25 Any duet from Two to Play, Book 1, Leaf, pub. FJH Music CLASS 08102 – 8 YRS & UNDER (PRE-GRADE 1) $25 Any duet from Hats Off to You, Bober, pub. FJH Music CLASS 08103 – GRADE 1 $25 Any duet from Two to Play, Book 2, Leaf, pub. FJH Music CLASS 08104 – GRADE 2 (own choice) $25 CLASS 08105 – GRADE 3 (own choice) $25 CLASS 08106 – GRADE 4 (own choice) $25 CLASS 08107 – GRADE 5 (own choice) $25 CLASS 08108 – GRADE 6 (own choice) $25 CLASS 08109 – GRADE 7 (own choice) $27 CLASS 08110 – GRADE 8 (own choice) $27 CLASS 08111 – GRADE 9 (own choice) $27 CLASS 08112 – GRADE 10 (own choice) $27 CLASS 08113 – ASSOCIATE/OPEN (own choice) $27 PIANO TRIO CLASSES max. 10 mins. The average age of the competitors will determine the level of entry. CLASS 08201 – TRIO - 10 YEARS & UNDER $25 CLASS 08202 – TRIO - 12 YEARS & UNDER $25 CLASS 08203 – TRIO - 14 YEARS & UNDER $25 CLASS 08204 – TRIO - 16 YEARS & UNDER $29 CLASS 08205 – TRIO - 18 YEARS & UNDER $29 VOCAL DUET Competitors may enter only one vocal duet class. The age of the older competitive will determine the level of the entry. CLASS 08301 – 8 YEARS & UNDER $25 CLASS 08302 – 10 YEARS & UNDER $25 CLASS 08303 – 12 YEARS & UNDER $25 CLASS 08304 – 14 YEARS & UNDER $25 CLASS 08305 – 16 YEARS & UNDER $27 CLASS 08306 – 18 YEARS & UNDER $27 CLASS 08307 – 20 YEARS & UNDER $27 CLASS 08308 – OPEN $27 VOCAL ENSEMBLE - Minimum of three, maximum of six singers Competitors may enter only one vocal ensemble class. -

Note, Pitch, Scale, Melody, Harmony, Chord, Score, Orchestration, Instrumentation, Overture, Aria, Recitative, Finale, Beat, Pulse, Octave
MUSIC AND COMPOSITION GLOSSARY CATEGORIES Composition: note, pitch, scale, melody, harmony, chord, score, orchestration, instrumentation, overture, aria, recitative, finale, beat, pulse, octave Writing: couplet, rhyming couplet, haiku, story, plot, narrative, libretto, dialogue, character, protagonist, antagonist, setting, detail Organizing words and music: stanza, phrase, chorus, refrain, form, key, ostinato, obbligato Organizing time: meter, rhythm, tempo, measure, time signature, largo, andante, allegro, accelerando, ritardando, rubato, fermata Notation: staff, treble clef, bass clef, whole note/rest, half note/rest, quarter note/rest, eighth note/rest, sixteenth note/rest, triplet, rest, fine, key signature Sounds: timbre, tone color Dynamics: legato, staccato, pianissimo, piano, forte, fortissimo, crescendo, diminuendo, decrescendo Singing: melisma, cadenza, improvisation, ornamentation, range, tessitura, solfège Vocal ranges: soprano, mezzo-soprano, contralto, tenor, baritone, bass Voicings: solo, duo, duet, trio, quartet, quintet, sextet, septet, octet, ensemble, chorus, tutti, unison DEFINITIONS accelerando: gradually becoming faster allegro: quick tempo, cheerful andante: moderate tempo antagonist: the chief opponent of the protagonist in a drama aria: lyric song for solo voice with orchestral accompaniment, generally expressing intense emotion baritone: a male singer with a middle tessitura bass: a male singer with a low tessitura bass clef: a symbol placed at the beginning of the lower staff to indicate the pitch of the notes -

St. Lawrence String Quartet
THE DINA KOSTON AND ROGER SHAPIRO FUND FOR nEW mUSIC IN tHE LIBRARY oF CONGRESS ST. LAWRENCE STRING QUARTET Friday, January 23, 2015 ~ 8 pm Coolidge Auditorium Library of Congress, Thomas Jefferson Building THE DINA KOSTON AND ROGER SHAPIRO FUND FOR NEW MUSIC Endowed by the late composer and pianist Dina Koston (1929-2009) and her husband, prominent Washington psychiatrist Roger L. Shapiro (1927-2002), the DINA KOSTON AND ROGER SHAPIRO FUND FOR NEW MUSIC supports commissions and performances of contemporary music. "LIKE" us at facebook.com/libraryofcongressperformingarts loc.gov/concerts Please request ASL and ADA accommodations five days in advance of the concert at 202-707-6362 or [email protected]. Latecomers will be seated at a time determined by the artists for each concert. Children must be at least seven years old for admittance to the concerts. Other events are open to all ages. • Please take note: Unauthorized use of photographic and sound recording equipment is strictly prohibited. Patrons are requested to turn off their cellular phones, alarm watches, and any other noise-making devices that would disrupt the performance. Reserved tickets not claimed by five minutes before the beginning of the event will be distributed to stand-by patrons. Please recycle your programs at the conclusion of the concert. The Library of Congress Coolidge Auditorium Friday, January 23, 2015 — 8 pm THE DINA KOSTON AND ROGER SHAPIRO FUND fOR nEW mUSIC IN tHE LIBRARY oF CONGRESS ST. LAWRENCE STRING QUARTET GEOFF NUTTALL & MARK FEWER, vIOLINS LESLEY ROBERTSON, vIOLA CHRISTOPHER COSTANZA, CELLO • Program FRANZ JOSEPH HAYDN (1732-1809) String Quartet in E-flat major, op.