DOCSLIB.ORG

A Study of Large Fringe and Non-Fringe Subtrees in Conditional Galton-Watson Trees Full Version

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Study of Large Fringe and Non-Fringe Subtrees in Conditional Galton-Watson Trees Full Version A study of large fringe and non-fringe subtrees in conditional Galton-Watson trees Full Version Xing Shi Cai, Luc Devroye School of Computer Science, McGill University of Montreal, Canada, [email protected] [email protected] October 8, 2018 We study the conditions for families of fringe or non-fringe subtrees to gw exist with high probability (whp) in Tn , a Galton-Walton tree of size n. gw We first give a Poisson approximation of fringe subtree counts in Tn , which permits us to determine the height of the maximal complete r-ary fringe subtree. Then we determine the maximal Kn such that every tree of size gw at most Kn appears as fringe subtree in Tn whp. Finally, we show that non-fringe subtree counts are concentrated and determine, as an application, gw the height of the maximal complete r-ary non-fringe subtree in Tn . 1 Introduction In this paper, we study the conditions for families of fringe or non-fringe subtrees to exist whp (with high probability) in a Galton-Walton tree conditional to be of size n. In particular, we want to find the height of the maximal complete r-ary fringe and non- fringe subtrees. We also want to determine the threshold kn such that all trees of size at most k appear as fringe subtrees. In doing so, we extend Janson's [22] result on fringe arXiv:1602.03850v1 [math.PR] 11 Feb 2016 n subtrees counts and prove a new concentration theorem for non-fringe subtree counts. Let T be the set of all rooted, ordered, and unlabeled trees, which we refer to as plane trees. All trees considered in this paper belong to T. (See Janson [21, sec. 2.1] for details.) Figure 1 lists all plane trees of at most 4 nodes. Given a tree T P T and a node v P T , let Tv denote the subtree rooted at v. We call 1 1 Tv a fringe subtree of T . If Tv is isomorphic to some tree T P T, then we write T “ Tv 1 Figure 1: Plane trees of at most 4 nodes. and say that T has a fringe subtree of shape T 1 rooted at v, or simply T contains T 1 as a fringe subtree. 1 On the other hand, if Tv can be made isomorphic to T by replacing some or none of 1 its own fringe subtrees with leaves (nodes without children), then we write T ă Tv and say that T has a non-fringe subtree of shape T 1 rooted at v, or simply T contains T 1 as a 1 1 non-fringe subtree. (Note that T “ Tv implies that T ă Tv.) We also use the notation T 1 ă T to denote that T has a non-fringe subtree of shape T 1 at its root. Figure 2 shows some examples of fringe and non-fringe subtrees. fringe subtrees of T T non-fringe subtrees of T Figure 2: Examples of fringe and non-fringe subtrees. Let ξ be a non-negative integer-valued random variable. The Galton-Watson tree T gw with offspring distribution ξ is the random tree generated by starting from the root and independently giving each node a random number of children, where the numbers gw gw of children are all distributed as ξ. The conditional Galton-Watson tree Tn is T restricted to the event |T gw| “ n, i.e., T gw has n nodes. The comprehensive survey by Janson [21] describes the history and the basic properties of these trees. In the study of conditional Galton-Watson trees, the following is usually assumed throughout the paper: gw Condition A. Let Tn be a conditional Galton-Watson tree of size n with offspring dis- tribution ξ, such that Eξ “ 1 and 0 ă σ2 :“ Var pξq ă 8. Let T gw be the corresponding unconditional Galton-Watson tree. 2 We summarize notations: ¨ T | the set of all rooted, ordered and unlabeled trees (plane trees) ¨ T | a tree in T ¨ Tv | a fringe subtree of T rooted at node v P T ¨ ξ | a non-negative integer-valued random variable with Eξ “ 1 and 0 ă σ2 :“ Var pξq ă 8 ¨ h | the span of ξ, i.e., gcdti ¥ 1 : pi ¡ 0u ¨ T gw | an unconditional Galton-Watson tree with offspring distribution ξ gw gw gw ¨ Tn | T given that |T | “ n gw gw gw ¨ Tn;v | a fringe subtree of Tn rooted at node v P Tn gw gw gw ¨ Tn;˚ | a fringe subtree of Tn rooted at a uniform random node of Tn ¨ Tn | a sequence of trees ¨ Sn | the set of all trees of size n ¨ S | a set of trees ` gw ¨ S¤n | the set tT P T : |T | ¤ n; P tT “ T u ¡ 0u ¨ An | a sequence of sets of trees gw gw ¨ NS pTn q | the number of fringe subtrees of Tn that belong to S ¨ πpSq | P tT gw P Su nf gw gw ¨ NT pTn q | the number of non-fringe subtrees of Tn of shape T ¨ πnf pT q | P tT ă T gwu, the probability that T gw has a non-fringe subtree T at its root gw If p1 “ 0, then there exist positive integers n such that P t|T | “ nu “ 0. For such gw gw n, Tn is not well-defined. But it is easy to show that P t|T | “ nu ¡ 0 for all n ¥ n0 with n ´ 1 ” 0 pmod hq, where h is span of ξ and n0 depends only on ξ (see [21, cor. gw gw 15.6]). Therefore, in this paper, for all asymptotic results about T and Tn , the limits are always taken along the subsequence with n ´ 1 ” 0 pmod hq. Extending a result by Aldous [1], Janson [21, thm. 7.12] proved the following theorem: gw gw Theorem 1. Assume Condition A. The conditional distribution LpTn;˚ |Tn q converges in probability to LpT gwq. In other words, for all T P T, as n Ñ 8, gw N pT q p T n “ P T gw “ T |T gw Ñ P tT gw “ T u : (1) n n;˚ n ( 3 Later Janson strengthened the above result, proving the asymptotic normality of gw gw NT pTn q by studying additive functionals on Tn [22]. gw gw A natural generalization of NT pTn q is to consider fringe subtree counts NTn pTn q where Tn P T is a sequence of trees instead of a fixed tree T . Let Popλq denote a Poisson random variable with mean λ. We have: gw Theorem 2. Assume Condition A. Let πpT q :“ P tT “ T u and let kn Ñ 8; kn “ opnq. Then gw lim sup dTV pNT pTn q; PopnπpT qqq “ 0; (2) nÑ8 T :|T |“kn where dTV p ¨ ; ¨ q denotes the total variation distance. Therefore, letting Tn be a sequence of trees with |Tn| “ kn, we have as n Ñ 8: gw (i) If nπpTnq Ñ 0, then NTn pTn q “ 0 whp. gw d (ii) If nπpTnq Ñ µ P p0; 8q, then NTn pTn q Ñ Popµq. (iii) If nπpTnq Ñ 8, then N pT gwq ´ nπpT q Tn n n Ñd Np0; 1q; nπpTnq a d where Np0; 1q denotes the standard normal distribution, and Ñ denotes conver- gence in distribution. In Theorem 2, (i){(iii) follow directly from (2) by the following lemma, whose simple proof we omit: Lemma 1. Let Xn be a sequence of random variables. Let µn be a sequence of non- negative real numbers. Assume that dTV pXn; Popµnqq Ñ 0 as n Ñ 8. We have: (i) If µn Ñ 0, then Xn “ 0 whp. d (ii) If µn Ñ µ P p0; 8q, then Xn Ñ Popµq. ? d (iii) If µn Ñ 8, then pXn ´ µnq{ µn Ñ Np0; 1q: Theorem 2 can be generalized as follows: Theorem 3. Assume Condition A. Let Skn be the set of all trees of size kn, where gw gw kn Ñ 8 and kn “ opnq. For S Ď Skn , let πpSq :“ P tT P Su and NS pTn q :“ gw vPT gw Tn;v P S . Then n J K ř gw lim sup dTV pNS pTn q; PopnπpSqqq “ 0: nÑ8 SĎSkn Therefore, letting An be a sequence of sets of trees with An Ď Skn , we have: 4 gw (i) If nπpAnq Ñ 0, then NAn pTn q “ 0 whp. gw d (ii) If nπpAnq Ñ µ P p0; 8q, then NAn pTn q Ñ Popµq. (iii) If nπpAnq Ñ 8, then N pT gwq ´ nπpA q An n n Ñd Np0; 1q: nπpAnq a The proof of Theorem 2 is given in Section 3. It uses many ingredients from previous results on fringe subtrees, especially from Janson [22]. (In particular, Lemma 6.2 of gw [22] makes the computation of the variance of NSn pTn q quite easy, which is crucial for the proof.) The key step of the proof is based on subtree switching. It permits the coupling of two conditional Galton-Watson trees. Then we can apply the exchangeable pair method by Chatterjee et al. [5], which is an extension of Stein's method [29], to study the convergence of total variation distance. This approach can easily be modified to prove Theorem 3, whose steps we sketch at the end of Section 3. Binary search trees and recursive trees are also well-studied random tree models (see Drmota [11]). Many authors have found results similar to Theorem 2 for these two types of trees, see, e.g., [14, 18, 8, 9, 17].
Load more

Recommended publications
  • PRECISION INTERFEROMETER 012-07137B Precision Interferometer
    Includes 012-07137B Teacher's Notes Instruction Manual and and Typical Experiment Results Experiment Guide for the PASCO scientific Models OS-9255A thru OS-9258A PRECISION INTERFEROMETER 012-07137B Precision Interferometer Table of Contents Section Page Copyright, Warranty, and Equipment Return .................................................ii-iii Introduction ...................................................................................................... 1 Equipment ........................................................................................................ 2 Theory of Operation ......................................................................................... 4 Michelson Twyman-Green Fabry-Perot Setup and Operation ......................................................................................... 6 Tips on Using the Interferometer...................................................................... 9 Sources of Error Troubleshooting Experiments Experiment 1: Introduction to Interferometry ..................................... 11 Experiment 2: The Index of Refraction of Air ................................... 13 Experiment 3: The Index of Refraction of Glass ................................ 15 Suggestions for Additional Experiments ......................................................... 17 Maintenance .................................................................................................... 18 Teacher's Guide ..........................................................................................
    [Show full text]
  • Accreditation Standards and School Personnel Records
    Joy Hofmeister State Superintendent of Public Instruction Oklahoma State Department of Education School Personnel Records Reporting Information Accreditation Standards and School Personnel Records Purpose of the School Personnel Records Section The School Personnel Records (SPR) office at the Oklahoma State Department of Education (OSDE) is responsible for maintaining the annual certified and support personnel reports, administrators’ salary and benefit reports, superintendents’ contracts, and approved salary schedules for each school district. Additionally, the office maintains the historical employment data for all certified and support school employees. The office staff is responsible for reviewing and approving work experience for school employees and updating each teacher’s record for all approved teaching experience. The SPR office reviews the salaries reported by the school districts on each of its teachers to ensure that teachers are paid in accordance with state law. Notices are sent to the school district identifying those teachers who have been underpaid so corrective actions can be taken before a penalty in State Aid is assessed. Additionally, noncertified teachers are monitored and this information is reported to the appropriate persons so corrective actions can be taken. The SPR office reviews complaints of salary reduction without proportionate reduction in duties per 70 O.S. § 18-114.9 and OAC 210:25-3-4(i), and makes recommendations to the State Board of Education for corrective actions. The office also responds to requests for information that is subject to the Oklahoma Open Records Act for any of the above information. Welcome and Certify Screen The Welcome screen’s main function is for the superintendent to CERTIFY the Certified Personnel Report, Support Personnel Report, Online School Directory and Local Salary Schedule.
    [Show full text]
  • Brazil: Background and U.S. Relations
    Brazil: Background and U.S. Relations Updated July 6, 2020 Congressional Research Service https://crsreports.congress.gov R46236 SUMMARY R46236 Brazil: Background and U.S. Relations July 6, 2020 Occupying almost half of South America, Brazil is the fifth-largest and fifth-most-populous country in the world. Given its size and tremendous natural resources, Brazil has long had the Peter J. Meyer potential to become a world power and periodically has been the focal point of U.S. policy in Specialist in Latin Latin America. Brazil’s rise to prominence has been hindered, however, by uneven economic American Affairs performance and political instability. After a period of strong economic growth and increased international influence during the first decade of the 21st century, Brazil has struggled with a series of domestic crises in recent years. Since 2014, the country has experienced a deep recession, record-high homicide rate, and massive corruption scandal. Those combined crises contributed to the controversial impeachment and removal from office of President Dilma Rousseff (2011-2016). They also discredited much of Brazil’s political class, paving the way for right-wing populist Jair Bolsonaro to win the presidency in October 2018. Since taking office in January 2019, President Jair Bolsonaro has begun to implement economic and regulatory reforms favored by international investors and Brazilian businesses and has proposed hard-line security policies intended to reduce crime and violence. Rather than building a broad-based coalition to advance his agenda, however, Bolsonaro has sought to keep the electorate polarized and his political base mobilized by taking socially conservative stands on cultural issues and verbally attacking perceived enemies, such as the press, nongovernmental organizations, and other branches of government.
    [Show full text]
  • Occasional Papers of the Museum of Zoology University of Michigan Annarbor, Miciiigan
    OCCASIONAL PAPERS OF THE MUSEUM OF ZOOLOGY UNIVERSITY OF MICHIGAN ANNARBOR, MICIIIGAN THE SPHAERODACTYLUS (SAURIA: GEKKONIDAE) OF MIDDLE AMERICA INTRODUCTION Splzaerodactylus is one of the most speciose genera of gekkonid lizards. It is confined to the Neotropics, and the majority of its divers- ity is found in the West Indies where approximately 69 species, and an additional 74 subspecies, have been well-documented (King, 1962; Schwartz, 1964, 1966, 1968, 1977; Schwartz and Garrido, 1981; Schwartz and Graham, 1980; Schwartz and Thomas, 1964, 1975, 1983; Schwartz, Thomas, and Ober, 1978; Thomas, 1964, 1975; Thomas and Schwartz, 1966a,b). The mainland radiation was poorly understood until 1982 when Harris published his revision of South American sphaerodactyls. No comprehensive study has yet been at- tempted for Middle American forms, and it remains the last area of taxonomic confusion in the genus. The number of taxa currently recognized in Middle America is not great (10 species according to Peters and Donoso-Barros [1970], Schwartz [1973], and Smith and Taylor [1950b, 19661); however, their geographic distribution and variation, and status as species or subspecies remain to be con- vincingly demonstrated. The Middle American sphaerodactyl fauna appears to be divisible into two geographical-historical components. Most of the taxa may be thought of as belonging to an endemic group because the sister taxon *Division of Amphibians and Reptiles, Museum of Zoology, The University of Michi- gan, Ann Arbor, Michigan 48109-1079 U.S.A. 2 Harris and Kluge Orc. P~I~P):) of each species also exhibits a mainland distribution. Only two, S. arg-us Gosse (1850) and S.
    [Show full text]
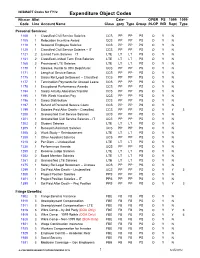
  • Expenditure Object Codes Wismart Allot Cate- OPER PS 1099 1099 Code Line Account Name Class Gory Type Group /N-OP IND Rept Type
    WiSMART Codes for FY12 Expenditure Object Codes Wismart Allot Cate- OPER PS 1099 1099 Code Line Account Name Class gory Type Group /N-OP IND Rept Type Personal Services: 1100 1 Classified Civil Service Salaries CCS PP PP PS O Y N 1105 1 Relocation Incentive Award CCS PP PP PS O Y N 1110 1 Seasonal Employee Salaries CCS PP PP PS O Y N 1120 1 Classified Civil Service Salaries – IT CCS PP PP PS O Y N 1121 2 Limited Term Salaries – IT LTE LT LT PS O Y N 1161 2 Classified Limited Term Emp Salaries LTE LT LT PS O Y N 1168 2 Provisional LTE Salaries LTE LT LT PS O Y N 1170 1 Salaries, Reimb to Othr Dept/Munic CCS PP PP PS O Y N 1171 1 Length of Service Bonus CCS PP PP PS O Y N 1175 1 Salary Rel Legal Settlement – Classified CCS PP PP PS O Y N 1177 1 Termination Payments for Unused Leave CCS PP PP PS O Y N 1179 1 Exceptional Performance Awards CCS PP PP PS O Y N 1194 1 Salary Activity Allocation/Transfer CCS PP PP PS O Y N 1195 1 Fifth Week Vacation Pay CCS PP PP PS O Y N 1196 1 Salary Distribution CCS PP PP PS O Y N 1197 1 Refund of Personal Service Costs CCS PP PP PS O Y N 1199 1 Salaries Paid After Death – Classified CCS PP PP PS O Y Y 3 1200 1 Unclassified Civil Service Salaries UCS PP PP PS O Y N 1201 1 Unclassified Civil Service Salaries – IT UCS PP PP PS O Y N 1202 2 Student Salaries LTE LT LT PS O Y N 1205 1 Research Assistant Salaries UCS PP PP PS O Y N 1208 2 Work Study – Reimbusement LTE LT LT PS O Y N 1209 1 Other Assistant Salaries UCS PP PP PS O Y N 1210 2 Per Diem – Unclassified LTE LT LT PS O Y N 1230 1 Performance Awards UCS
    [Show full text]
  • The Science of “Fringe”
    THE SCIENCE OF “FRINGE” EXPLORING: METEORITES A SCIENCE OLYMPIAD THEMED LESSON PLAN EPISODE 315: Os Overview: Students will learn about meteorites and ways of finding them. Grade Level: 9-12 Episode Summary: The Fringe Team investigates a deceased thief who is found floating in mid-air. Walter and the team try to determine what is making his body float and why he was trying to steal Osmium, the densest element. Meanwhile, the scientist behind the invention that allowed the thief to float works on recruiting additional test subjects to help him refine his invention. He enlists their help in getting the raw materials he needs, some of which are only available from meteorites. Related Science Olympiad Event: Astronomy - Teams will demonstrate an understanding of the basic concepts of math and physics relating to galaxies. Learning Objectives: Students will understand the following: • Meteorites are objects from space that survive the trip through the atmosphere and impact with the ground. • Meteorites are classified into 3 types: rocky, iron, and stony-iron. • Most meteorites are small and do not create a crater, but can be identified by their unique characteristics compared to terrestrial rocks. © FOX/Science Olympiad, Inc./FringeTM/Warner Brothers Entertainment, Inc. All rights reserved. 1 Episode Scenes of Relevance: • The Fringe Team discussing Lutetium and where it can be found (30:12 ‘mixed with’ – 31:02 ‘call Broyles’) • The thieves examining meteorites (33:04 ‘almost done’ – 33:35 ‘need your help’) Online Resources: • Fringe “Os” full episode: http://www.Fox.com/watch/Fringe • Science Olympiad Astronomy event: http://soinc.org/astronomy_c • NASA Meteors and Meteorites: http://solarsystem.nasa.gov/planets/profile.cfm?Object=Meteors • Meteorite.org: http://meteorite.org/ Procedures: 1.
    [Show full text]
  • Maintaining Viability of Brown Bears Along the Southern Fringe of Their Distribution
    MAINTAININGVIABILITY OF BROWNBEARS ALONGTHE SOUTHERNFRINGE OF THEIRDISTRIBUTION BRUCEN. McLELLAN,British Columbia Ministry of Forests Research Branch,RPO #3, Box 9158, Revelstoke,BC VOE3KO, Canada, email: [email protected] Abstract: In North America, threatenedbrown bears (Ursusarctos) and brown bear recovery are usually viewed as United States' issues. Most of the southern fringe of brown bear distribution,however, is in Canada;approximately 3,050 km of occupied-unoccupied fringe are in British Columbiaand 1,570 km are in Albertacompared to 1,700 km in the lower 48 states. The distributionof brown bears in southernCanada has been poorly documentedand publicized but, in additionto their inherentvalue, these bears are critical to the viability of brown bears in the U.S. In this paperI presenta British Columbianview of brown bears along their southernfringe and humaninfluences relatedto industry,settlement, hunting, and fragmentation. I also describe scales of land-use planningin British Columbiaand the consensus process on which they are developed. Even with well intendedplans, maintainingbrown bear numbersand distributionis an increasinglydifficult challenge because human populationsare rapidly growing in and adjacentto brown bear range. Given the increase in people, humanbehavior will have to change to accommodatebears, and changing human behavior will involve reducing individualrights and privileges that are enjoyed in western North America. Ursus 10:607-611 Key words: Alberta, British Columbia, brown bear, fragmentation,hunting, industry,land-use planning, settlement, Ursus arctos. Although details were poorly recordedand what was tied States. Their distributionin 4 separate areas of once known has died with memories, the general de- the lower 48 states has been well documented by the mise of the brown bear (Ursusarctos) in North America U.S.
    [Show full text]
  • Transmedia Storytelling and User-Generated Content
    GUERRERO-PICO, M. y SCOLARI, C.A. Transmedia storytelling and user-generated content CUADERNOS.INFO Nº 38 ISSN 0719-3661 Versión electrónica: ISSN 0719-367x http://www.cuadernos.info doi: 10.7764/cdi.38.760 Received: 04-15-2015 / Accepted: 03-23-2016 Transmedia storytelling and user-generated content: A case study on crossovers Narrativas transmedia y contenidos generados por los usuarios: el caso de los crossovers Narrativas transmídia e conteúdos gerados por usuários: o caso dos crossovers MAR GUERRERO-PICO, Departamento de Comunicación, Universitat Pompeu Fabra, Barcelona, España [[email protected]] CARLOS A. SCOLARI, Departamento de Comunicación, Universitat Pompeu Fabra, Barcelona, España [[email protected]] ABSTRACT RESUMEN RESUMO The aim of this article is to analyze a El objetivo de este artículo es analizar un O objetivo deste artigo é analisar um tipo special type of textuality: crossovers. tipo especial de textualidad: los crossovers. especial de textualidade: os crossovers. A The analy¬sis focuses on user-generated El análisis se focalizará en los contenidos análise se centra nos conteúdos gerados content in the transmedia storytelling generados por los usuarios de las narrati- pelos usuários de narrativas transmídia. context. The study follows a series of vas transmedia. Para ello, se toman como Para isso, 25 produções derivadas das 25 productions derivative of ABC’s Lost caso 25 producciones derivadas de dos se- séries de televisão Lost (ABC, 2004- (2004- 2010) and FOX’s Fringe (2008- ries televisivas: Lost (ABC, 2004-2010) y 2010) e Fringe (FOX, 2008-2013) são 2013). After describing the scenario where Fringe (FOX, 2008-2013).
    [Show full text]
  • W:\Doc\Csm\Kmpa\Kmpa
    OFFICIAL STATEMENT NEW ISSUE RATINGS: Moody's: "Aa3" (negative outlook) - AGM (as defined herein), Underlying: "A3" BOOK ENTRY Standard & Poor's: "AAA" (negative outlook) - AGM (as defined herein), Underlying: "A-" See "RATINGS" herein. In the opinion of Bond Counsel, based upon laws, regulations, rulings and decisions, and assuming continuing compliance with certain covenants made by the Corporation, interest on the Series 2010A Bonds is excludable from gross income for federal income tax purposes and is not an item of tax preference for purposes of the federal alternative minimum tax imposed on individuals and corporations, upon the conditions and subject to the limitations set forth herein under the caption "TAX EXEMPTION." Receipt of interest on the Series 2010A Bonds may result in other federal income tax consequences to certain holders of the Series 2010A Bonds. In the opinion of Bond Counsel, interest on the Series 2010A Bonds, the Series 2010B Bonds and the Series 2010C Bonds is also exempt from income tax by the Commonwealth of Kentucky, and the Series 2010A Bonds, the Series 2010B Bonds and the Series 2010C Bonds are exempt from ad valorem taxation by the Commonwealth of Kentucky and any of its political subdivisions. KENTUCKY MUNICIPAL POWER AGENCY $53,600,000 $122,405,000 Tax-Exempt Power System Revenue Bonds Taxable (Build America Bonds - Direct Pay) (Prairie State Project), Series 2010A Power System Revenue Bonds (Prairie State Project), Series 2010B $7,725,000 Taxable Power System Revenue Bonds (Prairie State Project), Series 2010C Dated Date: Date of Issuance Due: As set forth herein on the inside front cover The Bonds will bear interest payable semiannually on March 1 and September 1 of each year (each an "Interest Payment Date"), commencing September 1, 2010, as determined in accordance with the Trust Indenture dated as of April 1, 2010 (the "Indenture"), between the Kentucky Municipal Power Agency ("KMPA") and U.S.
    [Show full text]
  • Accommodating Oversize/Overweight Vehicles at Roundabouts
    Report No. K-TRAN: KSU-10-1 ▪ FINAL REPORT▪ January 2013 Accommodating Oversize/Overweight Vehicles at Roundabouts Eugene R. Russell, Sr., P.E., Ph.D. Professor Emeritus E. Dean Landman, P.E. Adjunct Professor Ranjit Godavarthy GRA, Ph.D. Candidate Kansas State University Transportation Center A cooperative transportation research program between Kansas Department of Transportation, Kansas State University Transportation Center, and The University of Kansas This page intentionally left blank. i 1 Report No. 2 Government Accession No. 3 Recipient Catalog No. K-TRAN: KSU-10-1 4 Title and Subtitle 5 Report Date Accommodating Oversize/Overweight Vehicles at Roundabouts January 2013 6 Performing Organization Code 7 Author(s) 8 Performing Organization Report No. Eugene R. Russell, Sr., P.E., Ph.D.; E. Dean Landman, P.E., Ranjit Godavarthy 9 Performing Organization Name and Address 10 Work Unit No. (TRAIS) Department of Civil Engineering Kansas State University Transportation Center 11 Contract or Grant No. 2118 Fiedler Hall C1860 Manhattan, Kansas 66506 C1859 12 Sponsoring Agency Name and Address 13 Type of Report and Period Covered Kansas Department of Transportation Final Report Bureau of Materials and Research January 2010–August 2012 700 SW Harrison Street 14 Sponsoring Agency Code Topeka, Kansas 66603-3745 TPF-5(220) RE-0520-01 15 Supplementary Notes For more information write to address in block 9. 16 Abstract Safety and traffic operational benefits of roundabouts for the typical vehicle fleet (automobiles and small trucks) have been well documented. Although roundabouts have been in widespread use in other countries for many years, their general use in the United States began only in the recent past.
    [Show full text]
  • Chapter Sixteen: Rodents and Other Vertebrate Invaders in the United States
    University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln USDA National Wildlife Research Center - Staff U.S. Department of Agriculture: Animal and Publications Plant Health Inspection Service 2011 Chapter sixteen: Rodents and other vertebrate invaders in the United States Michael W. Fall National Wildlife Research Center, U. S. Department of Agriculture, [email protected] Michael L. Avery USDA/APHIS/WS National Wildlife Research Center, [email protected] Tyler A. Campbell National Wildlife Research Center, [email protected] Peter J. Egan National Wildlife Research Center, U. S. Department of Agriculture Richard M. Engeman USDA-APHIS-Wildlife Services, [email protected] See next page for additional authors Follow this and additional works at: https://digitalcommons.unl.edu/icwdm_usdanwrc Fall, Michael W.; Avery, Michael L.; Campbell, Tyler A.; Egan, Peter J.; Engeman, Richard M.; Pimentel, David; Pitt, William C.; Shwiff, Stephanie A.; and Witmer, Gary W., "Chapter sixteen: Rodents and other vertebrate invaders in the United States" (2011). USDA National Wildlife Research Center - Staff Publications. 1308. https://digitalcommons.unl.edu/icwdm_usdanwrc/1308 This Article is brought to you for free and open access by the U.S. Department of Agriculture: Animal and Plant Health Inspection Service at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in USDA National Wildlife Research Center - Staff Publications by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. Authors Michael W. Fall, Michael L. Avery, Tyler A. Campbell, Peter J. Egan, Richard M. Engeman, David Pimentel, William C. Pitt, Stephanie A. Shwiff, and Gary W. Witmer This article is available at DigitalCommons@University of Nebraska - Lincoln: https://digitalcommons.unl.edu/ icwdm_usdanwrc/1308 RodtnlS and otIIIf ¥M.ftnle InwderIIn the UnIIed SUt",,- 2011.
    [Show full text]
  • Quality Jobs Program Application & Guidelines
    Quality Jobs Program Application & Guidelines Published January 2021 OKLAHOMA BUSINESS INCENTIVES AND TAX GUIDE FOR FISCAL YEAR 2020 Welcome to the 2020 Oklahoma Business Incentives and Tax Information Guide. The rules, legislation and appropriations related to taxes and incentives are very dynamic, and as changes occur, this Tax Guide will be updated. We encourage you to refer often to this on-line tax guide, as well as the various included hyperlinks, to get the most current information. TABLE OF CONTENTS CASH PAYMENT INCENTIVES ......................................................................................................................................5 THE OKLAHOMA QUALITY JOBS PROGRAM ...........................................................................................................5 VETERANS INCLUSION ............................................................................................................................................5 CLAW BACK PROVISION ..........................................................................................................................................5 PAYROLL THRESHOLD REQUIREMENT ....................................................................................................................5 QUALITY JOBS PROGRAM QUALIFYING INDUSTRIES ..............................................................................................6 SMALL EMPLOYER QUALITY JOBS PROGRAM ........................................................................................................7
    [Show full text]