12 Nov 2013 Litclglxe.Wt H Rsneo Uemsiebla Supermassive of Presence the with Galaxies
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

VEGAS: a VST Early-Type Galaxy Survey. the Faint Substructures of NGC 4472 Stellar Halo
VEGAS: A VST Early-type GAlaxy Survey. The faint substructures of NGC 4472 stellar halo. MARILENA SPAVONE ON THE BEHALF OF THE VEGAS TEAM: M. CAPACCIOLI, M. CANTIELLO, A. GRADO, E. IODICE, F. LA BARBERA, N.R. NAPOLITANO, C. TORTORA, L. LIMATOLA, M. PAOLILLO, T. PUZIA, R. PELETIER, A.J. ROMANOWSKY, D. FORBES, G. RAIMONDO OUTLINE The VST VEGAS survey Science aims Results on NGC 4472 field Conclusions Future plans MARILENA SPAVONE STELLAR HALOS 2015 ESO-GARCHING, 23-27 FEBRUARY THE VEGAS SURVEY Multiband u, g, r, i survey of ~ 110 galaxies with vrad < 4000 km/s in all environments (field to clusters). An example Obj. name Morph. type u g r i IC 1459 E3 5630 1850 1700 NGC 1399 E1 8100 5320 2700 NGC 3115 S0 14800 8675 6030 Observations to date (to P94) g-BAND ~ 16% i-BAND ~ 19% r-BAND ~ 3% + FORNAX u-BAND ~ 1% MARILENA SPAVONE STELLAR HALOS 2015 ESO-GARCHING, 23-27 FEBRUARY THE VEGAS SURVEY Multiband u, g, r, i survey of ~ 110 galaxies with vrad < 4000 km/s in all environments (field to clusters). OT ~ 350 h @ vst over 5 years Expected SB limits: 27.5 g, 2 27.0 r and 26.2 i mag/arcsec . g band expected SB limit MARILENA SPAVONE STELLAR HALOS 2015 ESO-GARCHING, 23-27 FEBRUARY THE VEGAS SURVEY Multiband u, g, r, i survey of ~ 110 galaxies with vrad < 4000 km/s in all environments (field to clusters). ~ 350 h @ vst over 5 years Expected SB limits: 27.5 g, 27.0 r and 26.2 i mag/arcsec2. -

The Globular Cluster System of NGC 1316 (Fornax A) During a Merger Event
Astronomy & Astrophysics manuscript no. (will be inserted by hand later) The Globular Cluster System of NGC 1316 (Fornax A) M. G´omez1,2, T. Richtler3, L. Infante1, and G. Drenkhahn4 1 Departamento de Astronom´ıa y Astrof´ısica, P. Universidad Cat´olica de Chile. Casilla 306, Santiago, Chile e-mail: [email protected],[email protected] 2 Sternwarte der Universit¨at Bonn, Auf dem H¨ugel 71, D-53121 Bonn, Germany 3 Departamento de F´ısica, Universidad de Concepci´on. Casilla 4009, Concepci´on, Chile e-mail: [email protected] 4 Max-Planck-Institut f¨ur Astrophysik, Postfach 1317, D-85741 Garching bei M¨unchen, Germany e-mail: [email protected] Received ... / Accepted ... Abstract. We have studied the Globular Cluster System of the merger galaxy NGC 1316 in Fornax, using CCD BVI photometry. A clear bimodality is not detected from the broadband colours. However, dividing the sample into red (presumably metal-rich) and blue (metal-poor) subpopulations at B − I = 1.75, we find that they follow strikingly different angular distributions. The red clusters show a strong correlation with the galaxy elongation, but the blue ones are circularly distributed. No systematic difference is seen in their radial profile and both are equally concentrated. We derive an astonishingly low Specific Frequency for NGC 1316 of only SN = 0.9, which confirms with a larger field a previous finding by Grillmair et al. (1999). Assuming a “normal” SN of ∼ 4 for early-type galaxies, we use stellar population synthesis models to estimate in 2 Gyr the age of this galaxy, if an intermediate-age population were to explain the low SN we observe. -

115 Abell Galaxy Cluster # 373
WINTER Medium-scope challenges 271 # # 115 Abell Galaxy Cluster # 373 Target Type RA Dec. Constellation Magnitude Size Chart AGCS 373 Galaxy cluster 03 38.5 –35 27.0 Fornax – 180 ′ 5.22 Chart 5.22 Abell Galaxy Cluster (South) 373 272 Cosmic Challenge WINTER Nestled in the southeast corner of the dim early winter western suburbs. Deep photographs reveal that NGC constellation Fornax, adjacent to the distinctive triangle 1316 contains many dust clouds and is surrounded by a formed by 6th-magnitude Chi-1 ( 1), Chi-2 ( 2), and complex envelope of faint material, several loops of Chi-3 ( 3) Fornacis, is an attractive cluster of galaxies which appear to engulf a smaller galaxy, NGC 1317, 6 ′ known as Abell Galaxy Cluster – Southern Supplement to the north. Astronomers consider this to be a case of (AGCS) 373. In addition to his research that led to the galactic cannibalism, with the larger NGC 1316 discovery of more than 80 new planetary nebulae in the devouring its smaller companion. The merger is further 1950s, George Abell also examined the overall structure signaled by strong radio emissions being telegraphed of the universe. He did so by studying and cataloging from the scene. 2,712 galaxy clusters that had been captured on the In my 8-inch reflector, NGC 1316 appears as a then-new National Geographic Society–Palomar bright, slightly oval disk with a distinctly brighter Observatory Sky Survey taken with the 48-inch Samuel nucleus. NGC 1317, about 12th magnitude and 2 ′ Oschin Schmidt camera at Palomar Observatory. In across, is visible in a 6-inch scope, although averted 1958, he published the results of his study as a paper vision may be needed to pick it out. -

Revealing Hidden Substructures in the $ M {BH} $-$\Sigma $ Diagram
Draft version November 14, 2019 A Typeset using L TEX twocolumn style in AASTeX63 Revealing Hidden Substructures in the MBH –σ Diagram, and Refining the Bend in the L–σ Relation Nandini Sahu,1,2 Alister W. Graham2 And Benjamin L. Davis2 — 1OzGrav-Swinburne, Centre for Astrophysics and Supercomputing, Swinburne University of Technology, Hawthorn, VIC 3122, Australia 2Centre for Astrophysics and Supercomputing, Swinburne University of Technology, Hawthorn, VIC 3122, Australia (Accepted 2019 October 22, by The Astrophysical Journal) ABSTRACT Using 145 early- and late-type galaxies (ETGs and LTGs) with directly-measured super-massive black hole masses, MBH , we build upon our previous discoveries that: (i) LTGs, most of which have been 2.16±0.32 alleged to contain a pseudobulge, follow the relation MBH ∝ M∗,sph ; and (ii) the ETG relation 1.27±0.07 1.9±0.2 MBH ∝ M∗,sph is an artifact of ETGs with/without disks following parallel MBH ∝ M∗,sph relations which are offset by an order of magnitude in the MBH -direction. Here, we searched for substructure in the MBH –(central velocity dispersion, σ) diagram using our recently published, multi- component, galaxy decompositions; investigating divisions based on the presence of a depleted stellar core (major dry-merger), a disk (minor wet/dry-merger, gas accretion), or a bar (evolved unstable 5.75±0.34 disk). The S´ersic and core-S´ersic galaxies define two distinct relations: MBH ∝ σ and MBH ∝ 8.64±1.10 σ , with ∆rms|BH = 0.55 and 0.46 dex, respectively. We also report on the consistency with the slopes and bends in the galaxy luminosity (L)–σ relation due to S´ersic and core-S´ersic ETGs, and LTGs which all have S´ersic light-profiles. -

Bimodality in Low-Luminosity E and S0 Galaxies
Mon. Not. R. Astron. Soc. 387, 331–343 (2008) doi:10.1111/j.1365-2966.2008.13235.x Bimodality in low-luminosity E and S0 galaxies A. E. Sansom⋆ and M. S. Northeast Centre for Astrophysics, University of Central Lancashire, Preston, Lancs PR1 HE Accepted 2008 March 17. Received 2008 February 14; in original form 2007 November 26 ABSTRACT Stellar population characteristics are presented for a sample of low-luminosity early-type galaxies (LLEs) in order to compare them with their more luminous counterparts. Long-slit spectra of a sample of 10 LLEs were taken with the ESO New Technology Telescope, selected for their low luminosities. Line strengths were measured on the Lick standard system. Lick indices for these LLEs were correlated with velocity dispersion (σ), alongside published data for a variety of Hubble types. The LLEs were found to fall below an extrapolation of the correlation for luminous ellipticals and were consistent with the locations of spiral bulges in plots of line strengths versus σ. Luminosity weighted average ages, metallicities and abundance ratios were estimated from χ 2 fitting of 19 Lick indices to predictions from simple stellar population models. The LLEs appear younger than luminous ellipticals and of comparable ages to spiral bulges. These LLEs show a bimodal metallicity distribution, consisting of a low- metallicity group (possibly misclassified dwarf spheroidal galaxies) and a high-metallicity group (similar to spiral bulges). Finally, they have low α-element to iron peak abundance ratios indicative of slow, extended star formation. Key words: galaxies: abundances – galaxies: elliptical and lenticular, cD – galaxies: evolution. -

Extended Stellar Kinematics of Elliptical Galaxies in the Fornax Cluster?,??
ASTRONOMY & ASTROPHYSICS DECEMBER II 1998, PAGE 325 SUPPLEMENT SERIES Astron. Astrophys. Suppl. Ser. 133, 325–336 (1998) Extended stellar kinematics of elliptical galaxies in the Fornax cluster?,?? A.W. Graham1, M.M. Colless1, G. Busarello2, S. Zaggia2, and G. Longo2 1 Mount Stromlo and Siding Spring Observatories, Australian National University, PMB Weston Creek PO, ACT 2611, Australia 2 Osservatorio Astronomico di Capodimonte, via Moiariello 16, I-80131 Napoli, Italy Received February 4; accepted June 17, 1998 Abstract. We present extended stellar kinematics for 1. Introduction a sample of elliptical galaxies in the Fornax cluster. Out of the 13 galaxies presented here, five (FCC 119, The scaling relations between some global properties of FCC 136, NGC 1373, NGC 1428, FCC 335) have no pre- ellipticals (Es), known as the “Fundamental Plane” (FP; viously published kinematical data. Major-axis velocity Dressler et al. 1987; Djorgovski & Davis 1987), is clearly a dispersion profiles (VDPs) and rotation curves (RCs) are manifestation of a great “regularity” in the properties of given for 12 of the galaxies. A major feature of this data Es. Although a proof of its “universality” is still lacking, is the spatial extension: for 8 galaxies the data extends the FP has been widely applied to various problems: from the study of peculiar motions (Lynden-Bell et al. 1988; beyond 1 Re, and for 5 it extends beyond 2 Re. Compared to the previously available data, this corresponds to an Jørgensen et al. 1996), to the study of the evolution of increase in spatial coverage by a factor from 1 to 5. -

Central Stellar Mass Deficits in the Bulges of Local Lenticular Galaxies, and the Connection with Compact Z~ 1.5 Galaxies
Draft version August 21, 2018 A Preprint typeset using LTEX style emulateapj v. 5/2/11 CENTRAL STELLAR MASS DEFICITS IN THE BULGES OF LOCAL LENTICULAR GALAXIES, AND THE CONNECTION WITH COMPACT Z ∼ 1.5 GALAXIES Bililign T. Dullo1, Alister W. Graham1 1 Centre for Astrophysics and Supercomputing, Swinburne University of Technology, Hawthorn, Victoria 3122, Australia; [email protected] Draft version August 21, 2018 ABSTRACT We have used the full radial extent of images from the Hubble Space Telescope’s Advanced Camera for Surveys and Wide Field Planetary Camera 2 to extract surface brightness profiles from a sample of six, local lenticular galaxy candidates. We have modelled these profiles using a core-S´ersic bulge plus an exponential disk model. Our lenticular disk galaxies with bulge magnitudes MV . −21.30 mag have central stellar deficits, suggesting that these bulges may have formed from ‘dry’ merger events involving supermassive black holes while their surrounding disk was subsequently built up, perhaps via cold gas accretion scenarios. The central stellar mass deficits Mdef are roughly 0.5 to 2 MBH (black hole mass), rather than ∼10 to 20 MBH as claimed from some past studies, which is in accord with core-S´ersic model mass deficit measurements in elliptical galaxies. Furthermore, these 11 bulges have S´ersic indices n ∼ 3, half light radii Re < 2 kpc and masses > 10 M⊙, and therefore appear to be descendants of the compact galaxies reported at z ∼ 1.5 to 2. Past studies which have searched for these local counterparts by using single-component galaxy models to provide the z ∼ 0 size comparisons have over-looked these dense, compact and massive bulges in today’s early-type disk galaxies. -

Ngc Catalogue Ngc Catalogue
NGC CATALOGUE NGC CATALOGUE 1 NGC CATALOGUE Object # Common Name Type Constellation Magnitude RA Dec NGC 1 - Galaxy Pegasus 12.9 00:07:16 27:42:32 NGC 2 - Galaxy Pegasus 14.2 00:07:17 27:40:43 NGC 3 - Galaxy Pisces 13.3 00:07:17 08:18:05 NGC 4 - Galaxy Pisces 15.8 00:07:24 08:22:26 NGC 5 - Galaxy Andromeda 13.3 00:07:49 35:21:46 NGC 6 NGC 20 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 7 - Galaxy Sculptor 13.9 00:08:21 -29:54:59 NGC 8 - Double Star Pegasus - 00:08:45 23:50:19 NGC 9 - Galaxy Pegasus 13.5 00:08:54 23:49:04 NGC 10 - Galaxy Sculptor 12.5 00:08:34 -33:51:28 NGC 11 - Galaxy Andromeda 13.7 00:08:42 37:26:53 NGC 12 - Galaxy Pisces 13.1 00:08:45 04:36:44 NGC 13 - Galaxy Andromeda 13.2 00:08:48 33:25:59 NGC 14 - Galaxy Pegasus 12.1 00:08:46 15:48:57 NGC 15 - Galaxy Pegasus 13.8 00:09:02 21:37:30 NGC 16 - Galaxy Pegasus 12.0 00:09:04 27:43:48 NGC 17 NGC 34 Galaxy Cetus 14.4 00:11:07 -12:06:28 NGC 18 - Double Star Pegasus - 00:09:23 27:43:56 NGC 19 - Galaxy Andromeda 13.3 00:10:41 32:58:58 NGC 20 See NGC 6 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 21 NGC 29 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 22 - Galaxy Pegasus 13.6 00:09:48 27:49:58 NGC 23 - Galaxy Pegasus 12.0 00:09:53 25:55:26 NGC 24 - Galaxy Sculptor 11.6 00:09:56 -24:57:52 NGC 25 - Galaxy Phoenix 13.0 00:09:59 -57:01:13 NGC 26 - Galaxy Pegasus 12.9 00:10:26 25:49:56 NGC 27 - Galaxy Andromeda 13.5 00:10:33 28:59:49 NGC 28 - Galaxy Phoenix 13.8 00:10:25 -56:59:20 NGC 29 See NGC 21 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 30 - Double Star Pegasus - 00:10:51 21:58:39 -

Towards an Understanding of the Globular Cluster Over-Abundance Around the Central -Giant Elliptical NGC 1399 I
Towards an Understanding of the Globular Cluster Over-abundance around the Central -Giant Elliptical NGC 1399 I bIarkus Kissier-Patig '92 Uco/Lick observatory, University of California, Santa Cruz, CA 9,5064. USA Electronic mails: mkissler8ucblick.org Carl J. Grillmajr SIRTF Science Center, Mail Stop 100-22, California Instibute of Technology, Pasadena, CA 9112'5, USA Electronicmail: [email protected] Georges Meylan European Southern Observatory, Iiarl-Schwarzschild-Strasse 2, 0-85748 Garching bei i\.lunchen, Germany Electronic mail: [email protected] Jean P. Brodie UCO/Lick observatory, University of California, Santa Cru:, CA 95064, USA Electronic mail: [email protected] Dante Minniti Lawrence Livermore National Laboratory, Livermore, CA 94550, USA Departamento de Astronomia y Astrofisica, P. Universidad Catdlica, Casilla 104, Santiago 22, Chile Electronic mail: [email protected] Paul Goudfrooij Space Telescope Science Institute, 9700 San ,\[artin Drive, Baltimore, MD 21218. lJSA Electronic mail: [email protected] ABSTRACT We investigate the kinematics of a combined sample of 74 globular clusters around NGCl 1399. Their high velocity dispersion, increasing with radius, supports their associ- ation with the gravitational potentialof the ga.laxy cluster rather than with thatof NGC 'Feodor Lynerl Fellow of the Alexander von Hunlholdt Foundation 2Current address: ESO, Karl-Schwanschild-Str. 2, 85748 Garching, Germany. Email: rnkissler'Qeso.org 3Afiliated with the Astrophysics Division, Space Science Department, European Space Agency, ESTEC, Postbus 299, NL-2200 AG Noordwijk, The Netherlands 1 1399 itself. We find no evidence for rotatiod'fnihe fdIsample, although some indication for rotation in the outer regions. The ,data*donoballow us to detect differences between the kinematics of the blue and red sub-populations of globular clusters. -

The Globular Cluster System of NGC 1316 (Fornax A)
A&A 371, 875–889 (2001) Astronomy DOI: 10.1051/0004-6361:20010457 & c ESO 2001 Astrophysics The globular cluster system of NGC 1316 (Fornax A) M. G´omez1,2,T.Richtler3,L.Infante1, and G. Drenkhahn4 1 Departamento de Astronom´ıa y Astrof´ısica, P. Universidad Cat´olica de Chile, Casilla 306, Santiago, Chile e-mail: [email protected],[email protected] 2 Sternwarte der Universit¨at Bonn, Auf dem H¨ugel 71, 53121 Bonn, Germany 3 Departamento de F´ısica, Universidad de Concepci´on, Casilla 4009, Concepci´on, Chile e-mail: [email protected] 4 Max-Planck-Institut f¨ur Astrophysik, Postfach 1317, 85741 Garching bei M¨unchen, Germany e-mail: [email protected] Received 22 November 2000 / Accepted 22 March 2001 Abstract. We have studied the Globular Cluster System of the merger galaxy NGC 1316 in Fornax, using CCD BV I photometry. A clear bimodality is not detected from the broadband colours. However, dividing the sample into red (presumably metal-rich) and blue (metal-poor) subpopulations at B −I =1.75, we find that they follow strikingly different angular distributions. The red clusters show a strong correlation with the galaxy elongation, but the blue ones are circularly distributed. No systematic difference is seen in their radial profile and both are equally concentrated. We derive an astonishingly low Specific Frequency for NGC 1316 of only SN =0.9, which confirms with a larger field a previous finding by Grillmair et al. (1999). Assuming a “normal” SN of ∼4 for early-type galaxies, we use stellar population synthesis models to estimate in 2 Gyr the age of this galaxy, if an intermediate- age population were to explain the low SN we observe. -

K-BAND SPECTRAL INDICES and an APPLICATION to the FORNAX CLUSTER1 David R
The Astrophysical Journal, 674:194Y208, 2008 February 10 # 2008. The American Astronomical Society. All rights reserved. Printed in U.S.A. A NEW APPROACH TO THE STUDY OF STELLAR POPULATIONS IN EARLY-TYPE GALAXIES: K-BAND SPECTRAL INDICES AND AN APPLICATION TO THE FORNAX CLUSTER1 David R. Silva2, 3 National Optical Astronomy Observatory, 950 North Cherry Avenue, Tucson, AZ 85748; [email protected] Harald Kuntschner Space Telescope European Coordination Facility; [email protected] Karl-Schwarzschild-Strasse 2, D-85748 Garching bei Mu¨nchen, Germany; [email protected] and Mariya Lyubenova European Southern Observatory, Karl-Schwarzschild-Strasse 2, D-85748 Garching bei Mu¨nchen, Germany; [email protected] Received 2007 August 31; accepted 2007 October 18 ABSTRACT The strong spectral features near 2.2 m in early-type galaxies remain relatively unexplored. Yet, they open a tightly focused window on the coolest giant stars in these galaxies—a window that can be used to explore both age and metallicity effects. Here, new measurements of K-band spectral features are presented for 11 early-type galaxies in the nearby Fornax galaxy cluster. Based on these measurements, the following conclusions have been reached: (1) in galaxies with no signatures of a young stellar component, the K-band Na i index is highly correlated with both the optical metallicity indicator [MgFe]0 and the central velocity dispersion ; (2) in the same galaxies, the K-band Fe 1 features saturate in galaxies with > 150 km sÀ , while Na i (and [MgFe]0) continues to increase; (3) [Si/Fe] -
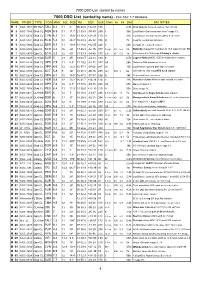
DSO List V2 Current
7000 DSO List (sorted by name) 7000 DSO List (sorted by name) - from SAC 7.7 database NAME OTHER TYPE CON MAG S.B. SIZE RA DEC U2K Class ns bs Dist SAC NOTES M 1 NGC 1952 SN Rem TAU 8.4 11 8' 05 34.5 +22 01 135 6.3k Crab Nebula; filaments;pulsar 16m;3C144 M 2 NGC 7089 Glob CL AQR 6.5 11 11.7' 21 33.5 -00 49 255 II 36k Lord Rosse-Dark area near core;* mags 13... M 3 NGC 5272 Glob CL CVN 6.3 11 18.6' 13 42.2 +28 23 110 VI 31k Lord Rosse-sev dark marks within 5' of center M 4 NGC 6121 Glob CL SCO 5.4 12 26.3' 16 23.6 -26 32 336 IX 7k Look for central bar structure M 5 NGC 5904 Glob CL SER 5.7 11 19.9' 15 18.6 +02 05 244 V 23k st mags 11...;superb cluster M 6 NGC 6405 Opn CL SCO 4.2 10 20' 17 40.3 -32 15 377 III 2 p 80 6.2 2k Butterfly cluster;51 members to 10.5 mag incl var* BM Sco M 7 NGC 6475 Opn CL SCO 3.3 12 80' 17 53.9 -34 48 377 II 2 r 80 5.6 1k 80 members to 10th mag; Ptolemy's cluster M 8 NGC 6523 CL+Neb SGR 5 13 45' 18 03.7 -24 23 339 E 6.5k Lagoon Nebula;NGC 6530 invl;dark lane crosses M 9 NGC 6333 Glob CL OPH 7.9 11 5.5' 17 19.2 -18 31 337 VIII 26k Dark neb B64 prominent to west M 10 NGC 6254 Glob CL OPH 6.6 12 12.2' 16 57.1 -04 06 247 VII 13k Lord Rosse reported dark lane in cluster M 11 NGC 6705 Opn CL SCT 5.8 9 14' 18 51.1 -06 16 295 I 2 r 500 8 6k 500 stars to 14th mag;Wild duck cluster M 12 NGC 6218 Glob CL OPH 6.1 12 14.5' 16 47.2 -01 57 246 IX 18k Somewhat loose structure M 13 NGC 6205 Glob CL HER 5.8 12 23.2' 16 41.7 +36 28 114 V 22k Hercules cluster;Messier said nebula, no stars M 14 NGC 6402 Glob CL OPH 7.6 12 6.7' 17 37.6 -03 15 248 VIII 27k Many vF stars 14..