DOCSLIB.ORG

Shape Comparison by Size Functions and Natural Size Distances

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Shape Comparison by Size Functions and Natural Size Distances RECENT ADVANCES IN MULTIDIMENSIONAL PERSISTENT TOPOLOGY Patrizio Frosini Vision Mathematics Group University of Bologna - Italy OUTLINE • Introduction and history • Multidimensional size functions • Reduction by the foliation method • Consequences: 1) STABILITY 2) LOCALIZATION OF DISCONTINUITIES • Conclusions Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 2/50 Let us start from three questions... Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 3/50 How similar are the colorings of these leaves? Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 4/50 How similar are the Riemannian structures of these manifolds? Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 5/50 How similar are the spatial positions of these wires? Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 6/50 All previous questions concern the comparison between pairs (M,ϕ), where M is a topological space and ϕ: M → IRk is a continuous function: ●LEAVES: ϕ(P)=color (r,g,b) at P ●3D MODELS: ϕ(P)=vector describing the first fundamental form at P •WIRES: ϕ(P)=(x(P),y(P),z(P)) Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 7/50 Multidimensional Persistent Topology studies the topological properties of the sublevel sets of continuous functions ϕ: M → IRk. It focuses on those properties that “persist” under change of the level. REMARK: the word multidimensional refers to the dimension of IRk, not the dimension of M! Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 8/50 From the beginning of the 90's, the study of Persistent Topology has originated different lines of research. Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 9/50 Persistence of connected components (size functions): P. Frosini, A distance for similarity classes of submanifolds of a Euclidean space, Bull. Austral. Math. Soc. 42, 3 (1990), 407-416. A. Verri, C. Uras, P. Frosini, M. Ferri, On the use of size functions for shape analysis, Biological Cybernetics, 70, (1993), 99-107. C. Uras, A. Verri, Computing Size Functions from Edge Maps, International Journal of Computer Vision, 23 (1997), n. 2, 169-183. F. Dibos, P. Frosini and D. Pasquignon, The use of Size Functions for Comparison of Shapes through Differential Invariants, Journal of Mathematical Imaging and Vision, 21, (2004), n. 2, 107-118. Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 10/50 Persistence in algebraic topological structures (size homotopy groups, size functor and persistent homology groups): P. Frosini, M. Mulazzani, Size homotopy groups for computation of natural size distances, Bull. Belg. Math. Soc., 6 (1999), 455-464. H. Edelsbrunner, D. Letscher and A. Zomorodian, Topological persistence and simplification, Discrete and Computational Geometry, 28 (2002), 511-533. F. Cagliari, M. Ferri and P. Pozzi, Size Functions from the categorical viewpoint, Acta Applicandae Mathematicae, 67 (2002), 225-235. G. Carlsson, A. Zomorodian, A. Collins and L. Guibas, Persistence barcodes for shapes, International Journal of Shape Modeling, 11(2) (2005), 149-187. D. Cohen-Steiner, H. Edelsbrunner, J. Harer, Stability of persistence diagrams, Discrete and Computational Geometry. 37(1) (2007), 103-120. Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 11/50 Natural pseudodistance (metric for persistence comparison) P. Donatini, P. Frosini, Natural pseudodistances between closed manifolds, Forum Mathematicum, 16 (2004), n. 5, 695-715. P. Donatini, P. Frosini, Natural pseudodistances between closed surfaces, Journal of the European Mathematical Society, 9 (2007), 331-353. P. Donatini, P. Frosini, Natural pseudodistances between closed curves, Forum Mathematicum (in press). Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 12/50 The natural pseudodistance Assume that M, N are topological spaces and ϕ : M→IRk, ψ : N→IRk are continuous functions. The natural pseudodistance between the pairs (M,ϕ), (N,ψ ) is defined to be where H(M,N) denotes the set of all homeomorphisms between M and N. Persistent topology can be also seen as a way to obtain lower bounds for the natural pseudodistance. Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 13/50 JUST TWO EXAMPLES... Size functions: Theorem. The matching distance between size functions is a lower bound for the natural pseudodistance. Size homotopy groups: Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 14/50 Multidimensional persistence P. Frosini, M. Mulazzani, Size homotopy groups for computation of natural size distances, Bull. Belg. Math. Soc. 6 (1999), 455-464). G. Carlsson, A. Zomorodian, The theory of multidimensional persistence homology, Proc. 2004 Eurographics/ACM SIGGRAPH Symposium on Geometry Processing. ACM Press, New York, NY, 184-193. S. Biasotti, A. Cerri, P. Frosini, D. Giorgi, C. Landi, Multidimensional size functions for shape comparison, Journal of Mathematical Imaging and Vision, 32 (2008), 161-179. Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 15/50 Surveys and general papers R. Ghrist, Barcodes: the persistent topology of data, Bull. Amer. Math. Soc., 45(1) (2008), 61-75. S. Biasotti, L. De Floriani, B. Falcidieno, P. Frosini, D. Giorgi, C. Landi, L. Papaleo, M. Spagnuolo, Describing shapes by geometrical-topological properties of real functions, ACM Computing Surveys, 40 (2008), n. 4, 12:1-12:87. H. Edelsbrunner, J.Harer, Persistent homology – a survey, Contemporary Mathematics, 453 (2008), 257-282. Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 16/50 Let us go back to size functions Size functions describe the shape of a topological k space M with respect to a function ϕ : Μ → IR . Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 17/50 NOTE: in the following of this talk we ≤ shall write x=(x1,…, xk ) y=(y1,…, yk ) to ≤ mean xi yi for every index i. Analogously, (x1,…, xk ) < (y1,…, yk ) will mean that xi < yi for every index i. Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 18/50 Definition of size function Let M be a topological space and assume that a continuous function ϕ : M →IRk is given. For each y ∈ IRk we denote by M 〈ϕ ≤ y〉 the set of all points of M at which the measuring function ϕ takes a value not greater than y. For each real vector y we say that two points P,Q are 〈ϕ ≤ y〉-connected if and only if they 〈ϕ ≤ 〉 belong to the same component in M y . Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 19/50 We call size function (of the pair (M,ϕ)) the ∆+ { ∈ 2k } → function ℓ (M,ϕ ): = (x,y) IR : x < y IN that takes each point (x,y) to the number of equivalence classes of M 〈ϕ ≤ x〉 with respect to 〈ϕ ≤ y〉-connectedness. EQUIVALENT DEFINITION ℓ(M,ϕ )(x,y) is the number of connected components of M〈ϕ ≤ y〉 that contain at least one point of M〈ϕ ≤ x〉. Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 20/50 Let us make the definition of size function clear by some example in the case k=1. Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 21/50 This is the size function ℓ(M,ϕ ). Example: M is the displayed curve, ϕ is the distance from C. Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 22/50 More details about our example Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 23/50 More details about our example Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 24/50 More details about our example Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 25/50 More details about our example Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 26/50 When we move to the multidimensional case (i.e. to the case of measuring functions taking values in IRk instead of IR) the domain of every size function is a subset of IR2k and many new problems arise. Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 27/50 ➔How can we represent size functions and persistent homology groups? Which distances can we use to compare size functions (or persistent homology groups)? ➔Are size functions and persistent homology groups stable with respect to small changes of the data? ➔Where are the discontinuities located, in the multidimensional case? Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 28/50 SOME NEW THEORETICAL RESULTS Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 29/50 REPRESENTATION BY FOLIATIONS Introduced in S. Biasotti, A. Cerri, P. Frosini, D. Giorgi, C. Landi, Multidimensional size functions for shape comparison, Journal of Mathematical Imaging and Vision, 32 (2008), 161-179. Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 30/50 The theory of k-dimensional size functions can be reduced to the theory of 1-dimensional size functions. Indeed, a parameterized family of half- planes in IRk x IRk exists such that the restriction of ℓ(M,ϕ ) to each of these half- planes can be seen as a particular 1- dimensional size function. Patrizio Frosini (U. Bologna) - MULTIDIMENSIONAL PERSISTENT TOPOLOGY 31/50 k For every unit vector u=(u1,…, uk ) of IR such that ui>0 for i=1,…,k and for every k Σ vector b=(b1,…, bk ) of IR such that i bi=0, we shall say that the pair (u,b) is admissible. Given an admissible pair (u,b), π k k we define the half-plane (u,b) of IR x IR by the following parametric equations: x=su+b s<t {y=tu+b Patrizio Frosini (U.
Load more

Recommended publications
  • Homology Inference from Point Cloud Data
    Homology Inference from Point Cloud Data Yusu Wang Abstract. In this paper, we survey a common framework of estimating topo- logical information from point cloud data (PCD) that has been developed in the field of computational topology in the past twenty years. Specifically, we focus on the inference of homological information. We briefly explain the main ingredients involved, and present some basic results. This chapter is part of the AMS short course on Geometry and Topology in Statistical Inference. It aims to introduce the general mathematical audience to the problem of topol- ogy inference, but is not meant to be a comprehensive review of the field in general. 1. Introduction The past two decades have witnessed tremendous development in the field of computational and applied topology. Much progress has been made not only in the theoretical and computational fronts, but also in the application of topological methods / ideas for data analysis. For example, on the theoretical front, there has been elegant work on the so-called persistent homology, originally proposed in [52] 1, and further developed in [15, 16, 19, 22, 33, 94] etc. On the application front, topological methods have been successfully used in fields such as computer graphics e.g, [67, 82, 42], visualization e.g, [10, 77, 76], geometric reconstruction and meshing e.g, [2, 41, 90], sensor network e.g, [38, 39, 61, 88, 91], high dimensional data analysis e.g, [59, 60, 84, 89] and so on. Indeed, topological data analysis (TDA) has become a vibrant field attracting researchers from mathematics, computer science and statistics.
    [Show full text]
  • Evolutionary Homology on Coupled Dynamical Systems
    Evolutionary homology on coupled dynamical systems Zixuan Cang1, Elizabeth Munch1;2 and Guo-Wei Wei1;3;4 ∗ 1 Department of Mathematics 2Department of Computational Mathematics, Science and Engineering 3 Department of Biochemistry and Molecular Biology 4 Department of Electrical and Computer Engineering Michigan State University, MI 48824, USA February 14, 2018 Abstract Time dependence is a universal phenomenon in nature, and a variety of mathematical models in terms of dynamical systems have been developed to understand the time-dependent behavior of real-world problems. Originally constructed to analyze the topological persistence over spatial scales, persistent homology has rarely been devised for time evolution. We propose the use of a new filtration function for persistent homology which takes as input the adjacent oscillator trajecto- ries of coupled dynamical systems. We also regulate the dynamical system by a weighted graph Laplacian matrix derived from the network of interest, which embeds the topological connectivity of the network into the dynamical system. The resulting topological signatures, which we call evolution- ary homology (EH) barcodes, reveal the topology-function relationship of the network and thus give rise to the quantitative analysis of nodal properties. The proposed EH is applied to protein residue networks for protein thermal fluctuation analysis, rendering the most accurate B-factor prediction of a set of 364 proteins. This work extends the utility of dynamical systems to the quantitative modeling and analysis of realistic physical systems. Contents 1 Introduction 2 2 Methods 4 2.1 Coupled dynamical systems . .4 arXiv:1802.04677v1 [math.AT] 13 Feb 2018 2.1.1 Systems configuration .
    [Show full text]
  • Computational Topology in Image Context Massimo Ferri, Patrizio Frosini, Claudia Landi and Barbara Di Fabio
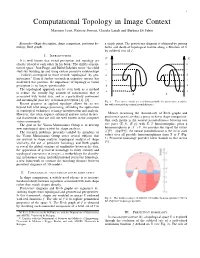
    1 Computational Topology in Image Context Massimo Ferri, Patrizio Frosini, Claudia Landi and Barbara Di Fabio Keywords—Shape description, shape comparison, persistent ho- a single point. The persistence diagram is obtained by pairing mology, Reeb graphs births and death of topological feature along a filtration of X by sublevel sets of f . I. INTRODUCTION f1 f2 It is well known that visual perception and topology are closely related to each other. In his book “The child’s concep- m m tion of space” Jean Piaget and Barbel¨ Inhelder wrote “the child e e starts by building up and using certain primitive relationships ... [which] correspond to those termed ‘topological’ by geo- d d metricians.” Even if further research in cognitive science has c c moderated this position, the importance of topology in visual perception is no longer questionable. b b The topological approach can be seen both as a method a a to reduce the usually big amount of information that is X Y associated with visual data, and as a particularly convenient and meaningful pass key to human perception [1], [2]. Fig. 1. Two curves which are not distinguishable by persistence modules, Recent progress in applied topology allows for its use but with nonvanishing natural pseudodistance. beyond low level image processing, extending the application of topological techniques to image interpretation and analysis. However, this often requires advanced and not trivial theoret- Metrics measuring the dissimilarity of Reeb graphs and ical frameworks that are still not well known in the computer persistence spaces are thus a proxy to direct shape comparison.
    [Show full text]
  • The Topology of Data
    techniques. In the approximation that the vacuum density is just the volume form on moduli space, the surface area of the boundary will just be thesurfaceareaoftheboundary in moduli space. Taking the region R to be a sphere in moduli space of radius r,wefind A(S1) √K Developing Topological Observables V (S1) ∼ r so the condition Eq. (5.2) becomes K L> . (5.3) in Cosmology r2 Thus, if we consider a large enough region, or the entire moduli space in order to find the total number of vacua, the condition for the asymptotic vacuum counting formulas we have discussed in this work to hold is L>cKwith some order one coe∼cient. But if we Alex Cole subdivide the region into subregions which do not satisfy Eq.(5.3),wewillfindthatthe number of vacua in each subregion will show oscillations around this centralThe scaling. In Topology of Data:PhD Thesis Defense fact, most regions will contain a smaller number of vacua (like S above), while a few should ∼ August 12, 2020 have anomalously large numbers (like S above), averaging out toFrom Eq. (5.1). String Theory to Cosmology to Phases of Matter 5.1 Flux vacua on rigid Calabi-Yau As an illustration of this, consider the following toy problem with K =4,studiedin[1].Theconfiguration space is simply the fundamental region of the upper 3 half plane, parameterized by ∼.Thefluxsuperpoten- tials are taken to be W = A∼ + B with A = a1 + ia2 and B = b1 + ib2 each taking values 2 in Z+iZ.Thiswouldbeobtainedifweconsideredflux vacua on a rigid Calabi-Yau, with no complex structure moduli, b3 =2,andtheperiods√1 =1and√2 = i.
    [Show full text]
  • Arxiv:0811.1868V2 [Cs.CG]
    NECESSARY CONDITIONS FOR DISCONTINUITIES OF MULTIDIMENSIONAL SIZE FUNCTIONS A. CERRI AND P. FROSINI Abstract. Some new results about multidimensional Topological Persistence are presented, proving that the discontinuity points of a k-dimensional size function are necessarily related to the pseudocritical or special values of the associated measuring function. Introduction Topological Persistence is devoted to the study of stable properties of sublevel sets of topological spaces and, in the course of its development, has revealed itself to be a suitable framework when dealing with applications in the field of Shape Analysis and Comparison. Since the beginning of the 1990s research on this sub- ject has been carried out under the name of Size Theory, studying the concept of size function, a mathematical tool able to describe the qualitative properties of a shape in a quantitative way. More precisely, the main idea is to model a shape by a topological space endowed with a continuous function ϕ, called measuring function. Such a functionM is chosen according to applications and can be seen as a descriptor of the features considered relevant for shape characterization. Under these assumptions, the size function ℓ( ,ϕ) associated with the pair ( , ϕ) is a de- scriptor of the topological attributes thatM persist in the sublevel setsM of induced by the variation of ϕ. According to this approach, the problem of comparingM two shapes can be reduced to the simpler comparison of the related size functions. Since their introduction, these shape descriptors have been widely studied and applied in quite a lot of concrete applications concerning Shape Comparison and Pattern Recognition (cf., e.g., [4, 8, 15, 34, 35, 36]).
    [Show full text]
  • Size Functions for Shape Recognition in the Presence of Occlusions
    Size functions for shape recognition in the presence of occlusions Barbara Di Fabio1 Claudia Landi2∗ 1Dipartimento di Matematica, Universita` di Bologna, Italia 2Dipartimento di Scienze e Metodi dell'Ingegneria, Universita` di Modena e Reggio Emilia, Italia September 2, 2009 Abstract In Computer Vision the ability to recognize objects in the presence of occlusions is a necessary requirement for any shape representation method. In this paper we investigate how the size function of an object shape changes when a portion of the object is occluded by another object. More precisely, considering a set X = A [ B and a measuring function ϕ on X, we establish a condition so that `(X;j) = `(A;jjA) + `(B;jjB) − `(A\B;jjA\B). The main tool we use is the Mayer-Vietoris sequence of Cechˇ homology groups. This result allows us to prove that size functions are able to detect partial matching between shapes by showing a common subset of cornerpoints. Keywords: Cechˇ homology, Mayer-Vietoris sequence, persistent homology, shape occlusion MSC (2000): 55N05, 68U05 1 Introduction Shape matching and retrieval are key aspects in the design of search engines based on visual, rather than keyword, information. Generally speaking, shape matching methods rely on the computation of a shape description, also called a signature, that effectively captures some essential features of the object. The ability to perform not only global matching, but also partial matching, is regarded as one of the most meaningful properties in order to evaluate the performance of a shape matching method (cf., e.g., [36]). Basically, the interest in robustness against partial occlusions is motivated by the problem of recognizing an object partially hidden by some other foreground object in the same image.
    [Show full text]
  • Algebraic Topological Methods in Computer Science (Atmcs) Iii
    ALGEBRAIC TOPOLOGICAL METHODS IN COMPUTER SCIENCE (ATMCS) III Paris, France July 7-11, 2008 1 2 ALGEBRAIC TOPOLOGICAL METHODS IN COMPUTER SCIENCE (ATMCS) III July 7 8:00 8:50 refreshments and orientation 8:50 9:00 opening remarks 9:00 10:00 invited talk Trace spaces: Organization, calculations, applications (Martin Raussen) 10:00 10:15 break 10:15 11:15 invited talk (Timothy Porter) 11:15 11:30 break 11:30 12:00 Geometric databases (David Spivak) 12:00 12:30 Simulation hemi-metrics for timed Systems, with relations to ditopology (Uli Fahren- berg) 12:30 14:30 lunch 14:30 15:30 invited talk Computation and the periodic table (John Baez) 15:30 15:45 break 15:45 16:45 invited talk Structure discovery, routing and information brokerage in sensor net- works (Leonidas Guibas) 16:45 17:00 break 17:00 17:30 Topological methods for predicting the character of response surface z = f(x; y) while elastomer systems studying (Ilya Gorelkin) 17:30 18:00 Extremal models of concurrent systems, the fundamental bipartite graph, and di- rected van Kampen theorems (Peter Bubenik) The end of the booklet contains all available abstracts, in alphabetical order of presenter. ALGEBRAIC TOPOLOGICAL METHODS IN COMPUTER SCIENCE (ATMCS) III 3 July 8 8:30 9:00 refreshments 9:00 10:00 invited talk (speaker Dmitry Kozlov) 10:00 10:15 break 10:15 11:15 invited talk Locally ordered spaces as sheaves (Krzysztof Worytkiewicz) 11:15 11:30 break 11:30 12:30 A survey on homological perturbation theory (Johannes Huebschmann) 12:30 14:30 lunch 14:30 15:30 invited talk Path categories
    [Show full text]
  • Proceedings in a Single
    Schedule of Talks 27th Annual Fall Workshop on Computational Geometry November 3–4, 2017 Stony Brook University Stony Brook, NY Sponsored by the National Science Foundation and the Department of Applied Mathematics and Statistics and the Department of Computer Science, College of Engineering and Applied Sciences, Stony Brook University Program Committee: GregAloupis(Tufts) PeterBrass(CCNY) WilliamRandolphFranklin(RPI) JieGao(co-chair,StonyBrook) MayankGoswami(QueensCollege) MatthewP.Johnson(Lehman College) Joseph S. B. Mitchell (co-chair, Stony Brook) Don Sheehy (University of Connecticut) Jinhui Xu (University at Buffalo) Friday, November 3, 2017: Computer Science (NCS), Room 120 9:20 Opening remarks Contributed Session 1 Chair: Joe Mitchell 9:30–9:45 “Sampling Conditions for Clipping-free Voronoi Meshing by the VoroCrust Algorithm”, Scott Mitchell, Ahmed Abdelkader, Ahmad Rushdi, Mohamed Ebeida, Ahmed Mahmoud, John Owens and Chandrajit Bajaj 9:45–10:00 “Quasi-centroidal Simplicial Meshes for Optimal Variational Methods”, Xiangmin Jiao 10:00–10:15 “A Parallel Approach for Computing Discrete Gradients on Mulfiltrations”, Federico Iuricich, Sara Scaramuccia, Claudia Landi and Leila De Floriani 10:15–10:30 “Parallel Intersection Detection in Massive Sets of Cubes”, W. Randolph Franklin and Salles V.G. Magalh˜aes 10:30–11:00 Break. Contributed Session 2 Chair: Jie Gao 11:00–11:15 “Dynamic Orthogonal Range Searching on the RAM, Revisited”, Timothy M. Chan and Konstantinos Tsakalidis 11:15–11:30 “Faster Algorithm for Truth Discovery via Range
    [Show full text]
  • Dipartimento Di Informatica, Bioingegneria, Robotica Ed Ingegneria Dei Sistemi
    Dipartimento di Informatica, Bioingegneria, Robotica ed Ingegneria dei Sistemi Computational and Theoretical Issues of Multiparameter Persistent Homology for Data Analysis by Sara Scaramuccia Theses Series DIBRIS-TH-2018-16 DIBRIS, Università di Genova Via Opera Pia, 13 16145 Genova, Italy http://www.dibris.unige.it/ Università degli Studi di Genova Dipartimento di Informatica, Bioingegneria, Robotica ed Ingegneria dei Sistemi Ph.D. Thesis in Computer Science and Systems Engineering Computer Science Curriculum Computational and Theoretical Issues of Multiparameter Persistent Homology for Data Analysis by Sara Scaramuccia May, 2018 Dottorato di Ricerca in Informatica ed Ingegneria dei Sistemi Indirizzo Informatica Dipartimento di Informatica, Bioingegneria, Robotica ed Ingegneria dei Sistemi Università degli Studi di Genova DIBRIS, Univ. di Genova Via Opera Pia, 13 I-16145 Genova, Italy http://www.dibris.unige.it/ Ph.D. Thesis in Computer Science and Systems Engineering Computer Science Curriculum (S.S.D. INF/01) Submitted by Sara Scaramuccia DIBRIS, Univ. di Genova [email protected] Date of submission: January 2018 Title: Computational and Theoretical Issues of Multiparameter Persistent Homology for Data Analysis Advisors: Leila De Floriani Dipartimento di Informatica, Bioingegneria, Robotica ed Ingegneria dei Sistemi Università di Genova, Italy leila.defl[email protected] Claudia Landi Dipartimento di Scienze e Metodi dell’Ingegneria Università di Modena e Reggio Emilia, Italy [email protected] Ext. Reviewers: *Silvia Biasotti, `Heike Leitte *Istituto di Matematica Applicata e Tecnologie Informatiche "Enrico Magenes" Consiglio Nazionale delle Ricerche: Genova, Italy [email protected] ` Fachbereich Informatik Technische Universität Kaiserslautern, Germany [email protected] 4 Abstract The basic goal of topological data analysis is to apply topology-based descriptors to understand and describe the shape of data.
    [Show full text]
  • Persistence, Metric Invariants, and Simplification
    Persistence, Metric Invariants, and Simplification Dissertation Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Osman Berat Okutan, M.S. Graduate Program in Mathematics The Ohio State University 2019 Dissertation Committee: Facundo M´emoli,Advisor Matthew Kahle Jean-Franc¸oisLafont c Copyright by Osman Berat Okutan 2019 Abstract Given a metric space, a natural question to ask is how to obtain a simpler and faithful approximation of it. In such a situation two main concerns arise: How to construct the approximating space and how to measure and control the faithfulness of the approximation. In this dissertation, we consider the following simplification problems: Finite approx- imations of compact metric spaces, lower cardinality approximations of filtered simplicial complexes, tree metric approximations of metric spaces and finite metric graph approxima- tions of compact geodesic spaces. In each case, we give a simplification construction, and measure the faithfulness of the process by using the metric invariants of the original space, including the Vietoris-Rips persistence barcodes. ii For Esra and Elif Beste iii Acknowledgments First and foremost I'd like to thank my advisor, Facundo M´emoli,for our discussions and for his continual support, care and understanding since I started working with him. I'd like to thank Mike Davis for his support especially on Summer 2016. I'd like to thank Dan Burghelea for all the courses and feedback I took from him. Finally, I would like to thank my wife Esra and my daughter Elif Beste for their patience and support.
    [Show full text]
  • Multidimensional Size Functions for Shape Comparison
    J Math Imaging Vis DOI 10.1007/s10851-008-0096-z Multidimensional Size Functions for Shape Comparison S. Biasotti · A. Cerri · P. Frosini · D. Giorgi · C. Landi © Springer Science+Business Media, LLC 2008 Abstract Size Theory has proven to be a useful framework proof of their stability with respect to that distance. Experi- for shape analysis in the context of pattern recognition. Its ments are carried out to show the feasibility of the method. main tool is a shape descriptor called size function. Size Theory has been mostly developed in the 1-dimensional set- Keywords Multidimensional size function · ting, meaning that shapes are studied with respect to func- Multidimensional measuring function · Natural tions, defined on the studied objects, with values in R.The pseudo-distance potentialities of the k-dimensional setting, that is using func- tions with values in Rk, were not explored until now for lack of an efficient computational approach. In this paper we pro- 1 Introduction vide the theoretical results leading to a concise and complete shape descriptor also in the multidimensional case. This is In the shape analysis literature many methods have been de- possible because we prove that in Size Theory the compar- veloped, which describe shapes making use of properties ison of multidimensional size functions can be reduced to of real-valued functions defined on the studied object. Usu- the 1-dimensional case by a suitable change of variables. In- ally, the role of these functions is to quantitatively measure deed, a foliation in half-planes can be given, such that the re- the geometric properties of the shape while taking into ac- striction of a multidimensional size function to each of these count its topology.
    [Show full text]
  • Size Theory and Shape Matching: a Survey
    Size Theory and Shape Matching: A Survey Yi Ding December 11, 2008 Abstract This paper investigates current research on size theory. The re- search reviewed in this paper includes studies on 1-D size theory, multi- dimensional size theory and their applications to shape matching. This survey will also address the connections between the size theoretical approach and other approaches to shape matching. 1 Introduction Originally proposed as a method for comparison between manifolds, size theory(cf. [1] [5] [6] [7] [8] [9] [10] [11]) is a new approach towards geomet- rical/topological shape matching. In a size theoretical framework a shape is described by a size pair ( , φ), where φ : Rk is a k-dimensional M M → measuring function. Natural pseudo-distance and matching distances are two important and related dissimilarity measures between size pairs. The natural pseudo-distance between size pairs ( , φ) and ( , ψ) is M N defined as inff Hom( , ) maxP φ(P ) ψ(f(P )) . Despite its beautiful ∈ M N ∈M | − | geometric formulation, the natural pseudo-distance is very difficult to com- pute since the infimum is taken over all the homeomorphisms between M and . The matching distance dmatch between reduced size functions, be- N ing an easily computable lower bound, is proposed in [6] as an alternative matching function. The 1-D size function does not generalize readily to the multidimensional case, some care must be taken in choosing a suitable foliation. The reduced size function basically studies the connectedness of sub-level sets. Other 1 types of lower bounds also exists, for example, Frosini et.al [11] proposed a lower bound based on size homotopy groups.
    [Show full text]