DOCSLIB.ORG

Dipartimento Di Informatica, Bioingegneria, Robotica Ed Ingegneria Dei Sistemi

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Dipartimento Di Informatica, Bioingegneria, Robotica Ed Ingegneria Dei Sistemi Dipartimento di Informatica, Bioingegneria, Robotica ed Ingegneria dei Sistemi Computational and Theoretical Issues of Multiparameter Persistent Homology for Data Analysis by Sara Scaramuccia Theses Series DIBRIS-TH-2018-16 DIBRIS, Università di Genova Via Opera Pia, 13 16145 Genova, Italy http://www.dibris.unige.it/ Università degli Studi di Genova Dipartimento di Informatica, Bioingegneria, Robotica ed Ingegneria dei Sistemi Ph.D. Thesis in Computer Science and Systems Engineering Computer Science Curriculum Computational and Theoretical Issues of Multiparameter Persistent Homology for Data Analysis by Sara Scaramuccia May, 2018 Dottorato di Ricerca in Informatica ed Ingegneria dei Sistemi Indirizzo Informatica Dipartimento di Informatica, Bioingegneria, Robotica ed Ingegneria dei Sistemi Università degli Studi di Genova DIBRIS, Univ. di Genova Via Opera Pia, 13 I-16145 Genova, Italy http://www.dibris.unige.it/ Ph.D. Thesis in Computer Science and Systems Engineering Computer Science Curriculum (S.S.D. INF/01) Submitted by Sara Scaramuccia DIBRIS, Univ. di Genova [email protected] Date of submission: January 2018 Title: Computational and Theoretical Issues of Multiparameter Persistent Homology for Data Analysis Advisors: Leila De Floriani Dipartimento di Informatica, Bioingegneria, Robotica ed Ingegneria dei Sistemi Università di Genova, Italy leila.defl[email protected] Claudia Landi Dipartimento di Scienze e Metodi dell’Ingegneria Università di Modena e Reggio Emilia, Italy [email protected] Ext. Reviewers: *Silvia Biasotti, `Heike Leitte *Istituto di Matematica Applicata e Tecnologie Informatiche "Enrico Magenes" Consiglio Nazionale delle Ricerche: Genova, Italy [email protected] ` Fachbereich Informatik Technische Universität Kaiserslautern, Germany [email protected] 4 Abstract The basic goal of topological data analysis is to apply topology-based descriptors to understand and describe the shape of data. In this context, homology is one of the most relevant topological descriptors, well-appreciated for its discrete nature, computability and dimension independence. A further development is provided by persistent homology, which allows to track homological features along a one- parameter increasing sequence of spaces. Multiparameter persistent homology, also called multipersistent homology, is an extension of the theory of persistent homology motivated by the need of analyzing data naturally described by several parameters, such as vector-valued functions. Multipersistent homology presents several issues in terms of feasibility of computations over real-sized data and theoretical challenges in the evaluation of possible descriptors. The focus of this thesis is in the interplay between persistent homology theory and discrete Morse Theory. Discrete Morse theory provides methods for reducing the computational cost of homology and persis- tent homology by considering the discrete Morse complex generated by the discrete Morse gradient in place of the original complex. The work of this thesis addresses the problem of computing multipersistent homology, to make such tool usable in real application domains. This requires both computational optimizations towards the applications to real-world data, and theoretical insights for finding and interpreting suitable descriptors. Our computational contribution consists in proposing a new Morse-inspired and fully discrete preprocessing algorithm. We show the feasibility of our preprocessing over real datasets, and evaluate the impact of the proposed algorithm as a preprocessing for computing multipersistent homology. A theoretical contribution of this thesis consists in proposing a new notion of optimality for such a preprocessing in the multiparameter context. We show that the proposed notion generalizes an already known optimality notion from the one-parameter case. Under this definition, we show that the algorithm we propose as a preprocessing is optimal in low dimensional domains. In the last part of the thesis, we consider preliminary applications of the proposed algorithm in the context of topology-based multivariate visualization by tracking critical features generated by a discrete gradient field com- patible with the multiple scalar fields under study. We discuss (dis)similarities of such critical features with the state-of-the-art techniques in topology-based multivariate data visualization. i Contents List of Figures ix List of Tables xiii Introduction xv 1 Background notions1 1.1 Cell complexes...................................1 1.1.1 Simplicial complexes............................2 1.1.2 Cubical and cell complexes.........................4 1.2 Homology......................................7 1.2.1 Simplicial chain complexes........................8 1.3 Lefschetz complexes................................ 10 1.3.1 Relative homology and Mayer-Vietoris pairs............... 12 1.4 Discrete Morse Theory............................... 14 1.4.1 Basic notions in discrete Morse Theory.................. 14 1.4.2 Discrete Morse complex.......................... 16 1.5 One-parameter persistent homology........................ 17 1.5.1 One-parameter filtrations.......................... 18 1.5.2 One-parameter persistence module..................... 19 1.6 Multiparameter persistent homology........................ 21 1.6.1 Multiparameter filtrations......................... 21 1.6.2 Multiparameter persistence module.................... 23 1.7 Invariants in persistent homology.......................... 24 iii 1.7.1 Invariants in one-persistent homology................... 25 1.7.2 Invariants in multipersistent homology................... 27 1.7.3 Algebraic invariants in persistent homology................ 30 2 State of the art 35 2.1 Data structures representing simplicial and cell complexes............ 35 2.2 Filtrations...................................... 36 2.3 Computing one-persistent homology........................ 37 2.3.1 Integrated one-parameter techniques.................... 39 2.3.2 Preprocessing in one-persistent homology................. 40 2.3.3 Tools for one-persistent homology..................... 41 2.3.4 Discussion................................. 42 2.4 Computing multipersistent homology....................... 43 2.4.1 Invariants in multipersistent homology................... 44 2.4.2 Computing multipersistent descriptors................... 47 2.4.3 Preprocessing in multipersistent homology................ 50 2.4.4 Discussion................................. 51 2.5 Interpreting invariants in persistent homology................... 51 2.5.1 Distances between invariants........................ 52 2.5.2 Stability................................... 53 2.5.3 Towards Statistics.............................. 54 2.6 Discussion...................................... 54 3 Preliminaries on Morse-based preprocessings for persistence 55 3.1 Finding a discrete gradient over a single lower star: HomotopyExpansion ................................ 56 3.1.1 Input and output formalization....................... 56 3.1.2 Description................................. 58 3.1.3 Complexity remarks............................ 62 iv 3.2 A local preprocessing algorithm for one-persistent homology: ProcessLowerStars ................................. 63 3.2.1 Input and output formalization....................... 63 3.2.2 Description................................. 66 3.2.3 Complexity remarks............................ 67 3.3 A global preprocessing algorithm for multipersistent homology: Matching ...................................... 68 3.3.1 Input and output formalization....................... 69 3.3.2 Description................................. 71 3.3.3 Complexity remarks............................ 73 4 A local Morse-based preprocessing algorithm for multipersistent homology: ComputeDiscreteGradient 77 4.1 Input and output formalization........................... 77 4.2 Well-extensible indexing.............................. 78 4.3 Algorithm description................................ 80 4.3.1 Auxiliary functions............................. 82 4.4 Complexity..................................... 84 4.4.1 Analysis.................................. 84 4.4.2 Discussion................................. 87 4.5 Correctness..................................... 89 4.5.1 Corresponding partitions.......................... 90 4.5.2 ComputeDiscreteGradient and Matching are equivalent......... 91 4.6 From a discrete gradient to the Morse complex: BoundaryMaps ................................... 93 4.6.1 Input and output formalization....................... 93 4.6.2 Description in the simplicial case..................... 94 4.6.3 Description in the cubical case....................... 96 5 Optimality by relative homology 99 v 5.1 One-parameter optimality in terms of relative homology............. 99 5.2 Multiparameter optimality............................. 104 5.3 Filtered Morse complexes preserve relative homology............... 106 5.4 Algorithm ComputeDiscreteGradient is optimal................. 108 5.4.1 Optimality for 3D regular grids...................... 108 5.4.2 Optimality for abstract simplicial 2-complexes.............. 108 6 Experimental analysis and evaluation 113 6.1 Comparison to the Matching Algorithm...................... 113 6.1.1 Method................................... 113 6.1.2 Implementation............................... 114 6.1.3 Results................................... 115 6.1.4 Discussion................................. 116 6.2 Impact on the computation
Load more

Recommended publications
  • Topology and Data
    BULLETIN (New Series) OF THE AMERICAN MATHEMATICAL SOCIETY Volume 46, Number 2, April 2009, Pages 255–308 S 0273-0979(09)01249-X Article electronically published on January 29, 2009 TOPOLOGY AND DATA GUNNAR CARLSSON 1. Introduction An important feature of modern science and engineering is that data of various kinds is being produced at an unprecedented rate. This is so in part because of new experimental methods, and in part because of the increase in the availability of high powered computing technology. It is also clear that the nature of the data we are obtaining is significantly different. For example, it is now often the case that we are given data in the form of very long vectors, where all but a few of the coordinates turn out to be irrelevant to the questions of interest, and further that we don’t necessarily know which coordinates are the interesting ones. A related fact is that the data is often very high-dimensional, which severely restricts our ability to visualize it. The data obtained is also often much noisier than in the past and has more missing information (missing data). This is particularly so in the case of biological data, particularly high throughput data from microarray or other sources. Our ability to analyze this data, both in terms of quantity and the nature of the data, is clearly not keeping pace with the data being produced. In this paper, we will discuss how geometry and topology can be applied to make useful contributions to the analysis of various kinds of data.
    [Show full text]
  • Algebraic Topology
    Algebraic Topology Vanessa Robins Department of Applied Mathematics Research School of Physics and Engineering The Australian National University Canberra ACT 0200, Australia. email: [email protected] September 11, 2013 Abstract This manuscript will be published as Chapter 5 in Wiley's textbook Mathe- matical Tools for Physicists, 2nd edition, edited by Michael Grinfeld from the University of Strathclyde. The chapter provides an introduction to the basic concepts of Algebraic Topology with an emphasis on motivation from applications in the physical sciences. It finishes with a brief review of computational work in algebraic topology, including persistent homology. arXiv:1304.7846v2 [math-ph] 10 Sep 2013 1 Contents 1 Introduction 3 2 Homotopy Theory 4 2.1 Homotopy of paths . 4 2.2 The fundamental group . 5 2.3 Homotopy of spaces . 7 2.4 Examples . 7 2.5 Covering spaces . 9 2.6 Extensions and applications . 9 3 Homology 11 3.1 Simplicial complexes . 12 3.2 Simplicial homology groups . 12 3.3 Basic properties of homology groups . 14 3.4 Homological algebra . 16 3.5 Other homology theories . 18 4 Cohomology 18 4.1 De Rham cohomology . 20 5 Morse theory 21 5.1 Basic results . 21 5.2 Extensions and applications . 23 5.3 Forman's discrete Morse theory . 24 6 Computational topology 25 6.1 The fundamental group of a simplicial complex . 26 6.2 Smith normal form for homology . 27 6.3 Persistent homology . 28 6.4 Cell complexes from data . 29 2 1 Introduction Topology is the study of those aspects of shape and structure that do not de- pend on precise knowledge of an object's geometry.
    [Show full text]
  • Homology Inference from Point Cloud Data
    Homology Inference from Point Cloud Data Yusu Wang Abstract. In this paper, we survey a common framework of estimating topo- logical information from point cloud data (PCD) that has been developed in the field of computational topology in the past twenty years. Specifically, we focus on the inference of homological information. We briefly explain the main ingredients involved, and present some basic results. This chapter is part of the AMS short course on Geometry and Topology in Statistical Inference. It aims to introduce the general mathematical audience to the problem of topol- ogy inference, but is not meant to be a comprehensive review of the field in general. 1. Introduction The past two decades have witnessed tremendous development in the field of computational and applied topology. Much progress has been made not only in the theoretical and computational fronts, but also in the application of topological methods / ideas for data analysis. For example, on the theoretical front, there has been elegant work on the so-called persistent homology, originally proposed in [52] 1, and further developed in [15, 16, 19, 22, 33, 94] etc. On the application front, topological methods have been successfully used in fields such as computer graphics e.g, [67, 82, 42], visualization e.g, [10, 77, 76], geometric reconstruction and meshing e.g, [2, 41, 90], sensor network e.g, [38, 39, 61, 88, 91], high dimensional data analysis e.g, [59, 60, 84, 89] and so on. Indeed, topological data analysis (TDA) has become a vibrant field attracting researchers from mathematics, computer science and statistics.
    [Show full text]
  • NECESSARY CONDITIONS for DISCONTINUITIES of MULTIDIMENSIONAL SIZE FUNCTIONS Introduction Topological Persistence Is Devoted to T
    NECESSARY CONDITIONS FOR DISCONTINUITIES OF MULTIDIMENSIONAL SIZE FUNCTIONS A. CERRI AND P. FROSINI Abstract. Some new results about multidimensional Topological Persistence are presented, proving that the discontinuity points of a k-dimensional size function are necessarily related to the pseudocritical or special values of the associated measuring function. Introduction Topological Persistence is devoted to the study of stable properties of sublevel sets of topological spaces and, in the course of its development, has revealed itself to be a suitable framework when dealing with applications in the field of Shape Analysis and Comparison. Since the beginning of the 1990s research on this sub- ject has been carried out under the name of Size Theory, studying the concept of size function, a mathematical tool able to describe the qualitative properties of a shape in a quantitative way. More precisely, the main idea is to model a shape by a topological space endowed with a continuous function ϕ, called measuring function. Such a functionM is chosen according to applications and can be seen as a descriptor of the features considered relevant for shape characterization. Under these assumptions, the size function ℓ( ,ϕ) associated with the pair ( , ϕ) is a de- scriptor of the topological attributes thatM persist in the sublevel setsM of induced by the variation of ϕ. According to this approach, the problem of comparingM two shapes can be reduced to the simpler comparison of the related size functions. Since their introduction, these shape descriptors have been widely studied and applied in quite a lot of concrete applications concerning Shape Comparison and Pattern Recognition (cf., e.g., [4, 8, 15, 34, 35, 36]).
    [Show full text]
  • 25 HIGH-DIMENSIONAL TOPOLOGICAL DATA ANALYSIS Fr´Ed´Ericchazal
    25 HIGH-DIMENSIONAL TOPOLOGICAL DATA ANALYSIS Fr´ed´ericChazal INTRODUCTION Modern data often come as point clouds embedded in high-dimensional Euclidean spaces, or possibly more general metric spaces. They are usually not distributed uniformly, but lie around some highly nonlinear geometric structures with nontriv- ial topology. Topological data analysis (TDA) is an emerging field whose goal is to provide mathematical and algorithmic tools to understand the topological and geometric structure of data. This chapter provides a short introduction to this new field through a few selected topics. The focus is deliberately put on the mathe- matical foundations rather than specific applications, with a particular attention to stability results asserting the relevance of the topological information inferred from data. The chapter is organized in four sections. Section 25.1 is dedicated to distance- based approaches that establish the link between TDA and curve and surface re- construction in computational geometry. Section 25.2 considers homology inference problems and introduces the idea of interleaving of spaces and filtrations, a funda- mental notion in TDA. Section 25.3 is dedicated to the use of persistent homology and its stability properties to design robust topological estimators in TDA. Sec- tion 25.4 briefly presents a few other settings and applications of TDA, including dimensionality reduction, visualization and simplification of data. 25.1 GEOMETRIC INFERENCE AND RECONSTRUCTION Topologically correct reconstruction of geometric shapes from point clouds is a classical problem in computational geometry. The case of smooth curve and surface reconstruction in R3 has been widely studied over the last two decades and has given rise to a wide range of efficient tools and results that are specific to dimensions 2 and 3; see Chapter 35.
    [Show full text]
  • Multiset Metrics on Bounded Spaces
    Multiset metrics on bounded spaces∗ Stephen M. Turner Abstract We discuss five simple functions on finite multisets of metric spaces. The first four are all metrics iff the underlying space is bounded and are complete metrics iff it is also complete. Two of them, and the fifth func- tion, all generalise the usual Hausdorff metric on subsets. Some possible applications are also considered. 1 Introduction Metrics on subsets and multisets (subsets-with-repetition-allowed) of metric spaces have or could have numerous fields of application such as credit rating, pattern or image recognition and synthetic biology. We employ three related models (called E, F and G) for the space of multisets on the metric space (X, d). On each of E, F we define two closely-related functions. These four functions all turn out to be metrics precisely when d is bounded, and are complete iff d is also complete. Another function studied in model G has the same properties for (at least) uniformly discrete d. X is likely to be finite in many applications anyway. We show that there is an integer programming algorithm for those in model E. The three in models F and G generalise the Hausdorff metric. Beyond finiteness, no assumptions about multiset sizes are required. Various types of multiset metric on sets have been described[1.3], but the few that incorporate an underlying metric only refer to R or C. The simple and more general nature of those described here suggests that there may be other interesting possibilities. In this section, after setting out notation and required background, we men- tion briefly the existing work in this field.
    [Show full text]
  • Evolutionary Homology on Coupled Dynamical Systems
    Evolutionary homology on coupled dynamical systems Zixuan Cang1, Elizabeth Munch1;2 and Guo-Wei Wei1;3;4 ∗ 1 Department of Mathematics 2Department of Computational Mathematics, Science and Engineering 3 Department of Biochemistry and Molecular Biology 4 Department of Electrical and Computer Engineering Michigan State University, MI 48824, USA February 14, 2018 Abstract Time dependence is a universal phenomenon in nature, and a variety of mathematical models in terms of dynamical systems have been developed to understand the time-dependent behavior of real-world problems. Originally constructed to analyze the topological persistence over spatial scales, persistent homology has rarely been devised for time evolution. We propose the use of a new filtration function for persistent homology which takes as input the adjacent oscillator trajecto- ries of coupled dynamical systems. We also regulate the dynamical system by a weighted graph Laplacian matrix derived from the network of interest, which embeds the topological connectivity of the network into the dynamical system. The resulting topological signatures, which we call evolution- ary homology (EH) barcodes, reveal the topology-function relationship of the network and thus give rise to the quantitative analysis of nodal properties. The proposed EH is applied to protein residue networks for protein thermal fluctuation analysis, rendering the most accurate B-factor prediction of a set of 364 proteins. This work extends the utility of dynamical systems to the quantitative modeling and analysis of realistic physical systems. Contents 1 Introduction 2 2 Methods 4 2.1 Coupled dynamical systems . .4 arXiv:1802.04677v1 [math.AT] 13 Feb 2018 2.1.1 Systems configuration .
    [Show full text]
  • Topological Methods for 3D Point Cloud Processing
    Topological Methods for 3D Point Cloud Processing A DISSERTATION SUBMITTED TO THE FACULTY OF THE GRADUATE SCHOOL OF THE UNIVERSITY OF MINNESOTA BY William Joseph Beksi IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF Doctor of Philosophy Nikolaos Papanikolopoulos, Adviser August, 2018 c William Joseph Beksi 2018 ALL RIGHTS RESERVED Acknowledgements First and foremost, I thank my adviser Nikolaos Papanikolopoulos. Nikos was the first person in my career to see my potential and give me the freedom to pursue my own research interests. My success is a direct result of his advice, encouragement, and support over the years. I am beholden to my labmates at the Center for Distributed Robotics for their questions, comments, and healthy criticism of my work. I'm especially grateful to Duc Fehr for letting me get involved in his research as a new member of the lab. I also thank all of my committee members for their feedback through out this entire process. The inspiration for this research is due to the Institute for Mathematics and its Applications (IMA) located at the University of Minnesota. Each year the IMA explores a theme in applied mathematics through a series of tutorials, workshops, and seminars. It was during the Scientific and Engineering Applications of Algebraic Topology (2013- 2014) that I began to conceive of the ideas for this thesis. This work would not be possible without the computational, storage, and software resources provided by the Minnesota Supercomputing Institute (MSI) and its excellent staff. I especially thank Jeffrey McDonald for his friendship and support. I acknowledge and thank the National Science Foundation (NSF) for supporting this research and the University of Minnesota Informatics Institute (UMII) for funding my fellowship.
    [Show full text]
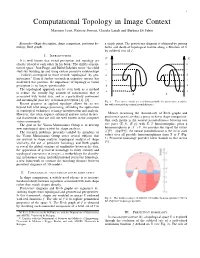
  • Computational Topology in Image Context Massimo Ferri, Patrizio Frosini, Claudia Landi and Barbara Di Fabio
    1 Computational Topology in Image Context Massimo Ferri, Patrizio Frosini, Claudia Landi and Barbara Di Fabio Keywords—Shape description, shape comparison, persistent ho- a single point. The persistence diagram is obtained by pairing mology, Reeb graphs births and death of topological feature along a filtration of X by sublevel sets of f . I. INTRODUCTION f1 f2 It is well known that visual perception and topology are closely related to each other. In his book “The child’s concep- m m tion of space” Jean Piaget and Barbel¨ Inhelder wrote “the child e e starts by building up and using certain primitive relationships ... [which] correspond to those termed ‘topological’ by geo- d d metricians.” Even if further research in cognitive science has c c moderated this position, the importance of topology in visual perception is no longer questionable. b b The topological approach can be seen both as a method a a to reduce the usually big amount of information that is X Y associated with visual data, and as a particularly convenient and meaningful pass key to human perception [1], [2]. Fig. 1. Two curves which are not distinguishable by persistence modules, Recent progress in applied topology allows for its use but with nonvanishing natural pseudodistance. beyond low level image processing, extending the application of topological techniques to image interpretation and analysis. However, this often requires advanced and not trivial theoret- Metrics measuring the dissimilarity of Reeb graphs and ical frameworks that are still not well known in the computer persistence spaces are thus a proxy to direct shape comparison.
    [Show full text]
  • Quantum Algorithms for Topological and Geometric Analysis of Data
    Quantum algorithms for topological and geometric analysis of data The MIT Faculty has made this article openly available. Please share how this access benefits you. Your story matters. Citation Lloyd, Seth, Silvano Garnerone, and Paolo Zanardi. “Quantum Algorithms for Topological and Geometric Analysis of Data.” Nat Comms 7 (January 25, 2016): 10138. As Published http://dx.doi.org/10.1038/ncomms10138 Publisher Nature Publishing Group Version Final published version Citable link http://hdl.handle.net/1721.1/101739 Terms of Use Creative Commons Attribution Detailed Terms http://creativecommons.org/licenses/by/4.0/ ARTICLE Received 17 Sep 2014 | Accepted 9 Nov 2015 | Published 25 Jan 2016 DOI: 10.1038/ncomms10138 OPEN Quantum algorithms for topological and geometric analysis of data Seth Lloyd1, Silvano Garnerone2 & Paolo Zanardi3 Extracting useful information from large data sets can be a daunting task. Topological methods for analysing data sets provide a powerful technique for extracting such information. Persistent homology is a sophisticated tool for identifying topological features and for determining how such features persist as the data is viewed at different scales. Here we present quantum machine learning algorithms for calculating Betti numbers—the numbers of connected components, holes and voids—in persistent homology, and for finding eigenvectors and eigenvalues of the combinatorial Laplacian. The algorithms provide an exponential speed-up over the best currently known classical algorithms for topological data analysis. 1 Department of Mechanical Engineering, Research Lab for Electronics, Massachusetts Institute of Technology, MIT 3-160, Cambridge, Massachusetts 02139, USA. 2 Institute for Quantum Computing, University of Waterloo, Waterloo, Ontario, Canada N2L 3G1.
    [Show full text]
  • The Topology of Data
    techniques. In the approximation that the vacuum density is just the volume form on moduli space, the surface area of the boundary will just be thesurfaceareaoftheboundary in moduli space. Taking the region R to be a sphere in moduli space of radius r,wefind A(S1) √K Developing Topological Observables V (S1) ∼ r so the condition Eq. (5.2) becomes K L> . (5.3) in Cosmology r2 Thus, if we consider a large enough region, or the entire moduli space in order to find the total number of vacua, the condition for the asymptotic vacuum counting formulas we have discussed in this work to hold is L>cKwith some order one coe∼cient. But if we Alex Cole subdivide the region into subregions which do not satisfy Eq.(5.3),wewillfindthatthe number of vacua in each subregion will show oscillations around this centralThe scaling. In Topology of Data:PhD Thesis Defense fact, most regions will contain a smaller number of vacua (like S above), while a few should ∼ August 12, 2020 have anomalously large numbers (like S above), averaging out toFrom Eq. (5.1). String Theory to Cosmology to Phases of Matter 5.1 Flux vacua on rigid Calabi-Yau As an illustration of this, consider the following toy problem with K =4,studiedin[1].Theconfiguration space is simply the fundamental region of the upper 3 half plane, parameterized by ∼.Thefluxsuperpoten- tials are taken to be W = A∼ + B with A = a1 + ia2 and B = b1 + ib2 each taking values 2 in Z+iZ.Thiswouldbeobtainedifweconsideredflux vacua on a rigid Calabi-Yau, with no complex structure moduli, b3 =2,andtheperiods√1 =1and√2 = i.
    [Show full text]
  • Arxiv:0811.1868V2 [Cs.CG]
    NECESSARY CONDITIONS FOR DISCONTINUITIES OF MULTIDIMENSIONAL SIZE FUNCTIONS A. CERRI AND P. FROSINI Abstract. Some new results about multidimensional Topological Persistence are presented, proving that the discontinuity points of a k-dimensional size function are necessarily related to the pseudocritical or special values of the associated measuring function. Introduction Topological Persistence is devoted to the study of stable properties of sublevel sets of topological spaces and, in the course of its development, has revealed itself to be a suitable framework when dealing with applications in the field of Shape Analysis and Comparison. Since the beginning of the 1990s research on this sub- ject has been carried out under the name of Size Theory, studying the concept of size function, a mathematical tool able to describe the qualitative properties of a shape in a quantitative way. More precisely, the main idea is to model a shape by a topological space endowed with a continuous function ϕ, called measuring function. Such a functionM is chosen according to applications and can be seen as a descriptor of the features considered relevant for shape characterization. Under these assumptions, the size function ℓ( ,ϕ) associated with the pair ( , ϕ) is a de- scriptor of the topological attributes thatM persist in the sublevel setsM of induced by the variation of ϕ. According to this approach, the problem of comparingM two shapes can be reduced to the simpler comparison of the related size functions. Since their introduction, these shape descriptors have been widely studied and applied in quite a lot of concrete applications concerning Shape Comparison and Pattern Recognition (cf., e.g., [4, 8, 15, 34, 35, 36]).
    [Show full text]