The Extremely High Dark Matter Halo Concentration of the Relic Compact
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-
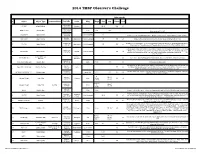
2014 Observers Challenge List
2014 TMSP Observer's Challenge Atlas page #s # Object Object Type Common Name RA, DEC Const Mag Mag.2 Size Sep. U2000 PSA 18h31m25s 1 IC 1287 Bright Nebula Scutum 20'.0 295 67 -10°47'45" 18h31m25s SAO 161569 Double Star 5.77 9.31 12.3” -10°47'45" Near center of IC 1287 18h33m28s NGC 6649 Open Cluster 8.9m Integrated 5' -10°24'10" Can be seen in 3/4d FOV with above. Brightest star is 13.2m. Approx 50 stars visible in Binos 18h28m 2 NGC 6633 Open Cluster Ophiuchus 4.6m integrated 27' 205 65 Visible in Binos and is about the size of a full Moon, brightest star is 7.6m +06°34' 17h46m18s 2x diameter of a full Moon. Try to view this cluster with your naked eye, binos, and a small scope. 3 IC 4665 Open Cluster Ophiuchus 4.2m Integrated 60' 203 65 +05º 43' Also check out “Tweedle-dee and Tweedle-dum to the east (IC 4756 and NGC 6633) A loose open cluster with a faint concentration of stars in a rich field, contains about 15-20 stars. 19h53m27s Brightest star is 9.8m, 5 stars 9-11m, remainder about 12-13m. This is a challenge obJect to 4 Harvard 20 Open Cluster Sagitta 7.7m integrated 6' 162 64 +18°19'12" improve your observation skills. Can you locate the miniature coathanger close by at 19h 37m 27s +19d? Constellation star Corona 5 Corona Borealis 55 Trace the 7 stars making up this constellation, observe and list the colors of each star asterism Borealis 15H 32' 55” Theta Corona Borealis Double Star 4.2m 6.6m .97” 55 Theta requires about 200x +31° 21' 32” The direction our Sun travels in our galaxy. -

7.5 X 11.5.Threelines.P65
Cambridge University Press 978-0-521-19267-5 - Observing and Cataloguing Nebulae and Star Clusters: From Herschel to Dreyer’s New General Catalogue Wolfgang Steinicke Index More information Name index The dates of birth and death, if available, for all 545 people (astronomers, telescope makers etc.) listed here are given. The data are mainly taken from the standard work Biographischer Index der Astronomie (Dick, Brüggenthies 2005). Some information has been added by the author (this especially concerns living twentieth-century astronomers). Members of the families of Dreyer, Lord Rosse and other astronomers (as mentioned in the text) are not listed. For obituaries see the references; compare also the compilations presented by Newcomb–Engelmann (Kempf 1911), Mädler (1873), Bode (1813) and Rudolf Wolf (1890). Markings: bold = portrait; underline = short biography. Abbe, Cleveland (1838–1916), 222–23, As-Sufi, Abd-al-Rahman (903–986), 164, 183, 229, 256, 271, 295, 338–42, 466 15–16, 167, 441–42, 446, 449–50, 455, 344, 346, 348, 360, 364, 367, 369, 393, Abell, George Ogden (1927–1983), 47, 475, 516 395, 395, 396–404, 406, 410, 415, 248 Austin, Edward P. (1843–1906), 6, 82, 423–24, 436, 441, 446, 448, 450, 455, Abbott, Francis Preserved (1799–1883), 335, 337, 446, 450 458–59, 461–63, 470, 477, 481, 483, 517–19 Auwers, Georg Friedrich Julius Arthur v. 505–11, 513–14, 517, 520, 526, 533, Abney, William (1843–1920), 360 (1838–1915), 7, 10, 12, 14–15, 26–27, 540–42, 548–61 Adams, John Couch (1819–1892), 122, 47, 50–51, 61, 65, 68–69, 88, 92–93, -

Binocular Challenges
This page intentionally left blank Cosmic Challenge Listing more than 500 sky targets, both near and far, in 187 challenges, this observing guide will test novice astronomers and advanced veterans alike. Its unique mix of Solar System and deep-sky targets will have observers hunting for the Apollo lunar landing sites, searching for satellites orbiting the outermost planets, and exploring hundreds of star clusters, nebulae, distant galaxies, and quasars. Each target object is accompanied by a rating indicating how difficult the object is to find, an in-depth visual description, an illustration showing how the object realistically looks, and a detailed finder chart to help you find each challenge quickly and effectively. The guide introduces objects often overlooked in other observing guides and features targets visible in a variety of conditions, from the inner city to the dark countryside. Challenges are provided for viewing by the naked eye, through binoculars, to the largest backyard telescopes. Philip S. Harrington is the author of eight previous books for the amateur astronomer, including Touring the Universe through Binoculars, Star Ware, and Star Watch. He is also a contributing editor for Astronomy magazine, where he has authored the magazine’s monthly “Binocular Universe” column and “Phil Harrington’s Challenge Objects,” a quarterly online column on Astronomy.com. He is an Adjunct Professor at Dowling College and Suffolk County Community College, New York, where he teaches courses in stellar and planetary astronomy. Cosmic Challenge The Ultimate Observing List for Amateurs PHILIP S. HARRINGTON CAMBRIDGE UNIVERSITY PRESS Cambridge, New York, Melbourne, Madrid, Cape Town, Singapore, Sao˜ Paulo, Delhi, Dubai, Tokyo, Mexico City Cambridge University Press The Edinburgh Building, Cambridge CB2 8RU, UK Published in the United States of America by Cambridge University Press, New York www.cambridge.org Information on this title: www.cambridge.org/9780521899369 C P. -

Making a Sky Atlas
Appendix A Making a Sky Atlas Although a number of very advanced sky atlases are now available in print, none is likely to be ideal for any given task. Published atlases will probably have too few or too many guide stars, too few or too many deep-sky objects plotted in them, wrong- size charts, etc. I found that with MegaStar I could design and make, specifically for my survey, a “just right” personalized atlas. My atlas consists of 108 charts, each about twenty square degrees in size, with guide stars down to magnitude 8.9. I used only the northernmost 78 charts, since I observed the sky only down to –35°. On the charts I plotted only the objects I wanted to observe. In addition I made enlargements of small, overcrowded areas (“quad charts”) as well as separate large-scale charts for the Virgo Galaxy Cluster, the latter with guide stars down to magnitude 11.4. I put the charts in plastic sheet protectors in a three-ring binder, taking them out and plac- ing them on my telescope mount’s clipboard as needed. To find an object I would use the 35 mm finder (except in the Virgo Cluster, where I used the 60 mm as the finder) to point the ensemble of telescopes at the indicated spot among the guide stars. If the object was not seen in the 35 mm, as it usually was not, I would then look in the larger telescopes. If the object was not immediately visible even in the primary telescope – a not uncommon occur- rence due to inexact initial pointing – I would then scan around for it. -

Ngc Catalogue Ngc Catalogue
NGC CATALOGUE NGC CATALOGUE 1 NGC CATALOGUE Object # Common Name Type Constellation Magnitude RA Dec NGC 1 - Galaxy Pegasus 12.9 00:07:16 27:42:32 NGC 2 - Galaxy Pegasus 14.2 00:07:17 27:40:43 NGC 3 - Galaxy Pisces 13.3 00:07:17 08:18:05 NGC 4 - Galaxy Pisces 15.8 00:07:24 08:22:26 NGC 5 - Galaxy Andromeda 13.3 00:07:49 35:21:46 NGC 6 NGC 20 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 7 - Galaxy Sculptor 13.9 00:08:21 -29:54:59 NGC 8 - Double Star Pegasus - 00:08:45 23:50:19 NGC 9 - Galaxy Pegasus 13.5 00:08:54 23:49:04 NGC 10 - Galaxy Sculptor 12.5 00:08:34 -33:51:28 NGC 11 - Galaxy Andromeda 13.7 00:08:42 37:26:53 NGC 12 - Galaxy Pisces 13.1 00:08:45 04:36:44 NGC 13 - Galaxy Andromeda 13.2 00:08:48 33:25:59 NGC 14 - Galaxy Pegasus 12.1 00:08:46 15:48:57 NGC 15 - Galaxy Pegasus 13.8 00:09:02 21:37:30 NGC 16 - Galaxy Pegasus 12.0 00:09:04 27:43:48 NGC 17 NGC 34 Galaxy Cetus 14.4 00:11:07 -12:06:28 NGC 18 - Double Star Pegasus - 00:09:23 27:43:56 NGC 19 - Galaxy Andromeda 13.3 00:10:41 32:58:58 NGC 20 See NGC 6 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 21 NGC 29 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 22 - Galaxy Pegasus 13.6 00:09:48 27:49:58 NGC 23 - Galaxy Pegasus 12.0 00:09:53 25:55:26 NGC 24 - Galaxy Sculptor 11.6 00:09:56 -24:57:52 NGC 25 - Galaxy Phoenix 13.0 00:09:59 -57:01:13 NGC 26 - Galaxy Pegasus 12.9 00:10:26 25:49:56 NGC 27 - Galaxy Andromeda 13.5 00:10:33 28:59:49 NGC 28 - Galaxy Phoenix 13.8 00:10:25 -56:59:20 NGC 29 See NGC 21 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 30 - Double Star Pegasus - 00:10:51 21:58:39 -

QUANTUM GRAVITY and the ROLE of CONSCIOUSNESS in PHYSICS Resolving the Contradictions Between Quantum Mechanics and Relativity
1 QUANTUM CONSCIOUSNESS RESEARCH LIMITED QUANTUM GRAVITY and the ROLE of CONSCIOUSNESS in PHYSICS Resolving the contradictions between quantum mechanics and relativity Sky Darmos 2020/8/14 Explains/resolves accelerated expansion, quantum entanglement, information paradox, flatness problem, consciousness, non-Copernican structures, quasicrystals, dark matter, the nature of quantum spin, weakness of gravity, arrow of time, vacuum paradox, and much more. 2 Working titles: Physics of the Mind (2003 - 2006); The Conscious Universe (2013 - 2014). Presented theories (created and developed by Sky Darmos): Similar-worlds interpretation (2003); Space particle dualism theory* (2005); Conscious set theory (2004) (Created by the author independently but fundamentally dependent upon each other). *Inspired by Roger Penrose’s twistor theory (1967). Old names of these theories: Equivalence theory (2003); Discontinuity theory (2005); Relationism (2004). Contact information: Facebook: Sky Darmos WeChat: Sky_Darmos Email: [email protected] Cover design: Sky Darmos (2005) Its meaning: The German word “Elementarräume”, meaning elementary spaces, is written in graffiti style. The blue background looks like a 2-dimensional surface, but when we look at it through the two magnifying glasses at the bottom we see that it consists of 1-dimensional elementary “spaces” (circles). That is expressing the idea that our well known 3-dimensional space could in the same way be made of 2- dimensional sphere surfaces. The play with dimensionality is further extended by letting all the letters approach from a distant background where they appear as a single point (or point particle) moving through the pattern formed by these overlapping elementary spaces. The many circles originating from all angles in the letters represent the idea that every point (particle) gives rise to another elementary space (circle). -

Jrasc Dec 1998
Publications from December/décembre 1998 Volume/volume 92 Number/numero 6 [674] The Royal Astronomical Society of Canada NEW LARGER SIZE! Observer’s Calendar — 1999 This calendar was created by members of the RASC. All photographs were taken by amateur astronomers using ordinary camera lenses and small The Journal of the Royal Astronomical Society of Canada Le Journal de la Société royale d’astronomie du Canada telescopes and represent a wide spectrum of objects. An informative caption accompanies every photograph. This year all of the photos are in full colour. It is designed with the observer in mind and contains comprehensive astronomical data such as daily Moon rise and set times, significant lunar and planetary conjunctions, eclipses, and meteor showers. (designed and produced by Rajiv Gupta) Price: $14 (includes taxes, postage and handling) The Beginner’s Observing Guide This guide is for anyone with little or no experience in observing the night sky. Large, easy to read star maps are provided to acquaint the reader with the constellations and bright stars. Basic information on observing the moon, planets and eclipses through the year 2000 is provided. There is also a special section to help Scouts, Cubs, Guides and Brownies achieve their respective astronomy badges. Written by Leo Enright (160 pages of information in a soft-cover book with a spiral binding which allows the book to lie flat). Price: $12 (includes taxes, postage and handling) Looking Up: A History of the Royal Astronomical Society of Canada Published to commemorate the 125th anniversary of the first meeting of the Toronto Astronomical Club, “Looking Up — A History of the RASC” is an excellent overall history of Canada’s national astronomy organization. -

Kayhan Gultekin's CV
Kayhan Gültekin’s Curriculum Vitae Kayhan Gültekin E-mail: [email protected] The University of Michigan Tel: +1 734 255 7082 Department of Astronomy Fax: +1 734 763 6317 403 West Hall Web: www.umich.edu/˜kayhan 1085 S. University Ann Arbor, MI 48109 Nationality: Dual US & Turkish Education August 2006 PhD, Astronomy University of Maryland, College Park, MD, USA Thesis: “Growing IMBHs with Gravitational Waves” Adviser: M. Coleman Miller December 2001 MS, Astronomy University of Maryland, College Park, MD, USA May 1999 BA, Physics University of Pennsylvania, Philadelphia, PA, USA with distinction Thesis: “A Circumstellar Disk Around the High-Mass Pro- tostar L1206A” Adviser: David W. Koerner Research Interests • Understanding the interface of supermassive black holes (SMBHs) and galaxies. What does a galaxy need to do to feed a black hole efficiently? How effectively can a black hole influence its host galaxy? • Observational studies of SMBHs as a population with respect to their host galaxies. Multi-wavelength observations with cutting edge instrumentation and numerical models to identify SMBHs, measure their masses, and catalog their demographics to understand their formation, evolution, and role in galaxy evolu- tion. • Observational search for and theoretical predictions of binary black holes. Develop search strategies to find compact supermassive black-hole binaries based on predictions by analytical and computational models. • Observational and analytical modeling of accretion onto the smallest AGNs. Build undersanding of how accretion and outflows work in general by investigating how they work in the lowest mass black holes. I do this through multi-wavelength observations to construct the spectral energy distribution (SED) of AGNs known to have low-mass black holes. -
Karl Gebhardt Mail Addresses Personal Data Education Research Experience Honors and Awards
Karl Gebhardt Herman and Joan Suit Professor of Astrophysics Mail Addresses University of Texas at Austin Residence: Astronomy Department 1808 Burbank Str 1UniversityStationC1400 Austin,TX78757 Austin, TX 78712-0259 Phone: (512)–471–1473 Fax: (512)–471–6016 Email: [email protected] URL: http://hoku.as.utexas.edu/∼gebhardt/ Personal Data Birth: Easton, PA, Aug. 19, 1964 Current Status: Professor Education 1994, Ph.D. in Physics and Astronomy, Rutgers University. 1990, M.S. Physics and Astronomy, Michigan State University, East Lansing, MI. 1986, B.S. Physics and Astronomy, University of Rochester, Rochester, NY. Research Experience 2006 – present Professor, University of Texas at Austin 2006 – present Project Scientist, Hobby-Eberly Telescope Dark Energy Experiment 2005 – 2010 Visiting Professor, Max-Planck-Institut fuer Extraterrestrische Physik 2004 – 2006 Associate Professor, University of Texas at Austin 2000 – 2004 Assistant Professor, University of Texas at Austin 1997 – 2000 Hubble Fellow, University of California, Santa Cruz 1994 – 1997 Postdoctoral research, University of Michigan 1991 – 1994 Ph.D. research with Dr. C. Pryor and Dr. T.B. Williams 1987 – 1991 M.S. research with Dr. T.C. Beers at Michigan State University Honors and Awards 2016 Rutgers Distinguised Fellows, 250th Anniversary 2014 College of Natural Science Outreach Award 2012 Edith and Peter O’DonnellAward in Science from the Academy of Medicine, Engineering and Science of Texas 2009 Herman and Joan Suit Professor of Astrophysics 2004 NSFCAREERAward 2004 Teaching Excellence Award, McDonald Board of Visitors 2003 Teaching Excellence Award, University of Texas 2003 Benjamin Dean Lecturer, Morrison Planetarium 2001 Invited talk at American Astronomical Society Meeting 1997 – 2000 Hubble Fellowship Karl Gebhardt October 17, 2016 1995 Recipient of the 1995 Northeastern Association of Graduate Schools Dissertation Award (2 per year in Science) 1991 – 1993 U.S. -
Based on Space Particle Dualism Theory
Academia Journal of Scientific Research 8(10): 290-319, October 2020 DOI: 10.15413/ajsr.2020.0124 ISSN 2315-7712 ©2020 Academia Publishing Research Paper Entropic expansion and the true age of the universe – based on space particle dualism theory Accepted 11th June, 2020 ABSTRACT Space particle dualism theory (SPD) is an overarching quantum theory of gravity, created and developed by the author in 2005. It is the first approach to quantum gravity which does not use Planck size entities as building blocks for space. Instead each particle carries a quantum of space which is a complex 2-sphere with a radius of 푅 with SPD is also the only approach to quantum gravity which doesn’t predict gravitons. In fact it does away with 푚1 푚2 conventional gravity all together, Newton’s famous law of gravity 퐹 = 퐺 is replaced by with and being the number of quarks 푛q1 and 푛q2 in two gravitational bodies. The principle behind this is that in SPD space is made of overlapping complex 2-spheres with a granular dimensionality, with 푛 denoting the number of connections from one elementary space to other elementary spaces (or surfaces). Charged particles emit virtual gauge bosons which carry their own elementary spaces That results in a higher granular dimensionality 퐷퐺 , with 푛 and a higher vacuum connectivity 푛퐸 around charged particles. More pathways lead through such charge containing regions of space. The various experimentally confirmed effects of special and general relativity can be explained using uniformly growing elementary spaces (SR) and uniformly changing granular dimensionality (GR). The fact that, unlike GR, in SPD gravity depends on density differences, and not on absolute values of mass or energy, the vacuum catastrophe is avoided and the flatness problem is solved. -

Per – Objektauswahl NGC
Per – Objektauswahl NGC NGC 0650 NGC 1039 NGC 1131 NGC 1177 NGC 1227 NGC 1270 NGC 1282 NGC 1465 NGC 1605 NGC 0651 NGC 1050 NGC 1138 NGC 1186 NGC 1233 NGC 1271 NGC 1283 NGC 1491 NGC 1624 NGC 0744 NGC 1053 NGC 1159 NGC 1193 NGC 1245 NGC 1272 NGC 1293 NGC 1496 NGC 0869 NGC 1058 NGC 1160 NGC 1198 NGC 1250 NGC 1273 NGC 1294 NGC 1499 NGC 0884 NGC 1077 NGC 1161 NGC 1207 NGC 1259 NGC 1274 NGC 1333 NGC 1513 NGC 0957 NGC 1086 NGC 1164 NGC 1212 NGC 1260 NGC 1275 NGC 1334 NGC 1528 NGC 1001 NGC 1106 NGC 1167 NGC 1213 NGC 1264 NGC 1277 NGC 1335 NGC 1545 NGC 1003 NGC 1122 NGC 1169 NGC 1220 NGC 1265 NGC 1278 NGC 1342 NGC 1548 NGC 1005 NGC 1129 NGC 1171 NGC 1224 NGC 1267 NGC 1279 NGC 1348 NGC 1579 NGC 1023 NGC 1130 NGC 1175 NGC 1226 NGC 1268 NGC 1281 NGC 1444 NGC 1582 Sternbild- Zur Objektauswahl: Nummer anklicken Übersicht Zur Übersichtskarte: Objekt in Aufsuchkarte anklicken Zum Detailfoto: Objekt in Übersichtskarte anklicken Übersichtskarte Auswahl NGC 650_651 Aufsuchkarte Auswahl Auswahl NGC 650_651 ÜbersichtskarteNGC Aufsuch- karte NGC 744 Aufsuchkarte Auswahl Auswahl NGC 744 ÜbersichtskarteNGC Aufsuch- karte NGC 869_884_957 Aufsuchkarte Auswahl Auswahl NGC 869_884 ÜbersichtskarteNGC Aufsuch- karte Auswahl NGC 957 ÜbersichtskarteNGC Aufsuch- karte N1001_3_5_39_53_77_86_1106_22_29_30_31_38 Aufsuchkarte Auswahl Auswahl NGC 1001_1005_1053 ÜbersichtskarteNGC Aufsuch- karte Auswahl NGC 1003 ÜbersichtskarteNGC Aufsuch- karte Auswahl NGC 1039 ÜbersichtskarteNGC Aufsuch- karte Auswahl NGC 1077 ÜbersichtskarteNGC Aufsuch- karte Auswahl NGC 1086 ÜbersichtskarteNGC -

JONELLE L. WALSH Department of Physics & Astronomy Texas A&M University 4242 TAMU, College Station, TX 77843-4242 E-Mail: [email protected]
JONELLE L. WALSH Department of Physics & Astronomy Texas A&M University 4242 TAMU, College Station, TX 77843-4242 E-mail: [email protected] RESEARCH INTERESTS Supermassive black holes in nearby galaxy nuclei • Black hole – galaxy relationships • Galaxy kinematics and dynamics • Reverberation mapping and AGN variability • Adaptive optics observations EDUCATION Ph.D., Physics and Astronomy, University of California, Irvine June 2011 M.S., Physics and Astronomy, University of California, Irvine Sept 2007 B.A., Physics with Honors, Economics Minor, Bowdoin College May 2005 POSITIONS HELD Assistant Professor, Texas A&M University 2017 – present Mitchell Postdoctoral Fellow in Astronomy, Texas A&M University 2014 – 2017 NSF Astronomy & Astrophysics Postdoctoral Fellow, University of Texas at Austin 2011 – 2014 Graduate Student Researcher, University of California, Irvine 2006 – 2011 OBSERVING EXPERIENCE AWARDED TELESCOPE TIME AS PI/LEAD SCIENCE PI 1 Gemini Large and Long Program 2016 – 2019 253 hrs 3 ALMA proposals 2016 – 2018 9.9 hrs 1 HST (WFC3) proposal 2017 25 orbits 9 Keck (OSIRIS, LRIS) proposals† 2009 – 2014 9.5 nights 3 Gemini (NIFS) proposals 2012 – 2013 20.5 hrs 3 McDonald 2.7m (VIRUS-P, VIRUS-W) proposals 2013, 2018 13 nights AWARDED TELESCOPE TIME AS CO-I 9 HST (STIS, WFC3, ACS) proposals 2010 – 2014, 2016 – 2017 70 orbits 7 ALMA proposals 2014 – 2018 38.2 hrs 7 McDonald 2.7m (VIRUS-P, VIRUS-W) proposals 2015 – 2017 40 nights 6 HET (LRS, LRS2) proposals 2012 – 2017 132 hrs 5 Keck (OSIRIS, LRIS) proposals† 2009 – 2011, 2014, 2016 5 nights 1 Chandra + VLA proposal 2014 123 ksec + 21 hrs 2 VLT (SINFONI) proposals 2011 – 2012 19 hrs † time awarded through NOAO and UC 1 PUBLICATION SUMMARY 42 papers (8 first author) in peer-reviewed journals, including ApJ, ApJL, ApJS, AJ, MNRAS, and Nature.