Fundamentals of LHC Experiments
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

NRP-3 the Effect of Beryllium Interaction with Fast Neutrons on the Reactivity of Etrr-2 Research Reactor
Seventh Conference of Nuclear Sciences & Applications 6-10 February 2000, Cairo, Egypt NRP-3 The Effect Of Beryllium Interaction With Fast Neutrons On the Reactivity Of Etrr-2 Research Reactor Moustafa Aziz and A.M. EL Messiry National Center for Nuclear Safety Atomic Energy Autho , Cairo , Egypt ABSTRACT The effect of beryllium interactions with fast neutrons is studied for Etrr_2 research reactors. Isotope build up inside beryllium blocks is calculated under different irradiation times. A new model for the Etrr_2 research reactor is designed using MCNP code to calculate the reactivity and flux change of the reactor due to beryllium poison. Key words: Research Reactors , Neutron Flux , Beryllium Blocks, Fast Neutrons and Reactivity INTRODUCTION Beryllium irradiated by fast neutrons with energies in the range 0.7-20 Mev undergoes (n,a) and (n,2n) reactions resulting in subsequent formation of the isotopes lithium (Li-6), tritium (H-3) and helium (He-3 and He-4 ). Beryllium interacts with fast neutrons to produce 6He that decay 6 6 ( T!/2 =0.8 s) to produce Li . Li interacts with neutron to produce tritium which suffer /? (T1/2 = 12.35 year) decay and converts to 3He which finally interact with neutron to produce tritium. These processes some times defined as Beryllium poison. Negative effect of this process are met whenever beryllium is used in a thermal reactor as a reflector or moderator . Because of their large thermal neutron absorption cross sections , the buildup of He-3 and Li-6 concentrations ,initiated by the Be(n,a) reaction , results in large negative reactivities which alter the reactivity , flux and power distributions. -

From Precision Physics to the Energy Frontier with the Compact Linear Collider
PERSPECTIVE | FOCUS https://doi.org/10.1038/s41567-020-0834-8PERSPECTIVE | FOCUS From precision physics to the energy frontier with the Compact Linear Collider Eva Sicking ✉ and Rickard Ström The Compact Linear Collider (CLIC) is a proposed high-luminosity collider that would collide electrons with their antiparticles, positrons, at energies ranging from a few hundred giga-electronvolts to a few tera-electronvolts. By covering a large energy range and by ultimately reaching collision energies in the multi-tera-electronvolts range, scientists at CLIC aim to improve the understanding of nature’s fundamental building blocks and to discover new particles or other physics phenomena. CLIC is an international project hosted by CERN with 75 institutes worldwide participating in the accelerator, detector and physics stud- ies. If commissioned, the first electron–positron collisions at CLIC are expected around 2035, following the high-luminosity phase of the Large Hadron Collider at CERN. Here we survey the principal merits of CLIC, and examine the opportunities that arise as a result of its design. We argue that CLIC represents an attractive proposition for the next-generation particle col- lider by combining an innovative accelerator technology, a realistic delivery timescale, and a physics programme that is highly complementary to existing accelerators, reaching uncharted territory. he discovery of the Higgs boson at the Large Hadron Collider to a lower event rate. These characteristics and the low duty cycle (LHC) in 20121,2 was an important milestone in high-energy of linear colliders make a trigger-less detector readout possible at Tphysics. It completes a puzzle that scientists have been work- CLIC. -

Il Nostro Mondo
IL NOSTRO MONDO THE DESIGN, CONSTRUCTION AND PERFORMANCE OF THE CERN INTERSECTING STORAGE RINGS (ISR) A RECOLLECTION OF WORLD’S FIRST PROTON-PROTON COLLIDER KURT HÜBNER CERN, Geneva, Switzerland 1 Design which had a beam energy of 160 MeV. The interaction points to increase the collision rate The concept of colliding beams appeared design of these colliders started in 1957. but without special lattice insertions as one first in a German patent by Rolf Widerøe In 1961, the Accelerator Research Group would use these days. registered in 1943 and published in 1952. Division was expanded into the Accelerator Combined-function magnets were chosen However, at that time the intensity of beams Division as experienced manpower had as in the PS, i.e. the main magnets had a was too low for an exploitable collision rate as become available after the running-in of the magnetic dipole field to bend the beam and a beam accumulation had not yet been invented. PS in 1960. At the same time it was decided quadrupole field to focus the beam. This type The first ideas of a realistic design were to construct a small accelerator to test rf of magnet provided space for the elaborate published in 1956 by Gerard O’Neill and by the stacking, a technique to be experimentally pole-face windings foreseen to control the MURA Group lead by Donald Kerst in the USA. proven, as it was essential for the performance magnetic field to a very high precision. It also MURA had come up with beam accumulation and success of the ISR. -

Hadron Collider Physics
KEK-PH Lectures and Workshops Hadron Collider Physics Zhen Liu University of Maryland 08/05/2020 Part I: Basics Part II: Advanced Topics Focus Collider Physics is a vast topic, one of the most systematically explored areas in particle physics, concerning many observational aspects in the microscopic world • Focus on important hadron collider concepts and representative examples • Details can be studied later when encounter References: Focus on basic pictures Barger & Philips, Collider Physics Pros: help build intuition Tao Han, TASI lecture, hep-ph/0508097 Tilman Plehn, TASI lecture, 0910.4182 Pros: easy to understand Maxim Perelstein, TASI lecture, 1002.0274 Cons: devils in the details Particle Data Group (PDG) and lots of good lectures (with details) from CTEQ summer schools Zhen Liu Hadron Collider Physics (lecture) KEK 2020 2 Part I: Basics The Large Hadron Collider Lyndon R Evans DOI:10.1098/rsta.2011.0453 Path to discovery 1995 1969 1974 1969 1979 1969 1800-1900 1977 2012 2000 1975 1983 1983 1937 1962 Electric field to accelerate 1897 1956 charged particles Synchrotron radiation 4 Zhen Liu Hadron Collider Physics (lecture) KEK 2020 4 Zhen Liu Hadron Collider Physics (lecture) KEK 2020 5 Why study (hadron) colliders (now)? • Leading tool in probing microscopic structure of nature • history of discovery • Currently running LHC • Great path forward • Precision QFT including strong dynamics and weakly coupled theories • Application to other physics probes • Set-up the basic knowledge to build other subfield of elementary particle physics Zhen Liu Hadron Collider Physics (lecture) KEK 2020 6 Basics: Experiment & Theory Zhen Liu Hadron Collider Physics (lecture) KEK 2020 7 Basics: How to make measurements? Zhen Liu Hadron Collider Physics (lecture) KEK 2020 8 Part I: Basics Basic Parameters Basics: Smashing Protons & Quick Estimates Proton Size ( ) Proton-Proton cross section ( ) Particle Physicists use the unit “Barn”2 1 = 100 The American idiom "couldn't hit the broad side of a barn" refers to someone whose aim is very bad. -

HEPAP Looks Into the Future
Volume 20 Friday, August 29, 1997 Number 17 f INSIDE HEPAP Looks into 2 HEPAP: Voice of the Community the Future 5 Profiles in HEPAP subpanel meets at Fermilab to chart the future of Particle Physics: high-energy physics in the U.S. Dave McGinnis by Donald Sena and Sharon Butler, Office of Public Affairs 6 Barns of Fermilab Charged with recommending how best to In a letter to HEPAP, Martha Krebs, position the U.S. particle physics community Director of the U.S. Department of Energy’s for new facilities beyond CERN’s Large Office of Energy Research, directed the Hadron Collider, a subpanel of the High- subpanel to “recommend a scenario for an Energy Physics Advisory Panel met at Fermilab optimal and balanced U.S. high-energy physics August 14-16 to hear presentations on such program over the next decade,” with “new topics as the research agenda for Fermilab’s facilities to address physics opportunities Run II, the complicated upgrades to the CDF beyond the LHC.” She asked the subpanel and DZero detectors and research on future to consider a future course in light of three accelerators. continued on page 3 Photo by Reidar Hahn Dixon Bogert, deputy project manager for the Main Injector, leads a tour for HEPAP subpanel members and DOE officials. HEPAP: Voice of the Community by Donald Sena and Sharon Butler, Office of Public Affairs The High-Energy Physics Advisory In 1983, for example, a HEPAP According to Fermilab physicist Cathy Panel traces its history to the 1960s, subpanel recommended terminating Newman-Holmes, outgoing member of when -

Pos(ICRC2019)446
New Results from the Cosmic-Ray Program of the NA61/SHINE facility at the CERN SPS PoS(ICRC2019)446 Michael Unger∗ for the NA61/SHINE Collaborationy Karlsruhe Institute of Technology (KIT), Postfach 3640, D-76021 Karlsruhe, Germany E-mail: [email protected] The NA61/SHINE experiment at the SPS accelerator at CERN is a unique facility for the study of hadronic interactions at fixed target energies. The data collected with NA61/SHINE is relevant for a broad range of topics in cosmic-ray physics including ultrahigh-energy air showers and the production of secondary nuclei and anti-particles in the Galaxy. Here we present an update of the measurement of the momentum spectra of anti-protons produced in p−+C interactions at 158 and 350 GeV=c and discuss their relevance for the understanding of muons in air showers initiated by ultrahigh-energy cosmic rays. Furthermore, we report the first results from a three-day pilot run aimed at investigating the ca- pability of our experiment to measure nuclear fragmentation cross sections for the understanding of the propagation of cosmic rays in the Galaxy. We present a preliminary measurement of the production cross section of Boron in C+p interactions at 13.5 AGeV=c and discuss prospects for future data taking to provide the comprehensive and accurate reaction database of nuclear frag- mentation needed in the era of high-precision measurements of Galactic cosmic rays. 36th International Cosmic Ray Conference -ICRC2019- July 24th - August 1st, 2019 Madison, WI, U.S.A. ∗Speaker. yhttp://shine.web.cern.ch/content/author-list c Copyright owned by the author(s) under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND 4.0). -

Searches for a Charged Higgs Boson in ATLAS and Development of Novel Technology for Future Particle Detector Systems
Digital Comprehensive Summaries of Uppsala Dissertations from the Faculty of Science and Technology 1222 Searches for a Charged Higgs Boson in ATLAS and Development of Novel Technology for Future Particle Detector Systems DANIEL PELIKAN ACTA UNIVERSITATIS UPSALIENSIS ISSN 1651-6214 ISBN 978-91-554-9153-6 UPPSALA urn:nbn:se:uu:diva-242491 2015 Dissertation presented at Uppsala University to be publicly examined in Polhemssalen, Ångströmlaboratoriet, Lägerhyddsvägen 1, Uppsala, Friday, 20 March 2015 at 10:00 for the degree of Doctor of Philosophy. The examination will be conducted in English. Faculty examiner: Prof. Dr. Fabrizio Palla (Istituto Nazionale di Fisica Nucleare (INFN) Pisa). Abstract Pelikan, D. 2015. Searches for a Charged Higgs Boson in ATLAS and Development of Novel Technology for Future Particle Detector Systems. Digital Comprehensive Summaries of Uppsala Dissertations from the Faculty of Science and Technology 1222. 119 pp. Uppsala: Acta Universitatis Upsaliensis. ISBN 978-91-554-9153-6. The discovery of a charged Higgs boson (H±) would be a clear indication for physics beyond the Standard Model. This thesis describes searches for charged Higgs bosons with the ATLAS experiment at CERN’s Large Hadron Collider (LHC). The first data collected during the LHC Run 1 is analysed, searching for a light charged Higgs boson (mH±<mtop), which decays predominantly into a tau-lepton and a neutrino. Different final states with one or two leptons (electrons or muons), as well as leptonically or hadronically decaying taus, are studied, and exclusion limits are set. The background arising from misidentified non-prompt electrons and muons was estimated from data. This so-called "Matrix Method'' exploits the difference in the lepton identification between real, prompt, and misidentified or non-prompt electrons and muons. -

NA61/SHINE Facility at the CERN SPS: Beams and Detector System
Preprint typeset in JINST style - HYPER VERSION NA61/SHINE facility at the CERN SPS: beams and detector system N. Abgrall11, O. Andreeva16, A. Aduszkiewicz23, Y. Ali6, T. Anticic26, N. Antoniou1, B. Baatar7, F. Bay27, A. Blondel11, J. Blumer13, M. Bogomilov19, M. Bogusz24, A. Bravar11, J. Brzychczyk6, S. A. Bunyatov7, P. Christakoglou1, T. Czopowicz24, N. Davis1, S. Debieux11, H. Dembinski13, F. Diakonos1, S. Di Luise27, W. Dominik23, T. Drozhzhova20 J. Dumarchez18, K. Dynowski24, R. Engel13, I. Efthymiopoulos10, A. Ereditato4, A. Fabich10, G. A. Feofilov20, Z. Fodor5, A. Fulop5, M. Ga´zdzicki9;15, M. Golubeva16, K. Grebieszkow24, A. Grzeszczuk14, F. Guber16, A. Haesler11, T. Hasegawa21, M. Hierholzer4, R. Idczak25, S. Igolkin20, A. Ivashkin16, D. Jokovic2, K. Kadija26, A. Kapoyannis1, E. Kaptur14, D. Kielczewska23, M. Kirejczyk23, J. Kisiel14, T. Kiss5, S. Kleinfelder12, T. Kobayashi21, V. I. Kolesnikov7, D. Kolev19, V. P. Kondratiev20, A. Korzenev11, P. Koversarski25, S. Kowalski14, A. Krasnoperov7, A. Kurepin16, D. Larsen6, A. Laszlo5, V. V. Lyubushkin7, M. Mackowiak-Pawłowska´ 9, Z. Majka6, B. Maksiak24, A. I. Malakhov7, D. Maletic2, D. Manglunki10, D. Manic2, A. Marchionni27, A. Marcinek6, V. Marin16, K. Marton5, H.-J.Mathes13, T. Matulewicz23, V. Matveev7;16, G. L. Melkumov7, M. Messina4, St. Mrówczynski´ 15, S. Murphy11, T. Nakadaira21, M. Nirkko4, K. Nishikawa21, T. Palczewski22, G. Palla5, A. D. Panagiotou1, T. Paul17, W. Peryt24;∗, O. Petukhov16 C.Pistillo4 R. Płaneta6, J. Pluta24, B. A. Popov7;18, M. Posiadala23, S. Puławski14, J. Puzovic2, W. Rauch8, M. Ravonel11, A. Redij4, R. Renfordt9, E. Richter-Wa¸s6, A. Robert18, D. Röhrich3, E. Rondio22, B. Rossi4, M. Roth13, A. Rubbia27, A. Rustamov9, M. -
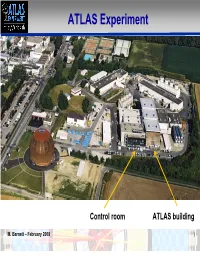
ATLAS Experiment
ATLAS Experiment Control room ATLAS building M. Barnett – February 2008 1 Final piece of ATLAS lowered last Friday (the second small muon wheel) M. Barnett – February 2008 2 M. Barnett – February 2008 3 Still to be done Connecting: Cables, Fibers, Cryogenics M. Barnett – February 2008 4 Celebrations M. Barnett – February 2008 5 News Coverage News media are flooding CERN well in advance of startup "Particle physics is the unbelievable in pursuit of the unimaginable. To pinpoint the smallest fragments of the universe you have to build the biggest machine in the world. To recreate the first millionths of a second of creation you have to focus energy on an awesome scale." The Guardian M. Barnett – February 2008 6 Three full pages in New York Times M. Barnett – February 2008 7 New York Times M. Barnett – February 2008 8 National Geographic Magazine M. Barnett – February 2008 9 National Geographic Magazine M. Barnett – February 2008 10 National Geographic Magazine M. Barnett – February 2008 11 M. Barnett – February 2008 12 M. Barnett – February 2008 13 M. Barnett – February 2008 14 M. Barnett – February 2008 15 M. Barnett – February 2008 16 M. Barnett – February 2008 17 M. Barnett – February 2008 18 M. Barnett – February 2008 19 M. Barnett – February 2008 20 M. Barnett – February 2008 21 M. Barnett – February 2008 22 And on television (shortened version) M. Barnett – February 2008 23 An ATLAS expert explains the Higgs evidence to a layperson. M. Barnett – February 2008 24 US-LHC Student Journalism Program April 2-7, 2008 (overlapping Open Days) Six teams of high school students (3 students/1 teacher) are going to CERN to report on the LHC startup. -

How and Why to Go Beyond the Discovery of the Higgs Boson
How and Why to go Beyond the Discovery of the Higgs Boson John Alison University of Chicago http://hep.uchicago.edu/~johnda/ComptonLectures.html Lecture Outline April 1st: Newton’s dream & 20th Century Revolution April 8th: Mission Barely Possible: QM + SR April 15th: The Standard Model April 22nd: Importance of the Higgs April 29th: Guest Lecture May 6th: The Cannon and the Camera May 13th: The Discovery of the Higgs Boson May 20th: Problems with the Standard Model May 27th: Memorial Day: No Lecture June 3rd: Going beyond the Higgs: What comes next ? 2 Reminder: The Standard Model Description fundamental constituents of Universe and their interactions Triumph of the 20th century Quantum Field Theory: Combines principles of Q.M. & Relativity Constituents (Matter Particles) Spin = 1/2 Leptons: Quarks: νe νµ ντ u c t ( e ) ( µ) ( τ ) ( d ) ( s ) (b ) Interactions Dictated by principles of symmetry Spin = 1 QFT ⇒ Particle associated w/each interaction (Force Carriers) γ W Z g Consistent theory of electromagnetic, weak and strong forces ... ... provided massless Matter and Force Carriers Serious problem: matter and W, Z carriers have Mass ! 3 Last Time: The Higgs Feild New field (Higgs Field) added to the theory Allows massive particles while preserve mathematical consistency Works using trick: “Spontaneously Symmetry Breaking” Zero Field value Symmetric in Potential Energy not minimum Field value of Higgs Field Ground State 0 Higgs Field Value Ground state (vacuum of Universe) filled will Higgs field Leads to particle masses: Energy cost to displace Higgs Field / E=mc 2 Additional particle predicted by the theory. Higgs boson: H Spin = 0 4 Last Time: The Higgs Boson What do we know about the Higgs Particle: A Lot Higgs is excitations of v-condensate ⇒ Couples to matter / W/Z just like v X matter: e µ τ / quarks W/Z h h ~ (mass of matter) ~ (mass of W or Z) matter W/Z Spin: 0 1/2 1 3/2 2 Only thing we don’t (didn’t!) know is the value of mH 5 History of Prediction and Discovery Late 60s: Standard Model takes modern form. -

Improving the Slow Extraction Efficiency of the CERN Super
Improving the slow extraction efficiency of the CERN Super Proton Synchrotron Brunner Kristóf Faculty of Science Eötvös Loránd University Supervisors: Barna Dániel, Wigner RCP Christoph Wiesner, CERN May 2018 Contents 1 Introduction4 2 CERN accelerator complex5 2.1 Accelerators..................................... 5 2.2 Experiments..................................... 6 2.2.1 Colliders .................................. 7 2.2.2 Fixed target experiments.......................... 7 2.3 Current and future demands of fixed target experiments.............. 7 3 Introduction to accelerator physics9 3.1 History of linear and circular accelerators ..................... 9 3.2 Design orbit, focusing................................. 11 3.3 Betatron oscillation, the behaviour of single particles ................ 11 3.4 The Twiss-ellipse, the behaviour of the beam ................... 13 3.5 Normalised phase space............................... 15 3.6 Tune and resonances ................................ 16 4 Extraction from a synchrotron 19 4.1 Fast extraction.................................... 19 4.2 Multi-turn extraction ................................ 20 4.3 Sextupole driven slow extraction........................... 21 4.4 Possible enhancements............................... 24 4.4.1 Diffuser................................... 24 4.4.2 Dynamic bump............................... 26 4.4.3 Phase space folding............................. 26 5 Massless septum 28 5.1 Method of phase space folding using a massless septum.............. 29 6 Simulation -

Nuclear Criticality Safety Engineer Training Module 1 1
Nuclear Criticality Safety Engineer Training Module 1 1 Introductory Nuclear Criticality Physics LESSON OBJECTIVES 1) to introduce some background concepts to engineers and scientists who do not have an educational background in nuclear engineering, including the basic ideas of moles, atom densities, cross sections and nuclear energy release; 2) to discuss the concepts and mechanics of nuclear fission and the definitions of fissile and fissionable nuclides. NUCLEAR CRITICALITY SAFETY The American National Standard for Nuclear Criticality Safety in Operations with Fissionable Materials Outside Reactors, ANSI/ANS-8.1 includes the following definition: Nuclear Criticality Safety: Protection against the consequences of an inadvertent nuclear chain reaction, preferably by prevention of the reaction. Note the words: nuclear - related to the atomic nucleus; criticality - can it be controlled, will it run by itself; safety - protection of life and property. DEFINITIONS AND NUMBERS What is energy? Energy is the ability to do work. What is nuclear energy? Energy produced by a nuclear reaction. What is work? Work is force times distance. 1 Developed for the U. S. Department of Energy Nuclear Criticality Safety Program by T. G. Williamson, Ph.D., Westinghouse Safety Management Solutions, Inc., in conjunction with the DOE Criticality Safety Support Group. NCSET Module 1 Introductory Nuclear Criticality Physics 1 of 18 Push a car (force) along a road (distance) and the car has energy of motion, or kinetic energy. Climb (force) a flight of steps (distance) and you have energy of position relative to the first step, or potential energy. Jump down the stairs or out of a window and the potential energy is changed to kinetic energy as you fall.