DOCSLIB.ORG

R: a Free Software Project in Statistical Computing

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
R: a Free Software Project in Statistical Computing R: A Free Software Project in Statistical Computing Achim Zeileis http://statmath.wu-wien.ac.at/∼zeileis/ [email protected] Overview • A short introduction to some letters of interest – R, S, Z • Statistics and computing – applied vs. computational statistics vs. stat. computing – statistical software • The R project • Basic functionality • Empirical application: diabetes in native populations – exploratory analysis – linear regression – tree models • Packages • Summary Some letters R is an interactive computational environment for data analysis, inference and visualization. S is a language for data analysis and graphics, implemented in the commercial software S-PLUS and the open-source software R. Z (aka Achim Zeileis) is a statistician at WU Wien spending a considerable share of his time using and developing R: • for research, • for applied data analysis, • for course administration, • for Web page generation, CD covers, mp3 administration . (but that’s another story). Some letters: R • R is an interactive computational environment for data anal- ysis, inference and visualization. • Developed for the Unix, Windows and Macintosh families of operating systems by an international team. • Released under the GPL (General Public License), similar to the open-source operating system Linux. • Highly extensible through user-defined functions and a fast- growing list of add-on packages. • Based on the S language but with a new underlying imple- mentation. Some letters: S • S is a language for data analysis and graphics developed by John Chambers and co-workers at Bell Labs (of AT&T, now Lucent Technologies). • Exclusively licensed (and eventually sold) to Insightful Corp. as the basis for the commercial statistics system S-PLUS. • Award-winning language which “has forever altered the way how people analyze, visualize and manipulate data. ” (ACM Software System Award 1998 to John Chambers). Some letters: Z Short bio: 1996–2000 University studies in Statistics, Universitat¨ Dortmund, Germany 2000 Dipl.-Stat. (∼ M.Sc.) in Statistics 2000–2003 Research Assistant, SFB “Adaptive Informa- tion Systems and Modelling in Economics and Management Science”, Wirtschaftsuni- versitat¨ Wien, Austria 2003 Dr. rer. nat. (∼ Ph.D.) in Statistics since 2003 Assistant Professor, Department of Statistics & Mathematics, Wirtschaftsuniversitat¨ Wien, Austria Some letters: Z Interests as a student: • Year 1: some interest in exploratory data analysis – tried to learn SAS – failed miserably – decided software is not for me. • Year 2–3: learned a lot about theoretical concepts in statis- tics – did applied work only if necessary – used various com- mercial software packages: SPSS, Minitab, S-PLUS, GLIM, some SAS again, . • Year 4: needed software for seminars and thesis: implement concepts, run simulations, apply to real data – discovered open-source software R – switched from Windows to Linux, from Word to LATEX, from everything else to R – never looked back. Some letters: Z Interests as a researcher: • Statistical computing, • Applied econometrics (in particular: testing, monitoring and dating of structural changes), • Statistical learning (in particular: tree-based models), • Visualization & significance testing. Statistics and computing A large spectrum of statistics involve the use of computers and software programs. Different parts of this spectrum with varying emphasis are the following. Applied statistics: • task: understand structures in data and the underlying mech- anisms. • required: software that provides appropriate statistical tech- niques for application to real data. • tools: preprocessing, inference, visualization, reporting. • extensibility: modify existing tools, customize analysis, define work flows, automatization. Statistics and computing Computational statistics: • task: solve computing-intensive statistical problems. • examples: difficult optimization problems, Markov chain Monte carlo algorithms. • required: efficient implementation/programming language. Statistics and computing Statistical computing: • task: turn theoretical concepts into software • examples: implement a new statistical model so that it can be easily applied to new data sets. • required: flexible software system with programming lan- guage. • tools: object orientation, compiled code, re-usable compo- nents. Of course, these areas are not well separated but overlapping! Software is always the bridge between theoretical concepts and statistical practice. Statistics and computing: Software There is a broad range of statistical software packages, some of the most popular are: Excel most popular spreadsheet, only very basic statistical func- tionality, some programming possible in Visual Basic. SPSS “statistical” spreadsheet, standard statistical tool box (some emphasis on social sciences), programming possible in SPSS language. SAS comprehensive package with numerous interfaces, some emphasis on business solutions, programming in SAS macro language. S-PLUS built on top of S, adds graphical user interface (GUI), spreadsheet, various extensions. R command line interface (CLI), highly extensible, only special- ized GUIs available. Statistics and computing: Excel Statistics and computing: SPSS Statistics and computing: SAS Statistics and computing: SAS Statistics and computing: S-PLUS Statistics and computing: R Statistics and computing: Software GUI CLI learn easy harder flexible not really very repeat tasks tiring easy reproduce results hard easy GUIs are very popular with practitioners, but trained statisticians usually will have to do at least some programming at a certain point. Reproducibility is crucial in scientific work, automatization in many corporate applications. Hence, all large packages offer some “command language” . S/R offers the most complete and modern programming language. The R project History of S: 1976: John Chambers and co-workers at Bell Labs begin work on a project that will become S (S1). 1981: Licenses for a portable Unix version of S outside Bell Labs (S2). 1988: Statistical software package S-PLUS based on S. 1992: Object orientation and statistical modeling toolbox in- cluded (S3). 1993: Exclusively licensed to MathSoft (now Insightful). 1998: New object orientation model introduced (S4). 2004: Sold to Insightful. The R project History of R: 1991: Ross Ihaka and Robert Gentleman begin work on a project that will ultimately become R. 1993: First binary copies of R on Statlib. 1995: R release of sources under the GPL. 1997: R core group is formed. 1998: Comprehensive R Archive Network (CRAN). 1999: DSC meeting in Vienna, first R core meeting. 2000: R 1.0.0 is released. 2001: R Newsletter launched. 2002: R Foundation established. 2004: First useR! conference in Vienna. 2007: R-forge server launched. The R project Home of the R project is http://www.R-project.org/ where manuals, FAQs, links, and many other informations are available. The R software (current version 2.4.0) can be obtained from http://CRAN.R-project.org/ in source and binary form along with many extension packages. The R project Free software: Open-source software like R does not cost money (free as in beer). But it takes time to learn, and as time is money, this talk is mostly about free software in the sense of free as in speach. R is open source, everybody can read the source code, hence you need not to rely on documentation to infer what the software really does. More importantly, everybody can use it, making research reproducible. No owner? R is not in the public domain, you are given a license (GPL) to run the software. The R project The base R system is maintained by the “R Development Core Team” with members from New Zealand, Europe and North America: Douglas Bates, John Chambers, Peter Dalgaard, Robert Gentle- man, Kurt Hornik, Stefano Iacus, Ross Ihaka, Friedrich Leisch, Thomas Lumley, Martin Maechler, Duncan Murdoch, Paul Mur- rell, Martyn Plummer, Brian Ripley, Duncan Temple Lang, Luke Tierney, and Simon Urbanek. But R would not be what it is without the support of a very large and active user community around the world, both in academia and the industry, who contributed by donating code, bug fixes, documentation, packages, discussion on the mailing lists The R project The R user community communicates via means of mailing lists (R-help, R-devel, R-bugs, SIGs) where questions can be asked, problems discussed, bugs reported, solutions suggested. Using the R language interactively allows for a smooth transi- tion from using R to developing in R. Bundles of new functions, manual pages, data sets, examples, demos, documentation can be effectively shared in the R community via means of CRAN packages. Basic functionality • an oversized pocket calculator. • matrix-based language. • full-featured programming language: (statistical) data struc- tures, flow control, object orientation, interfaces to other lan- guages, operating system interaction. • statistical toolbox: exploratory data analysis, inference, (gen- eralized) linear models, multivariate analsyis, time-series analysis, . • production-quality graphics. Basic functionality R> 1 + 1 [1] 2 R> 2^3 [1] 8 R> x <- c(2, 7) R> x [1] 2 7 R> 1/x [1] 0.5000000 0.1428571 Basic functionality R> y <- matrix(c(1, 2, 3, 4), ncol = 2) R> y [,1] [,2] [1,] 1 3 [2,] 2 4 R> y %*% x [,1] [1,] 23 [2,] 32 R> solve(y) [,1] [,2] [1,] -2 1.5 [2,] 1 -0.5 Basic functionality Fundamental language design principle: Everything in R is an object. Every object has a class (e.g., numeric, factor, function, . ) and methods for generic functions are
Load more

Recommended publications
  • R Generation [1] 25
    IN DETAIL > y <- 25 > y R generation [1] 25 14 SIGNIFICANCE August 2018 The story of a statistical programming they shared an interest in what Ihaka calls “playing academic fun language that became a subcultural and games” with statistical computing languages. phenomenon. By Nick Thieme Each had questions about programming languages they wanted to answer. In particular, both Ihaka and Gentleman shared a common knowledge of the language called eyond the age of 5, very few people would profess “Scheme”, and both found the language useful in a variety to have a favourite letter. But if you have ever been of ways. Scheme, however, was unwieldy to type and lacked to a statistics or data science conference, you may desired functionality. Again, convenience brought good have seen more than a few grown adults wearing fortune. Each was familiar with another language, called “S”, Bbadges or stickers with the phrase “I love R!”. and S provided the kind of syntax they wanted. With no blend To these proud badge-wearers, R is much more than the of the two languages commercially available, Gentleman eighteenth letter of the modern English alphabet. The R suggested building something themselves. they love is a programming language that provides a robust Around that time, the University of Auckland needed environment for tabulating, analysing and visualising data, one a programming language to use in its undergraduate statistics powered by a community of millions of users collaborating courses as the school’s current tool had reached the end of its in ways large and small to make statistical computing more useful life.
    [Show full text]
  • Data Analysis in R
    Data Analysis in R Course at a Glance This course will provide an introduction to reproducible data analysis with R (see Syllabus). Instructor Gabriel Baud-Bovy ([email protected] ) Credits: 5 Synopsis This course aims at giving to the student a methodology to analyze experimental results, from how to organize data to the writing of a report. It includes: an introduction to R an introduction to reproducible research with R examples of statistical analysis with R During this course, the student will have to analyze his own data and is expected to read before each course the material that will be made available on this page. The final grade will consist in the evaluation of a report demonstrating familiarity with the concepts and methods presented in the course. As an editor, the instructor will use Notepad++ (together with NppToR) on a Windows Machines but the student might use other ones (e.g., R studio, EMACS+ESS, Lyx, TexWork). The course will use Mardown as typesetting language. For those desirous to work with Latex and/or generate pdf, you will need to install also MikeTex. Syllabus Total of 15 hours Class 1: Case study, Reproducible research Class 2: R fundamental Class 3: Exploratory data analysis and graphical methods in R Class 4: Basic statistics Class 5: To be determined There will be a final examination decided by the instructor. Prerequisites The course assumes some familiarity with programming concepts and data structures (MATLAB, C/C++, Java or any other programming language). Contact the instructor if you have never programmed anything.
    [Show full text]
  • A History of R (In 15 Minutes… and Mostly in Pictures)
    A history of R (in 15 minutes… and mostly in pictures) JULY 23, 2020 Andrew Zief!ler Lunch & Learn Department of Educational Psychology RMCC University of Minnesota LATIS Who am I and Some Caveats Andy Zie!ler • I teach statistics courses in the Department of Educational Psychology • I have been using R since 2005, when I couldn’t put Me (on the EPSY faculty board) SAS on my computer (it didn’t run natively on a Me Mac), and even if I could have gotten it to run, I (everywhere else) couldn’t afford it. Some caveats • Although I was alive during much of the era I will be talking about, I was not working as a statistician at that time (not even as an elementary student for some of it). • My knowledge is second-hand, from other people and sources. Statistical Computing in the 1970s Bell Labs In 1976, scientists from the Statistics Research Group were actively discussing how to design a language for statistical computing that allowed interactive access to routines in their FORTRAN library. John Chambers John Tukey Home to Statistics Research Group Rick Becker Jean Mc Rae Judy Schilling Doug Dunn Introducing…`S` An Interactive Language for Data Analysis and Graphics Chambers sketch of the interface made on May 5, 1976. The GE-635, a 36-bit system that ran at a 0.5MIPS, starting at $2M in 1964 dollars or leasing at $45K/month. ’S’ was introduced to Bell Labs in November, but at the time it did not actually have a name. The Impact of UNIX on ’S' Tom London Ken Thompson and Dennis Ritchie, creators of John Reiser the UNIX operating system at a PDP-11.
    [Show full text]
  • Manual Eviews 6 Espanol Pdf
    Manual Eviews 6 Espanol Pdf Statistical, forecasting, and modeling tools with a simple object-oriented interface. Corel VideoStudio Pro X8 User Guide PDF. 6. Corel VideoStudio Pro User Guide. EViews Illustrated.book Page 1 Thursday, March 19, 2015 9:53 AM Microsoft Corporation. All other product names mentioned in this manual may be Page 6. On this page you can download PDF book Onan Generator Shop Manual Model It can be done by copy-and-paste as well, which is described in EViews' help. This software product, including program code and manual, is copyrighted, and all rights manual or the EViews program. 6. Custom Edit Fields in EViews. 3 Achievements, 4 Performance, 5 Licensing and availability, 6 Software packages editing and embedding SageMath within LaTeX documents, The Python standard library, Archived from the original (PDF) on 2007-06-27. Català · Čeština · Deutsch · Español · Français · Bahasa Indonesia · Italiano · Nederlands. Manual Eviews 6 Espanol Pdf Read/Download Software Lga 775 Related Programs Free Download write Offline Spanish Pilz 4BB0D53E-1167- 4A61-8661-62FB02050D02 EViews 6 Why do I have 2. 0.4 sourceblog.sourceforge.net/maximo- 6-training-manual.pdf 2015-09-03.net/applied-advanced-econometrics-using-eviews.pdf 2015-08- 19 08:25:07 sourceblog.sourceforge.net/manual-de-primavera-p6-en-espanol.pdf. This software product, including program code and manual, is copyrighted, and all you may access the PDF files from within EViews by clicking on Help in the For discussion, see “Command and Capture Window Docking” on page 6. Software Installation for Eviews 8 for SMU Student - Free download as PDF File (.pdf), Text file (.txt) or read online for free.
    [Show full text]
  • August 12-14, Dortmund, Germany
    AASC Austrian Association for Statistical Computing 2008 Program August 12-14, Dortmund, Germany useR! 2008, Dortmund, Germany 1 Contents Greetings and Miscellaneous 2 Maps 5 Social Program 8 Program 9 Tutorials 9 Schedule 10 List of Talks 14 2 useR! 2008, Dortmund, Germany Dear useRs, the following pages provide you with some useful information about useR! 2008, the R user con- ference, taking place at the Fakultät Statistik, Technische Universität Dortmund, Germany from 2008-08-12 to 2008-08-14. Pre-conference tutorials will take place on August 11. The confer- ence is organized by the Fakultät Statistik, Technische Universität Dortmund and the Austrian Association for Statistical Computing (AASC). Apart from challenging and likewise exciting scientific contributions we hope to offer you an attractive conference site and a pleasant social program. With best regards from the organizing team: Uwe Ligges (conference), Achim Zeileis (program), Claus Weihs, Gerd Kopp (local organiza- tion), Friedrich Leisch, and Torsten Hothorn Address / Contact Address: Uwe Ligges Fakultät Statistik Technische Universität Dortmund 44221 Dortmund Germany Phone: +49 231 755 4353 Fax: +49 231 755 4387 e-mail: [email protected] URL: http://www.R-Project.org/useR-2008/ Program Committee Micah Altman, Roger Bivand, Peter Dalgaard, Jan de Leeuw, Ramón Díaz-Uriarte, Spencer Graves, Leonhard Held, Torsten Hothorn, François Husson, Christian Kleiber, Friedrich Leisch, Andy Liaw, Martin Mächler, Kate Mullen, Ei-ji Nakama, Thomas Petzoldt, Martin Theus, and Heather Turner Conference Location Technische Universität Dortmund Campus Nord Mathematikgebäude / Audimax Vogelpothsweg 87 44227 Dortmund Conference Office Opening hours: Monday, August 11: 08:30–19:30 Tuesday, August 12: 08:30–18:30 Wednesday, August 13: 08:30–18:30 Thursday, August 14: 08:30–15:30 useR! 2008, Dortmund, Germany 3 Public Transport The conference site at the university campus and the city hall are best to be reached by public transport.
    [Show full text]
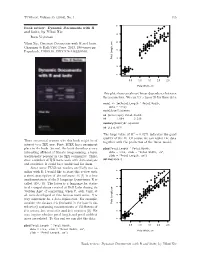
  • Dynamic Documents with R and Knitr, by Yihui Xie 116 Tugboat, Volume 35 (2014), No
    TUGboat, Volume 35 (2014), No. 1 115 ● ● ● Book review: Dynamic Documents with R ● ● ● and knitr, by Yihui Xie ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● Boris Veytsman ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● Yihui Xie, Dynamic Documents with R and knitr. ● ● ● ● ● ● ● ● ● ● ● ● ● ● Chapman & Hall/CRC Press, 2013, 190+xxvi pp. ● ● ● ● ● ● ● ● ● US$ ISBN ● Paperback, 59.95. 978-1482203530. ● ● ● ● Petal Length, cm Petal ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 1 2 3 4 5 6 7 0.5 1.0 1.5 2.0 2.5 Petal Width, cm This plot shows an almost linear dependence between the parameters. We can try a linear fit for these data: model <- lm(Petal.Length ˜ Petal.Width, data = iris) model$coefficients ## (Intercept) Petal.Width ## 1.084 2.230 summary(model)$r.squared ## [1] 0.9271 The large value of R2 = 0.9271 indicates the good quality of the fit. Of course we can replot the data There are several reasons why this book might be of together with the prediction of the linear model: interest to a TEX user. First, LATEX has a prominent place in the book. Second, the book describes a very plot(Petal.Length ˜ Petal.Width, interesting offshoot of literate programming, a topic data = iris, xlab = "Petal Width, cm", traditionally popular in the TEX community. Third, ylab = "Petal Length, cm") abline(model) since a number of TEX users work with data analysis and statistics, R could be a useful tool for them. Since some TUGboat readers are likely not fa- ● ● ● miliar with R, I would like to start this review with ● ● a short description of the software. R [1] is a free ● ● ● ● ● ● ● ● ● ● ● implementation of the S language (sometimes R is ● ● ● ● ● ● ● ● ● ● ● ● ● ● called GNU S).
    [Show full text]
  • An Introduction to R Notes on R: a Programming Environment for Data Analysis and Graphics Version 4.1.1 (2021-08-10)
    An Introduction to R Notes on R: A Programming Environment for Data Analysis and Graphics Version 4.1.1 (2021-08-10) W. N. Venables, D. M. Smith and the R Core Team This manual is for R, version 4.1.1 (2021-08-10). Copyright c 1990 W. N. Venables Copyright c 1992 W. N. Venables & D. M. Smith Copyright c 1997 R. Gentleman & R. Ihaka Copyright c 1997, 1998 M. Maechler Copyright c 1999{2021 R Core Team Permission is granted to make and distribute verbatim copies of this manual provided the copyright notice and this permission notice are preserved on all copies. Permission is granted to copy and distribute modified versions of this manual under the conditions for verbatim copying, provided that the entire resulting derived work is distributed under the terms of a permission notice identical to this one. Permission is granted to copy and distribute translations of this manual into an- other language, under the above conditions for modified versions, except that this permission notice may be stated in a translation approved by the R Core Team. i Table of Contents Preface :::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::: 1 1 Introduction and preliminaries :::::::::::::::::::::::::::::::: 2 1.1 The R environment :::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::: 2 1.2 Related software and documentation ::::::::::::::::::::::::::::::::::::::::::::::: 2 1.3 R and statistics :::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::: 2 1.4 R and the window system ::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
    [Show full text]
  • Modeling Data with Functional Programming in R 2 Preface
    Brian Lee Yung Rowe Modeling Data With Functional Programming In R 2 Preface This book is about programming. Not just any programming, but program- ming for data science and numerical systems. This type of programming usually starts as a mathematical modeling problem that needs to be trans- lated into computer code. With functional programming, the same reasoning used for the mathematical model can be used for the software model. This not only reduces the impedance mismatch between model and code, it also makes code easier to understand, maintain, change, and reuse. Functional program- ming is the conceptual force that binds the these two models together. Most books that cover numerical and/or quantitative methods focus primarily on the mathematics of the model. Once this model is established the computa- tional algorithms are presented without fanfare as imperative, step-by-step, algorithms. These detailed steps are designed for machines. It is often difficult to reason about the algorithm in a way that can meaningfully leverage the properties of the mathematical model. This is a shame because mathematical models are often quite beautiful and elegant yet are transformed into ugly and cumbersome software. This unfortunate outcome is exacerbated by the real world, which is messy: data does not always behave as desired; data sources change; computational power is not always as great as we wish; re- porting and validation workflows complicate model implementations. Most theoretical books ignore the practical aspects of working in thefield. The need for a theoretical and structured bridge from the quantitative methods to programming has grown as data science and the computational sciences become more pervasive.
    [Show full text]
  • The R Journal Volume 3/2, December 2011
    The Journal Volume 3/2, December 2011 A peer-reviewed, open-access publication of the R Foundation for Statistical Computing Contents Editorial..................................................3 Contributed Research Articles Creating and Deploying an Application with (R)Excel and R...................5 glm2: Fitting Generalized Linear Models with Convergence Problems.............. 12 Implementing the Compendium Concept with Sweave and DOCSTRIP............. 16 Watch Your Spelling!........................................... 22 Ckmeans.1d.dp: Optimal k-means Clustering in One Dimension by Dynamic Programming 29 Nonparametric Goodness-of-Fit Tests for Discrete Null Distributions............... 34 Using the Google Visualisation API with R.............................. 40 GrapheR: a Multiplatform GUI for Drawing Customizable Graphs in R............. 45 rainbow: An R Package for Visualizing Functional Time Series.................. 54 Programmer’s Niche Portable C++ for R Packages...................................... 60 News and Notes R’s Participation in the Google Summer of Code 2011....................... 64 Conference Report: useR! 2011..................................... 68 Forthcoming Events: useR! 2012.................................... 70 Changes in R............................................... 72 Changes on CRAN............................................ 84 News from the Bioconductor Project.................................. 86 R Foundation News........................................... 87 2 The Journal is a peer-reviewed publication
    [Show full text]
  • The R Journal, June 2012
    The Journal Volume 2/1, June 2010 A peer-reviewed, open-access publication of the R Foundation for Statistical Computing Contents Editorial..................................................3 Contributed Research Articles IsoGene: An R Package for Analyzing Dose-response Studies in Microarray Experiments..5 MCMC for Generalized Linear Mixed Models with glmmBUGS ................. 13 Mapping and Measuring Country Shapes............................... 18 tmvtnorm: A Package for the Truncated Multivariate Normal Distribution........... 25 neuralnet: Training of Neural Networks............................... 30 glmperm: A Permutation of Regressor Residuals Test for Inference in Generalized Linear Models.................................................. 39 Online Reproducible Research: An Application to Multivariate Analysis of Bacterial DNA Fingerprint Data............................................ 44 Two-sided Exact Tests and Matching Confidence Intervals for Discrete Data.......... 53 Book Reviews A Beginner’s Guide to R......................................... 59 News and Notes Conference Review: The 2nd Chinese R Conference........................ 60 Introducing NppToR: R Interaction for Notepad++......................... 62 Changes in R 2.10.1–2.11.1........................................ 64 Changes on CRAN............................................ 72 News from the Bioconductor Project.................................. 85 R Foundation News........................................... 86 2 The Journal is a peer-reviewed publication of
    [Show full text]
  • From Datasets to Resultssets in Stata
    From datasets to resultssets in Stata Roger Newson King's College London, London, UK [email protected] http://www.kcl-phs.org.uk/rogernewson/ Distributed at the 10th UK Stata Users' Group Meeting on 29 June 2004 1 What are resultssets? A resultsset is a Stata dataset created as output by a Stata command. It may be simply listed to the Stata log and/or output to a disk ¯le and/or written to the memory, overwriting any pre-existing dataset. If you are a SAS user converting to Stata, then note that Stata datasets do the job of SAS data sets, and Stata resultssets do the job of SAS output data sets. 1.1 Why resultssets? In general, a Stata dataset, or a dataset in any other format, should contain one observation per thing, and data on attributes of things. For instance, in the medical sector, a dataset might have one observation per patient, and data on the patient's baseline characteristics. Alternatively, a dataset might have one observation per visit to a health centre, and data on the state of the patient who made the visit. Usually, the variables in a dataset are either primary key variables, which identify the things corresponding to the observations, or non-key variables, which identify interesting attributes of those things. For instance, if there is one observation per patient, then one of the variables is usually a patient ID number, which identi¯es the observation uniquely. Or, if there is one observation per visit, and a patient may only make one visit per day, then the primary key variables are usually patient ID and visit date.
    [Show full text]
  • Symbolic Formulae for Linear Mixed Models Arxiv:1911.08628V1 [Stat
    Symbolic Formulae for Linear Mixed Models∗ Emi Tanaka1,2,* Francis K. C. Hui3 1 School of Mathematics and Statistics, The University of Sydney, NSW, Australia, 2006 2 Department of Econometrics and Business Statistics, Monash University, VIC, Australia, 3800 3 Research School of Finance, Actuarial Studies & Statistics, Australian National University, ACT, Australia, 2601 < [email protected] Abstract A statistical model is a mathematical representation of an often simpli- fied or idealised data-generating process. In this paper, we focus on a par- ticular type of statistical model, called linear mixed models (LMMs), that is widely used in many disciplines e.g. agriculture, ecology, econometrics, psychology. Mixed models, also commonly known as multi-level, nested, hierarchical or panel data models, incorporate a combination of fixed and random effects, with LMMs being a special case. The inclusion of random effects in particular gives LMMs considerable flexibility in accounting for many types of complex correlated structures often found in data. This flex- arXiv:1911.08628v1 [stat.ME] 19 Nov 2019 ibility, however, has given rise to a number of ways by which an end-user can specify the precise form of the LMM that they wish to fit in statistical software. In this paper, we review the software design for specification of the LMM (and its special case, the linear model), focusing in particular on the use of high-level symbolic model formulae and two popular but contrasting R-packages in lme4 and asreml. ∗Supported by R Consortium 1 1 Introduction Statistical models are mathematical formulation of often simplified real world phe- nomena, the use of which is ubiquitous in many data analyses.
    [Show full text]