DOCSLIB.ORG

194 Publications of the Measurements of The

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
194 Publications of the Measurements of The 194 PUBLICATIONS OF THE MEASUREMENTS OF THE RADIATION FROM THE PLANET MERCURY By Edison Pettit and Seth Β. Nicholson The total radiation from Mercury and its transmission through a water cell and through a microscope cover glass were measured with the thermocouple at the 60-inch reflector on June 17, 1923, and again at the 100-inch reflector on June 21st. Since the thermocouple is compensated for general diffuse radiation it is possible to measure the radiation from stars and planets in full daylight quite as well as at night (aside from the effect of seeing), and in the present instance Mercury and the comparison stars were observed near the meridian between th hours of 9 a. m. and 1 p. m. The thermocouple cell is provided with a rock salt window 2 mm thick obtained from the Smithsonian Institution through the kindness of Dr. Abbot. The transmission curves for the water cell and microscope cover glass have been carefully de- termined : those for the former may be found in Astrophysical Journal, 56, 344, 1922; those for the latter, together with the curves for rock salt, fluorite and the atmosphere for average observing conditions are given in Figure 1. We may consider the water cell to transmit in the region of 0.3/a to 1.3/x and the covér glass to transmit between 0.3μ and 5.5/1,, although some radiation is transmitted by the cover glass up to 7.5/a. The atmosphere acts as a screen transmitting prin- cipally in two regions 0.3μ, to 2,5μ and 8μ to 14μ, respectively. It is chiefly through this latter band that planetary radiation (which may be defined as radiation emitted by the planet due to the warming of its surface) reaches us, although a small amount is also transmitted by the weak band 4.5μ to 6μ. The diameter of the image of the planet when observed with the 100-inch telescope on June 21, was 0.55 mm, while the dia- meter of the receivers is 0.40 mm. The phase angle being 70°, the image covered 50 per cent of the area of the receiver with about 18 per cent of the image overlapping at the horns. As the deflections were too great, the registering apparatus1 was © Astronomical Society of the Pacific · Provided by the NASA Astrophysics Data System ASTRONOMICAL SOCIETY OF THE PACIFIC 195 used at 1/5 scale distance. Under these conditions Mercury gave a deflection of 132.2 mm on direct exposure, but only 33.1 mm when a microscope cover glass was interposed in the beam, and 9.0 mm when the water cell was used. Cap ella gave a de- flection of 23.0 mm on direct exposure. The transmission of radiation from Mercury through water cell and cover glass as a percentage of the total radiation observed, together with similar data for the Moon, Jupiter, Saturn, the Sun and two stars is given in Table I. The data for the Moon were obtained by taking drift curves across the disk on March 24 when the phase angle was about 85°, some- what greater than that of Mercury on June 21. The curves Transmission—per cent Wave-length—μ Fig. 1. Transmission curves to. the atmosphere above Mt. Wilson (the unlabelled curve having eight minima between 0 and 8^, and two maxima · between 8 and 14m), microscope cover glass, fluorite, and rock salt. which were taken along the line connecting the middle of the limb with a point near the middle of the terminator, have nearly the form of a right angle triangle, showing that the radiation for a point along the line observed is proportional to its distance from the terminator, being zero at the termina- tor and rising to a maximum at the limb. Drift curves taken through the water cell show that the percentage of transmis- sion through this cell is practically uniform from the limb to a point at about 70 per cent of the distance to the terminator. © Astronomical Society of the Pacific · Provided by the NASA Astrophysics Data System 196 PUBLICATIONS OF THE Here the water cell deflection becomes so small that further observations must be made before definitive transmissions can be obtained. No cover glass ratio was obtained for the Moon, but the value given here is inferred from observations on the ' Moon made with a thermocouple provided with a cover glass window, which gave 33.3 per cent transmission for the water cell. TABLE I Transmission of Radiation Object Water Cell Cover Glass Rock Salt Mercury 6.9 24.5 100 Moon 8.0 24.0 ' Jupiter 72.4 86.6 Jupiter dark band 70.3 " Saturn 70.5 " Saturn Ring 69.7 " Sun 67.5 92.2 Capella 60.0 93.2 Vega 77.6 93.1 It will be noted that the transmissions of the cover glass for the Sun, Capella, and Vega are nearly the same, deviating' little from the mean 92.8 per cent. We may infer from this that the lack of perfect transmission is due to radiation re- flected from the cover glass when it is interposed in the beam, since practically no radiation is emitted by these bodies outside the region of high cover-glass transmission. Indeed this proves to be the case since a measurement of the reflected radiation from a cover glass when a beam of sunlight falls upon it at normal incidence gives 7.3 per cent. Applying this as a cor- rection to the second and third columns and taking the differ- ences we obtain Table II, which represents the radiation found in the regions 0.3μ to 1.3/a, 1.3/i. to 5.5^ and 8/x to 14/x, re- spectively. TABLE II Transmission Corrected for Reflection from Screens 0.3^ to 1.3/a 1.3/a to 5.5/¿ 8αι to 14/ι Mercury 7.4 19.0 73.6 Moon 8.6 17.3 74.1 Jupiter 78.1 15.3 6.6 Jupiter dark band 75.8 Saturn 76.0 Saturn Ring 75.1 Sun 72.8 27.2 0 Capella 64.8 35.2 0 Vega 83.7 16.3 0 1Astrophysical Journal, 56, 343, 1922. © Astronomical Society of the Pacific · Provided by the NASA Astrophysics Data System ASTRONOMICAL SOCIETY OF THE PACIFIC 197 The transmission in the fourth column then, may be taken to represent the planetary radiation entering our atmosphere through the transmission band 8μ to 14μ. Several facts are at once apparent: (1) Mercury, like the Moon, emits a large amount of planetary radiation, which may indicate that, like the Moon, it has little or no atmosphere; (2) The spectral distribu- tion of the radiation from Mercury is almost precisely that of the Moon, hence we may conclude that the two bodies have nearly the same surface temperature; (3) The radiation from Saturn's rings is practically all reflected sunlight. This might be expected from a consideration of the small value of the solar constant at Saturn's distance and the nature of the rings; (4) There is some planetary radiation from Jupiter. Conclusion (1) is also to be expected in view of the evidence from visual observations of the planet's surface, and its appear- ance during transit over the Sun's disk. One hesitates to ac- cept conclusion (2), that the temperatures of Mercury and the Moon are the same, however, in view of the relative nearness of the planet to the Sun. We may approach the problem from another angle by com- paring directly the intensity of the planetary radiation from the Moon and Mercury. If the Moon were at such a distance that its image were of the same diameter as the receiver, it would give a deflection equal to the average deflection obtained over its surface, when due allowance is made for the fact that the total area of the receiver does not receive radiation except at full phase. This quantity would be independent of the Moon's distance as long as this condition prevails. We may obtain the average deflection over the Moon's surface in still another way. The insolation, and hence the planetary radiation is isometric along small circles on the Moon's surface whose planes are parallel to the terminator, if we may neglect the possible effects of rotation. This is also true of the reflected light. Now, since the rate of radiation from a point on the Moon's surface along a line joining the middle of the limb and the middle of the terminator is proportional to its distance from the terminator for a phase angle of 85°, as was found from the drift curves of March 24, this must also be true for any line parallel to it. By © Astronomical Society of the Pacific · Provided by the NASA Astrophysics Data System 198 PUBLICATIONS OF THE integration or mechanical quadratures it is easy to show that the average deflection which would be obtained by exposing a small receiver to an image of the Moon near first quarter i$ , equal to the value at the middle of the limb multiplied by the factor 0.43. This also is independent of the Moon's distance. Let us apply the first method of determining the average radia- tion independently of the distance to Mercury and the second method to the Moon and compare the results. The observed deflection from Mercury was 132 mm and since only 50 per cent of the receiver was covered by the image this deflection must be multiplied by the factor 2 in order to make it comparable with that for the Moon.
Load more

Recommended publications
  • Phases of Venus and Galileo
    Galileo and the phases of Venus I) Periods of Venus 1) Synodical period and phases The synodic period1 of Venus is 584 days The superior2 conjunction occured on 11 may 1610. Calculate the date of the quadrature, of the inferior conjunction and of the next superior conjunction, supposing the motions of the Earth and Venus are circular and uniform. In fact the next superior conjunction occured on 11 december 1611 and inferior conjunction on 26 february 1611. 2) Sidereal period The sidereal period of the Earth is 365.25 days. Calculate the sidereal period of Venus. II) Phases on Venus in geo and heliocentric models 1) Phases in differents models 1) Determine the phases of Venus in geocentric models, where the Earth is at the center of the universe and planets orbit around (Venus “above” or “below” the sun) * Pseudo-Aristoteles model : Earth (center)-Moon-Sun-Mercury-Venus-Mars-Jupiter-Saturne * Ptolemeo’s model : Earth (center)-Moon-Mercury-Venus-Sun-Mars-Jupiter-Saturne 2) Determine the phases of Venus in the heliocentric model, where planets orbit around the sun. Copernican system : Sun (center)-Mercury-Venus-Earth-Mars-Jupiter-Saturne 2) Observations of Galileo Galileo (1564-1642) observed Venus in 1610-1611 with a telescope. Read the letters of Galileo. May we conclude that the Copernican model is the only one available ? When did Galileo begins to observe Venus? Give the approximate dates of the quadrature and of the inferior conjunction? What are the approximate dates of the 5 observations of Galileo supposing the figure from the Essayer, was drawn in 1610-1611 1 The synodic period is the time that it takes for the object to reappear at the same point in the sky, relative to the Sun, as observed from Earth; i.e.
    [Show full text]
  • Absolute Magnitude and Slope Parameter G Calibration of Asteroid 25143 Itokawa
    Meteoritics & Planetary Science 44, Nr 12, 1849–1852 (2009) Abstract available online at http://meteoritics.org Absolute magnitude and slope parameter G calibration of asteroid 25143 Itokawa Fabrizio BERNARDI1, 2*, Marco MICHELI1, and David J. THOLEN1 1Institute for Astronomy, University of Hawai‘i, 2680 Woodlawn Drive, Honolulu, Hawai‘i 96822, USA 2Dipartimento di Matematica, Università di Pisa, Largo Pontecorvo 5, 56127 Pisa, Italy *Corresponding author. E-mail: [email protected] (Received 12 December 2008; revision accepted 27 May 2009) Abstract–We present results from an observing campaign of 25143 Itokawa performed with the 2.2 m telescope of the University of Hawai‘i between November 2000 and September 2001. The main goal of this paper is to determine the absolute magnitude H and the slope parameter G of the phase function with high accuracy for use in determining the geometric albedo of Itokawa. We found a value of H = 19.40 and a value of G = 0.21. INTRODUCTION empirical relation between a polarization curve and the albedo. Our work will take advantage by the post-encounter The present work was performed as part of our size determination obtained by Hayabusa, allowing a more collaboration with NASA to support the space mission direct conversion of the ground-based photometric Hayabusa (MUSES-C), which in September 2005 had a information into a physically meaningful value for the albedo. rendezvous with the near-Earth asteroid 25143 Itokawa. We Another important goal of these observations was to used the 2.2 m telescope of the University of Hawai‘i at collect more data for a possible future detection of the Mauna Kea.
    [Show full text]
  • The H and G Magnitude System for Asteroids
    Meetings The BAA Observers’ Workshops The H and G magnitude system for asteroids This article is based on a presentation given at the Observers’ Workshop held at the Open University in Milton Keynes on 2007 February 24. It can be viewed on the Asteroids & Remote Planets Section website at http://homepage.ntlworld.com/ roger.dymock/index.htm When you look at an asteroid through the eyepiece of a telescope or on a CCD image it is a rather unexciting point of light. However by analysing a number of images, information on the nature of the object can be gleaned. Frequent (say every minute or few min- Figure 2. The inclined orbit of (23) Thalia at opposition. utes) measurements of magnitude over periods of several hours can be used to generate a lightcurve. Analysis of such a lightcurve Absolute magnitude, H: the V-band magnitude of an asteroid if yields the period, shape and pole orientation of the object. it were 1 AU from the Earth and 1 AU from the Sun and fully Measurements of position (astrometry) can be used to calculate illuminated, i.e. at zero phase angle (actually a geometrically the orbit of the asteroid and thus its distance from the Earth and the impossible situation). H can be calculated from the equation Sun at the time of the observations. These distances must be known H = H(α) + 2.5log[(1−G)φ (α) + G φ (α)], where: in order for the absolute magnitude, H and the slope parameter, G 1 2 φ (α) = exp{−A (tan½ α)Bi} to be calculated (it is common for G to be given a nominal value of i i i = 1 or 2, A = 3.33, A = 1.87, B = 0.63 and B = 1.22 0.015).
    [Show full text]
  • Phase Integral of Asteroids Vasilij G
    A&A 626, A87 (2019) Astronomy https://doi.org/10.1051/0004-6361/201935588 & © ESO 2019 Astrophysics Phase integral of asteroids Vasilij G. Shevchenko1,2, Irina N. Belskaya2, Olga I. Mikhalchenko1,2, Karri Muinonen3,4, Antti Penttilä3, Maria Gritsevich3,5, Yuriy G. Shkuratov2, Ivan G. Slyusarev1,2, and Gorden Videen6 1 Department of Astronomy and Space Informatics, V.N. Karazin Kharkiv National University, 4 Svobody Sq., Kharkiv 61022, Ukraine e-mail: [email protected] 2 Institute of Astronomy, V.N. Karazin Kharkiv National University, 4 Svobody Sq., Kharkiv 61022, Ukraine 3 Department of Physics, University of Helsinki, Gustaf Hällströmin katu 2, 00560 Helsinki, Finland 4 Finnish Geospatial Research Institute FGI, Geodeetinrinne 2, 02430 Masala, Finland 5 Institute of Physics and Technology, Ural Federal University, Mira str. 19, 620002 Ekaterinburg, Russia 6 Space Science Institute, 4750 Walnut St. Suite 205, Boulder CO 80301, USA Received 31 March 2019 / Accepted 20 May 2019 ABSTRACT The values of the phase integral q were determined for asteroids using a numerical integration of the brightness phase functions over a wide phase-angle range and the relations between q and the G parameter of the HG function and q and the G1, G2 parameters of the HG1G2 function. The phase-integral values for asteroids of different geometric albedo range from 0.34 to 0.54 with an average value of 0.44. These values can be used for the determination of the Bond albedo of asteroids. Estimates for the phase-integral values using the G1 and G2 parameters are in very good agreement with the available observational data.
    [Show full text]
  • Phase Angle, Degrees R Educed V M a Gn Itu
    Lunar and Planetary Science XXX 1595.pdf MAGNITUDE PHASE DEPENDENCE OF ASTEROID 433 EROS. Yu. N. Krugly and V. G. Shevchenko, Astronomical Observatory of Kharkiv State University, 35 Sumska str., 310022 Kharkiv, Ukraine, e-mail address: [email protected]. Introduction: 10.2 The NEAR spacecraft is coming to the near-Earth asteroid 433 Eros and it will provide us an important information about this body. The data obtained from 10.7 the space experiments will require disk-integral obser- vations of the asteroids at various aspects and solar phase angles. In that connection the ground-based ob- servations of 433 Eros can be very useful. We present 11.2 the results of long-term observations of 433 Eros in- cluding measurements of the magnitude phase depend- ence. V Magnitude Reduced 11.7 Observations: 0 10203040 433 Eros was observed photometrically during three Phase Angle, degrees apparitions in 1993, 1995 and 1997 using the 70-cm reflector at Kharkiv Observatory and 1-m reflector at Figure 1. Phase curve of Eros obtained from the Simeis Observatory (Ukraine). The observations were observations during the 1993 opposition. Solid line is carried out in standard V band. Table gives aspect data an approximation by function proposed in [3]. Dashed (ecliptic coordinates and phase angle) of the asteroid at line is a best fit approximation of a linear part of the the midtimes of the observations. The last column pre- phase curve. sents magnitudes of the asteroid reduced to the primary maximum of the lightcurve. Parameters of HG-function [1] were determinated Date λ2000 β2000 P.A.
    [Show full text]
  • Asteroid Photometric and Polarimetric Phase Curves: Joint Linear-Exponential Modeling
    Meteoritics & Planetary Science 44, Nr 12, 1937–1946 (2009) Abstract available online at http://meteoritics.org Asteroid photometric and polarimetric phase curves: Joint linear-exponential modeling K. MUINONEN1, 2, A. PENTTILÄ1, A. CELLINO3, I. N. BELSKAYA4, M. DELBÒ5, A. C. LEVASSEUR-REGOURD6, and E. F. TEDESCO7 1University of Helsinki, Observatory, Kopernikuksentie 1, P.O. BOX 14, FI-00014 U. Helsinki, Finland 2Finnish Geodetic Institute, Geodeetinrinne 2, P.O. Box 15, FI-02431 Masala, Finland 3INAF-Osservatorio Astronomico di Torino, strada Osservatorio 20, 10025 Pino Torinese, Italy 4Astronomical Institute of Kharkiv National University, 35 Sumska Street, 61035 Kharkiv, Ukraine 5IUMR 6202 Laboratoire Cassiopée, Observatoire de la Côte d’Azur, BP 4229, 06304 Nice, Cedex 4, France 6UPMC Univ. Paris 06, UMR 7620, BP3, 91371 Verrières, France 7Planetary Science Institute, 1700 E. Ft. Lowell Road, Tucson, Arizona 85719, USA *Corresponding author. E-mail: [email protected] (Received 01 April, 2009; revision accepted 18 August 2009) Abstract–We present Markov-Chain Monte-Carlo methods (MCMC) for the derivation of empirical model parameters for photometric and polarimetric phase curves of asteroids. Here we model the two phase curves jointly at phase angles գ25° using a linear-exponential model, accounting for the opposition effect in disk-integrated brightness and the negative branch in the degree of linear polarization. We apply the MCMC methods to V-band phase curves of asteroids 419 Aurelia (taxonomic class F), 24 Themis (C), 1 Ceres (G), 20 Massalia (S), 55 Pandora (M), and 64 Angelina (E). We show that the photometric and polarimetric phase curves can be described using a common nonlinear parameter for the angular widths of the opposition effect and negative-polarization branch, thus supporting the hypothesis of common physical mechanisms being responsible for the phenomena.
    [Show full text]
  • After Neptune Odyssey Design
    Concept Study Team We are enormously proud to be part of a large national and international team many of whom have contributed their time in order to make this study a very enjoyable and productive experience. Advancing science despite the lockdown. Team Member Role Home Institution Team Member Role Home Institution Abigail Rymer Principal Investigator APL George Hospodarsky Plasma Wave Expert U. of Iowa Kirby Runyon Project Scientist APL H. Todd Smith Magnetospheric Science APL Brenda Clyde Lead Engineer APL Hannah Wakeford Exoplanets U. of Bristol, UK Susan Ensor Project Manager APL Imke de Pater Neptune expert Berkeley Clint Apland Spacecraft Engineer APL Jack Hunt GNC Engineer APL Jonathan Bruzzi Probe Engineer APL Jacob Wilkes RF Engineer APL Janet Vertisi Sociologist, teaming expert Princeton James Roberts Geophysicist APL Kenneth Hansen NASA HQ Representative NASA HQ Jay Feldman Probe Engineer NASA Ames Krista Soderlund Neptune WG Co-lead U. of Texas Jeremy Rehm Outreach APL Kunio Sayanagi Neptune WG Co-lead Hampton U. Jorge Nunez Payload Manager APL Alan Stern Triton WG Co-lead SwRI Joseph Williams Probe Engineer NASA Ames Lynne Quick Triton WG Co-lead GSFC Juan Arrieta Tour Design NablaZero lab Tracy Becker Icies and Rings WG Co-lead SwRI Kathleen Mandt Triton Science APL Matthew Hedman Icies and Rings WG Co-lead U. of Idaho Kelvin Murray Schedule APL Ian Cohen Aurora/Mag WG Co-lead APL Kevin Stevenson Exoplanets APL Frank Crary Aurora/Mag WG Co-lead U. of Colorado Kurt Gantz Mechanical Design Engineer APL Jonathan Fortney Exoplanets WG Lead UCSC Larry Wolfarth Cost Analysis APL Adam Masters Magnetospheric Science Imperial College Leigh Fletcher Physicist U.
    [Show full text]
  • Photometric Correction of Chang'e-1 Interference Imaging
    remote sensing Technical Note Photometric Correction of Chang’E-1 Interference Imaging Spectrometer’s (IIM) Limited Observing Geometries Data with Hapke Model Xuesen Xu 1,2,3 , Jianjun Liu 2,*, Dawei Liu 2, Bin Liu 2 and Rong Shu 1,3 1 School of Physics and Optoelectronic Engineering, Hangzhou Institute for Advanced Study, University of Chinese Academy of Sciences, Hangzhou 310024, China; [email protected] (X.X.); [email protected] (R.S.) 2 Key Laboratory of Lunar and Deep Space Exploration, National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100101, China; [email protected] (D.L.); [email protected] (B.L.) 3 Key Laboratory of Space Active Opto-Electronics Technology, Chinese Academy of Sciences, Shanghai 200083, China * Correspondence: [email protected] Received: 2 September 2020; Accepted: 4 November 2020; Published: 10 November 2020 Abstract: The main objective of this study is to develop a Hapke photometric model that is suited for Chang’E-1 (CE-1) Interference Imaging Spectrometer (IIM) data. We first divided the moon into three areas including ‘maria’, ‘new highland’ and old ‘highland’ with similar photometry characteristic based on the Hapke parameters of the moon derived from Lunar Reconnaissance Orbiter Camera (LROC) Wide Angle Camera (WAC) multispectral data. Then, we selected the sample data in the ‘maria’ area and obtained a new set of Hapke model’s parameters that can best fit these data. Result shows that photometric correction using Hapke model with these new derived parameters can eliminate the effect of variations in viewing and luminating geometry, especially ‘opposition surge’, more efficiently than the empirical model.
    [Show full text]
  • Direct Imaging of Exoplanets
    Direct Imaging of Exoplanets Wesley A. Traub Jet Propulsion Laboratory, California Institute of Technology Ben R. Oppenheimer American Museum of Natural History A direct image of an exoplanet system is a snapshot of the planets and disk around a central star. We can estimate the orbit of a planet from a time series of images, and we can estimate the size, temperature, clouds, atmospheric gases, surface properties, rotation rate, and likelihood of life on a planet from its photometry, colors, and spectra in the visible and infrared. The exoplanets around stars in the solar neighborhood are expected to be bright enough for us to characterize them with direct imaging; however, they are much fainter than their parent star, and separated by very small angles, so conventional imaging techniques are totally inadequate, and new methods are needed. A direct-imaging instrument for exoplanets must (1) suppress the bright star’s image and diffraction pattern, and (2) suppress the star’s scattered light from imperfections in the telescope. This chapter shows how exoplanets can be imaged by controlling diffraction with a coronagraph or interferometer, and controlling scattered light with deformable mirrors. 1. INTRODUCTION fainter than its star, and separated by 12.7 arcsec (98 AU at 7.7 pc distance). It was detected at two epochs, clearly showing The first direct images of exoplanets were published in common motion as well as orbital motion (see inset). 2008, fully 12 years after exoplanets were discovered, and Figure 2 shows a near-infrared composite image of exo- after more than 300 of them had been measured indirectly planets HR 8799 b,c,d by Marois et al.
    [Show full text]
  • Absolute Magnitudes and Phase Coefficients of Trans-Neptunian Objects
    A&A 586, A155 (2016) Astronomy DOI: 10.1051/0004-6361/201527161 & c ESO 2016 Astrophysics Absolute magnitudes and phase coefficients of trans-Neptunian objects A. Alvarez-Candal1, N. Pinilla-Alonso2, J. L. Ortiz3,R.Duffard3, N. Morales3, P. Santos-Sanz3, A. Thirouin4, and J. S. Silva1 1 Observatório Nacional / MCTI, Rua General José Cristino 77, 20921-400 Rio de Janeiro, RJ, Brazil e-mail: [email protected] 2 Department of Earth and Planetary Sciences, University of Tennessee, Knoxville, TN, 37996, USA 3 Instituto de Astrofísica de Andalucía, CSIC, Apt 3004, 18080 Granada, Spain 4 Lowell Observatory, 1400 W Mars Hill Rd, Flagstaff, 86001 Arizona, USA Received 10 August 2015 / Accepted 27 November 2015 ABSTRACT Context. Accurate measurements of diameters of trans-Neptunian objects (TNOs) are extremely difficult to obtain. Thermal modeling can provide good results, but accurate absolute magnitudes are needed to constrain the thermal models and derive diameters and geometric albedos. The absolute magnitude, HV , is defined as the magnitude of the object reduced to unit helio- and geocentric distances and a zero solar phase angle and is determined using phase curves. Phase coefficients can also be obtained from phase curves. These are related to surface properties, but only few are known. Aims. Our objective is to measure accurate V-band absolute magnitudes and phase coefficients for a sample of TNOs, many of which have been observed and modeled within the program “TNOs are cool”, which is one of the Herschel Space Observatory key projects. Methods. We observed 56 objects using the V and R filters. These data, along with those available in the literature, were used to obtain phase curves and measure V-band absolute magnitudes and phase coefficients by assuming a linear trend of the phase curves and considering a magnitude variability that is due to the rotational light-curve.
    [Show full text]
  • The Magnitudes of the Planets
    Submitted to Sky&Telescope magazine where it was edited and published in the January 2011 issue: The Magnitudes of the Planets Anthony Mallama 2010 September 30 “How bright is that planet?” Thousands of amateur sky watchers ask this question every year and many look to S&T’s Celestial Calendar for the answer. This article tells how the magnitudes of our solar system neighbors are predicted and explains what we can learn about planets based on their luminosities. The distance from the planet to the observer and that from the planet to the Sun both affect its brightness. The ‘inverse square law’ of distance means that a planet twice as far away appears one- fourth as bright. The phase angle corresponding to the planet’s crescent, quarter, gibbous or full shape also contributes to its magnitude. A disk seen fully illuminated by the Sun is at phase angle 0 degrees while the thinnest crescent approaches phase angle 180. Distance and phase are geometrical effects. Two physical factors that influence brightness are the planet’s size and its reflectivity. Luminosity depends directly on the surface area of the body. Twice the area produces twice the brightness. Reflectivity indicates how a planetary ground or cloud layer redirects the sunlight that it receives. This is the most enlightening aspect of planetary photometry (the study of luminosities) because characteristics of the planets themselves are revealed. Clouds reflect a large fraction of the incoming light and they distribute it over a wide angle. Meanwhile solid surfaces reflect less light and return it more strongly in the direction from which it came.
    [Show full text]
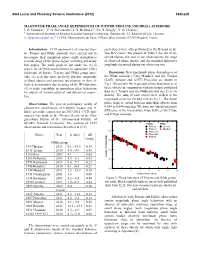
  • MAGNITUDE PHASE ANGLE DEPENDENCES of JUPITER TROJANS and HILDA ASTEROIDS IG Slyusarev1, VG Shevchenko1, in Belskaya1,2
    43rd Lunar and Planetary Science Conference (2012) 1885.pdf MAGNITUDE PHASE ANGLE DEPENDENCES OF JUPITER TROJANS AND HILDA ASTEROIDS I. G. Slyusarev1, V. G. Shevchenko1, I. N. Belskaya1,2, Yu. N. Krugly1, V. G. Chiorny1, 1 Astronomical Institute of Kharkiv Karazin National University, Sumska Str. 35, Kharkiv 61022, Ukraine ([email protected]), 2 LESIA, Observatoire de Paris, 5 Place Jules Janssen, 92195 Meudon, France Introduction: CCD photometry of selected Jupi- each object were also performed in the B band to de- ter Trojans and Hilda asteroids were carried out to fine B-V colors. We present in Table 1 the list of ob- investigate their magnitude phase angle dependences served objects, the year of our observations, the range in wide range of the phase angles, including extremely of observed phase angles, and the maximal lightcurve low angles. The main goals of our study are (1) to amplitude measured during our observing run. search for differences/similarities in opposition effect behaviour of Jupiter Trojans and Hilda group aster- Discussion: New magnitude phase dependences of oids; (2) to define more precisely absolute magnitude the Hilda asteroid (1748) Mauderli and the Trojans of these objects and estimate uncertanties in their al- (2207) Antenor and (2357) Phereclos are shown in bedo determinations due to using of the HG-function; Fig.1. We present the magnitude phase dependences of (3) to study variability in opposition effect behaviour these objects in comparison with previously published for objects of various physical and dynamical proper- data for 3 Trojans and one Hilda asteroid (see [2,3] for ties.
    [Show full text]