IIR Filter Design Example
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Emotion Perception and Recognition: an Exploration of Cultural Differences and Similarities
Emotion Perception and Recognition: An Exploration of Cultural Differences and Similarities Vladimir Kurbalija Department of Mathematics and Informatics, Faculty of Sciences, University of Novi Sad Trg Dositeja Obradovića 4, 21000 Novi Sad, Serbia +381 21 4852877, [email protected] Mirjana Ivanović Department of Mathematics and Informatics, Faculty of Sciences, University of Novi Sad Trg Dositeja Obradovića 4, 21000 Novi Sad, Serbia +381 21 4852877, [email protected] Miloš Radovanović Department of Mathematics and Informatics, Faculty of Sciences, University of Novi Sad Trg Dositeja Obradovića 4, 21000 Novi Sad, Serbia +381 21 4852877, [email protected] Zoltan Geler Department of Media Studies, Faculty of Philosophy, University of Novi Sad dr Zorana Đinđića 2, 21000 Novi Sad, Serbia +381 21 4853918, [email protected] Weihui Dai School of Management, Fudan University Shanghai 200433, China [email protected] Weidong Zhao School of Software, Fudan University Shanghai 200433, China [email protected] Corresponding author: Vladimir Kurbalija, tel. +381 64 1810104 ABSTRACT The electroencephalogram (EEG) is a powerful method for investigation of different cognitive processes. Recently, EEG analysis became very popular and important, with classification of these signals standing out as one of the mostly used methodologies. Emotion recognition is one of the most challenging tasks in EEG analysis since not much is known about the representation of different emotions in EEG signals. In addition, inducing of desired emotion is by itself difficult, since various individuals react differently to external stimuli (audio, video, etc.). In this article, we explore the task of emotion recognition from EEG signals using distance-based time-series classification techniques, involving different individuals exposed to audio stimuli. -

Frequency Response
EE105 – Fall 2015 Microelectronic Devices and Circuits Frequency Response Prof. Ming C. Wu [email protected] 511 Sutardja Dai Hall (SDH) Amplifier Frequency Response: Lower and Upper Cutoff Frequency • Midband gain Amid and upper and lower cutoff frequencies ωH and ω L that define bandwidth of an amplifier are often of more interest than the complete transferfunction • Coupling and bypass capacitors(~ F) determineω L • Transistor (and stray) capacitances(~ pF) determineω H Lower Cutoff Frequency (ωL) Approximation: Short-Circuit Time Constant (SCTC) Method 1. Identify all coupling and bypass capacitors 2. Pick one capacitor ( ) at a time, replace all others with short circuits 3. Replace independent voltage source withshort , and independent current source withopen 4. Calculate the resistance ( ) in parallel with 5. Calculate the time constant, 6. Repeat this for each of n the capacitor 7. The low cut-off frequency can be approximated by n 1 ωL ≅ ∑ i=1 RiSCi Note: this is an approximation. The real low cut-off is slightly lower Lower Cutoff Frequency (ωL) Using SCTC Method for CS Amplifier SCTC Method: 1 n 1 fL ≅ ∑ 2π i=1 RiSCi For the Common-Source Amplifier: 1 # 1 1 1 & fL ≅ % + + ( 2π $ R1SC1 R2SC2 R3SC3 ' Lower Cutoff Frequency (ωL) Using SCTC Method for CS Amplifier Using the SCTC method: For C2 : = + = + 1 " 1 1 1 % R3S R3 (RD RiD ) R3 (RD ro ) fL ≅ $ + + ' 2π # R1SC1 R2SC2 R3SC3 & For C1: R1S = RI +(RG RiG ) = RI + RG For C3 : 1 R2S = RS RiS = RS gm Design: How Do We Choose the Coupling and Bypass Capacitor Values? • Since the impedance of a capacitor increases with decreasing frequency, coupling/bypass capacitors reduce amplifier gain at low frequencies. -
T/HIS 15.0 User Manual
For help and support from Oasys Ltd please contact: UK The Arup Campus Blythe Valley Park Solihull B90 8AE United Kingdom Tel: +44 121 213 3399 Email: [email protected] China Arup 39/F-41/F Huaihai Plaza 1045 Huaihai Road (M) Xuhui District Shanghai 200031 China Tel: +86 21 3118 8875 Email: [email protected] India Arup Ananth Info Park Hi-Tec City Madhapur Phase-II Hyderabad 500 081, Telangana India Tel: +91 40 44369797 / 98 Email: [email protected] Web:www.arup.com/dyna or contact your local Oasys Ltd distributor. LS-DYNA, LS-OPT and LS-PrePost are registered trademarks of Livermore Software Technology Corporation User manual Version 15.0, May 2018 T/HIS 0 Preamble 0.1 Text conventions used in this manual 0.1 1 Introduction 1.1 1.1 Program Limits 1.1 1.2 Running T/HIS 1.2 1.3 Command Line Options 1.4 2 Using Screen Menus 2.1 2.1 Basic screen menu layout 2.1 2.2 Mouse and keyboard usage for screen-menu interface 2.2 2.3 Dialogue input in the screen menu interface 2.4 2.4 Window management in the screen interface 2.4 2.5 Dynamic Viewing (Using the mouse to change views). 2.5 2.6 "Tool Bar" Options 2.6 3 Graphs and Pages 3.1 3.1 Creating Graphs 3.1 3.2 Page Size 3.2 3.3 Page Layouts 3.2 3.3.1 Automatic Page Layout 3.2 3.4 Pages 3.6 3.5 Active Graphs 3.6 4 Global Commands and Pages 4.1 4.1 Page Number 4.1 4.2 PLOT (PL) 4.1 4.3 POINT (PT) 4.2 4.4 CLEAR (CL) 4.2 4.5 ZOOM (ZM) 4.2 4.6 AUTOSCALE (AU) 4.2 4.7 CENTRE (CE) 4.2 4.8 MANUAL 4.2 4.9 STOP 4.2 4.10 TIDY 4.2 4.11 Additional Commands 4.3 5 Main Menu 5.1 5.0 Selecting Curves -
Classic Filters There Are 4 Classic Analogue Filter Types: Butterworth, Chebyshev, Elliptic and Bessel. There Is No Ideal Filter
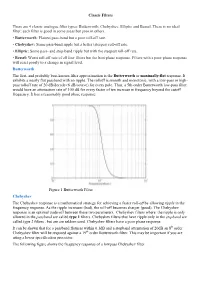
Classic Filters There are 4 classic analogue filter types: Butterworth, Chebyshev, Elliptic and Bessel. There is no ideal filter; each filter is good in some areas but poor in others. • Butterworth: Flattest pass-band but a poor roll-off rate. • Chebyshev: Some pass-band ripple but a better (steeper) roll-off rate. • Elliptic: Some pass- and stop-band ripple but with the steepest roll-off rate. • Bessel: Worst roll-off rate of all four filters but the best phase response. Filters with a poor phase response will react poorly to a change in signal level. Butterworth The first, and probably best-known filter approximation is the Butterworth or maximally-flat response. It exhibits a nearly flat passband with no ripple. The rolloff is smooth and monotonic, with a low-pass or high- pass rolloff rate of 20 dB/decade (6 dB/octave) for every pole. Thus, a 5th-order Butterworth low-pass filter would have an attenuation rate of 100 dB for every factor of ten increase in frequency beyond the cutoff frequency. It has a reasonably good phase response. Figure 1 Butterworth Filter Chebyshev The Chebyshev response is a mathematical strategy for achieving a faster roll-off by allowing ripple in the frequency response. As the ripple increases (bad), the roll-off becomes sharper (good). The Chebyshev response is an optimal trade-off between these two parameters. Chebyshev filters where the ripple is only allowed in the passband are called type 1 filters. Chebyshev filters that have ripple only in the stopband are called type 2 filters , but are are seldom used. -

Feedback Amplifiers
UNIT II FEEDBACK AMPLIFIERS & OSCILLATORS FEEDBACK AMPLIFIERS: Feedback concept, types of feedback, Amplifier models: Voltage amplifier, current amplifier, trans-conductance amplifier and trans-resistance amplifier, feedback amplifier topologies, characteristics of negative feedback amplifiers, Analysis of feedback amplifiers, Performance comparison of feedback amplifiers. OSCILLATORS: Principle of operation, Barkhausen Criterion, types of oscillators, Analysis of RC-phase shift and Wien bridge oscillators using BJT, Generalized analysis of LC Oscillators, Hartley and Colpitts’s oscillators with BJT, Crystal oscillators, Frequency and amplitude stability of oscillators. 1.1 Introduction: Feedback Concept: Feedback: A portion of the output signal is taken from the output of the amplifier and is combined with the input signal is called feedback. Need for Feedback: • Distortion should be avoided as far as possible. • Gain must be independent of external factors. Concept of Feedback: Block diagram of feedback amplifier consist of a basic amplifier, a mixer (or) comparator, a sampler, and a feedback network. Figure 1.1 Block diagram of an amplifier with feedback A – Gain of amplifier without feedback. A = X0 / Xi Af – Gain of amplifier with feedback.Af = X0 / Xs β – Feedback ratio. β = Xf / X0 X is either voltage or current. 1.2 Types of Feedback: 1. Positive feedback 2. Negative feedback 1.2.1 Positive Feedback: If the feedback signal is in phase with the input signal, then the net effect of feedback will increase the input signal given to the amplifier. This type of feedback is said to be positive or regenerative feedback. Xi=Xs+Xf Af = = = Af= Here Loop Gain: The product of open loop gain and the feedback factor is called loop gain. -

Unit I Microwave Transmission Lines
UNIT I MICROWAVE TRANSMISSION LINES INTRODUCTION Microwaves are electromagnetic waves with wavelengths ranging from 1 mm to 1 m, or frequencies between 300 MHz and 300 GHz. Apparatus and techniques may be described qualitatively as "microwave" when the wavelengths of signals are roughly the same as the dimensions of the equipment, so that lumped-element circuit theory is inaccurate. As a consequence, practical microwave technique tends to move away from the discrete resistors, capacitors, and inductors used with lower frequency radio waves. Instead, distributed circuit elements and transmission-line theory are more useful methods for design, analysis. Open-wire and coaxial transmission lines give way to waveguides, and lumped-element tuned circuits are replaced by cavity resonators or resonant lines. Effects of reflection, polarization, scattering, diffraction, and atmospheric absorption usually associated with visible light are of practical significance in the study of microwave propagation. The same equations of electromagnetic theory apply at all frequencies. While the name may suggest a micrometer wavelength, it is better understood as indicating wavelengths very much smaller than those used in radio broadcasting. The boundaries between far infrared light, terahertz radiation, microwaves, and ultra-high-frequency radio waves are fairly arbitrary and are used variously between different fields of study. The term microwave generally refers to "alternating current signals with frequencies between 300 MHz (3×108 Hz) and 300 GHz (3×1011 Hz)."[1] Both IEC standard 60050 and IEEE standard 100 define "microwave" frequencies starting at 1 GHz (30 cm wavelength). Electromagnetic waves longer (lower frequency) than microwaves are called "radio waves". Electromagnetic radiation with shorter wavelengths may be called "millimeter waves", terahertz radiation or even T-rays. -

Wave Guides & Resonators
UNIT I WAVEGUIDES & RESONATORS INTRODUCTION Microwaves are electromagnetic waves with wavelengths ranging from 1 mm to 1 m, or frequencies between 300 MHz and 300 GHz. Apparatus and techniques may be described qualitatively as "microwave" when the wavelengths of signals are roughly the same as the dimensions of the equipment, so that lumped-element circuit theory is inaccurate. As a consequence, practical microwave technique tends to move away from the discrete resistors, capacitors, and inductors used with lower frequency radio waves. Instead, distributed circuit elements and transmission-line theory are more useful methods for design, analysis. Open-wire and coaxial transmission lines give way to waveguides, and lumped-element tuned circuits are replaced by cavity resonators or resonant lines. Effects of reflection, polarization, scattering, diffraction, and atmospheric absorption usually associated with visible light are of practical significance in the study of microwave propagation. The same equations of electromagnetic theory apply at all frequencies. While the name may suggest a micrometer wavelength, it is better understood as indicating wavelengths very much smaller than those used in radio broadcasting. The boundaries between far infrared light, terahertz radiation, microwaves, and ultra-high-frequency radio waves are fairly arbitrary and are used variously between different fields of study. The term microwave generally refers to "alternating current signals with frequencies between 300 MHz (3×108 Hz) and 300 GHz (3×1011 Hz)."[1] Both IEC standard 60050 and IEEE standard 100 define "microwave" frequencies starting at 1 GHz (30 cm wavelength). Electromagnetic waves longer (lower frequency) than microwaves are called "radio waves". Electromagnetic radiation with shorter wavelengths may be called "millimeter waves", terahertz Page 1 radiation or even T-rays. -

Waveguides Waveguides, Like Transmission Lines, Are Structures Used to Guide Electromagnetic Waves from Point to Point. However
Waveguides Waveguides, like transmission lines, are structures used to guide electromagnetic waves from point to point. However, the fundamental characteristics of waveguide and transmission line waves (modes) are quite different. The differences in these modes result from the basic differences in geometry for a transmission line and a waveguide. Waveguides can be generally classified as either metal waveguides or dielectric waveguides. Metal waveguides normally take the form of an enclosed conducting metal pipe. The waves propagating inside the metal waveguide may be characterized by reflections from the conducting walls. The dielectric waveguide consists of dielectrics only and employs reflections from dielectric interfaces to propagate the electromagnetic wave along the waveguide. Metal Waveguides Dielectric Waveguides Comparison of Waveguide and Transmission Line Characteristics Transmission line Waveguide • Two or more conductors CMetal waveguides are typically separated by some insulating one enclosed conductor filled medium (two-wire, coaxial, with an insulating medium microstrip, etc.). (rectangular, circular) while a dielectric waveguide consists of multiple dielectrics. • Normal operating mode is the COperating modes are TE or TM TEM or quasi-TEM mode (can modes (cannot support a TEM support TE and TM modes but mode). these modes are typically undesirable). • No cutoff frequency for the TEM CMust operate the waveguide at a mode. Transmission lines can frequency above the respective transmit signals from DC up to TE or TM mode cutoff frequency high frequency. for that mode to propagate. • Significant signal attenuation at CLower signal attenuation at high high frequencies due to frequencies than transmission conductor and dielectric losses. lines. • Small cross-section transmission CMetal waveguides can transmit lines (like coaxial cables) can high power levels. -

Comparison of a Low-Frequency Butterworth Filter with a Symmetric SE-Filter
Comparison of a low-frequency Butterworth filter with a symmetric SE-filter K S Medvedeva1 1Saratov State University, Astrakhanskaya Street 83, Saratov, Russia, 410012 Abstract. The article compares two filters: a Butterworth filter and an asymmetric SE- filter.The experimental studydetermines their advantages and disadvantages.Also,experiments based on the peak signal-to-noise ratio(PSNR) metricshowvisual evaluation. The results of experimentsshow that a symmetric filter better restores images usinga small set of continuous function parametersthatare distorted by a low-frequency Gaussian filter. 1. Introduction Due to the imperfection of forming and recording systems, images recorded by systemsare distorted (fuzzy) copiesof the original images. The main causes of distortions that resultindegradation of clarity includethe limited resolution of the forming system, refocusing, the presence of a distorting medium (for example, the atmosphere), and movement of the camera on the object being registered. Eliminating or reducing distortion for clarity is the task of image recovery. Automatic control systems, measuring equipment, signal processing systems, and various filters with different characteristics are used to filter signalsin telecommunications. Depending on the frequency band associated with the bandwidth and the suppression band, there are odd, band, high- frequency, and low-frequency filters. Also, all-pass filters have a constant amplitude-frequency response in the required frequency range, and their phase-frequency response is a given frequency function [1]. The simplest way to restoreimage clarity is to process the observed image in the spatial frequency domain with an inverse filter [2].The drawbacks of this filter are the occurrence of edge effects, which take the form of an oscillating hindrance of high power that completely masksthe reconstructed image. -

Introduction to Signals & Systems
A very Brief Introduction to Signals & Systems Outline • Signals & Systems • Continuous and discrete time signals • Properties of Systems • Input- Output relation : Convolution • Frequency domain representation of signals & systems • Analog to digital Conversion • Sampling – Nyquist Sampling Theorem • Basic Filter Theory • Types of filters • Designing practical filters in Labview and Matlab • What is a signal? – A signal is a function defined on the continuum of time values • What is a system ? – a system is a black box that “takes in” one or more input signals and “produces” one or more output signals Continuous time Vs Discrete time Signals • Most of the modern day systems are discrete time systems. E.g., A computer. • A computer can’t directly process a continuous time signal but instead it needs a stream of numbers, which is a discrete time signal. • Discrete time signals are obtain by sampling the continuous time signals • How fast should we sample the signal? Examples • Signals – Unit Step function – Continuous time impulse function – Discrete time • Systems – A simple circuit Basic System Properties • Linearity – System is linear if the principle of superposition holds • Time- Invariance – The system does not change with time Convolution • Linear & Time invariant (LTI) sytems are characterized by their impulse response • Impulse response is the output of the system when the input to the system is an impulse function • For Continuous time signals • For Discrete time signals Frequency domain representation of signals • In most of -

Lab 4: Prelab
ECE 445 Biomedical Instrumentation rev 2012 Lab 8: Active Filters for Instrumentation Amplifier INTRODUCTION: In Lab 6, a simple instrumentation amplifier was implemented and tested. Lab 7 expanded upon the instrumentation amplifier by improving circuit performance and by building a LabVIEW user interface. This lab will complete the design of your biomedical instrument by introducing a filter into the circuit. REQUIRED PARTS AND MATERIALS: Materials Needed 1) Instrumentation amplifier from Lab 7 2) Results from Prelab 3) Oscilloscope 4) Function Generator 5) DC Power Supply 6) Labivew Software 7) Data Acquisition Board 8) Resistors 9) Capacitors 10) Dual operational amplifier (UA747) PRELAB: 1. Print the Prelab and Lab8 Grading Sheets. Answer all of the questions in the Prelab Grading Sheet and bring the Lab8 Grading Sheet with you when you come to lab. The Prelab Grading Sheet must be turned in to the TA before beginning your lab assignment. 2. Read the LABORATORY PROCEDURE before coming to lab. Note: you are not required to print the lab procedure; you can view it on the PC at your lab bench. 3. For further reading consult class notes, text book and see Low Pass Filters http://www.electronics-tutorials.ws/filter/filter_2.html High Pass Filters http://www.electronics-tutorials.ws/filter/filter_3.html BACKGROUND: Active Filters As their name implies, Active Filters contain active components such as operational amplifiers or transistors within their design. They draw their power from an external power source and use it to boost or amplify the output signal. Operational amplifiers can also be used to shape or alter the frequency response of the circuit by producing a more selective output response by making the output bandwidth of the filter more narrow or even wider. -

DETERMINATION of the APPROPRIATE CUTOFF FREQUENCY in the DIGITAL FILTER DATA SMOOTHING PROCEDURE By
'DETERMINATION OF THE APPROPRIATE CUTOFF FREQUENCY IN THE DIGITAL FILTER DATA SMOOTHING PROCEDURE by BING YU B.S., Peking Institute of Physical Education, 1982 A MASTER'S THESIS Submitted in partial fulfillment of the requirements for the degree MASTER OF SCIENCE Department of Physical Education and Leisure Studies KANSAS STATE UNIVERSITY 1988 Approved by: Major Professo 3# AllSDfl 5327b7 ']cl ACKNOWLEDGEMENTS The author wishes to acknowledge the assistance and support of the entire graduate faculty of Kansas State University's Department of Physical Education and Leisure Studies. Special thanks go to committee members Dr. Stephan Konz and Dr. Kathleen Williams for their unique perspectives and editorial assistance. Most of all, I would like to thank my major professor, Dr. Larry Noble, for his integrity, his enthusiasm for knowledge, and the tremendous amount of time and assistance he has given me over the past two years. 11 DEDICATION This thesis is dedicated to my parents, Dr. Gou-Rei Yu and Ming-Hua Lu, to my wife Wei Li, to her parents, Dr. Ping Li and Dr. Xiu-Zhang Yu, and to all of the other folks of my family and her family for their understanding of my absence when my son Charlse Alan Yu was born. Their constant support and encouragement are deeply appreciated. 111 . CONTENTS ACKNOWLEDGMENTS ii DEDICATION iii LIST OF FIGURES vi LIST OF TABLES ix Chapter 1 INTRODUCTION 1 Statement Of The Problem 2 Definitions 3 2 REVIEW OF RELATED LITERATURE 7 The Nature Of Errors 7 Sources Of Errors 10 Data Smoothing Techniques Used In Sport Biomechanics 15 Finite difference technique 15 Least square polynomial approxination.