Impedance of Small-Angle Collimators in High-Frequency Limit Abstract
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Design and Testing of Collimators for Use in Measuring X-Ray Attenuation
DESIGN AND TESTING OF COLLIMATORS FOR USE IN MEASURING X-RAY ATTENUATION By RAJESH PANTHI Master of Science (M.Sc.) in Physics Tribhuvan University Kathmandu, Nepal 2009 Submitted to the Faculty of the Graduate College of the Oklahoma State University in partial fulfillment of the requirements for the Degree of MASTER OF SCIENCE December, 2017 DESIGN AND TESTING OF COLLIMATORS FOR USE IN MEASURING X-RAY ATTENUATION Thesis Approved: Dr. Eric R. Benton Thesis Adviser and Chair Dr. Eduardo G. Yukihara Dr. Mario F. Borunda ii ACKNOWLEDGEMENTS I would like to express the deepest appreciation to my thesis adviser As- sociate Professor Dr. Eric Benton of the Department of Physics at Oklahoma State University for his vigorous guidance and help in the completion of this work. He provided me all the academic resources, an excellent lab environment, financial as- sistantship, and all the lab equipment and materials that I needed for this project. I am grateful for many skills and knowledge that I gained from his classes and personal discussion with him. I would like to thank Adjunct Profesor Dr. Art Lucas of the Department of Physics at Oklahoma State University for guiding me with his wonderful experience on the Radiation Physics. My sincere thank goes to the members of my thesis committee: Professor Dr. Eduardo G. Yukihara and Assistant Professor Dr. Mario Borunda of the Department of Physics at Oklahoma State University for generously offering their valuable time and support throughout the preparation and review of this document. I would like to thank my colleague Mr. Jonathan Monson for helping me to access the Linear Accelerators (Linacs) in St. -

ADVANCED SPECTROMETER Introduction
ADVANCED SPECTROMETER Introduction In principle, a spectrometer is the simplest of scientific very sensitive detection and precise measurement, a real instruments. Bend a beam of light with a prism or diffraction spectrometer is a bit more complicated. As shown in Figure grating. If the beam is composed of more than one color of 1, a spectrometer consists of three basic components; a light, a spectrum is formed, since the various colors are collimator, a diffracting element, and a telescope. refracted or diffracted to different angles. Carefully measure The light to be analyzed enters the collimator through a the angle to which each color of light is bent. The result is a narrow slit positioned at the focal point of the collimator spectral "fingerprint," which carries a wealth of information lens. The light leaving the collimator is therefore a thin, about the substance from which the light emanates. parallel beam, which ensures that all the light from the slit In most cases, substances must be hot if they are to emit strikes the diffracting element at the same angle of inci- light. But a spectrometer can also be used to investigate cold dence. This is necessary if a sharp image is to be formed. substances. Pass white light, which contains all the colors of The diffracting element bends the beam of light. If the beam the visible spectrum, through a cool gas. The result is an is composed of many different colors, each color is dif- absorption spectrum. All the colors of the visible spectrum fracted to a different angle. are seen, except for certain colors that are absorbed by the gas. -

Lhc Collimator Alignment Operational Tool∗
TUPPC120 Proceedings of ICALEPCS2013, San Francisco, CA, USA LHC COLLIMATOR ALIGNMENT OPERATIONAL TOOL∗ G. Valentinoy , CERN, Geneva, Switzerland and University of Malta, Msida, Malta R. W. Aßmannz , S. Redaelli, CERN, Geneva, Switzerland N. Sammut, University of Malta, Msida, Malta Abstract tor tanks housing the jaws and other equipment such as Beam-based LHC collimator alignment is necessary to quadrupole magnets and Beam Position Monitors (BPMs). determine the beam centers and beam sizes at the colli- The actual beam orbit may deviate from the design orbit mator locations for various machine configurations. Fast over several months of operation due to ground motion and and automatic alignment is provided through an opera- thermal effects [4]. Hence, all collimators are periodically tional tool has been developed for use in the CERN Con- aligned to the beam to determine these parameters. A jaw trol Center, which is described in this paper. The tool is is aligned when a sharp increase followed by a slow expo- implemented as a Java application, and acquires beam loss nential decrease appears in the signal read out from a Beam and collimator position data from the hardware through a Loss Monitoring (BLM) detector [5] placed downstream of middleware layer. The user interface is designed to allow the collimator. for a quick transition from application start up, to select- ing the required collimators for alignment and configuring OPERATIONAL TOOL the alignment parameters. The measured beam centers and Main Display sizes are then logged and displayed in different forms to A screenshot of the main display of the collimator appli- help the user set up the system. -

Evaluation of Infrared Collimators for Testing Thermal Imaging Systems
OPTO-ELECTRONICS REVIEW 15(2), 82–87 DOI: 10.2478/s11772-007-0005-9 Evaluation of infrared collimators for testing thermal imaging systems K. CHRZANOWSKI*1,2 1Institute of Optoelectronics, Military University of Technology, 2 Kaliskiego Str., 00-908 Warsaw, Poland 2INFRAMET, 24 Graniczna Str., Kwirynów, 05-082 Stare Babice, Poland Infrared reflective collimators are important components of expensive sophisticated test systems used for testing thermal imagers. Too low quality collimators can become a source of significant measurement errors and collimators of too high quality can unnecessarily increase cost of a test system. In such a situation it is important for test system users to know proper requirements on the collimator and to be able to verify its performance. A method for evaluation of infrared reflective collimators used in test systems for testing thermal imagers is presented in this paper. The method requires only easily avail- able optical equipment and can be used not only by collimator manufactures but also by users of test equipment to verify per- formance of the collimators used for testing thermal imagers. Keywords: IR systems, testing thermal imaging systems, IR optical design. 1. Introduction requirement that the collimator spatial resolution should match the spatial resolution capabilities of the tested thermal IR collimators are typical elements of laboratory sets-up used imager. for testing thermal imaging systems. Reflective two-mirror Although IR collimators are frequently used for testing collimators built using an off-axis parabolic collimating mir- thermal imagers since the 1970s, there has been little interest ror and smaller directional flat mirror represent a typical de- in a problem of evaluation of these optical systems. -

Super-Collimation in a Rod-Based Photonic Crystal by Ta-Ming Shih B.S
Super-collimation in a Rod-based Photonic Crystal by Ta-Ming Shih B.S. Electrical Engineering and Computer Science University of California, Berkeley 2006 Submitted to the Department of Electrical Engineering and Computer Science in partial ful¯llment of the requirements for the degree of Master of Science in Electrical Engineering at the MASSACHUSETTS INSTITUTE OF TECHNOLOGY September 2007 °c Massachusetts Institute of Technology 2007. All rights reserved. Author.............................................................. Ta-Ming Shih Department of Electrical Engineering and Computer Science August 20, 2007 Certi¯ed by. Leslie A. Kolodziejski Professor of Electrical Engineering and Computer Science Thesis Supervisor Accepted by . Arthur C. Smith Chair, Department Committee on Graduate Students 2 Super-collimation in a Rod-based Photonic Crystal by Ta-Ming Shih Submitted to the Department of Electrical Engineering and Computer Science on August 20, 2007, in partial ful¯llment of the requirements for the degree of Master of Science in Electrical Engineering Abstract Super-collimation is the propagation of a light beam without spreading that occurs when the light beam is guided by the dispersion properties of a photonic crystal, rather than by defects in the photonic crystal. Super-collimation has many potential applications, the most straight-forward of which is in the area of integrated optical circuits, where super-collimation can be utilized for optical routing and optical logic. Another interesting direction is the burgeoning ¯eld of optofluidics, in which inte- grated biological or chemical sensors can be based on super-collimating structures. The work presented in the thesis includes the design, fabrication, and characteriza- tion of a rod-based two-dimensional photonic crystal super-collimator. -

Novel Fiber Fused Lens for Advanced Optical Communication Systems Andrew A
Novel Fiber Fused Lens for Advanced Optical Communication Systems Andrew A. Chesworth*a, Randy K. Rannow b, Omar Ruiz a, Matt DeRemer a, Joseph Leite a, Armando Martinez b, Dustin Guenther b aLightPath Technology, 2603 Challenger Tech Ct., Orlando, FL, 32826, USA bAPIC Corporation, 5800 Uplander Way, Los Angeles, CA, 90230, USA ABSTRACT We report on a novel fused collimator design as part of a transmitter optical sub-assembly (TOSA) used for agile microwave photonic links. The fused collimator consists of a PM fiber that is laser fused to a C type lens. The fusion joint provides a low loss interface between the two components and eliminates the need for separate components in the optical path. The design simplifies the number of components with the optical assembly leading to several advantages over traditional designs. In this paper we use the fiber coupling efficiency as a design metric and discuss the opt- mechanical tolerances and its effect on the overall design parameters. Keywords: Fiber Collimators, Fiber Coupling, RF Photonic Links, TOSA 1. INTRODUCTION Recent advances in the development of high power 1550nm semiconductor lasers for agile microwave photonic links have created a demand for high performance, reliable and robust beam delivery optics. In this paper we describe a transmitter optical sub-assembly (TOSA) based on a novel collimator design. The basic elements of the TOSA are the laser source, precision molded asphere, isolator, focusing lens and PM fiber. Traditionally, the focusing lens and fiber are discrete elements. In this application, the focusing lens and optical fiber are fused together to produce a single element referred to as a collimator (although in this application it’s used as a coupler). -

Movable Collimator System for Superkekb
PHYSICAL REVIEW ACCELERATORS AND BEAMS 23, 053501 (2020) Movable collimator system for SuperKEKB T. Ishibashi , S. Terui, Y. Suetsugu, K. Watanabe, and M. Shirai High Energy Accelerator Research Organization (KEK), 305-0801, Tsukuba, Japan (Received 3 March 2020; accepted 6 May 2020; published 13 May 2020) Movable collimators for the SuperKEKB main ring, which is a two-ring collider consisting of a 4 GeV positron and 7 GeVelectron storage ring, were designed to fit an antechamber scheme in the beam pipes, to suppress background noise in a particle detector complex named Belle II, and to avoid quenches, derived from stray particles, in the superconducting final focusing magnets. We developed horizontal and vertical collimators having a pair of horizontally or vertically opposed movable jaws with radiofrequency shields. The collimators have a large structure that protrudes into the circulating beam and a large impedance. Therefore, we estimated the impedance using an electromagnetic field simulator, and the impedance of the newly developed collimators is lower compared with that of our conventional ones because a part of each movable jaw is placed inside the antechamber structure. Ten horizontal collimators and three vertical collimators were installed in total, and we installed them in the rings taking the phase advance to the final focusing magnets into consideration. The system generally functioned, as expected, at a stored beam current of up to approximately 1 A. In high-current operations at 500 mA or above, the jaws were occasionally damaged by hitting abnormal beams, and we estimated the temperature rise for the collimator’s materials using a Monte Carlo simulation code. -

Chapter 5: X-Ray Production
Chapter 5: X-Ray Production Slide set of 121 slides based on the chapter authored by R. Nowotny of the IAEA publication (ISBN 978-92-0-131010-1): Diagnostic Radiology Physics: A Handbook for Teachers and Students Objective: To familiarize the student with the principles of X ray production and the characterization of the radiation output of X ray tubes. Slide set prepared by K.P. Maher following initial work by S. Edyvean IAEA International Atomic Energy Agency CHAPTER 5 TABLE OF CONTENTS 5.1 Introduction 5.2 Fundamentals of X Ray Production 5.3 X Ray Tubes 5.4 Energizing & Controlling the X Ray Tube 5.5 X Ray Tube & Generator Ratings 5.6 Collimation & Filtration 5.7 Factors Influencing X Ray Spectra & Output 5.8 Filtration Bibliography IAEA Diagnostic Radiology Physics: a Handbook for Teachers and Students – chapter 5, 2 CHAPTER 5 TABLE OF CONTENTS 5.1 Introduction 5.2 Fundamentals of X Ray Production 5.2.1 Bremsstrahlung 5.2.2 Characteristic Radiation 5.2.3 X Ray Spectrum 5.3 X Ray Tubes 5.3.1 Components of the X Ray Tube 5.3.2 Cathode 5.3.3 Anode 5.3.3.1 Choice of material 5.3.3.2 Line-Focus principle (Anode angle) 5.3.3.3 Stationary and rotating anodes 5.3.3.4 Thermal properties 5.3.3.5 Tube envelope IAEA 5.3.3.6 Tube housing Diagnostic Radiology Physics: a Handbook for Teachers and Students – chapter 5, 3 CHAPTER 5 TABLE OF CONTENTS 5.4 Energizing & Controlling the X-Ray Tube 5.4.1 Filament Circuit 5.4.2 Generating the Tube Voltage 5.4.2.1 Single-phase generators 5.4.2.2 Three-phase generators 5.4.2.3 High-frequency generators 5.4.2.4 -

Chapter 5 TREATMENT MACHINES for EXTERNAL BEAM
Chapter 5 TREATMENT MACHINES FOR EXTERNAL BEAM RADIOTHERAPY E.B. PODGORSAK Department of Medical Physics, McGill University Health Centre, Montreal, Quebec, Canada 5.1. INTRODUCTION Since the inception of radiotherapy soon after the discovery of X rays by Roentgen in 1895, the technology of X ray production has first been aimed towards ever higher photon and electron beam energies and intensities, and more recently towards computerization and intensity modulated beam delivery. During the first 50 years of radiotherapy the technological progress was relatively slow and mainly based on X ray tubes, van de Graaff generators and betatrons. The invention of the 60Co teletherapy unit by H.E. Johns in Canada in the early 1950s provided a tremendous boost in the quest for higher photon energies and placed the cobalt unit at the forefront of radiotherapy for a number of years. The concurrently developed medical linacs, however, soon eclipsed cobalt units, moved through five increasingly sophisticated generations and became the most widely used radiation source in modern radiotherapy. With its compact and efficient design, the linac offers excellent versatility for use in radiotherapy through isocentric mounting and provides either electron or megavoltage X ray therapy with a wide range of energies. In addition to linacs, electron and X ray radiotherapy is also carried out with other types of accelerator, such as betatrons and microtrons. More exotic particles, such as protons, neutrons, heavy ions and negative p mesons, all produced by special accelerators, are also sometimes used for radiotherapy; however, most contemporary radiotherapy is carried out with linacs or teletherapy cobalt units. -

Partial Collimation of Diffuse Light from a Diffusely Reflective Source Lakes
1 Partial collimation of diffuse light from a diffusely reflective source Lakes, R. S. and Vick, G., "Partial collimation of light from a diffusely reflective source", adapted from J. Modern Optics, 39, 2113- 2119, (1992). Abstract A general purpose collimator capable of collimation of radiation from an arbitrary thermal source of diffuse light is incompatible with the second law of thermodynamics. It is known, however, that diffusion of coherent light from a particular ground glass can be reversed holographically. A new collimator is presented which produces a partially collimated beam of increased radiance when placed close to a white (diffusely reflective) source. 1. Introduction Light can be readily diffused by a ground glass or other scattering medium, but the inverse process of collimating diffuse light is not as readily accomplished. A simple light baffle can reject the oblique rays, leaving only the ones in a desired range of directions, at the expense of much loss of light; such a baffle does not collimate the light since no rays are redirected. One may envisage holographic Bragg planes which diffract oblique rays into the direction normal to the plate, but such Bragg planes also diffract the normal rays in an oblique direction, so that no collimation is achieved. In this article we examine conditions under which collimation of diffuse light is possible, present a design for such a collimator, and present experimental results. 2. Limitations associated with the second law of thermodynamics A collimator for a diffuse source will transform a disordered system into a more ordered one. Consequently limitations associated with the second law of thermodynamics are to be considered. -

(Light Emitting Diode) To
GENERAL DATA: Parts No. HS403GL UPC: 760921087503 Principle Reflex collimator sight - red dot sight OPTICAL DATA: Light source LED (Light Emitting Diode) totally eye-safe wavelength: 650 nm red light Red Dot Size 2 MOA -- 1 minute of angle = 30mm at 100 meters / 1.04 inch at 100 yards Parallax Parallax free: No centering required, aim with red dot anywhere inside window. Eye Relief Unlimited 2 brightness settings for night version. Settings 1, 2 are for night vision. From setting 3 to Night Vision 12 are day time setting from dim to bright. Coating Multi-layer coating on all lenses magnification 1X ELECTRONIC DATA: Battery CR2032 50,000 hours. Based on setting 6. current is 5μA (micro Ampere). The battery capacity is Battery Life 250mAHour. 250mAHoursX1000/5μA=50,000 hours Auto Shutoff 8 Hours. After sight is not used for 8 hours, it will automatically shutoff. 12 brightness setting include 2 night vision settings. all setting current reading(from 12 to Setting 1) 179μA 36μA 22μA 13.1μA 8.8μA 5.91μA 4.92μA 4.53μA 4.25μA 4.13μA 4.06μA 4.02μA MECHANICAL DATA: Housing Material Aluminum 6061-T6 PEO/MAO housing finish: Plasma electrolytic oxidation (PEO), also known as micro-arc oxidation (MAO), is an electrochemical surface treatment process for generating oxide coatings on metals. It is similar to anodizing, but it employs higher potentials, so that discharges occur and the resulting plasma modifies the structure of the oxide layer. This Housing Finish process can be used to grow thick (tens or hundreds of micrometers), largely crystalline, oxide coatings on metals such as aluminium, magnesium and titanium. -
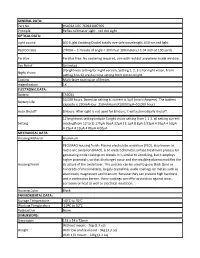
Part No. HS403A UPC 760921087305 Principle Reflex Collimator Sight
GENERAL DATA: Part No. HS403A UPC 760921087305 Principle Reflex collimator sight - red dot sight OPTICAL DATA: Light source LED (Light Emitting Diode) totally eye-safe wavelength: 650 nm red light Red Dot Size 2 MOA -- 1 minute of angle = 30mm at 100 meters / 1.04 inch at 100 yards Parallax Parallax free: No centering required, aim with red dot anywhere inside window. Eye Relief Unlimited 3 brightness setting for night version, Setting 1, 2, 3 is for night vision, From Night Vision setting 4 to 12 are day time setting from dim to bright. Coating Multi-layer coating on all lenses magnification 1X ELECTRONIC DATA: Battery CR2032 50,000 hours. Based on setting 6. current is 5μA (micro Ampere). The battery Battery Life capacity is 250mAHour. 250mAHoursX1000/5μA=50,000 hours Auto Shutoff 8 Hours. After sight is not used for 8 hours, it will automatically shutoff. 12 brightness setting include 3 night vision setting from 1 2 3. all setting current Setting reading(from 12 to 1) 179μA 36μA 22μA 13.1μA 8.8μA 5.91μA 4.92μA 4.53μA 4.25μA 4.13μA 4.06μA 4.02μA MECHANICAL DATA: Housing Material Aluminum PEO/MAO housing finish: Plasma electrolytic oxidation (PEO), also known as micro-arc oxidation (MAO), is an electrochemical surface treatment process for generating oxide coatings on metals. It is similar to anodizing, but it employs higher potentials, so that discharges occur and the resulting plasma modifies the Housing Finish structure of the oxide layer. This process can be used to grow thick (tens or hundreds of micrometers), largely crystalline, oxide coatings on metals such as aluminium, magnesium and titanium.