[Physics.Pop-Ph] 3 Oct 1997
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

By Omission and Commission : 'Race'
National Library Bibliothbque nationale 1*1 of Canada du Canada Acquisitions and Direction des acquisitions et Bibliographic Services Branch des services bibliographiques 395 Wellington Street 395, rue Wellington Ottawa, Ontario Ottawa (Ontario) KIA ON4 KIA ON4 Your hie Votre ri2ference Our Me Notre reference The author has granted an L'auteur a accorde une licence irrevocable non-exclusive licence irriivocable et non exclusive allowing the National Library of permettant a la Bibliotheque Canada to reproduce, loan, nationale du Canada de distribute or sell copies of reproduire, prGter, distribuer ou his/her thesis by any means and vendre des copies de sa these in any form or format, making de quelque maniere et sous this thesis available to interested quelque forme que ce soit pour persons. mettre des exemplaires de cette these a la disposition des personnes interessees. The author retains ownership of L'auteur conserve la propriete du the copyright in his/her thesis. droit d'auteur qui protege sa Neither the thesis nor substantial these. Ni la these ni des extraits extracts from it may be printed or substantiels de celle-ci ne otherwise reproduced without doivent &re imprimes ou his/her permission. autrement reproduits sans son autorisation. ISBN 0-315-91241-3 BY OMISSION AND COMMISSION: 'RACE' AND REPRESENTATION IN CANADIAN TELEVISION NEWS by Yasmin Jiwani B.A., University of British Columbia, 1979 M.A., Simon Fraser University, 1984 THESIS SUBMITTED IN PARTIAL FULFILMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY in the Department of Communication @ Yasmin Jiwani 1993 SIMON FRASER UNIVERSITY July, 1993 All rights reserved. -

February 26, 2021 Morning Announcements
February 26, 2021 Black History Month person of note is Donovan Bailey, who is now a retired Jamaican-Canadian athlete who is regarded as the greatest Canadian sprinter of all time. He once held the world record for the 100 metre sprint, recording a time of 9.84 seconds to win the Gold Medal at the 1996 Olympics. Usain Bolt of Jamaica surpassed that record in 2009 with a 100 metre dash of 9.58 seconds. Virtual open house is next Monday, March 1st. If you have a sibling coming to Maples for Grade 9 next year, direct them to our Maples website next Monday for more information about the school and registration. This will not be a live event! Follow us @Maples_Collegiate on Instagram for more information. Are you interested in joining next year’s chamber choir? Maples Chamber Choir is a full credit, timetables course. If you are in Grade 10 or Grade 11 and are in the school today, please come by the choir room at lunch time and pick up information on how to become part of this energetic group of singers. March 1st is a very important deadline date for U of W and U of M: o University of Winnipeg applications are due by March 1st if a student wishes to be considered for the Automatic Special Entrance Scholarship. o University of Manitoba applications are due by March 1st if a student is interested in applying to a Direct Entry Program and if they wish to be considered for the Automatic Entrance Scholarship. Feel free to see Mrs. -

Indoor Track and Field DIVISION I MEN’S
Indoor Track and Field DIVISION I MEN’S Highlights Florida claims top spot in men’s indoor track: At the end of the two-day gamut of ups and downs that is the Division I NCAA Indoor Track and Field National Champion- ships, Florida coach Mike Holloway had a hard time thinking of anything that went wrong for the Gators. “I don’t know,” Holloway said. “The worst thing that happened to me was that I had a stomachache for a couple of days.” There’s no doubt Holloway left the Randal Tyson Track Center feeling better on Saturday night. That’s because a near-fl awless performance by the top-ranked Gators re- sulted in the school’s fi rst indoor national championship. Florida had come close before, fi nishing second three times in Holloway’s seven previous years as head coach. “It’s been a long journey and I’m just so proud of my staff . I’m so proud of my athletes and everybody associated with the program,” Holloway said. “I’m almost at a loss for words; that’s how happy I am. “It’s just an amazing feeling, an absolutely amazing feeling.” Florida began the day with 20 points, four behind host Arkansas, but had loads of chances to score and didn’t waste time getting started. After No. 2 Oregon took the lead with 33 points behind a world-record performance in the heptathlon from Ashton Eaton and a solid showing in the mile, Florida picked up seven points in the 400-meter dash. -

Doping in Sport, the Rules on “Missed Tests”, “Non- Analytical Finding” Cases and the Legal Implications by Gregory Ioannidis*
Doping in Sport, the Rules on “Missed Tests”, “Non- Analytical Finding” Cases and the Legal Implications by Gregory Ioannidis* Much discussion has been generated with the introduction of a new of one or more anti-doping rule violations”. These anti-doping viola- rule to combat the use of performance enhancing substances and tions may incur in situations where the athlete did not use perform- methods in sport. This discussion has been initiated and subsequent- ance enhancing substances, but simply, where he “missed”, “failed” ly became an integral part of the sporting public opinion, as a result and/or “evaded” the test. For the purposes of analysing these rules, we of the application of this rule on high profile professional athletes, would call these specific cases “non-analytical finding” cases. such as the Greek sprinters Kenteris and Thanou. 1 The reason for the examination of the IAAF’s rule, concentrates on Before, however, an analysis of the application of this rule can be the fact that it is attracting intense criticism, in relation to its applica- produced, it is first of all necessary to explain and define the opera- tion on anti-doping violations. In addition, this regulation in ques- tion of the rule and perhaps attempt to discover the reasons for its cre- tion has been associated with high profile cases, and has also become ation. the source of a unique form of questioning. A series of questions arise The article would concentrate on the IAAF’s [International out of its construction, interpretation and application in practice. Association of Athletics Federations] rule on missed tests and critical- These questions cannot be answered without a further examination ly analyse its definition and application, particularly at the charging of the factual issues that surround the application of this regulation. -

P 001 WJ Recs
IAAF WORLD U20 CHAMPIONSHIPS Facts & Figures IAAF World U20 Records .......................................................................................1 IAAF World U20 Championship Records (& Best Performances)..........................3 Summary of Past Championships ..........................................................................5 Superlatives..........................................................................................................16 Placing Tables ......................................................................................................17 Country Index .......................................................................................................20 BYDGOSZCZ 2016 ★ FACTS & FIGURES/WORLD U20 RECORDS 1 IAAF WORLD U20 RECORDS * Awaiting ratification as at July 15, 2016 MEN Wind # = No longer an IAAF World U20 record event, this is the last record to be ratified 100 Metres 9.97 Travyon Bromell USA Eugene 14 Jun 14 1.8 200 Metres 19.93 Usain Bolt JAM Devonshire 11 Apr 04 1.4 400 Metres 43.87 Steve Lewis USA Seoul 28 Sep 88 800 Metres 1:41.73 Nijel Amos BOT London 9 Aug 12 1000 Metres 2:15.00 Benjamin Kipkirui KEN Nice 17 Jul 99 1500 Metres 3:28.81 Ronald Kwemoi KEN Monaco 18 Jul 14 One Mile 3:49.29 William Biwott KEN Oslo 3 Jul 09 (now İlham Tanui Özbilen TUR) 3000 Metres 7:28.78 Augustine Choge KEN Doha 13 May 05 5000 Metres 12:47.53 Hagos Gebrhiwet ETH Paris 6 Jul 12 10,000 Metres 26:41.75 Samuel Wanjiru KEN Bruxelles 26 Aug 05 2000m Steeplechase# 5:25.01 Arsenios Tsiminos GRE Athína 2 -

2011 Ucla Men's Track & Field
2011 MEN’S TRACK & FIELD SCHEDULE IINDOORNDOOR SSEASONEASON Date Meet Location January 28-29 at UW Invitational Seattle, WA February 4-5 at New Balance Collegiate Invitational New York, NY at New Mexico Classic Albuquerque, NM February 11-12 at Husky Classic Seattle, WA February 25-26 at MPSF Indoor Championships Seattle, WA March 5 at UW Final Qualifi er Seattle, WA March 11-12 at NCAA Indoor Championships College Station, TX OOUTDOORUTDOOR SSEASONEASON Date Meet Location March 11-12 at Northridge Invitational Northridge, CA March 18-19 at Aztec Invitational San Diego, CA March 25 vs. Texas & Arkansas Austin, TX April 2 vs. Tennessee ** Drake Stadium April 7-9 Rafer Johnson/Jackie Joyner Kersee Invitational ** Drake Stadium April 14 at Mt. SAC Relays Walnut, CA April 17 vs. Oregon ** Drake Stadium April 22-23 at Triton Invitational La Jolla, CA May 1 at USC Los Angeles, CA May 6-7 at Pac-10 Multi-Event Championships Tucson, AZ May 7 at Oxy Invitational Eagle Rock, CA May 13-14 at Pac-10 Championships Tucson, AZ May 26-27 at NCAA Preliminary Round Eugene, OR June 8-11 at NCAA Outdoor Championships Des Moines, IA ** denotes UCLA home meet TABLE OF CONTENTS/QUICK FACTS QUICK FACTS TABLE OF CONTENTS Location .............................................................................J.D. Morgan Center, GENERAL INFORMATION ..........................................325 Westwood Plaza, Los Angeles, CA, 90095 2011 Schedule .........................Inside Front Cover Athletics Phone ......................................................................(310) -

Final START LIST 200 Metres WOMEN Loppukilpailu OSANOTTAJALUETTELO 200 M NAISET
10th IAAF World Championships in Athletics Helsinki From Saturday 6 August to Sunday 14 August 2005 200 Metres WOMEN 200 m NAISET ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHL Final START LIST Loppukilpailu OSANOTTAJALUETTELO ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETIC ATHLETI 12 August 2005 19:30 START BIB COMPETITOR NAT YEAR Personal Best 2005 Best 1 104 Cydonie MOTHERSILL CAY 78 22.39 22.39 2 784 LaTasha COLANDER USA 76 22.34 22.34 3 32 Kim GEVAERT BEL 78 22.48 22.68 4 779 Rachelle BOONE-SMITH USA 81 22.22 22.22 5 236 Christine ARRON FRA 73 22.26 22.38 6 789 Allyson FELIX USA 85 22.11 22.13 7 398 Veronica CAMPBELL JAM 82 22.05 22.35 8 630 Yuliya GUSHCHINA RUS 83 22.53 22.53 MARK COMPETITOR NAT AGE Record Date Record Venue WR21.34 Florence GRIFFITH-JOYNER USA 2829 Sep 1988 Seoul CR21.74 Silke GLADISCH-MÖLLER GDR 233 Sep 1987 Roma WL22.13 Allyson FELIX USA 1926 Jun 2005 Carson, CA WORLD ALL-TIME / MAAILMAN KAIKKIEN AIKOJEN WORLD TOP 2005 / MAAILMAN 2005 MARK COMPETITOR COUNTRY DATE MARKCOMPETITOR COUNTRY DATE 21.34Florence GRIFFITH-JOYNER USA 29 Sep 88 22.13Allyson FELIX USA 26 Jun 21.62Marion JONES USA 11 Sep 98 22.22Rachelle BOONE-SMITH USA 26 Jun 21.64Merlene OTTEY JAM 13 Sep 91 22.27Lauryn WILLIAMS USA 22 May -

Official Results
DOLCANCUP, VII Europejski Festiwal Lekkoatletyczny 10 czerwca/June 2007 OFFICIAL RESULTS 100 m men/mężczyzn 07-06-10 16:55 RŚ: 9.77 Asafa POWELL Jamaica Ateny 14/06/05 RE: 9.86 Obadele THOMPSOHN POR Athens 22/08/04 Referee: Spasowicz Andrzej RP: 10.00 Marian WORONIN LEGIA Warszawa Warszawa 09/06/84 Place Lane Bib Competitor Year Affiliation Reaction Mark Heat-Bieg 1/1 Wind:+2,1 m/s 1 4 163 Kamil MASZTAK 84 AZS-AWF Poznań(POL) 0.138 10.21 2 6 162 Przemysław ROGOWSKI 80 AZS Poznań(POL) 0.161 10.23 3 5 161 Łukasz CHYŁA 81 SKLA Sopot(POL) 0.177 10.31 4 7 164 Michał BIELCZYK 84 AZS-AWF Warszawa(POL) 0.186 10.35 5 3 167 Radosław DRAPAŁA 86 AZS Poznań(POL) 0.254 10.69 OFFICIAL RESULTS Place Heat/Place Competitor Year Affiliation Mark 1 Heat- 1 Kamil MASZTAK 84 AZS-AWF Poznań 10.21 2 Heat- 2 Przemysław ROGOWSKI 80 AZS Poznań 10.23 3 Heat- 3 Łukasz CHYŁA 81 SKLA Sopot 10.31 4 Heat- 4 Michał BIELCZYK 84 AZS-AWF Warszawa 10.35 5 Heat- 5 Radosław DRAPAŁA 86 AZS Poznań 10.69 100 m men/mężczyzn PK/EH 07-06-10 17:00 RŚ: 9.77 Asafa POWELL Jamaica Ateny 14/06/05 RE: 9.86 Obadele THOMPSOHN POR Athens 22/08/04 Referee: Spasowicz Andrzej RP: 10.00 Marian WORONIN LEGIA Warszawa Warszawa 09/06/84 Place Lane Bib Competitor Year Affiliation Reaction Mark Heat-Bieg 1/1 Wind:+3,5 m/s 1 4 283 Mikołaj LEWAŃSKI 86 MKL Szczecin(POL) 0.131 10.37 2 5 284 Mateusz PLUTA 87 AZS-AWF Kraków(POL) 0.229 10.41 3 3 166 Karol SIENKIEWICZ 86 KS Podlasie Białystok(POL) 0.179 10.44 4 6 287 Fabian ZIÓŁKOWSKI 86 MKL Szczecin(POL) 0.162 10.50 5 7 165 Jacek ROSZKO 87 KS Podlasie Białystok(POL) 0.148 10.52 Personal best with year, season best 2007, WR-world record, ER-european r., NR-national r., MR-meeting r. -

Tyson Invitational Top Ten List
TYSON INVITATIONAL TOP TEN LIST (MEN’S EVENTS) 60 METERS 3000 METERS HIGH JUMP HEPTATHLON 6.46 Terrence Trammell, USA, 2003 7:35.65 Boaz Cheboiywo, Kenya, 2006 2.33m Andra Manson, Texas, 2007 5,826 Terry Prentice, Unattached, 2013 6.48 John Capel, USA, 2003 7:38.30 Boaz Cheboiywo, NIKE, 2004 2.33m Veron Turner, Oklahoma, 2018 5,277 Denim Rogers, Houston Baptist, 2019 6.50 Maurice Greene, USA, 2003 7:38.59 Alistair Cragg, Arkansas, 2004 2.33m Erik Kynard, Kansas State, 2011 4,907 Lane Austell, Unattached, 2013 6.52 Lerone Clarke, Jamaica, 2012 7:40.17 Daniel Lincoln, NIKE, 2004 2.30m Jacorian Duffield, NIKE, 2017 4,276 Daniel Spejcher, Unattached, 2019 6.52 John Teeters, OK State, 2015 (Prelims) 7:40.17 Kevin Sullivan, Reebok, 2007 2.30m Donald Thomas, Auburn, 2007 4,019 Hootie Hurley, Unattached, 2019 6.53 Jon Drummond, Nike, 2000 7:40.25 Matt Tegenkamp, NIKE, 2007 2.29m Bradley Adkins, Texas Tech, 2016 3,789 Kyle Costner, Unattached, 2019 6.54 John Teeters, OK State, 2015 (Semis) 7:40.53 Alistair Cragg, Adidas, 2005 2.28m JuVaughn Harrison, LSU, 2020 3,011 Julius Sommer, Arkansas, 2013 6.54 Maurice Greene, USA, 2003 (Prelims) 7:40.72 Markos Geneti, Adidas, 2005 2.28m Christoff Bryan, Kansas State, 2015 6.54 Terrence Trammell, USA, 2003 (Prelims) 7:41.59 Adam Goucher, USA, 2006 2.27m Marcus Jackson, Miss State, 2014 6.54 Jason Smoots, NIKE, 2005 7:42.17 Kevin Sullivan, Canada, 2006 2.27m Derek Drouin, Indiana, 2011 HEPTATHLON 60M 6.54 Rakieem Salaam, Oklahoma 2011, (Semis) 2.27m Ricky Robertson, Mississippi, 2011 7.01 Terry Prentice, -

Men's 200M Final 23.08.2020
Men's 200m Final 23.08.2020 Start list 200m Time: 17:10 Records Lane Athlete Nat NR PB SB 1 Richard KILTY GBR 19.94 20.34 WR 19.19 Usain BOLT JAM Olympiastadion, Berlin 20.08.09 2 Mario BURKE BAR 19.97 20.08 20.78 AR 19.72 Pietro MENNEA ITA Ciudad de México 12.09.79 3 Felix SVENSSON SWE 20.30 20.73 20.80 NR 20.30 Johan WISSMAN SWE Stuttgart 23.09.07 WJR 19.93 Usain BOLT JAM Hamilton 11.04.04 4 Jan VELEBA CZE 20.46 20.64 20.64 MR 19.77 Michael JOHNSON USA 08.07.96 5 Silvan WICKI SUI 19.98 20.45 20.45 DLR 19.26 Yohan BLAKE JAM Boudewijnstadion, Bruxelles 16.09.11 6 Adam GEMILI GBR 19.94 19.97 20.56 SB 19.76 Noah LYLES USA Stade Louis II, Monaco 14.08.20 7 Bruno HORTELANO-ROIG ESP 20.04 20.04 8 Elijah HALL USA 19.32 20.11 20.69 2020 World Outdoor list 19.76 +0.7 Noah LYLES USA Stade Louis II, Monaco (MON) 14.08.20 19.80 +1.0 Kenneth BEDNAREK USA Montverde, FL (USA) 10.08.20 Medal Winners Stockholm previous 19.96 +1.0 Steven GARDINER BAH Clermont, FL (USA) 25.07.20 20.22 +0.8 Divine ODUDURU NGR Clermont, FL (USA) 25.07.20 2019 - IAAF World Ch. in Athletics Winners 20.23 +0.1 Clarence MUNYAI RSA Pretoria (RSA) 13.03.20 1. Noah LYLES (USA) 19.83 19 Aaron BROWN (CAN) 20.06 20.24 +0.8 André DE GRASSE CAN Clermont, FL (USA) 25.07.20 2. -
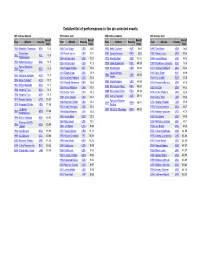
Detailed List of Performances in the Six Selected Events
Detailed list of performances in the six selected events 100 metres women 100 metres men 400 metres women 400 metres men Result Result Result Result Year Athlete Country Year Athlete Country Year Athlete Country Year Athlete Country (sec) (sec) (sec) (sec) 1928 Elizabeth Robinson USA 12.2 1896 Tom Burke USA 12.0 1964 Betty Cuthbert AUS 52.0 1896 Tom Burke USA 54.2 Stanislawa 1900 Frank Jarvis USA 11.0 1968 Colette Besson FRA 52.0 1900 Maxey Long USA 49.4 1932 POL 11.9 Walasiewicz 1904 Archie Hahn USA 11.0 1972 Monika Zehrt GDR 51.08 1904 Harry Hillman USA 49.2 1936 Helen Stephens USA 11.5 1906 Archie Hahn USA 11.2 1976 Irena Szewinska POL 49.29 1908 Wyndham Halswelle GBR 50.0 Fanny Blankers- 1908 Reggie Walker SAF 10.8 1980 Marita Koch GDR 48.88 1912 Charles Reidpath USA 48.2 1948 NED 11.9 Koen 1912 Ralph Craig USA 10.8 Valerie Brisco- 1920 Bevil Rudd SAF 49.6 1984 USA 48.83 1952 Marjorie Jackson AUS 11.5 Hooks 1920 Charles Paddock USA 10.8 1924 Eric Liddell GBR 47.6 1956 Betty Cuthbert AUS 11.5 1988 Olga Bryzgina URS 48.65 1924 Harold Abrahams GBR 10.6 1928 Raymond Barbuti USA 47.8 1960 Wilma Rudolph USA 11.0 1992 Marie-José Pérec FRA 48.83 1928 Percy Williams CAN 10.8 1932 Bill Carr USA 46.2 1964 Wyomia Tyus USA 11.4 1996 Marie-José Pérec FRA 48.25 1932 Eddie Tolan USA 10.3 1936 Archie Williams USA 46.5 1968 Wyomia Tyus USA 11.0 2000 Cathy Freeman AUS 49.11 1936 Jesse Owens USA 10.3 1948 Arthur Wint JAM 46.2 1972 Renate Stecher GDR 11.07 Tonique Williams- 1948 Harrison Dillard USA 10.3 1952 George Rhoden JAM 45.9 2004 BAH 49.41 1976 -
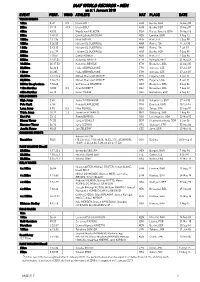
IAAF WORLD RECORDS - MEN As at 1 January 2018 EVENT PERF
IAAF WORLD RECORDS - MEN as at 1 January 2018 EVENT PERF. WIND ATHLETE NAT PLACE DATE TRACK EVENTS 100m 9.58 0.9 Usain BOLT JAM Berlin, GER 16 Aug 09 200m 19.19 -0.3 Usain BOLT JAM Berlin, GER 20 Aug 09 400m 43.03 Wayde van NIEKERK RSA Rio de Janeiro, BRA 14 Aug 16 800m 1:40.91 David Lekuta RUDISHA KEN London, GBR 9 Aug 12 1000m 2:11.96 Noah NGENY KEN Rieti, ITA 5 Sep 99 1500m 3:26.00 Hicham EL GUERROUJ MAR Roma, ITA 14 Jul 98 1 Mile 3:43.13 Hicham EL GUERROUJ MAR Roma, ITA 7 Jul 99 2000m 4:44.79 Hicham EL GUERROUJ MAR Berlin, GER 7 Sep 99 3000m 7:20.67 Daniel KOMEN KEN Rieti, ITA 1 Sep 96 5000m 12:37.35 Kenenisa BEKELE ETH Hengelo, NED 31 May 04 10,000m 26:17.53 Kenenisa BEKELE ETH Bruxelles, BEL 26 Aug 05 20,000m 56:26.0 Haile GEBRSELASSIE ETH Ostrava, CZE 27 Jun 07 1 Hour 21,285 Haile GEBRSELASSIE ETH Ostrava, CZE 27 Jun 07 25,000m 1:12:25.4 Moses Cheruiyot MOSOP KEN Eugene, USA 3 Jun 11 30,000m 1:26:47.4 Moses Cheruiyot MOSOP KEN Eugene, USA 3 Jun 11 3000m Steeplechase 7:53.63 Saif Saaeed SHAHEEN QAT Bruxelles, BEL 3 Sep 04 110m Hurdles 12.80 0.3 Aries MERRITT USA Bruxelles, BEL 7 Sep 12 400m Hurdles 46.78 Kevin YOUNG USA Barcelona, ESP 6 Aug 92 FIELD EVENTS High Jump 2.45 Javier SOTOMAYOR CUB Salamanca, ESP 27 Jul 93 Pole Vault 6.16i Renaud LAVILLENIE FRA Donetsk, UKR 15 Feb 14 Long Jump 8.95 0.3 Mike POWELL USA Tokyo, JPN 30 Aug 91 Triple Jump 18.29 1.3 Jonathan EDWARDS GBR Göteborg, SWE 7 Aug 95 Shot Put 23.12 Randy BARNES USA Los Angeles, USA 20 May 90 Discus Throw 74.08 Jürgen SCHULT GDR Neubrandenburg, GDR 6 Jun 86 Hammer Throw