Maxima and Minima in Plane Geometry
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Engineering Drawing (NSQF) - 1St Year Common for All Engineering Trades Under CTS (Not Applicable for Draughtsman Trade Group)
ENGINEERING DRAWING (NSQF) 1st Year Common for All Engineering Trades under CTS (Not applicable for Draughtsman Trade Group) (For all 1 Year & 2 Year Trades) DIRECTORATE GENERAL OF TRAINING MINISTRY OF SKILL DEVELOPMENT & ENTREPRENEURSHIP GOVERNMENT OF INDIA NATIONAL INSTRUCTIONAL MEDIA INSTITUTE, CHENNAI Post Box No. 3142, CTI Campus, Guindy, Chennai - 600 032 (i) Copyright Free. Under CC BY License. Engineering Drawing (NSQF) - 1st Year Common for all Engineering Trades under CTS (Not applicable for Draughtsman Trade Group) Developed & Published by National Instructional Media Institute Post Box No.3142 Guindy, Chennai - 32 INDIA Email: [email protected] Website: www.nimi.gov.in Printed by National Instructional Media Institute Chennai - 600 032 First Edition :November 2019 Rs.170/- © (ii) Copyright Free. Under CC BY License. FOREWORD The Government of India has set an ambitious target of imparting skills to 30 crores people, one out of every four Indians, by 2020 to help them secure jobs as part of the National Skills Development Policy. Industrial Training Institutes (ITIs) play a vital role in this process especially in terms of providing skilled manpower. Keeping this in mind, and for providing the current industry relevant skill training to Trainees, ITI syllabus has been recently updated with the help of comprising various stakeholder's viz. Industries, Entrepreneurs, Academicians and representatives from ITIs. The National Instructional Media Institute (NIMI), Chennai, has now come up with instructional material to suit the revised curriculum for Engineering Drawing 1st Year (For All 1 year & 2 year Trades) NSQF Commom for all engineering trades under CTS will help the trainees to get an international equivalency standard where their skill proficiency and competency will be duly recognized across the globe and this will also increase the scope of recognition of prior learning. -

Tessellation Techniques
Tessellation Techniques Stefanie Mandelbaum Jacqueline S. Guttman 118 Tunicflower Lane West Windsor, NJ 08550, USA E-mail [email protected] Abstract Tessellations are continuous repetitions of the same geometric or organic shape, a tile or tessera in Latin . Inspired by the abstract tessellations of the Alhambra, aided by a correspondence with Coxeter, Escher developed a method of transforming polygonal tessellations into representational tessellations of organic shapes. Mathematical Presentation Tessellations of polygons can be edge-to-edge and vertex-to-vertex (Fig. 1) or translated to be edge-to- edge but not vertex-to-vertex (Fig. 2). Figure 1: Quadrilaterals, edge-to-edge and vertex-to-vertex Figure 2: Quadrilaterals, translated Escher first determined which polygons could tessellate by themselves, e.g. triangles, quadrilaterals, regular hexagons (Figs. 3 and 4 ), and which could not, e.g. regular octagons and regular pentagons (Fig. 5). (A polygon is regular if all of its sides and interior angles are congruent.) Figure 3: Quadrilaterals Figure 4: Triangles Figure 5: Regular Pentagons At the vertex of a tessellation, the sum of the angles of the adjacent polygons is 360 degrees. So, for example, a regular hexagon can tessellate by itself because at the vertex of the tessellation the sum of the angles is 360 degrees, each of the three adjoining angles being 120 degrees (Fig. 6). Conversely, regular octagons cannot tessellate by themselves because each angle of a regular octagon is 135 degrees and 135 is not a factor of 360 (Fig. 7). 2(135)=270. 360-270=90. Therefore, the other polygon needed to complete the tessellation is a square. -

SOFTIMAGE|XSI Application Uses Jscript and Visual Basic Scripting Edition from Microsoft Corporation
SOFTIMAGE®|XSI® Version 4.0 Modeling & Deformations © 1999–2004 Avid Technology, Inc. All rights reserved. Avid, meta–clay, SOFTIMAGE, XSI, and the XSI logo are either registered trademarks or trademarks of Avid Technology, Inc. in the United States and/ or other countries. mental ray and mental images are registered trademarks of mental images GmbH & Co. KG in the U.S.A. and some other countries. mental ray Phenomenon, mental ray Phenomena, Phenomenon, Phenomena, Software Protection Manager, and SPM are trademarks or, in some countries, registered trademarks of mental images GmbH & Co. KG. All other trademarks contained herein are the property of their respective owners. This software includes the Python Release 2.3.2 software. The Python software is: Copyright © 2001, 2002, 2003 Python Software Foundation. All rights reserved. Copyright © 2000 BeOpen.com. All rights reserved. Copyright © 1995-2000 Corporation for National Research Initiatives. All rights reserved. Copyright © 1991-1995 Stichting Mathematisch Centrum. All rights reserved. The SOFTIMAGE|XSI application uses JScript and Visual Basic Scripting Edition from Microsoft Corporation. Activision is a registered trademark of Activision, Inc. © 1998 Activision, Inc. Battlezone is a trademark of and © 1998 Atari Interactive, Inc., a Hasbro company. All rights reserved. Licensed by Activision. This document is protected under copyright law. The contents of this document may not be copied or duplicated in any form, in whole or in part, without the express written permission of Avid Technology, Inc. This document is supplied as a guide for the Softimage product. Reasonable care has been taken in preparing the information it contains. However, this document may contain omissions, technical inaccuracies, or typographical errors. -

Fundamental Theorems in Mathematics
SOME FUNDAMENTAL THEOREMS IN MATHEMATICS OLIVER KNILL Abstract. An expository hitchhikers guide to some theorems in mathematics. Criteria for the current list of 243 theorems are whether the result can be formulated elegantly, whether it is beautiful or useful and whether it could serve as a guide [6] without leading to panic. The order is not a ranking but ordered along a time-line when things were writ- ten down. Since [556] stated “a mathematical theorem only becomes beautiful if presented as a crown jewel within a context" we try sometimes to give some context. Of course, any such list of theorems is a matter of personal preferences, taste and limitations. The num- ber of theorems is arbitrary, the initial obvious goal was 42 but that number got eventually surpassed as it is hard to stop, once started. As a compensation, there are 42 “tweetable" theorems with included proofs. More comments on the choice of the theorems is included in an epilogue. For literature on general mathematics, see [193, 189, 29, 235, 254, 619, 412, 138], for history [217, 625, 376, 73, 46, 208, 379, 365, 690, 113, 618, 79, 259, 341], for popular, beautiful or elegant things [12, 529, 201, 182, 17, 672, 673, 44, 204, 190, 245, 446, 616, 303, 201, 2, 127, 146, 128, 502, 261, 172]. For comprehensive overviews in large parts of math- ematics, [74, 165, 166, 51, 593] or predictions on developments [47]. For reflections about mathematics in general [145, 455, 45, 306, 439, 99, 561]. Encyclopedic source examples are [188, 705, 670, 102, 192, 152, 221, 191, 111, 635]. -

Geometryassessments Algebra II Assessments
Geometry}iLÀ>Ê AssessmentsÃÃiÃÃiÌÃ «iÀvÀ>ViÊÌ>ÃÃÊ>}i`ÊÌÊÌ iÊ/iÝ>ÃÊÃÌ>`>À`Ã The Charles A. Dana Center >ÌÊ/ iÊ1ÛiÀÃÌÞÊvÊ/iÝ>ÃÊ>ÌÊÕÃÌ ! PUBLICATION OF THE #HARLES ! $ANA #ENTER AN ORGANIZED RESEARCH UNIT OF 4HE 5NIVERSITY OF 4EXAS AT !USTIN About The University of Texas at Austin Charles A. Dana Center The Charles A. Dana Center supports education leaders and policymakers in strengthening education. As a research unit of The University of Texas at Austin’s College of Natural Sciences, the Dana Center maintains a special emphasis on mathematics and science education. The Dana Center’s mission is to strengthen the mathematics and science preparation and achievement of all students through supporting alignment of all the key components of mathematics and science education, prekindergarten–16: the state standards, accountability system, assessment, and teacher preparation. We focus our efforts on providing resources to help local communities meet the demands of the education system—by working with leaders, teachers, and students through our Instructional Support System; by strengthening mathematics and science professional development; and by publishing and disseminating mathematics and science education resources. About the development of this book The Charles A. Dana Center has developed this standards-aligned mathematics education resource for mathematics teachers. The development and production of the first edition of Geometry Assessments was supported by the National Science Foundation and the Charles A. Dana Center at the University of Texas at Austin. The development and production of this second edition was supported by the Charles A. Dana Center. Any opinions, findings, conclusions, or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation or The University of Texas at Austin. -

MYSTERIES of the EQUILATERAL TRIANGLE, First Published 2010
MYSTERIES OF THE EQUILATERAL TRIANGLE Brian J. McCartin Applied Mathematics Kettering University HIKARI LT D HIKARI LTD Hikari Ltd is a publisher of international scientific journals and books. www.m-hikari.com Brian J. McCartin, MYSTERIES OF THE EQUILATERAL TRIANGLE, First published 2010. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, without the prior permission of the publisher Hikari Ltd. ISBN 978-954-91999-5-6 Copyright c 2010 by Brian J. McCartin Typeset using LATEX. Mathematics Subject Classification: 00A08, 00A09, 00A69, 01A05, 01A70, 51M04, 97U40 Keywords: equilateral triangle, history of mathematics, mathematical bi- ography, recreational mathematics, mathematics competitions, applied math- ematics Published by Hikari Ltd Dedicated to our beloved Beta Katzenteufel for completing our equilateral triangle. Euclid and the Equilateral Triangle (Elements: Book I, Proposition 1) Preface v PREFACE Welcome to Mysteries of the Equilateral Triangle (MOTET), my collection of equilateral triangular arcana. While at first sight this might seem an id- iosyncratic choice of subject matter for such a detailed and elaborate study, a moment’s reflection reveals the worthiness of its selection. Human beings, “being as they be”, tend to take for granted some of their greatest discoveries (witness the wheel, fire, language, music,...). In Mathe- matics, the once flourishing topic of Triangle Geometry has turned fallow and fallen out of vogue (although Phil Davis offers us hope that it may be resusci- tated by The Computer [70]). A regrettable casualty of this general decline in prominence has been the Equilateral Triangle. Yet, the facts remain that Mathematics resides at the very core of human civilization, Geometry lies at the structural heart of Mathematics and the Equilateral Triangle provides one of the marble pillars of Geometry. -

1970-2020 TOPIC INDEX for the College Mathematics Journal (Including the Two Year College Mathematics Journal)
1970-2020 TOPIC INDEX for The College Mathematics Journal (including the Two Year College Mathematics Journal) prepared by Donald E. Hooley Emeriti Professor of Mathematics Bluffton University, Bluffton, Ohio Each item in this index is listed under the topics for which it might be used in the classroom or for enrichment after the topic has been presented. Within each topic entries are listed in chronological order of publication. Each entry is given in the form: Title, author, volume:issue, year, page range, [C or F], [other topic cross-listings] where C indicates a classroom capsule or short note and F indicates a Fallacies, Flaws and Flimflam note. If there is nothing in this position the entry refers to an article unless it is a book review. The topic headings in this index are numbered and grouped as follows: 0 Precalculus Mathematics (also see 9) 0.1 Arithmetic (also see 9.3) 0.2 Algebra 0.3 Synthetic geometry 0.4 Analytic geometry 0.5 Conic sections 0.6 Trigonometry (also see 5.3) 0.7 Elementary theory of equations 0.8 Business mathematics 0.9 Techniques of proof (including mathematical induction 0.10 Software for precalculus mathematics 1 Mathematics Education 1.1 Teaching techniques and research reports 1.2 Courses and programs 2 History of Mathematics 2.1 History of mathematics before 1400 2.2 History of mathematics after 1400 2.3 Interviews 3 Discrete Mathematics 3.1 Graph theory 3.2 Combinatorics 3.3 Other topics in discrete mathematics (also see 6.3) 3.4 Software for discrete mathematics 4 Linear Algebra 4.1 Matrices, systems -

Heid, M. Kathleen, Ed. Teaching and Learning Mathematics
DOCUMENT RESUME ED 423 111 SE 061 416 AUTHOR Blume, Glendon W., Ed.; Heid, M. Kathleen, Ed. TITLE Teaching and Learning Mathematics with Technology. 1997 Yearbook. INSTITUTION Pennsylvania Council of Teachers of Mathematics, University Park. PUB DATE 1997-00-00 NOTE 92p. AVAILABLE FROM Pennsylvania Council of Teachers of Mathematics, Pennsylvania State University, 270 Chambers Bldg., University Park, PA 16802. PUB TYPE Reports Descriptive (141) EDRS PRICE MF01/PC04 Plus Postage. DESCRIPTORS *Computer Uses in Education; *Educational Technology; Elementary Secondary Education; Fractions; Functions (Mathematics); Geometry; *Graphing Calculators; *Mathematics Education; Spreadsheets; Teaching Methods ABSTRACT This yearbook focuses on the role of technology in school mathematics. Chapters are replete with classroom-tested ideas for using technology to teach new mathematical ideas and to teach familiar mathematical ideas better. Chapters included: (1) "Using the Graphing Calculator in the Classroom: Helping Students Solve the "Unsolvable" (Eric Milou, Edward Gambler, Todd Moyer); (2) "Graphing Changing Awirages" (Davis Duncan, Bonnie Litwiller); (3) "Making More of an Average 1,2sscn: Using Sp).eadsheets To Teach Preservice Teachers about Average" (John Baker) ; (4) "In the Presence of Technology, Geometry is Alive and Well--but Different" (Gina Foletta); (5) "Composing Functions Graphically on the TI-92" (Linda Iseri); (6) "Signifiers and Counterparts: Building a Framework for Analyzing Students' Use of Symbols" (Margaret Kinzel); (7) "Exploring Continued Fractions: A Technological Approach" (Tom Evitts); (8) "The Isosceles Triangle: Making Connections with the TI-92" (Karen Flanagan, Ken Kerr); and (9) "Mathematically Modeling a Traffic Intersection" (Jon Wetherbee) . (ASK) ******************************************************************************** Reproductions supplied by EDRS are the best that can be made from the original document. -

TIMES and EQUIVALENT SYSTEMS II 6.1 for Concurrent
1 of 6 TIMES AND EQUIVALENT SYSTEMS II 6.1 for concurrent forces Varignon theorem: Varignon's theorem is a statement in Euclidean geometry by Pierre Varignon that was first published in 1731. It deals with the construction of a particular parallelogram (Varignon parallelogram) from an arbitrary quadrangle. The midpoints of the sides of an arbitrary quadrangle form a parallelogram. If the quadrangle is convex or reentrant, i.e. not a crossing quadrangle, then the area of the parallelogram is half as big as the area of the quadrangle. If one introduces the concept of oriented areas for n-gons, then the area equality above holds for crossed quadrangles as well. The Varignon parallelogram exists even for a skew quadrilateral, and is planar whether or not the quadrilateral is planar. It can be generalized to the midpoint polygon of an arbitrary polygon. Special cases The Varignon parallelogram is a rhombus if and only if the two diagonals of the quadrilateral have equal length, that is, if the quadrilateral is an equidiagonal quadrilateral. The Varignon parallelogram is a rectangle if and only if the diagonals of the quadrilateral are perpendicular, that is, if the quadrilateral is an orthodiagonal quadrilateral. Proof Varignon's theorem is easily proved as a theorem of affine geometry organized as linear algebra with the linear combinations restricted to coefficients summing to 1, also called affine orbarycentric coordinates. The proof applies even to skew quadrilaterals in spaces of any dimension. Any three points E, F, G are completed to a parallelogram (lying in the plane containing E, F, and G) by taking its fourth vertex to be E − F + G. -

JMM 2015 Student Poster Session Abstract Book
Abstracts for the MAA Undergraduate Poster Session San Antonio, TX January 12, 2015 Organized by Joyati Debnath Winona State University CELEBRATING A CENTURY OF ADVANCING MATHEMATICS Organized by the MAA Committee on Undergraduate Student Activities and Chapters and CUPM Subcommittee on Research by Undergraduates Dear Students, Advisors, Judges and Colleagues, If you look around today you will see about 273 posters and 492 presenters, record numbers, once again. It is so rewarding to see this session, which offers such a great opportunity for interaction between students and professional mathematicians, continue to grow. The judges you see here today are professional mathematicians from institutionsaround the world. They are advisors, colleagues, new PhD.s, and administrators. We have acknowledgedmany of them in this book- let; however, many judges here volunteered on site. Their support is vital to the success of the session and we thank them. We are supported financially by the National Science Foundation. Our online submission system and technical support is key to managing the ever-growing number of poster entries we receive. Thanks to MAA staff, especially Julia Dills and Maia Henley for their work setting up and managing the system this year. Preparation of the abstract book is a time-consuming task. Thanks to Beverly Ruedi for doing the final production work on the abstract book. There are many details of the poster session that begin with putting out the advertisement in FOCUS in February, ensuring students have travel money, and organizing tables in the room we are in today that are attributed to Gerard Venema (MAA Associate Secretary), Linda Braddy (MAA), and Donna Salter (AMS). -

Geometryassessments
Geometry Assessments The Charles A. Dana Center at The University of Texas at Austin With funding from the Texas Education Agency and the National Science Foundation 48810 Frontmatter 59 8/21/02, 11:19 AM 48810 Frontmatter 1 8/21/02, 11:19 AM About the Charles A. Dana Center’s Work in Mathematics and Science The Charles A. Dana Center at The University of Texas at Austin works to support education leaders and policymakers in strengthening Texas edu- cation. As a research unit of UT Austin’s College of Natural Sciences, the Dana Center maintains a special emphasis on mathematics and science education. We offer professional development institutes and produce research-based mathematics and science resources for educators to use in helping all students achieve academic success. For more information, visit the Dana Center website at www.utdanacenter.org. The development of this work is supported in part by the Texas Education Agency, the National Science Foundation under cooperative agreement #ESR-9712001, and the Charles A. Dana Center at The University of Texas at Austin. Any opinions, findings, conclusions, or recommendations expressed in this material are those of the author(s) and do not necessar- ily reflect the views of the Texas Education Agency, the National Science Foundation, or The University of Texas at Austin. Permission is given to any person, group, or organization to copy and distribute this publication, Geometry Assessments, for noncommercial educational purposes only, so long as the appropriate credit is given. This permission is granted by the Charles A. Dana Center, a unit of the College of Natural Sciences at The University of Texas at Austin. -
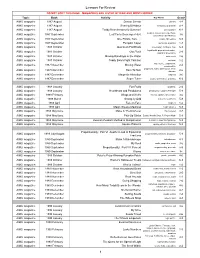
Lessons for Review
Lessons For Review DO NOT SORT THIS PAGE - MAGAZINES ARE LISTED IN YEAR AND MONTH ORDER Topic Book Activity Key Words Grade AIMS magazine 1987 August Densor Sensor density 4-8 AIMS magazine 1987 August Sharing Birthdays birthdays, probability 4-8 AIMS magazine 1987 August Teddy Bear dresses for Summer! permutations K-2 AIMS magazine 1987 September Leaf Facts Scavenger Hunt needles, leaves, scavenger hunt, 3-6 observation, identification AIMS magazine 1987 September One Potato, Two . potato, 3D regions 5-9 AIMS magazine 1987 September Pumpkin Caper pumpkins, graphing 1-3 AIMS magazine 1987 October Aluminum Foil Boats observation, foil boats, float 6-9 AIMS magazine 1987 October Goo Yuck liquid/solid, properties of matter, 2-8 graphing observation AIMS magazine 1987 October Moving Raindrops in the Water water cycle 2-6 AIMS magazine 1987 October Teddy Bears Fight Pollution pollution 1-2 AIMS magazine 1987 November Moving Water water cycle, evaporation, 2-4 condensation AIMS magazine 1987 November Rock 'N Rule properties, rocks, observation, Venn 2-6 diagram AIMS magazine 1987 December Magnetic Attraction magnets 3-6 AIMS magazine 1987 December Super Tuber potato, observation, graphing K-2 AIMS magazine 1988 January Fun Fruits graphing, 2-4 AIMS magazine 1988 January Heartbeats and Pendulums pendulums, Huggens Principle 5-9 AIMS magazine 1988 February Wings and Webs insects, spiders, observation 3-6 AIMS magazine 1988 March Strangely Odd sequences, patterns 5-9 AIMS magazine 1988 April Face to Face magnets 1-2 AIMS magazine 1988 April Magic