13 Functions and Expressions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Chapter 7 Expressions and Assignment Statements
Chapter 7 Expressions and Assignment Statements Chapter 7 Topics Introduction Arithmetic Expressions Overloaded Operators Type Conversions Relational and Boolean Expressions Short-Circuit Evaluation Assignment Statements Mixed-Mode Assignment Chapter 7 Expressions and Assignment Statements Introduction Expressions are the fundamental means of specifying computations in a programming language. To understand expression evaluation, need to be familiar with the orders of operator and operand evaluation. Essence of imperative languages is dominant role of assignment statements. Arithmetic Expressions Their evaluation was one of the motivations for the development of the first programming languages. Most of the characteristics of arithmetic expressions in programming languages were inherited from conventions that had evolved in math. Arithmetic expressions consist of operators, operands, parentheses, and function calls. The operators can be unary, or binary. C-based languages include a ternary operator, which has three operands (conditional expression). The purpose of an arithmetic expression is to specify an arithmetic computation. An implementation of such a computation must cause two actions: o Fetching the operands from memory o Executing the arithmetic operations on those operands. Design issues for arithmetic expressions: 1. What are the operator precedence rules? 2. What are the operator associativity rules? 3. What is the order of operand evaluation? 4. Are there restrictions on operand evaluation side effects? 5. Does the language allow user-defined operator overloading? 6. What mode mixing is allowed in expressions? Operator Evaluation Order 1. Precedence The operator precedence rules for expression evaluation define the order in which “adjacent” operators of different precedence levels are evaluated (“adjacent” means they are separated by at most one operand). -

A Concurrent PASCAL Compiler for Minicomputers
512 Appendix A DIFFERENCES BETWEEN UCSD'S PASCAL AND STANDARD PASCAL The PASCAL language used in this book contains most of the features described by K. Jensen and N. Wirth in PASCAL User Manual and Report, Springer Verlag, 1975. We refer to the PASCAL defined by Jensen and Wirth as "Standard" PASCAL, because of its widespread acceptance even though no international standard for the language has yet been established. The PASCAL used in this book has been implemented at University of California San Diego (UCSD) in a complete software system for use on a variety of small stand-alone microcomputers. This will be referred to as "UCSD PASCAL", which differs from the standard by a small number of omissions, a very small number of alterations, and several extensions. This appendix provides a very brief summary Of these differences. Only the PASCAL constructs used within this book will be mentioned herein. Documents are available from the author's group at UCSD describing UCSD PASCAL in detail. 1. CASE Statements Jensen & Wirth state that if there is no label equal to the value of the case statement selector, then the result of the case statement is undefined. UCSD PASCAL treats this situation by leaving the case statement normally with no action being taken. 2. Comments In UCSD PASCAL, a comment appears between the delimiting symbols "(*" and "*)". If the opening delimiter is followed immediately by a dollar sign, as in "(*$", then the remainder of the comment is treated as a directive to the compiler. The only compiler directive mentioned in this book is (*$G+*), which tells the compiler to allow the use of GOTO statements. -

Operators and Expressions
UNIT – 3 OPERATORS AND EXPRESSIONS Lesson Structure 3.0 Objectives 3.1 Introduction 3.2 Arithmetic Operators 3.3 Relational Operators 3.4 Logical Operators 3.5 Assignment Operators 3.6 Increment and Decrement Operators 3.7 Conditional Operator 3.8 Bitwise Operators 3.9 Special Operators 3.10 Arithmetic Expressions 3.11 Evaluation of Expressions 3.12 Precedence of Arithmetic Operators 3.13 Type Conversions in Expressions 3.14 Operator Precedence and Associability 3.15 Mathematical Functions 3.16 Summary 3.17 Questions 3.18 Suggested Readings 3.0 Objectives After going through this unit you will be able to: Define and use different types of operators in Java programming Understand how to evaluate expressions? Understand the operator precedence and type conversion And write mathematical functions. 3.1 Introduction Java supports a rich set of operators. We have already used several of them, such as =, +, –, and *. An operator is a symbol that tells the computer to perform certain mathematical or logical manipulations. Operators are used in programs to manipulate data and variables. They usually form a part of mathematical or logical expressions. Java operators can be classified into a number of related categories as below: 1. Arithmetic operators 2. Relational operators 1 3. Logical operators 4. Assignment operators 5. Increment and decrement operators 6. Conditional operators 7. Bitwise operators 8. Special operators 3.2 Arithmetic Operators Arithmetic operators are used to construct mathematical expressions as in algebra. Java provides all the basic arithmetic operators. They are listed in Tabled 3.1. The operators +, –, *, and / all works the same way as they do in other languages. -
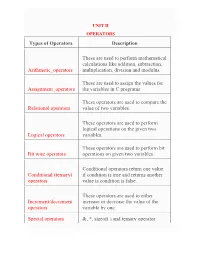
Types of Operators Description Arithmetic Operators These Are
UNIT II OPERATORS Types of Operators Description These are used to perform mathematical calculations like addition, subtraction, Arithmetic_operators multiplication, division and modulus These are used to assign the values for Assignment_operators the variables in C programs. These operators are used to compare the Relational operators value of two variables. These operators are used to perform logical operations on the given two Logical operators variables. These operators are used to perform bit Bit wise operators operations on given two variables. Conditional operators return one value Conditional (ternary) if condition is true and returns another operators value is condition is false. These operators are used to either Increment/decrement increase or decrease the value of the operators variable by one. Special operators &, *, sizeof( ) and ternary operator ARITHMETIC OPERATORS IN C: C Arithmetic operators are used to perform mathematical calculations like addition, subtraction, multiplication, division and modulus in C programs. Arithmetic Operators/Operation Example + (Addition) A+B – (Subtraction) A-B * (multiplication) A*B / (Division) A/B % (Modulus) A%B EXAMPLE PROGRAM FOR C ARITHMETIC OPERATORS: // Working of arithmetic operators #include <stdio.h> int main() { int a = 9,b = 4, c; c = a+b; printf("a+b = %d \n",c); c = a-b; printf("a-b = %d \n",c); c = a*b; printf("a*b = %d \n",c); c = a/b; printf("a/b = %d \n",c); c = a%b; printf("Remainder when a divided by b = %d \n",c); return 0; } Output a+b = 13 a-b = 5 a*b = 36 a/b = 2 Remainder when a divided by b=1 Assignment Operators The Assignment Operator evaluates an expression on the right of the expression and substitutes it to the value or variable on the left of the expression. -

Brief Overview of Python Programming Language
Brief Overview Chapter of Python 3 In this chapter » Introduction to Python » Python Keywords “Don't you hate code that's not properly » Identifiers indented? Making it [indenting] part of » Variables the syntax guarantees that all code is » Data Types properly indented.” » Operators » Expressions — G. van Rossum » Input and Output » Debugging » Functions » if..else Statements » 3.1 INTRODUCTION TO PYTHON for Loop » Nested Loops An ordered set of instructions or commands to be executed by a computer is called a program. The language used to specify those set of instructions to the computer is called a programming language for example Python, C, C++, Java, etc. This chapter gives a brief overview of Python programming language. Python is a very popular and easy to learn programming language, created by Guido van Rossum in 1991. It is used in a variety of fields, including software development, web development, scientific computing, big data 2021-22 Chap 3.indd 31 19-Jul-19 3:16:31 PM 32 INFORMATICS PRACTICES – CLASS XI and Artificial Intelligence. The programs given in this book are written using Python 3.7.0. However, one can install any version of Python 3 to follow the programs given. Download Python 3.1.1 Working with Python The latest version of To write and run (execute) a Python program, we need Python is available on the to have a Python interpreter installed on our computer official website: or we can use any online Python interpreter. The https://www.python. interpreter is also called Python shell. A sample screen org/ of Python interpreter is shown in Figure 3.1. -

Syntax of Mini-Pascal (Spring 2016)
Syntax of Mini-Pascal (Spring 2016) Mini-Pascal is a simplified (and slightly modified) subset of Pascal. Generally, the meaning of the features of Mini-Pascal programs are similar to their semantics in other common imperative languages, such as C. 1. Mini-Pascal allows nested functions and procedures, i.e. subroutines which are defined within another. A nested function is invisible outside of its immediately enclosing function (procedure / block), but can access preceding visible local objects (data, functions, etc.) of its enclosing functions (procedures / blocks). Within the same scope (procedure / function / block), identifiers must be unique but it is OK to redefine a name in an inner scope. 2. A var parameter is passed by reference , i.e. its address is passed, and inside the subroutine the parameter name acts as a synonym for the variable given as an argument. A called procedure or function can freely read and write a variable that the caller passed in the argument list. 3. Mini-Pascal includes a C-style assert statement (if an assertion fails the system prints out a diagnostic message and halts execution). 4. The Mini-Pascal operation a.size only applies to values of type array of T (where T is a type). There are only one-dimensional arrays. Array types are compatible only if they have the same element type. Arrays' indices begin with zero. The compatibility of array indices and array sizes is usually checked at run time. 5. By default, variables in Pascal are not initialized (with zero or otherwise); so they may initially contain rubbish values. -

What Is Python ?
Class-XI Computer Science Python Fundamentals Notes What is python ? Python is object oriented high level computer language developed by Guido Van Rossum in 1990s . It was named after a British TV show namely ‘Monty Python’s Flying circus’. Python is a programming language, as are C, Fortran, BASIC, PHP, etc. Some specific features of Python are as follows: • an interpreted (as opposed to compiled) language. Contrary to e.g. C or Fortran, one does not compile Python code before executing it. In addition, Python can be used interactively: many Python interpreters are available, from which commands and scripts can be executed. • a free software released under an open-source license: Python can be used and distributed free of charge, even for building commercial software. • multi-platform: Python is available for all major operating systems, Windows, Linux/Unix, MacOS X, most likely your mobile phone OS, etc. • a very readable language with clear non-verbose syntax • a language for which a large variety of high-quality packages are available for various applications, from web frameworks to scientific computing. • a language very easy to interface with other languages, in particular C and C++. • Some other features of the language are illustrated just below. For example, Python is an object-oriented language, with dynamic typing (the same variable can contain objects of different types during the course of a program). Python character set: • Letters : A-Z , a-z • Digits : 0-9 • Special symbols : space,+,-,*,/,** etc. • Whitespace : blank space, tabs(->),carriage return, newline, formfeed • Other characters :python can process all ASCII and unicode characters as part of data PYTHON TERMINOLOGY : Tokens: A smallest individual unit in a program is known as tokens. -

Software II: Principles of Programming Languages Why Expressions?
Software II: Principles of Programming Languages Lecture 7 – Expressions and Assignment Statements Why Expressions? • Expressions are the fundamental means of specifying computations in a programming language • To understand expression evaluation, need to be familiar with the orders of operator and operand evaluation • Essence of imperative languages is dominant role of assignment statements 1 Arithmetic Expressions • Arithmetic evaluation was one of the motivations for the development of the first programming languages • Arithmetic expressions consist of operators, operands, parentheses, and function calls Arithmetic Expressions: Design Issues • Design issues for arithmetic expressions – Operator precedence rules? – Operator associativity rules? – Order of operand evaluation? – Operand evaluation side effects? – Operator overloading? – Type mixing in expressions? 2 Arithmetic Expressions: Operators • A unary operator has one operand • A binary operator has two operands • A ternary operator has three operands Arithmetic Expressions: Operator Precedence Rules • The operator precedence rules for expression evaluation define the order in which “adjacent” operators of different precedence levels are evaluated • Typical precedence levels – parentheses – unary operators – ** (if the language supports it) – *, / – +, - 3 Arithmetic Expressions: Operator Associativity Rule • The operator associativity rules for expression evaluation define the order in which adjacent operators with the same precedence level are evaluated • Typical associativity -

Introduction to C++
Introduction to C++ CLASS- 4 Expressions, OOPS Concepts Anshuman Dixit Expressions C++ contains expressions, which can consist of one or more operands, zero or more operators to compute a value. Every expression produces some value which is assigned to the variable with the help of an assignment operator. Ex- (a+b) - c 4a2 - 5b +c (a+b) * (x+y) Anshuman Dixit Expressions An expression can be of following types: • Constant expressions • Integral expressions • Float expressions • Pointer expressions • Relational expressions • Logical expressions • Bitwise expressions • Special assignment expressions Anshuman Dixit Constant expressions A constant expression is an expression that consists of only constant values. It is an expression whose value is determined at the compile-time but evaluated at the run-time. It can be composed of integer, character, floating-point, and enumeration constants. Ex- Expression containing constant Constant value x = (2/3) * 4 (2/3) * 4 extern int y = 67 67 int z = 43 43 Anshuman Dixit Integral and Float Expressions An integer expression is an expression that produces the integer value as output after performing all the explicit and implicit conversions. Ex- (x * y) -5 (where x and y are integers) Float Expressions: A float expression is an expression that produces floating-point value as output after performing all the explicit and implicit conversions. Anshuman Dixit Pointer and relationship Expressions A pointer expression is an expression that produces address value as an output. Ex- &x, ptr, ptr++, ptr-- Relational Expressions- A relational expression is an expression that produces a value of type bool, which can be either true or false. -

Evaluation of Relational Operators and Query Optimization Kathleen Durant Phd CS 3200
Evaluation of relational operators and query optimization Kathleen Durant PhD CS 3200 1 Introduction • In network and hierarchical DBMSs, low-level procedural query language is generally embedded in high-level programming language. • Programmer’s responsibility to select most appropriate execution strategy. • With declarative languages such as SQL, user specifies what data is required rather than how it is to be retrieved. • Relieves user of knowing what constitutes good execution strategy. Pearson Education © 2014 2 Introduction • Also gives DBMS more control over system performance. • Two main techniques for query optimization: • heuristic rules that order operations in a query; • comparing different strategies based on relative costs, and selecting one that minimizes resource usage. • Disk access tends to be dominant cost in query processing for centralized DBMS. Pearson Education © 2014 3 Query Processing Activities involved in retrieving data from the database. • Aims of QP: • transform query written in high-level language (e.g. SQL), into correct and efficient execution strategy expressed in low-level language (implementing RA); • execute strategy to retrieve required data. Pearson Education © 2014 4 Why is it important? • Now that we know about the benefits of indexes, how does the DBMS know when to use them? • An SQL query can be implemented in many ways, but which one is best? • Perform selection before or after join etc. • Many ways of physically implementing a join (or other relational operator), how to choose the right one? • The DBMS does this automatically, but we need to understand it to know what performance to expect 5 Query Evaluation • SQL query is implemented by a query plan • Tree of relational operators • Each internal node operates on its children • Can choose different operator implementations • Two main issues in query optimization: • For a given query, what plans are considered? • Algorithm to search plan space for cheapest (estimated) plan. -

Fortran 90 Standard Statement Keywords
APPENDIX A FORTRAN 90 STANDARD STATEMENT KEYWORDS For a given dialect of Fortran, there is normally some sort of refer ence document that formally specifies the valid syntax for each variety of statement. For most categories of statements, the syntax rules dic tate the appearance of fixed sequences of letters, traditionally known as keywords, at specified places in the statement. In particular, most state ments are required to begin with a keyword made up of a sequence of letters that constitute an ordinary word in the English language. Exam ples of such words are DO, END, and INTEGER. Some statements begin with a pair of keywords (for example, GO TO, DOUBLE PRECISION, ELSE IF). Furthermore, the term "keyword" encompasses certain sequences of letters appearing to the left of an equal sign (=) in a parenthesized list in certain (mostly I/O) statements. Consider, for example, the following statement: READ (UNIT = 15, FMT = "(A)", lOSTAT = ios) buf Here, the initial sequence of letters READ is, of course, a keyword, but also UNIT, FMT, and 10STAT are considered to be keywords, even though FMT and 10STAT are not English words. And, there are additional situ ations in Fortran where a particular sequence of letters appearing in a particular context is characterized as being a keyword. In Fortran 90, the sort of sequence of letters that has traditionally been called a "keyword" has been redesignated as a statement key word. The modifier "statement" has been prepended to distinguish the traditional sort of keyword from the Fortran 90 "argument keyword" as described in Section 13.9. -

Boolean Data and Relational Operators
BOOLEAN DATA AND RELATIONAL OPERATORS George Boole (1815-1864) was a British mathematician who invented the Boolean algebra, which is the basis of computer arithmetic for all modern computers. Because of this, we now consider Boole one of the founders of computer science even though electronic computers did not exist when he was alive. Boolean algebra involves “arithmetic” similar to that of numbers that you learned in school, except that a Boolean operation is either true or false. Java represents these two truth values using the keywords true and false, respectively. A variable of the built-in data type boolean can hold either the value true or false stored as an 8-bit integer. Example boolean done = false; boolean success = true; A relational operator takes two non-Boolean primitive operands, compares them and yields true or false. Relational Operators Symbol Operation Precedence Association < Less than <= Less than or equal to 6 Cannot be cascaded > Greater than >= Greater than or equal to See the topic Data Types and Operators → Introduction to Java Data Types and Operators Boolean Data and Relational Operators Page 1 Examples Assume x is initialized to 12.5. x < 12.0 is false x > 12.0 is true x <= 12.5 is true x <= 12.0 is false x >= 12.5 is true x >= 12.0 is true A relational operator is evaluated after all arithmetic operators and before any assignment operator. Example The follow statement determines if a student got 75% or better on a test boolean passedTest = (total-numberWrong) / total >= 0.75; Relational operators cannot be cascaded.