DOCSLIB.ORG

SAT Subject Physics Formula Reference Kinematics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
SAT Subject Physics Formula Reference Kinematics SAT Subject Physics Formula Reference This guide is a compilation of about fifty of the most importantphysicsformulastoknow for the SAT Subject test in physics. (Note that formulas are not given on the test.) Each formula row contains a description of the variables or constants that make up the formula, along with a brief explanation of the formula. Kinematics vave =averagevelocity ∆x The definition of average ve- vave = ∆x =displacement ∆t locity. ∆t =elapsedtime vave =averagevelocity (v + v ) Another definition of the av- v = i f ave 2 vi =initialvelocity erage velocity, which works a vf =finalvelocity when is constant. a =acceleration ∆v a = ∆t ∆v =changeinvelocity The definition of acceleration. ∆t =elapsedtime ∆x =displacement v 1 2 i =initialvelocity Use this formula when you ∆x = vi∆t + a(∆t) 2 ∆t =elapsedtime don’t have vf . a =acceleration ∆x =displacement vf =finalvelocity 1 2 Use this formula when you ∆x = vf ∆t − a(∆t) 2 ∆t =elapsedtime don’t have vi. a =acceleration www.erikthered.com/tutor pg. 1 SAT Subject Physics Formula Reference Kinematics (continued) vf =finalvelocity 2 2 vi =initialvelocity Use this formula when you vf = vi +2a∆x a =acceleration don’t have ∆t. ∆x =displacement Dynamics F =force Newton’s Second Law. Here, F = ma m =mass F is the net force on the mass a =acceleration m. W =weight The weight of an object with m W = mg =mass mass m.Thisisreallyjust g =accelerationdue Newton’s Second Law again. to gravity f =frictionforce The “Physics is Fun” equa- tion. Here, µ can be either µ =coefficient f = µN the kinetic coefficient of fric- of friction tion µ or the static coefficient N =normalforce k of friction µs. p =momentum The definition of momentum. p = mv m =mass It is conserved (constant) if there are no external forces on v =velocity asystem. www.erikthered.com/tutor pg. 2 SAT Subject Physics Formula Reference Dynamics (continued) ∆p =change in momentum ∆p = F ∆t F ∆t is called the impulse. F =appliedforce ∆t =elapsedtime Work, Energy, and Power W =work F =force W = Fdcos θ Work is done when a force d =distance is applied to an object as it or moves a distance d. F is the θ =anglebetweenF ! component of F in the direc- W = F!d and the direction tion that the object is moved. of motion F! =parallelforce KE = kinetic energy 1 The definition of kinetic en- KE = mv2 2 m =mass ergy for a mass m with veloc- v =velocity ity v. PE = potential energy m =mass The potential energy for a PE = mgh g =accelerationdue mass m at a height h above to gravity some reference level. h =height www.erikthered.com/tutor pg. 3 SAT Subject Physics Formula Reference Work, Energy, Power (continued) The “work-energy” theorem: W W =∆(KE) =workdone the work done by the net force KE = kinetic energy on an object equals the change in kinetic energy of the object. E=totalenergy The definition of total (“me- chanical”) energy. If there E=KE+PE KE = kinetic energy is no friction, it is conserved PE = potential energy (stays constant). P =power Power is the amount of work W P = W =work done per unit time (i.e., power ∆t is the rate at which work is ∆t =elapsedtime done). Circular Motion The “centripetal” acceleration 2 ac =centripetalacceleration v for an object moving around ac = v =velocity r in a circle of radius r at veloc- r =radius ity v. Fc =centripetalforce The “centripetal” force that is 2 mv m =mass needed to keep an object of Fc = r v =velocity mass m moving around in a circle of radius r at velocity v. r =radius www.erikthered.com/tutor pg. 4 SAT Subject Physics Formula Reference Circular Motion (continued) v =velocity This formula gives the veloc- 2πr v = r =radius ity v of an object moving once T around a circle of radius r in T =period time T (the period). 1 f =frequency The frequency is the number f = of times per second that an T T =period object moves around a circle. Torques and Angular Momentum τ =torque τ = rF sin θ r =distance(radius) Torque is a force applied at a distance r from the axis of ro- or F =force tation. F⊥ = F sin θ is the θ F τ = rF⊥ =anglebetween component of F perpendicu- and the lever arm lar to the lever arm. F⊥ =perpendicularforce L =angularmomentum Angular momentum is con- m =mass served (i.e., it stays constant) L = mvr v =velocity as long as there are no exter- nal torques. r =radius www.erikthered.com/tutor pg. 5 SAT Subject Physics Formula Reference Springs Fs =springforce “Hooke’s Law”. The force is k =springconstant Fs = kx opposite to the stretch or com- x =springstretchor pression direction. compression The potential energy stored PEs =potentialenergy in a spring when it is ei- k =springconstant 1 2 ther stretched or compressed. PEs = kx 2 x =amountof Here, x =0correspondsto spring stretch the “natural length” of the or compression spring. Gravity Fg =forceofgravity Newton’s Law of Gravitation: G =aconstant m1m2 this formula gives the attrac- Fg = G 2 r m1,m2 =masses tive force between two masses r =distanceof adistancer apart. separation Electric Fields and Forces Fe =electricforce “Coulomb’s Law”. This for- k =aconstant q1q2 mula gives the force of attrac- Fe = k 2 r q1,q2 =charges tion or repulsion between two r =distanceof charges a distance r apart. separation www.erikthered.com/tutor pg. 6 SAT Subject Physics Formula Reference Electric Fields and Forces (continued) Achargeq,whenplacedinan F =electricforce electric field E,willfeelaforce F = qE E =electricfield on it, given by this formula (q is sometimes called a “test” q =charge charge, since it tests the elec- tric field strength). E =electricfield This formula gives the elec- k =aconstant tric field due to a charge q at q adistancer from the charge. E = k 2 q =charge r Unlike the “test” charge, the r =distanceof charge q here is actually gen- separation erating the electric field. Between two large plates of metal separated by a distance E =electricfield V d which are connected to a E = V =voltage d battery of voltage V ,auni- d =distance form electric field between the plates is set up, as given by this formula. The potential difference ∆V ∆V =potentialdifference between two points (say, the W terminals of a battery), is de- ∆V = W =work q fined as the work per unit q =charge charge needed to move charge q from one point to the other. Circuits “Ohm’s Law”. This law gives V =voltage the relationship between the V = IR I =current battery voltage V ,thecurrent R =resistance I,andtheresistanceR in a circuit. www.erikthered.com/tutor pg. 7 SAT Subject Physics Formula Reference Circuits (continued) P = IV P =power All of these power formulas or are equivalent and give the 2 I =current P = V /R power used in a circuit resistor V =voltage or R.Usetheformulathathas R =resistance the quantities that you know. P = I2R Rs =total(series) When resistors are placed end resistance to end, which is called “in se- Rs = R1 =firstresistor ries”, the effective total resis- R1 + R2 + ... R2 =secondresistor tance is just the sum of the in- ... dividual resistances. When resistors are placed side 1 Rp =total(parallel) = resistance by side (or “in parallel”), the Rp effective total resistance is the R1 =firstresistor inverse of the sum of the re- 1 1 R2 =secondresistor + + ... ciprocals of the individual re- R1 R2 ... sistances (whew!). This formula is “Ohm’s Law” for capacitors. Here, C is a q =charge number specific to the capac- q = CV C =capacitance itor (like R for resistors), q is V =voltage the charge on one side of the capacitor, and V is the volt- age across the capacitor. www.erikthered.com/tutor pg. 8 SAT Subject Physics Formula Reference Magnetic Fields and Forces This formula gives the force F =forceonawire on a wire carrying current I I =currentinthewire while immersed in a magnetic L =lengthofwire field B.Here,θ is the angle F = ILB sin θ between the direction of the B =externalmagneticfield current and the direction of θ =anglebetweenthe the magnetic field (θ is usu- current direction and ally 90◦,sothattheforceis the magnetic field F = ILB). The force on a charge q as it F =forceonacharge travels with velocity v through q =charge amagneticfieldB is given by v =velocityofthecharge this formula. Here, θ is the F = qvB sin θ angle between the direction of B =externalmagneticfield the charge’s velocity and the θ =anglebetweenthe direction of the magnetic field direction of motion and (θ is usually 90◦,sothatthe the magnetic field force is F = qvB). Waves and Optics This formula relates the wave- v =wavevelocity length and the frequency of a v = λf λ =wavelength wave to its speed. The for- f =frequency mula works for both sound and light waves. When light travels through a v =velocityoflight medium (say, glass), it slows c down. This formula gives the v = c =vacuumlightspeed n speed of light in a medium n =indexofrefraction that has an index of refraction n.Here,c =3.0 × 108 m/s. www.erikthered.com/tutor pg. 9 SAT Subject Physics Formula Reference Waves and Optics (continued) “Snell’s Law”. When light moves from one medium (say, n1 =incidentindex air) to another (say, glass) θ1 =incidentangle with a different index of re- n1 sin θ1 = n2 sin θ2 n2 =refractedindex fraction n,itchangesdirec- tion (refracts). The angles are θ2 =refractedangle taken from the normal (per- pendicular).
Load more

Recommended publications
  • At—At, Batch—Execute Commands at a Later Time
    at—at, batch—execute commands at a later time at [–csm] [–f script] [–qqueue] time [date] [+ increment] at –l [ job...] at –r job... batch at and batch read commands from standard input to be executed at a later time. at allows you to specify when the commands should be executed, while jobs queued with batch will execute when system load level permits. Executes commands read from stdin or a file at some later time. Unless redirected, the output is mailed to the user. Example A.1 1 at 6:30am Dec 12 < program 2 at noon tomorrow < program 3 at 1945 pm August 9 < program 4 at now + 3 hours < program 5 at 8:30am Jan 4 < program 6 at -r 83883555320.a EXPLANATION 1. At 6:30 in the morning on December 12th, start the job. 2. At noon tomorrow start the job. 3. At 7:45 in the evening on August 9th, start the job. 4. In three hours start the job. 5. At 8:30 in the morning of January 4th, start the job. 6. Removes previously scheduled job 83883555320.a. awk—pattern scanning and processing language awk [ –fprogram–file ] [ –Fc ] [ prog ] [ parameters ] [ filename...] awk scans each input filename for lines that match any of a set of patterns specified in prog. Example A.2 1 awk '{print $1, $2}' file 2 awk '/John/{print $3, $4}' file 3 awk -F: '{print $3}' /etc/passwd 4 date | awk '{print $6}' EXPLANATION 1. Prints the first two fields of file where fields are separated by whitespace. 2. Prints fields 3 and 4 if the pattern John is found.
    [Show full text]
  • Glossary Physics (I-Introduction)
    1 Glossary Physics (I-introduction) - Efficiency: The percent of the work put into a machine that is converted into useful work output; = work done / energy used [-]. = eta In machines: The work output of any machine cannot exceed the work input (<=100%); in an ideal machine, where no energy is transformed into heat: work(input) = work(output), =100%. Energy: The property of a system that enables it to do work. Conservation o. E.: Energy cannot be created or destroyed; it may be transformed from one form into another, but the total amount of energy never changes. Equilibrium: The state of an object when not acted upon by a net force or net torque; an object in equilibrium may be at rest or moving at uniform velocity - not accelerating. Mechanical E.: The state of an object or system of objects for which any impressed forces cancels to zero and no acceleration occurs. Dynamic E.: Object is moving without experiencing acceleration. Static E.: Object is at rest.F Force: The influence that can cause an object to be accelerated or retarded; is always in the direction of the net force, hence a vector quantity; the four elementary forces are: Electromagnetic F.: Is an attraction or repulsion G, gravit. const.6.672E-11[Nm2/kg2] between electric charges: d, distance [m] 2 2 2 2 F = 1/(40) (q1q2/d ) [(CC/m )(Nm /C )] = [N] m,M, mass [kg] Gravitational F.: Is a mutual attraction between all masses: q, charge [As] [C] 2 2 2 2 F = GmM/d [Nm /kg kg 1/m ] = [N] 0, dielectric constant Strong F.: (nuclear force) Acts within the nuclei of atoms: 8.854E-12 [C2/Nm2] [F/m] 2 2 2 2 2 F = 1/(40) (e /d ) [(CC/m )(Nm /C )] = [N] , 3.14 [-] Weak F.: Manifests itself in special reactions among elementary e, 1.60210 E-19 [As] [C] particles, such as the reaction that occur in radioactive decay.
    [Show full text]
  • The Experimental Determination of the Moment of Inertia of a Model Airplane Michael Koken [email protected]
    The University of Akron IdeaExchange@UAkron The Dr. Gary B. and Pamela S. Williams Honors Honors Research Projects College Fall 2017 The Experimental Determination of the Moment of Inertia of a Model Airplane Michael Koken [email protected] Please take a moment to share how this work helps you through this survey. Your feedback will be important as we plan further development of our repository. Follow this and additional works at: http://ideaexchange.uakron.edu/honors_research_projects Part of the Aerospace Engineering Commons, Aviation Commons, Civil and Environmental Engineering Commons, Mechanical Engineering Commons, and the Physics Commons Recommended Citation Koken, Michael, "The Experimental Determination of the Moment of Inertia of a Model Airplane" (2017). Honors Research Projects. 585. http://ideaexchange.uakron.edu/honors_research_projects/585 This Honors Research Project is brought to you for free and open access by The Dr. Gary B. and Pamela S. Williams Honors College at IdeaExchange@UAkron, the institutional repository of The nivU ersity of Akron in Akron, Ohio, USA. It has been accepted for inclusion in Honors Research Projects by an authorized administrator of IdeaExchange@UAkron. For more information, please contact [email protected], [email protected]. 2017 THE EXPERIMENTAL DETERMINATION OF A MODEL AIRPLANE KOKEN, MICHAEL THE UNIVERSITY OF AKRON Honors Project TABLE OF CONTENTS List of Tables ................................................................................................................................................
    [Show full text]
  • TDS) EDEN PG MV® Pigment Ink for Textile
    Technical Data Sheet (TDS) EDEN PG MV® Pigment Ink for Textile Product Description: Applications: EDEN PG MV water based pigment Ink is ideal for high-speed direct digital printing on all standard fabrics available on the market. The ink prints on all types of fabrics with equal quality and coverage without color shifts or patches. EDEN PG MV Pigment Ink may be used on cotton, cotton blends, polyester, polyamide (nylon) and treated & untreated fabrics. EDEN PG MV is ideal for a wide range of applications including sportswear, footwear, fashion, home décor and home textile and is designed for indoor and outdoor applications. This ink is manufactured using cutting edge technology and • Home textile • Bags • Indoor furnishing high-performance pigments, for optimal ink fluidity and • Décor • Sport apparel • Fashion & apparel printability through piezo printheads without bleeding or • Footwear migration. Compatible Print Head Technology: Ricoh Gen 4 & Gen 5 Industrial print heads based printers. Pre-treatment: The use of Bordeaux EDEN PG™ OS® (pretreatment liquid) is Product Line: recommended in order to achieve higher chemical attributes (see table below for comparison). The pretreatment process for fabrics is done offline using a standard textile padder. Red Cleaning Print procedure: Cyan Magenta Yellow Black Magenta Liquid The printing process can be done either inline or in individual segments. Inline printing allows the printed fabric to be fed Material Compatibility: through a standard textile dryer directly. Alternatively, if the printing stage is separated from the drying stage, drying is • Cotton required before rolling the fabric. • Viscose • Polyester • Lycra Drying Working Parameters: • Silk Recommended drying time: 3 minutes • Polyamide Recommended temperature: 150°C (302°F) • Leather • Synthetic leather Post-treatment: No chemical post treatment is needed.
    [Show full text]
  • Motion Projectile Motion,And Straight Linemotion, Differences Between the Similaritiesand 2 CHAPTER 2 Acceleration Make Thefollowing As Youreadthe ●
    026_039_Ch02_RE_896315.qxd 3/23/10 5:08 PM Page 36 User-040 113:GO00492:GPS_Reading_Essentials_SE%0:XXXXXXXXXXXXX_SE:Application_File chapter 2 Motion section ●3 Acceleration What You’ll Learn Before You Read ■ how acceleration, time, and velocity are related Describe what happens to the speed of a bicycle as it goes ■ the different ways an uphill and downhill. object can accelerate ■ how to calculate acceleration ■ the similarities and differences between straight line motion, projectile motion, and circular motion Read to Learn Study Coach Outlining As you read the Velocity and Acceleration section, make an outline of the important information in A car sitting at a stoplight is not moving. When the light each paragraph. turns green, the driver presses the gas pedal and the car starts moving. The car moves faster and faster. Speed is the rate of change of position. Acceleration is the rate of change of velocity. When the velocity of an object changes, the object is accelerating. Remember that velocity is a measure that includes both speed and direction. Because of this, a change in velocity can be either a change in how fast something is moving or a change in the direction it is moving. Acceleration means that an object changes it speed, its direction, or both. How are speeding up and slowing down described? ●D Construct a Venn When you think of something accelerating, you probably Diagram Make the following trifold Foldable to compare and think of it as speeding up. But an object that is slowing down contrast the characteristics of is also accelerating. Remember that acceleration is a change in acceleration, speed, and velocity.
    [Show full text]
  • Frames of Reference
    Galilean Relativity 1 m/s 3 m/s Q. What is the women velocity? A. With respect to whom? Frames of Reference: A frame of reference is a set of coordinates (for example x, y & z axes) with respect to whom any physical quantity can be determined. Inertial Frames of Reference: - The inertia of a body is the resistance of changing its state of motion. - Uniformly moving reference frames (e.g. those considered at 'rest' or moving with constant velocity in a straight line) are called inertial reference frames. - Special relativity deals only with physics viewed from inertial reference frames. - If we can neglect the effect of the earth’s rotations, a frame of reference fixed in the earth is an inertial reference frame. Galilean Coordinate Transformations: For simplicity: - Let coordinates in both references equal at (t = 0 ). - Use Cartesian coordinate systems. t1 = t2 = 0 t1 = t2 At ( t1 = t2 ) Galilean Coordinate Transformations are: x2= x 1 − vt 1 x1= x 2+ vt 2 or y2= y 1 y1= y 2 z2= z 1 z1= z 2 Recall v is constant, differentiation of above equations gives Galilean velocity Transformations: dx dx dx dx 2 =1 − v 1 =2 − v dt 2 dt 1 dt 1 dt 2 dy dy dy dy 2 = 1 1 = 2 dt dt dt dt 2 1 1 2 dz dz dz dz 2 = 1 1 = 2 and dt2 dt 1 dt 1 dt 2 or v x1= v x 2 + v v x2 =v x1 − v and Similarly, Galilean acceleration Transformations: a2= a 1 Physics before Relativity Classical physics was developed between about 1650 and 1900 based on: * Idealized mechanical models that can be subjected to mathematical analysis and tested against observation.
    [Show full text]
  • Classical Mechanics
    Classical Mechanics Hyoungsoon Choi Spring, 2014 Contents 1 Introduction4 1.1 Kinematics and Kinetics . .5 1.2 Kinematics: Watching Wallace and Gromit ............6 1.3 Inertia and Inertial Frame . .8 2 Newton's Laws of Motion 10 2.1 The First Law: The Law of Inertia . 10 2.2 The Second Law: The Equation of Motion . 11 2.3 The Third Law: The Law of Action and Reaction . 12 3 Laws of Conservation 14 3.1 Conservation of Momentum . 14 3.2 Conservation of Angular Momentum . 15 3.3 Conservation of Energy . 17 3.3.1 Kinetic energy . 17 3.3.2 Potential energy . 18 3.3.3 Mechanical energy conservation . 19 4 Solving Equation of Motions 20 4.1 Force-Free Motion . 21 4.2 Constant Force Motion . 22 4.2.1 Constant force motion in one dimension . 22 4.2.2 Constant force motion in two dimensions . 23 4.3 Varying Force Motion . 25 4.3.1 Drag force . 25 4.3.2 Harmonic oscillator . 29 5 Lagrangian Mechanics 30 5.1 Configuration Space . 30 5.2 Lagrangian Equations of Motion . 32 5.3 Generalized Coordinates . 34 5.4 Lagrangian Mechanics . 36 5.5 D'Alembert's Principle . 37 5.6 Conjugate Variables . 39 1 CONTENTS 2 6 Hamiltonian Mechanics 40 6.1 Legendre Transformation: From Lagrangian to Hamiltonian . 40 6.2 Hamilton's Equations . 41 6.3 Configuration Space and Phase Space . 43 6.4 Hamiltonian and Energy . 45 7 Central Force Motion 47 7.1 Conservation Laws in Central Force Field . 47 7.2 The Path Equation .
    [Show full text]
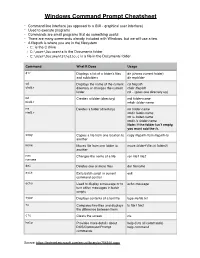
  • Windows Command Prompt Cheatsheet
    Windows Command Prompt Cheatsheet - Command line interface (as opposed to a GUI - graphical user interface) - Used to execute programs - Commands are small programs that do something useful - There are many commands already included with Windows, but we will use a few. - A filepath is where you are in the filesystem • C: is the C drive • C:\user\Documents is the Documents folder • C:\user\Documents\hello.c is a file in the Documents folder Command What it Does Usage dir Displays a list of a folder’s files dir (shows current folder) and subfolders dir myfolder cd Displays the name of the current cd filepath chdir directory or changes the current chdir filepath folder. cd .. (goes one directory up) md Creates a folder (directory) md folder-name mkdir mkdir folder-name rm Deletes a folder (directory) rm folder-name rmdir rmdir folder-name rm /s folder-name rmdir /s folder-name Note: if the folder isn’t empty, you must add the /s. copy Copies a file from one location to copy filepath-from filepath-to another move Moves file from one folder to move folder1\file.txt folder2\ another ren Changes the name of a file ren file1 file2 rename del Deletes one or more files del filename exit Exits batch script or current exit command control echo Used to display a message or to echo message turn off/on messages in batch scripts type Displays contents of a text file type myfile.txt fc Compares two files and displays fc file1 file2 the difference between them cls Clears the screen cls help Provides more details about help (lists all commands) DOS/Command Prompt help command commands Source: https://technet.microsoft.com/en-us/library/cc754340.aspx.
    [Show full text]
  • Creating Rpms Guide
    CREATING RPMS (Student version) v1.0 Featuring 36 pages of lecture and a 48 page lab exercise This docu m e n t serves two purpose s: 1. Representative sample to allow evaluation of our courseware manuals 2. Make available high quality RPM documentation to Linux administrators A bout this m aterial : The blue background you see simulates the custom paper that all Guru Labs course w are is printed on. This student version does not contain the instructor notes and teaching tips present in the instructor version. For more information on all the features of our unique layout, see: http://ww w . g urulabs.co m /courseware/course w are_layout.php For more freely available Guru Labs content (and the latest version of this file), see: http://www.gurulabs.co m/goodies/ This sample validated on: Red Hat Enterprise Linux 4 & Fedora Core v3 SUSE Linux Enterprise Server 9 & SUSE Linux Professional 9.2 About Guru Labs: Guru Labs is a Linux training company started in 199 9 by Linux experts to produce the best Linux training and course w are available. For a complete list, visit our website at: http://www.gurulabs.co m/ This work is copyrighted Guru Labs, L.C. 2005 and is licensed under the Creative Common s Attribution- NonCom mer cial- NoDerivs License. To view a copy of this license, visit http://creativecom m o n s.org/licenses/by- nc- nd/2.0/ or send a letter to Creative Commons, 559 Nathan Abbott Way, Stanford, California 943 0 5, USA. Guru Labs 801 N 500 W Ste 202 Bountiful, UT 84010 Ph: 801-298-5227 WWW.GURULABS.COM Objectives: • Understand
    [Show full text]
  • Influence of Angular Velocity of Pedaling on the Accuracy of The
    Research article 2018-04-10 - Rev08 Influence of Angular Velocity of Pedaling on the Accuracy of the Measurement of Cyclist Power Abstract Almost all cycling power meters currently available on the The miscalculation may be—even significantly—greater than we market are positioned on rotating parts of the bicycle (pedals, found in our study, for the following reasons: crank arms, spider, bottom bracket/hub) and, regardless of • the test was limited to only 5 cyclists: there is no technical and construction differences, all calculate power on doubt other cyclists may have styles of pedaling with the basis of two physical quantities: torque and angular velocity greater variations of angular velocity; (or rotational speed – cadence). Both these measures vary only 2 indoor trainer models were considered: other during the 360 degrees of each revolution. • models may produce greater errors; The torque / force value is usually measured many times during slopes greater than 5% (the only value tested) may each rotation, while the angular velocity variation is commonly • lead to less uniform rotations and consequently neglected, considering only its average value for each greater errors. revolution (cadence). It should be noted that the error observed in this analysis This, however, introduces an unpredictable error into the power occurs because to measure power the power meter considers calculation. To use the average value of angular velocity means the average angular velocity of each rotation. In power meters to consider each pedal revolution as perfectly smooth and that use this type of calculation, this error must therefore be uniform: but this type of pedal revolution does not exist in added to the accuracy stated by the manufacturer.
    [Show full text]
  • Basement Flood Mitigation
    1 Mitigation refers to measures taken now to reduce losses in the future. How can homeowners and renters protect themselves and their property from a devastating loss? 2 There are a range of possible causes for basement flooding and some potential remedies. Many of these low-cost options can be factored into a family’s budget and accomplished over the several months that precede storm season. 3 There are four ways water gets into your basement: Through the drainage system, known as the sump. Backing up through the sewer lines under the house. Seeping through cracks in the walls and floor. Through windows and doors, called overland flooding. 4 Gutters can play a huge role in keeping basements dry and foundations stable. Water damage caused by clogged gutters can be severe. Install gutters and downspouts. Repair them as the need arises. Keep them free of debris. 5 Channel and disperse water away from the home by lengthening the run of downspouts with rigid or flexible extensions. Prevent interior intrusion through windows and replace weather stripping as needed. 6 Many varieties of sturdy window well covers are available, simple to install and hinged for easy access. Wells should be constructed with gravel bottoms to promote drainage. Remove organic growth to permit sunlight and ventilation. 7 Berms and barriers can help water slope away from the home. The berm’s slope should be about 1 inch per foot and extend for at least 10 feet. It is important to note permits are required any time a homeowner alters the elevation of the property.
    [Show full text]
  • Two-Dimensional Rotational Kinematics Rigid Bodies
    Rigid Bodies A rigid body is an extended object in which the Two-Dimensional Rotational distance between any two points in the object is Kinematics constant in time. Springs or human bodies are non-rigid bodies. 8.01 W10D1 Rotation and Translation Recall: Translational Motion of of Rigid Body the Center of Mass Demonstration: Motion of a thrown baton • Total momentum of system of particles sys total pV= m cm • External force and acceleration of center of mass Translational motion: external force of gravity acts on center of mass sys totaldp totaldVcm total FAext==mm = cm Rotational Motion: object rotates about center of dt dt mass 1 Main Idea: Rotation of Rigid Two-Dimensional Rotation Body Torque produces angular acceleration about center of • Fixed axis rotation: mass Disc is rotating about axis τ total = I α passing through the cm cm cm center of the disc and is perpendicular to the I plane of the disc. cm is the moment of inertial about the center of mass • Plane of motion is fixed: α is the angular acceleration about center of mass cm For straight line motion, bicycle wheel rotates about fixed direction and center of mass is translating Rotational Kinematics Fixed Axis Rotation: Angular for Fixed Axis Rotation Velocity Angle variable θ A point like particle undergoing circular motion at a non-constant speed has SI unit: [rad] dθ ω ≡≡ω kkˆˆ (1)An angular velocity vector Angular velocity dt SI unit: −1 ⎣⎡rad⋅ s ⎦⎤ (2) an angular acceleration vector dθ Vector: ω ≡ Component dt dθ ω ≡ magnitude dt ω >+0, direction kˆ direction ω < 0, direction − kˆ 2 Fixed Axis Rotation: Angular Concept Question: Angular Acceleration Speed 2 ˆˆd θ Object A sits at the outer edge (rim) of a merry-go-round, and Angular acceleration: α ≡≡α kk2 object B sits halfway between the rim and the axis of rotation.
    [Show full text]